2022牛客蔚来杯加赛

M.Maimai DX 2077

• 题意

  • f四个操作都有五种等级分，一种操作有额外加分，问得分率

• 题解

  • 签到题

• 代码

#include 

using namespace std;

int main() {
    double stand[4][5]=//标准分
          {1,1,0.8,0.5,0,
           2,2,1.6,1.0,0,
           3,3,2.4,1.5,0,
           5,5,2.5,2,0};
    double extra[5]={1,0.5,0.4,0.3,0};//额外分
    
    double A=0,A0=0,B=0,B0=0,x;
    for(int i=0;i<4;i++)
        for(int j=0;j<5;j++) {
            cin>>ghaqx;
            A0+=stand[i][j]*x;//实际分
            A+=stand[i][0]*x;//满分
            if(i==3) {
                B0+=extra[j]*x;//额外实际分
                B+=extra[0]*x;//额外满分
            }
        }
    printf("%.9lf\n",A0/A*100+B0/B);//输出百分比(除去百分号)
    
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

E.Everyone is bot

• 题意

  • 共有n个人在复读，序号从小到大次序选择复不复读，只能复读一次
  • 若第i个人在这次复读当中排第j，那么他将获得a[i,j]瓶冰红茶
  • 若某人是所有复读中倒数第p个，那么罚154瓶冰红茶(血亏)
  • 每个人想自己的冰红茶数量尽可能多，请输出n个人的冰红茶数量

• 题解

  • 谁都不愿意当倒数第p个，所以当复读人数到达第p个时，不会有人复读；而所有在倒数p之前可以选择复读的人一定会选择复读
  • 所以只有前n%p个人选择复读，拿到的是a[i,i]瓶冰红茶，后面的人都没有冰红茶

• 代码

#include 

using namespace std;
const int N=1010;

int n,p,a[N][N];

int main() {
    cin>>n>>p;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            cin>>a[i][j];
    
    for(int i=1;i<=n;i++)
        if(i>(n%p)) cout<<"0 ";
        else cout<<a[i][i]<<" ";

    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

H.Here is an Easy Problem of Zero-chan

• 题意

  • n个点的以1为根树
  • 询问q次，每次给定一个节点编号x，问树中所有点与x的lca之积有多少个后缀0

• 题解

  • 后缀0可以简化为找有多少个2和5的因子，2,5因子数量少的数量即为后缀0的个数
  • 归于每次询问，暴力枚举两两点算出乘积复杂度暴了，所以优化。因为是算lca，观察可得，对于u节点，以u为根的子树下的点与u的lca就是u本身，而u之外的点与u的lca为u的父节点。即发现每个点与父节点相关，所以考虑树形dp
  • 观察，假设f2[u]为询问u时所有lca的乘积中2的因子数量，cnt2[u]为u的2的因子数量，sz[u]为以u为根的子树的大小。下图中以u=1为例，所有点与1的lca都相同为1，所以f2[u]=cnt2[u]*sz[u]。当转移到点2时，即u=2时，2的子树下点与2的lca变为2，其他点与2的lca不变依然为1，所以有转移方程为f2[u]=f2[fa]-sz[u]*cnt2[fa]+sz[u]*cnt2[u]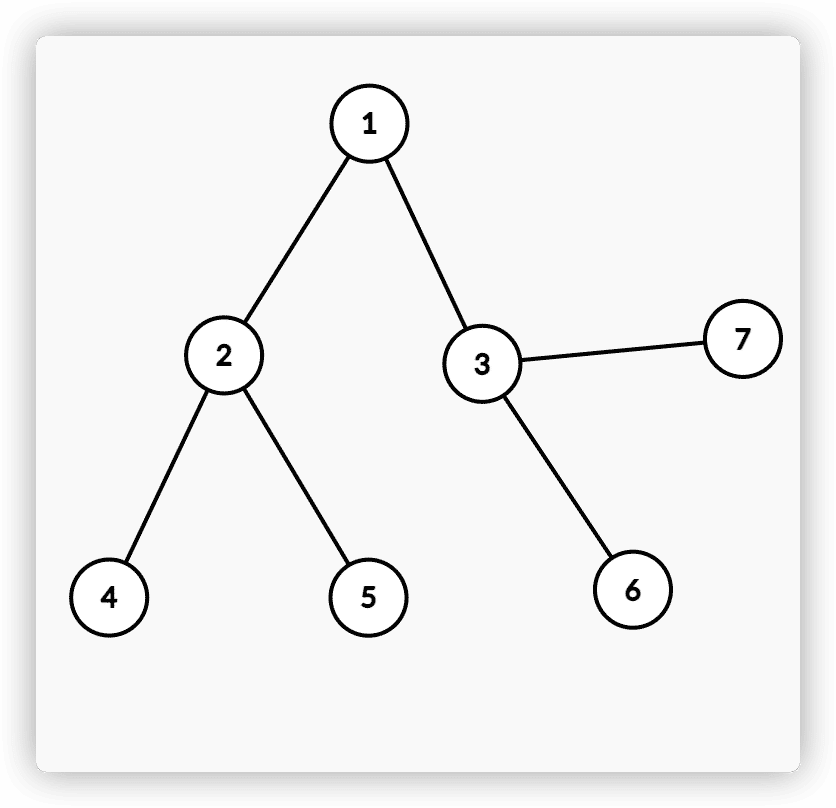
  • 由于有sz,cnt等数据需要在转移前处理，所以先dfs预处理这几个数据，之后在dfs进行树形dp的转移

• 代码

#include 
#include 

using namespace std;
const int N=1e5+10;

int n,q;
int h[N],e[2*N],ne[2*N],idx;//建树
int f2[N],f5[N],cnt2[N],cnt5[N],sz[N];//状态，因子数，子树大小

void add(int a,int b) {//加边
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}

int get(int x,int cot) {//计算x中cot的因子数量
    int res=0;
    while(x%cot==0) {
        res++;
        x/=cot;
    }
    return res;
}

void dfs(int u,int fa) {//dfs树预处理sz数组以及cnt数组
    sz[u]=1;
    cnt2[u]=get(u,2);
    cnt5[u]=get(u,5);
    for(int i=h[u];~i;i=ne[i]) {
        int v=e[i];
        if(v==fa) continue;
        dfs(v,u);
        sz[u]+=sz[v];
    }
}

void dfs1(int u,int fa) {//树形dp转移
    f2[u]=f2[fa]+(cnt2[u]-cnt2[fa])*sz[u];
    f5[u]=f5[fa]+(cnt5[u]-cnt5[fa])*sz[u];
    for(int i=h[u];~i;i=ne[i]) {
        int v=e[i];
        if(v==fa) continue;
        dfs1(v,u);
    }
}

int main() {
    cin.tie(0)->sync_with_stdio(false);
    cin>>n>>q;
    
    int u,v;
    memset(h,-1,sizeof h);//初始化
    for(int i=1;i<n;i++) {
        cin>>u>>v;
        add(u,v);add(v,u);
    }
    
    dfs(1,0);
    dfs1(1,0);//预处理好因子数量
    while(q--) {
        int x;
        cin>>x;
        cout<<min(f2[x],f5[x])<<'\n';//直接输出
    }
    
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66

J.Jellyfish and its dream

• 题意

  • 给一个长度为n的只含有012的环
  • 若某一位+1在mod 3意义下等于其后一位，那么此位置变成后一位数
  • 问所有位置能否变成一样

• 题解

  • 一般序列变化为邻位加法时，考虑差分

    令差分序列b[i]=(a[(i+1)%3]-a[i]+3)%3
    对于(2,1)这种差分，比如2 1 2,可以改变中间数字变成(0,0)
    对于(1,1)这种差分，比如0 1 2,可以改变中间数字变成(2,0)
    对于(0,1)这种差分，比如0 0 1,可以改变中间数字变成(1,0)
    对于(1,0)这种差分，比如0 1 1,可以改变首位数字变成(0,0)
    
    故可以发现几个性质：
    (2,1),(1,0)这两种差分可以直接变成(0,0)
    (0,1)可以转化为(1,0)，实现了1的移动
    (1,1)可以转化为(2,0)，实现1->2转换
    
    目标为:把所有数字变成一样，所以差分数组应该全变为0
    差分序列中的1可以有两种方式变为0，一个是直接(1,0)变为0，另一个是(1,1)->(2,0)+(1,0)->(0,1)=(2,1)->(0,0)
    差分序列中的2必须由后一位1变成0，即(2,0)+(0,1)->(1,0)=(0,0)
    
    所以得出结论:差分序列中必须要有足够的1把2消除，其余多的1没关系可以直接变0
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16

  • 因此，只要差分序列中的1个数不小于2的即可

• 代码

#include 
#include 
using namespace std;

int main() {
    int t,n;
    cin>>t;
    while(t--) {
        cin>>n;
        vector<int> a(n);
        for(int i=0;i<n;i++) cin>>a[i];
        
        int cnt=0;//记录序列中1，2的个数
        for(int i=0;i<n;i++) 
            if((a[(i+1)%n]-a[i]+3)%3==1) cnt++;
            else if((a[(i+1)%n]-a[i]+3)%3==2) cnt--;
        cout<<(cnt<0 ? "No":"Yes")<<'\n';
    }
    
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21