-
论文精读:GHM:Gradient Harmonized Single-stage Detector
Abstract
尽管两级探测器取得了巨大的成功,但单级探测器仍然是一种更加优雅和有效的方法,但在训练过程中存在两种众所周知的不和谐,即正负例子和硬性例子在数量上的巨大差异。在这项工作中,我们首先指出,这两个不协调的本质影响可以用梯度来总结。此外,我们提出了一种新的梯度协调机制(GHM)来作为不协调的对冲。GHM背后的原理可以很容易地嵌入到交叉熵等类损失函数(CE)和回归损失函数如smooth-L1(SL1)损失中。为此,设计了两种新的损失函数GHM-C和GHM-R,分别用来平衡梯度流进行锚定分类和边界框细化。对MS COCO的消融研究表明,如果不进行费力的超参数调整,GHM-C和GHM-R都可以为单级探测器带来实质性的改进。在没有任何whistles和bells的情况下,所提出的模型在COCO测试集上达到了41.6 mAP,超过了最先进的方法
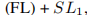 0.8 AP
0.8 AP1.Introduction
一步级方法是最有效和最优雅的目标检测框架。但长期以来,单级探测器的性能与两级探测器有较大的差距。单阶段检测器训练中最具挑战性的问题是容易例子和难例子之间以及正例子和负例子之间的严重不平衡。大量的简单的和有背景的例子往往会压倒训练。但由于方案驱动的机制,两级探测器并不存在这些问题。为了处理前一个不平衡问题,通常使用基于挖掘的方法,如OHEM,但它们直接放弃了大多数例子,训练效率低下。对于后一种不平衡,最近的工作,焦点损失(Linetal.2017b),试图通过将交叉熵损失函数修正为一个精心设计的形式来解决这个问题。然而,焦点损失采用了两个超参数,需要大量的努力来调整。这是一种静态损失,不适应数据分布的变化,随着训练过程的变化而变化。
本文首先指出,阶级的不平衡可以概括为困难的不平衡,困难的不平衡可以概括为梯度范数分布的不平衡。如果一个积极的例子被很好地分类,那么它就是一个简单的例子,并且模型从中受益甚少,也就是说,这个样本将产生少量的梯度。而一个错误分类的例子,无论模型属于哪个类别,都应该引起模型的注意。所以如果从全局来看,大量的负的例子往往很容易分类,而难的例子通常是正的。所以这两种不平衡可以大致概括为属性不平衡。
此外,我们认为具有不同属性的梯度范数的分布可以暗示具有不同属性的实例(硬/容易和正样本/负样本)的不平衡。例子的密度为w.r.t.梯度范数,我们称为方便的梯度密度,变化很大,如图1左侧所示。梯度范数很小的例子具有相当大的密度,这与大量容易出现的负例子相对应。虽然一个简单的例子对全局梯度的贡献不如一个困难的例子,但大量简单的例子的总贡献可能会超过少数硬例子的贡献,而且训练过程将是低效的。此外,我们还发现具有非常大梯度范数(非常困难的例子)的密度略大于介质例子的密度。我们认为这些非常困难的例子大多是异常值,因为即使模型收敛,它们也稳定存在。异常值可能会影响模型的稳定性,因为它们的梯度可能与其他常见的例子有很大的差异。
受梯度范数分布分析的启发,我们提出了一种梯度协调机制(GHM)来有效地训练一期目标检测模型,重点研究了不同实例的梯度贡献的和谐性。GHM首先对具有相似属性w.r.t的梯度密度的例子的数量进行统计,然后根据密度对每个例子的梯度附加一个协调参数。GHM与CE和FL相比的效果如图1右侧所示。使用GHM进行训练,简单例子产生的大量累积梯度可以很大程度上降低,异常值也可以相对降低。最后,每种例子的贡献将得到平衡,训练可以更加有效和稳定。
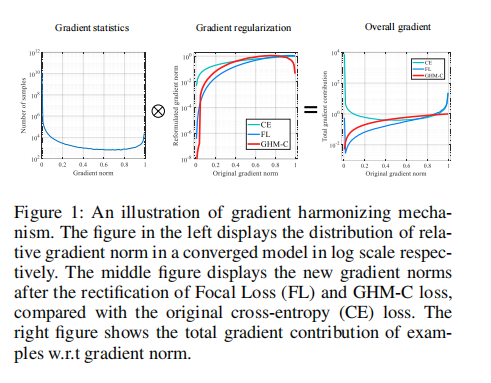
在实际应用中,梯度的修改可以通过重新构造损失函数来等价地实现,我们将GHM嵌入到分类损失中,记为GHM-c损失。这个损失函数的公式很优雅,没有许多超参数来调整。由于梯度密度是一个统计变量,取决于一个小批中的样本分布,GHM-C是一个动态损失,可以适应每个批中数据分布的变化以及模型的更新。为了展示GHM的通用性,我们也在预测框回归分支中采用它作为GHM-r损失的形式。
对具有挑战性的COCO基准的边界框检测轨道的实验表明,与传统的交叉熵损失相比,GHM-C损失具有较大的增益,略高于最先进的焦点损失。而GHM-R损失的性能也优于常用的smooth L1 损失。GHMC和GHM-R的组合在COCO技术开发集上获得了一个新的最先进的性能。
我们的主要贡献如下:
1.我们揭示了在梯度范数分布中,单级检测器的重要实例不平衡背后的基本原理,并提出了一种新的梯度协调机制(GHM)来处理它。
2.我们将GHM分别作为GHM-C和GHM-R嵌入到分类和回归的损失中,它修正了具有不同属性的例子的梯度贡献,并对超参数具有鲁棒性。
3.与GHM合作,我们可以轻松地训练一个单级检测器,并在COCO基准测试上实现最先进的结果。
2.Related Work
Object Detection: 目标检测是计算机视觉领域中最基本、最重要的任务之一。基于深度卷积神经网络(CNN)的方法,如(Ren等,2015;刘等,2016;雷蒙和法哈迪,2017;他等,2017),近年来,由于(西蒙扬和齐塞曼,2014;Szegedy等,2016;他等,2016;黄等,2017)。先进的目标检测框架可分为一级探测器和两级探测器两类。
大多数最先进的方法采用两级探测器,例如(Girshick2015;任等2015;李等2017;他等2017;林等2017a;Zeng等2018)。它们主要是基于区域CNN(R-CNN)的体系结构。这些方法首先从几乎无限的候选区域中获得可管理的数量的称为感兴趣区域(RoI)的区域建议,然后使用网络来评估每个RoI。
单级探测器具有结构简单、速度快的优点。SSD(Liu等人2016;傅等人2017)、YOLO(雷蒙等人2016;雷蒙和法哈迪2017;雷蒙和法哈迪2018)用于通用目标检测和RSA(Sog等人;刘等人2017)用于人脸检测已经实现了良好的速度/精度权衡。然而,它们的精度很难超过两级探测器。RetinaNet(Lin et al.2017b)是最先进的单级目标探测器,其性能与双级探测器相当。它采用了RPN(Ren et al.2015)改进的架构,重点解决训练过程中的类别不平衡。
Object Functions for Object Detector: 大多数检测模型采用基于交叉熵的损失函数进行分类(Girshick2015;Ren等2015;刘等2016;Dai等2016;Lin等2017a;He等2017)。而同步探测器则面临着两级探测器所不存在的极端类不平衡的问题。早期的方法试图使用硬的例子挖掘方法,例如(斯里瓦斯塔瓦、古普塔和吉希克2016;费尔森斯瓦尔布、吉希克和麦卡莱斯特2010),但他们放弃了大多数例子,不能很好地处理这个问题。最近的这项工作(Lin et al.2017b)重新制定了交叉熵损失,使容易的负样本被减少,而困难的例子不受影响,甚至增加。
为了稳定地进行预测框回归的训练,Fast R-CNN(Girshick 2015)引入了smooth L1损失。这种损失减少了异常值的影响,从而使模型的训练更加稳定。以下几乎所有工作都将smooth L1损失作为边界框回归的默认值(Ren等2015;Liu等2016;Dai等2016;Lin等2017a;He等2017)。
这项工作(Imani和White 2018)试图通过将目标改变为一个分布和使用直方图损失来计算预测和目标的K-L散度来提高回归性能。该工作(Chen et al.2017)通过动态调整不同任务分支的梯度幅度来平衡多任务损失。
我们基于GHM的损失根据其梯度的分布来协调了实例的贡献,从而可以很好地处理类的不平衡和异常值问题。它还可以使权重适应每个小批中数据分布的变化。
Gradient Harmonizing Mechanism Problem Description
类似于(Linetal.2017b),我们在这里的工作集中在单阶段对象检测的分类,其中示例的类(前景/背景)是相当不平衡的。对于一个候选框,设p∈[0,1]为模型预测的概率,p∗∈{0,1}为某一类的基本真值标签。考虑二进制交叉熵损失:
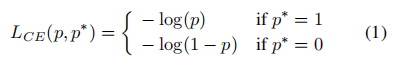
设x是模型的直接输出,这样p=sigmoid(x),我们有关于x的梯度:
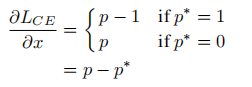
我们对g的定义如下:
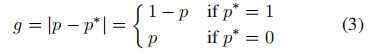
g等于梯度w.r.t x的范数。g的值表示一个示例的属性(例如,简单的或硬的),并暗示了该示例对全局梯度的影响。虽然梯度的严格定义是在整个参数空间上的,这意味着g是一个例子的梯度的相对范数,但为了方便起见,在本文中我们称g为梯度范数。
图2显示了收敛的年龄检测模型中g的分布。由于简单的否定有一个主导数字,我们使用对数轴来显示示例的分数,以演示具有不同属性的示例的方差的细节。可以看出,非常简单的例子的数量非常大,这对全球梯度有很大的影响。此外,我们可以看到,一个收敛的模型仍然不能处理一些非常困难的例子,其数量甚至大于中等困难的例子。这些非常困难的例子可以看作是离群值,因为它们的梯度方向往往在很大程度上与其他大量的例子的梯度方向变化。也就是说,如果收敛模型被迫学习更好地对这些异常值进行分类,那么对大量其他例子的分类往往会不那么准确。
Gradient Density
为了解决梯度范数分布的不协调问题,我们引入了一种关于梯度密度的协调方法。将训练实例的梯度密度函数设为等式。
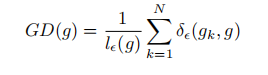
其中gk是第k个例子的梯度范数。并且:
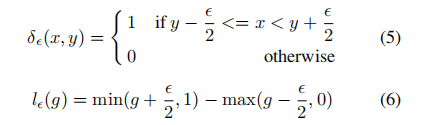
g的梯度密度表示以g为中心,长度为
 ,并由该区域的有效长度归一化。
,并由该区域的有效长度归一化。现在我们将梯度密度协调参数定义为:

其中,N为示例的总数。为了更好地理解梯度密度协调参数,我们可以将其改写为
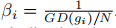 。分母
。分母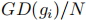 是一个归一化器,表示具有邻域梯度的例子的比例。如果这些例子在梯度上均匀分布,那么任何gi的GD(gi)=N和每个例子都有相同的βi=1,这意味着没有任何改变。否则,密度较大的例子将被归一化器相对降低权重。
是一个归一化器,表示具有邻域梯度的例子的比例。如果这些例子在梯度上均匀分布,那么任何gi的GD(gi)=N和每个例子都有相同的βi=1,这意味着没有任何改变。否则,密度较大的例子将被归一化器相对降低权重。 GHM-C Loss
我们将βi作为第i个例子的损失权重,将GHM嵌入到分类损失中,损失函数的梯度密度协调形式为:
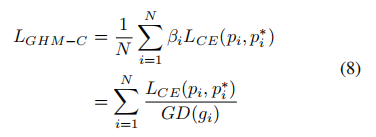
图3显示了不同损失的重新制定的梯度范数。这里我们以CE的原始梯度范数,即g=|p−p∗|,作为x轴,以获得方便的视图,因为密度是根据g计算的。我们可以看到,焦点损失和GHM-C损失的曲线有相似的趋势,这意味着具有最佳超参数的焦点损失与均匀梯度协调是相似的。此外,GHM-C还有一个焦点损失忽略的优点:降低离群值的梯度贡献。
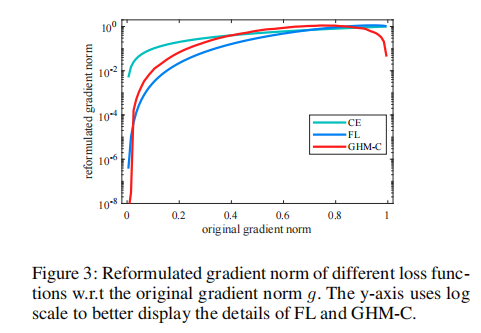
由于我们的GHM-C损失,大量非常简单的例子在很大程度上被降低了加权,异常值也被略微降低了加权,这同时解决了属性不平衡问题和异常值问题。从图1的右图中,我们可以更好地看到,GHM-C协调了不同例子组的总梯度贡献。由于每次迭代都计算梯度密度,所以例子的权重不是固定的w.r.t.G(或x)像焦点损失,但自适应当前的模型状态和小批量数据。GHM-C损失的动态特性使训练更加有效和鲁棒性。
Unit Region Approximation
Complexity Analysis: 计算所有例子的梯度密度值的朴素算法的时间复杂度为O(
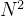 ),可以很容易地从方程4和8中得到。即使并行计算,每个计算单元仍然承担计算N。据我们所知,最好的算法首先通过对梯度范数排序的复杂性
),可以很容易地从方程4和8中得到。即使并行计算,每个计算单元仍然承担计算N。据我们所知,最好的算法首先通过对梯度范数排序的复杂性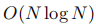 ,然后使用一个队列扫描的例子,得到他们的密度与O(N)。这种基于排序的方法并不能从并行计算中获得太多收益。由于单级探测器中的图像的N可以是105甚至106,因此直接计算梯度密度是相当耗时的。因此,我们引入了另一种方法来近似地获得实例的梯度密度。
,然后使用一个队列扫描的例子,得到他们的密度与O(N)。这种基于排序的方法并不能从并行计算中获得太多收益。由于单级探测器中的图像的N可以是105甚至106,因此直接计算梯度密度是相当耗时的。因此,我们引入了另一种方法来近似地获得实例的梯度密度。Unit Region: 我们将g的范围空间划分为长度为
 ,的单个单位区域,并有
,的单个单位区域,并有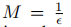 单位区域。设
单位区域。设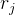 为索引j的单位区域,使
为索引j的单位区域,使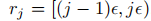 。设
。设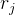 表示位于
表示位于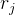 中的实例数。我们定义
中的实例数。我们定义 ,它是g所在的单位区域的索引函数。
,它是g所在的单位区域的索引函数。 然后,我们将近似的梯度密度函数定义为:
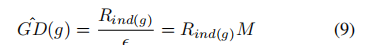
然后得到近似梯度密度协调参数:
考虑一下
 =1的特殊情况:只有一个单元区域,所有的例子都在其中,所以显然每个βi=1和每个例子都保持了它们原来的梯度贡献。最后,我们得到了重新表述的损失函数:
=1的特殊情况:只有一个单元区域,所有的例子都在其中,所以显然每个βi=1和每个例子都保持了它们原来的梯度贡献。最后,我们得到了重新表述的损失函数: 
从公式9我们可以看到,位于同一单位区域的例子具有相同的梯度密度。因此,我们可以使用直方图统计算法,计算所有梯度密度值的时间复杂度为O(MN)。并且并行计算可以使每个计算单元的计算量为m。在实际应用中,我们可以在相当少的单元区域内获得良好的性能。也就是说,M相当小,损失的计算是有效的。
EMA: 基于小批量统计的方法通常面临一个问题:当许多极端数据只是在一个小批量中采样时,统计结果会产生严重的噪声,训练会不稳定。指数移动平均线(EMA)是解决这一问题的一种常用方法,例如,带有动量的SGD(Sutskeveretal.2013年)和批处理归一化(Ioffe和Szegedy2015年)。由于在近似算法中,梯度密度来自于单元区域内的实例数,因此我们可以对每个单元区域应用EMA,以获得更稳定的实例梯度密度。设
 为第t次迭代中第j个单元区域的例子数,
为第t次迭代中第j个单元区域的例子数, 为移动平均数。我们有:
为移动平均数。我们有:
其中,α为动量参数。我们使用平均数Sj来计算梯度密度,而不是Rj:
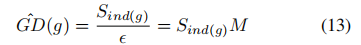
使用EMA,梯度密度将更加平滑,对极端数据不敏感。
GHM-R损失
考虑参数化偏移量
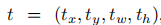 ,由盒子回归分支预测,目标偏移量
,由盒子回归分支预测,目标偏移量 ,从地面真相计算。回归损失通常采用平滑的L1损失函数:
,从地面真相计算。回归损失通常采用平滑的L1损失函数: 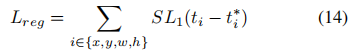
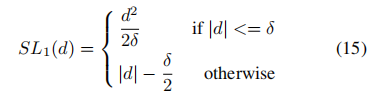
其中,δ是二次部分和线性部分之间的分法点,在实际应用中通常设为1/9。
由于
 ,smooth L1损失关于
,smooth L1损失关于的梯度可以表示为:
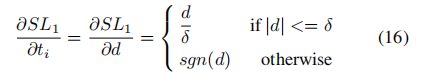
其中sgn是sign函数。
请注意,所有|d|大于分割点的示例都具有相同的梯度范数
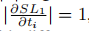 ,这使得如果依赖于梯度范数,则无法区分具有不同属性的范例。另一种选择是直接使用|d|作为不同属性的测量,但新的问题是|d|在理论上可以达到无限,单位区域不能实现近似。
,这使得如果依赖于梯度范数,则无法区分具有不同属性的范例。另一种选择是直接使用|d|作为不同属性的测量,但新的问题是|d|在理论上可以达到无限,单位区域不能实现近似。为了方便地将GHM应用于回归损失,我们首先将传统的SL1损失修改为一个更优雅的形式:
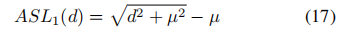
这个损失与SL1损失具有相似的性质:当d很小时,它近似于一个二次函数(L2损失),而当d很大时,它近似于一个线性函数(L1损失)。我们将修正后的损失函数表示为Authentic Smooth L1(ASL1)损失,这意味着所有的导数度都是存在且连续的。相比之下,Smooth L1损失的二阶导数在d=δ点不存在。此外,ASL1损失有一个优雅的关于d的梯度形式:
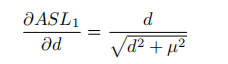
梯度的范围只有[0,1),因此回归中ASL1损失的单位区域密度的计算与分类中的CE损失一样方便。在实践中,我们将ASL1损失的µ=设置为0.02,以保持与SL1损失相同的性能。
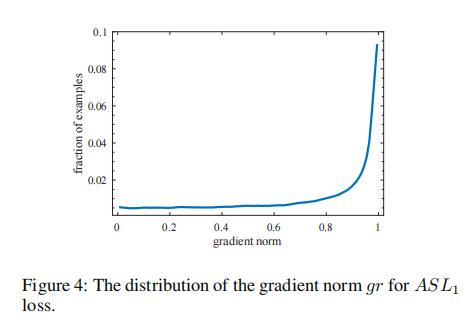
我们将
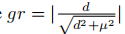 定义为ASL1损失的梯度范数,收敛模型的梯度分布如图4所示。我们可以看到有大量的异常值。请注意,回归只对积极的例子进行,因此对于分类和回归之间的不同分布趋势是合理的。最重要的是,我们可以将GHM应用于回归损失:
定义为ASL1损失的梯度范数,收敛模型的梯度分布如图4所示。我们可以看到有大量的异常值。请注意,回归只对积极的例子进行,因此对于分类和回归之间的不同分布趋势是合理的。最重要的是,我们可以将GHM应用于回归损失: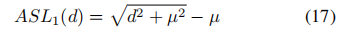

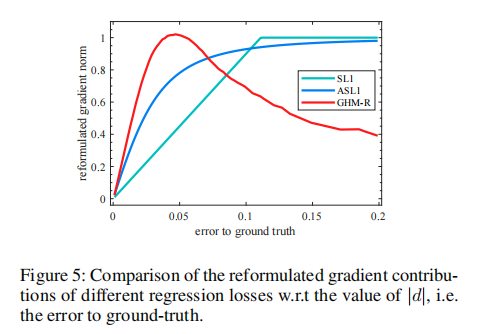
图5中SL1损失、ASL1损失和GHM-R损失的重新制定的梯度贡献。x轴采用|d|,便于比较。
我们强调,在预测框回归中,并不是所有的“简单的例子”都不重要。分类中一个简单的例子通常是一个预测概率很低的背景区域,并且肯定会被排除在最终的候选区域之外。因此,对这类例子的改进对精度几乎没有贡献。但在预测框回归中,一个简单的例子仍然偏离了地面的真实位置。更好的预测任何实例将直接提高最终候选框的质量。此外,先进的数据集更关注定位精度。例如,COCO(Lin et al.2014)将IoU阈值0.5到0.95的平均AP作为评估算法的度量。在这个度量中,一些所谓的简单示例(那些有小误差的)也很重要,因为减少它们的误差可以直接提高高阈值下的AP(例如AP@IoU=0.75)。
我们的GHM-R损失可以通过向上加权简单例子的重要部分和降低加权异常值来协调简单和硬例子对box回归的贡献。实验结果表明,该方法的实验性能优于SL1和ASL1。
Experiments
我们在具有挑战性的COCO基准上评估了我们的方法(Linetal.2014)。对于培训,我们遵循常用的实践(He等人,2017;Lin等人,2017b),将40k验证集分为35k子集和5k子集。将35k验证子集与整个80k训练集的并集一起用于训练,并表示为35k训练集。5k验证子集表示为小集,我们对其进行了消融研究。而我们的主要结果是在测试开发集上报告的。
Implementation Details
Network Setting: 我们使用RetinaNet(Lin等人2017b)作为网络架构,所有实验都采用ResNet(He等人2016)作为骨干,具有特征金字塔网络(FPN)(Lin等人2017a)结构。锚定使用3个尺度和3个高宽比来方便地与焦点损失进行比较。所有实验的输入图像比例均设置为800像素。对于所有的消融研究,均使用ResNet-50。而在测试开发上评估的动态模型采用了ResNeXt-101(Hu,Shen,和Sun2017)。与焦点损失相比,我们的方法不需要专门的偏置初始化。
Optimization:所有模型均采用常用的SGD算法进行优化。我们在8个GPU上训练模型,每个GPU上有2张图像,这样有效的小批量大小为16。所有的模型都被训练了14个时期,初始学习率为0.01,在第9阶段和第12阶段的初始学习率分别降低了0.1倍。我们还使用了一个权重衰减参数为0.0001和一个动量参数为0.9。唯一的数据增强操作是水平图像翻转。对于梯度密度计算中使用的EMA,我们对所有实验都使用α=0.75,因为结果对α的精确值不敏感。
GHM-C损失
为了关注GHM-C损失函数的影响,本节实验均采用平滑的L1损失函数,δ=1/9作为盒子回归分支。
Baseline: 我们以标准交叉熵损失为基线训练了一个模型。标准初始化会导致快速发散,因此我们遵循焦点损失(Lin et al.2017b),使用π=0.01将最后一层的偏差项初始化为b=−log((1−π)/π),以避免发散。但是在专门的初始化中,分类损失非常小,所以我们将分类损失增加了20,使求损失值合理(现在求分类损失值约为1)。但当模型收敛时,分类损失仍然很小,我们最终得到了一个平均精度(AP)为28.6的模型。
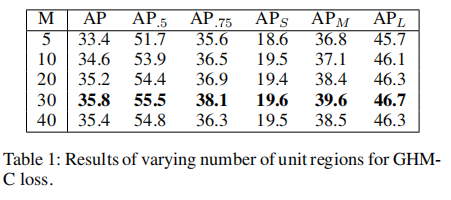
Number of Unit Region 表1表示变化M的结果,M是单位区域的数量。这里不适用EMA。当M太小时,密度在不同的梯度范数上不能有很好的变化,性能也不是很好。所以当M增加时,当M不大时,我们可以得到更多。然而,M并不一定很大,当M=30时,GHM-C损失比基线有足够大的改善。
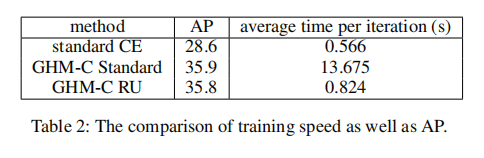
Speed: 由于我们的方法是一个损失函数,所以它不会改变推理的时间。对于训练,小M为30就足以获得良好的性能,所以梯度密度计算消耗的时间不长。表2表示训练过程中每次迭代的平均时间和平均精度。这里的“GHM-C Standard”是使用梯度密度的原始定义来实现的,“GHMC RU”表示区域单元逼近算法的实现。实验在1080个Ti gpu上进行。我们可以看到,我们的区域单元近似算法加快了训练的速度,而对性能的危害可以忽略不计。而与CE相比,GHM-C损失的减缓也是可以接受的。由于我们的损失现在还没有完全实现GPU,仍然有改进的空间。
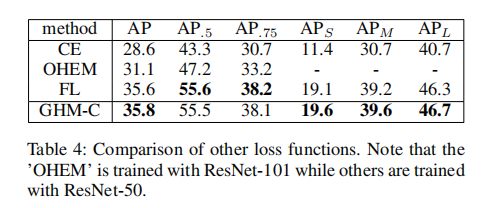
Comparison with Other Methods: 表4显示了使用我们的损失与其他损失函数或抽样策略相比的结果。由于使用焦点损失的微小模型的报告结果是用600像素的输入图像尺度进行训练的,为了公平比较,我们使用800像素的尺度重新训练了焦点损失,并保持了焦点损失的最佳参数。我们可以看到我们的损失比焦点损失稍微好一些。
GHM-R Loss
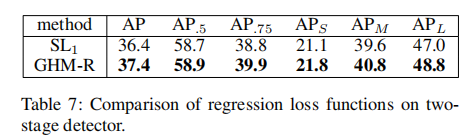
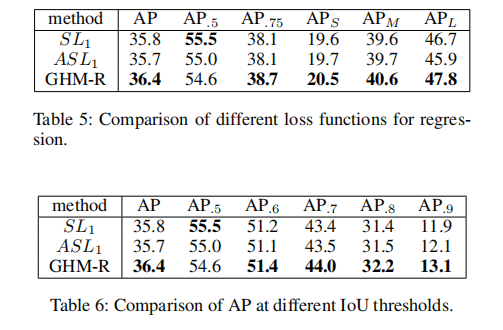
Comparison with Other Losses: 本实验对分类分支采用了GHM-C损失的最佳构型。因此,第一个基线是模型(使用SL1损失进行训练),在GHM-C损失实验中显示的AP为35.8。我们采用µ=0.02处理ASL1损失,以获得与SL1损失可比的结果,并获得GHM-R损失的公平基线。表5为基线SL1和ASL1损失以及GHM-R损失的结果。根据ASL1的损失,我们可以看到增加了0.7 mAP。表6显示了不同IoU阈值下的AP细节。GHM-R损失略微降低了AP@IoU=0.5,但当阈值更高时就会增加,这证明了我们的命题,即所谓的简单的回归例子对于精确定位是重要的。

Two-Stage Detector: 回归的GHM-R损失并不局限于单级检测器。因此,我们做了实验来验证对两级探测器的效果。我们的基线方法是Faster-RCNN与Res50-FPN模型,使用SL1损失进行预测框回归。表7表明,GHM-R损耗分别适用于两级探测器和一级探测器。
Main Results
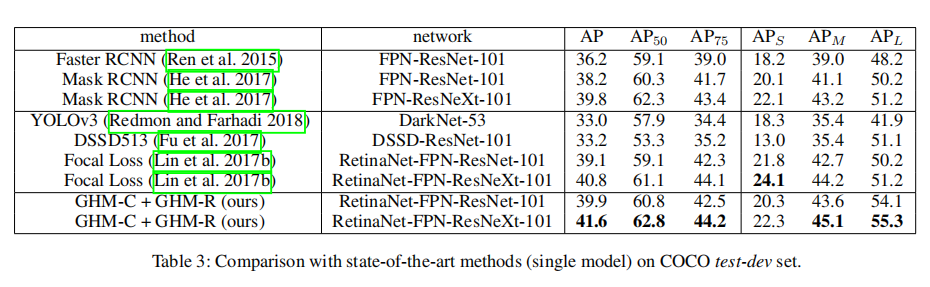
我们使用32x8d的FPN-ResNext101主干和RetinaNet模型,使用GHM-C损失进行分类,使用GHMR损失进行盒子回归。实验在测试开发集上进行了实验。表3显示了我们与最先进的方法相比的主要结果。我们的方法取得了优异的性能,并在大多数指标上优于焦点损失。
Conclusion and Discussion
在本文中,我们关注了单级探测器中的两个不平衡问题,并将这两个问题总结为样品差异中梯度密度的不协调。提出了两个损失函数GHM-C和GHMR来克服分类和边界框回归中的不和谐。实验表明,与GHM合作,单级探测器的性能可以轻松超越现代先进的FPN和Mask-RCNN。
尽管选择均匀分布作为目标有所改进,但我们仍然认为梯度的最优分布难以确定,需要进一步研究。
-
相关阅读:
Docker 的基本概念
【超简单-Java设计模式2】简单工厂模式
OpenShift集群规划
Java Collections.fill()方法具有什么功能呢?
2022-32周 项目问题整理
用python整个活(4)——哥德巴赫猜想
java-php-python-ssm郑工社团交流服务信息平台计算机毕业设计
用 AWTK 和 AWPLC 快速开发嵌入式应用程序 (4)- 自定义功能块(上)
改造 Kubernetes 自定义调度器
javascript的AMD模式
- 原文地址:https://blog.csdn.net/qq_52053775/article/details/126499085