傅里叶变换原理

傅里叶级数是将一个周期函数（非周期函数可以视为周期为无穷）拆分成无数的频率与幅度不同的简单sin函数的方法，这个方法对于任意的时域函数都适用，大家可以在这里查看形象的分解。
最直观的函数在工程上都是时域函数。所谓时域，即值随时间变化的函数。举一个简单例子，对于一个普通的sin函数，其时域表达是这样的：

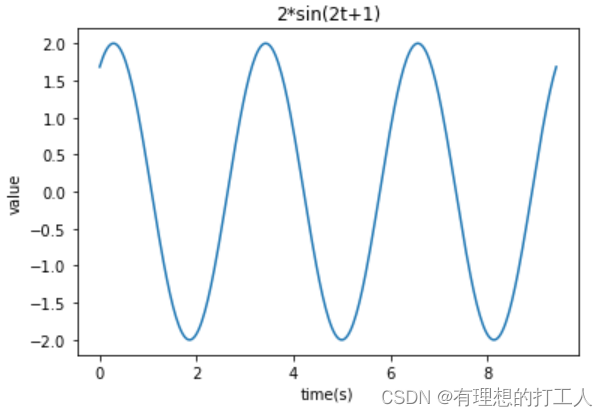
而在频域中，它的表达是这样的：

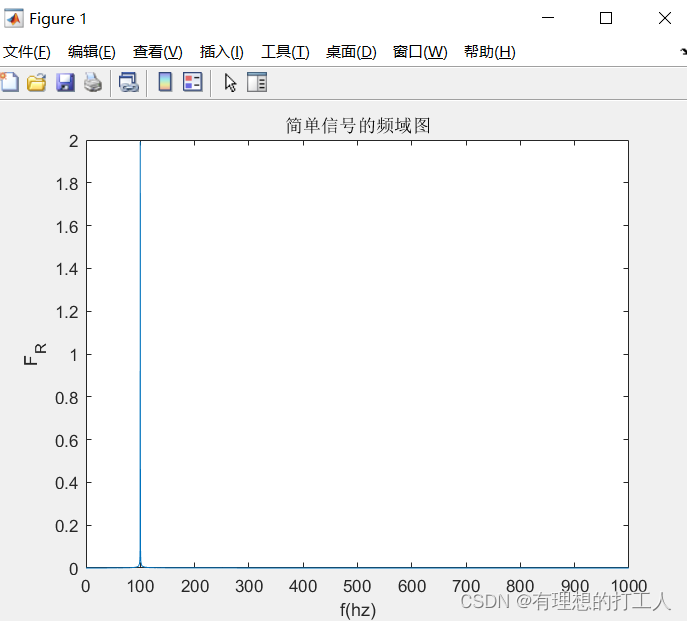
也就是说，频域分析抛弃了时间轴，而是选择频率（f）作为横轴，幅度（A）作为纵轴来分析函数。因为复杂的时域函数都是多个简单sin函数合成的，所以其频域表达就会是类似这样的：

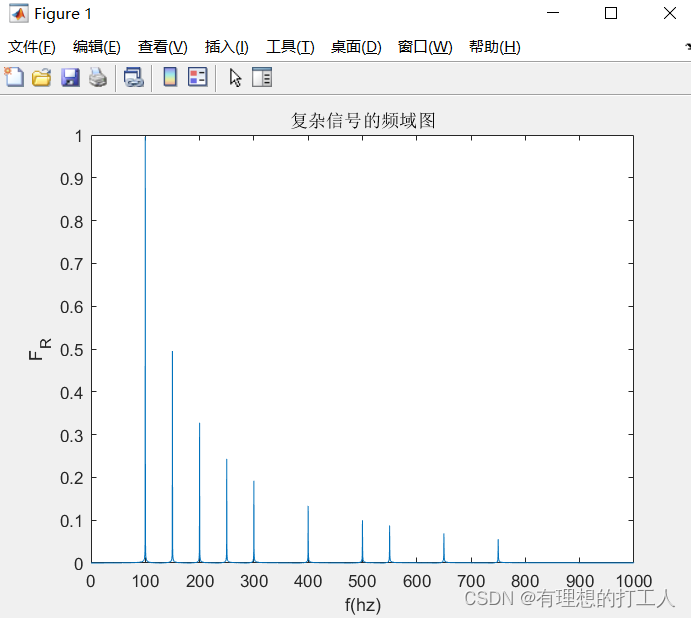
当然，我们的频域图没有办法表达全部的sin函数信息，比如这张图上没有相位（φ）的信息，也就是说我们还需要另一幅图像对φ加以表达。借用一位知乎网友的图来解释频域和时域的关系：

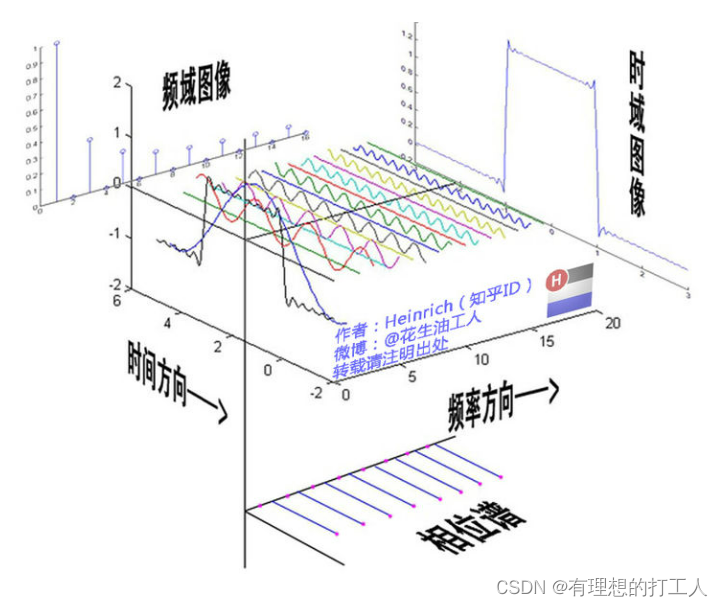
需要详细了解的小伙伴可以从这里查看大佬的解读。

傅里叶变换的应用

从傅里叶变换的公式中可以看出，越是高频的分量，其幅度越低，这个特点在连续域和离散域都是成立的。图像是一个离散域，以某一个像素点为参考，他周围八个方向有八个不同的像素值，某个方向相邻的像素值差距较大，就代表了这个方向的频率高，反之就是这个方向的频率低。从之前的学习之中不难理解，频率高的部分是图像的边界，也即图像的细节，反过来，频率低的地方细节信息就少。如果我们把一副普通图像转换成频率图，就可以根据频率的高低重新构建一张图像。这张图片之中，高频分量与高频分量聚集，低频分量与低频分量聚集。如果我们使用掩码盖住某个高频点所在的区域，就会一口气挡住相当多的细节信息，这就是低通滤波的原理。
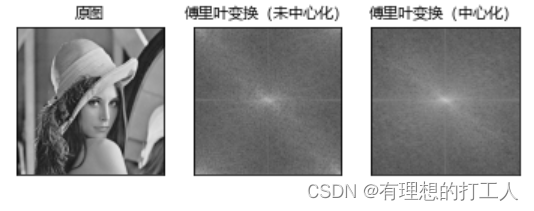
OpenCV给我们提供了可以帮我们对图像矩阵进行傅里叶变换的函数，变换过程如下：

• 使用cv2.dft()或cv2.idft()函数处理图像，需注意输入图像需要先转换成np.float32 格式；
• 处理后得到的矩阵低频分量在各个角落，我们需要把它们拉到图像的中心，这个过程叫做频谱中心化，使用shift变换来实现；
• cv2.dft()返回的结果是双通道的（实部，虚部），通常还需要转换成图像格式才能展示，这一步需要进行20×log_AB运算。

import numpy as np
import cv2
from matplotlib import pyplot as plt
from matplotlib import font_manager
font = font_manager.FontProperties(fname=r"c:\windows\fonts\msyh.ttc", size=10)

img = cv2.imread('lena.jpg',0)

img_float32 = np.float32(img) # 格式转换
# 傅里叶变换
dft = cv2.dft(img_float32, flags = cv2.DFT_COMPLEX_OUTPUT)
# 频谱中心化
dft_shift = np.fft.fftshift(dft)
# 得到灰度图能表示的形式
magnitude_spectrum1 = 20*np.log(cv2.magnitude(dft[:,:,0],dft_shift[:,:,1]))
magnitude_spectrum2 = 20*np.log(cv2.magnitude(dft_shift[:,:,0],dft_shift[:,:,1]))

plt.subplot(131),plt.imshow(img, cmap = 'gray'),plt.title('原图',fontproperties=font)
plt.xticks([]), plt.yticks([])
plt.subplot(132),plt.imshow(magnitude_spectrum1, cmap = 'gray'),plt.title('傅里叶变换（未中心化）',fontproperties=font)
plt.xticks([]), plt.yticks([])
plt.subplot(133),plt.imshow(magnitude_spectrum2, cmap = 'gray'),plt.title('傅里叶变换（中心化）',fontproperties=font)
plt.xticks([]), plt.yticks([])
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

滤波

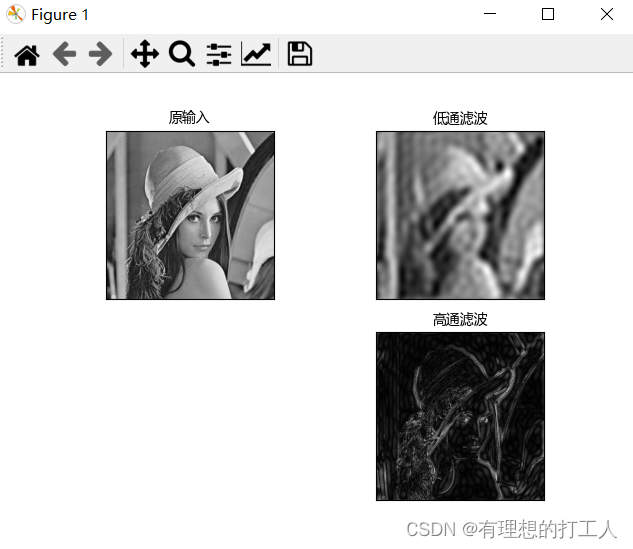
滤波分为高通滤波和低通滤波，高通滤波就是利用掩码把中心化傅里叶变换图像中中心点附近的值遮住，低通滤波刚好相反，把中心点附近的内容保留，其余部分值遮住。滤波工作做完之后，我们还需要进行去中心化（使用ifftshift函数）和逆傅里叶变换（使用idft函数）才能显示图像：

img = cv2.imread('lena.jpg',0)
img_float32 = np.float32(img)
dft = cv2.dft(img_float32, flags = cv2.DFT_COMPLEX_OUTPUT)
dft_shift = np.fft.fftshift(dft)

rows, cols = img.shape
crow, ccol = int(rows/2) , int(cols/2)     # 找到中心位置

# 低通滤波掩膜
mask = np.zeros((rows, cols, 2), np.uint8)
for i in range(rows):
    for j in range(cols):
        if (i-crow)**2+(j-ccol)**2<=15**2:
            mask[i, j] = 1
# 高通滤波掩膜
mask2=np.ones((rows, cols, 2), np.uint8)
for i in range(rows):
    for j in range(cols):
        if (i-crow)**2+(j-ccol)**2<=15**2:
            mask2[i, j] = 0

# 滤波
fshift = dft_shift*mask   # 低通滤波
fshift2 = dft_shift*mask2 # 高通滤波
# 去中心化
f_ishift = np.fft.ifftshift(fshift)
f_ishift2 = np.fft.ifftshift(fshift2)
# 傅里叶逆变换
img_back1 = cv2.idft(f_ishift)
img_back2 = cv2.idft(f_ishift2)
# 转换成可显示的图像矩阵
img_back1 = cv2.magnitude(img_back1[:,:,0],img_back1[:,:,1])
img_back2 = cv2.magnitude(img_back2[:,:,0],img_back2[:,:,1])

plt.subplot(221),plt.imshow(img, cmap = 'gray')
plt.title('原输入',fontproperties=font), plt.xticks([]), plt.yticks([])
plt.subplot(222),plt.imshow(img_back1, cmap = 'gray')
plt.title('低通滤波',fontproperties=font), plt.xticks([]), plt.yticks([])
plt.subplot(224),plt.imshow(img_back2, cmap = 'gray')
plt.title('高通滤波',fontproperties=font), plt.xticks([]), plt.yticks([])

plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

滤波除了可以帮我们把低频信息和高频信息分开，还可以帮我们除掉噪声。现实中的图片很多必须先经过滤噪才可以继续进行其他操作，因此傅里叶变换的地位也就十分重要了。
今天的内容就到这了，小伙伴们下次见咯~