-
机器学习之期末复习
一、模拟退火
模拟退火算法最早的思想由Metropolis等(1953)提出。算法的目的是:(1)解决NP复杂性问题;(2)克服优化过程陷入局部极小;(3)克服初值依赖性。模拟退火算法的提出受到了自然界的启发 —— 物质总是趋于最低的能态,因为最低能态是最稳定的能态。自然界种,只要温度上升得足够高,冷却过程足够慢,则所有粒子最终会处于最低能态(最低的熵值);模拟退火也是这样,只要初温足够高,温度下降足够慢,一定能达到全局最优点。
模拟退火可以看作是爬山法的改进,创新之处是能够以一定概率接受比原来差的状态,使得能够在局部最低点跳出去,有可能向着全局最优点移动。过程如下:给定初温t=t0,随机产生初始状态s=s0,令k=0; Repeat Repeat 产生新状态sj=Generate(s); if min{1,exp[-(C(sj)-C(s))/tk]}>=randrom[0,1] s=sj; Until 抽样稳定准则满足; 退温tk+1=update(tk) 并 令k=k+1; Until 算法终止准则满足; 输出算法搜索结果- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
模拟退火算法的核心是三函数、两准则:(1)状态产生函数;(2)状态接受函数;(3)温度更新函数;(4)抽样稳定准则;(5)算法终止准则
其中算法终止准则包括:(1)零度法;(2)循环总数控制法;(3)基于不改进规则的控制法;(4)接受概率控制法


二、聚类算法
1. K-means聚类
① 从D中随机取k个元素,作为k个簇的各自的中心。 ② 分别计算剩下的元素到k个簇中心的相异度,将这些元素分别划归到相异度最低的簇。 ③ 根据聚类结果,重新计算k个簇各自的中心,计算方法是取簇中所有元素各自维度的算术平均数。 ④ 将D中全部元素按照新的中心重新聚类。 ⑤ 重复第4步,直到聚类结果不再变化。 ⑥ 将结果输出。- 1
- 2
- 3
- 4
- 5
- 6

2. AGNES层次聚类
AGNES(自底向上凝聚算法)计算机编程实现: 输入:包含n个对象的数据库,终止条件簇的数目k。 输出:k个簇,达到终止条件规定簇数目。 将每个对象当成一个初始簇 REPEAT 根据两个簇中最近的数据点找到最近的两个簇; 合并两个簇,生成新的簇的集合; UNTIL 达到定义的簇的数目- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
其中判断两个簇的相似度一共阐述了三种方法:(1)SingleLinkage;(2)CompleteLinkage;(3)Average-Linkage

3. DBSCSAN密度聚类
DBSCAN算法描述 输入:包含n个对象的数据库,半径ε,最少数目MinPts。 输出:所有生成的簇,达到密度要求。 1. REPEAT 2. 从数据库中抽取一个未处理过的点; 3. IF 抽出的点是核心点 THEN 找出所有从该点密度可达的对象,形成一个簇 4. ELSE 抽出的点是边缘点(非核心对象),跳出本次循环,寻找下一点; 5. UNTIL 所有点都被处理;- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8

三、决策树
1. ID3


2. 评价矩阵
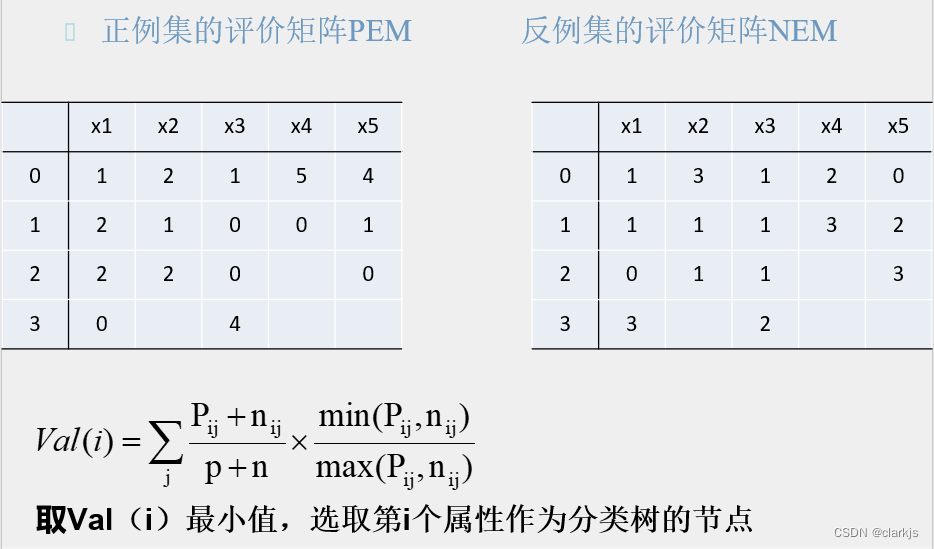
3. 决策树剪枝

参考链接:https://blog.csdn.net/Vicky_xiduoduo/article/details/123497220四、遗传算法
1. 顺序编码的合法性恢复

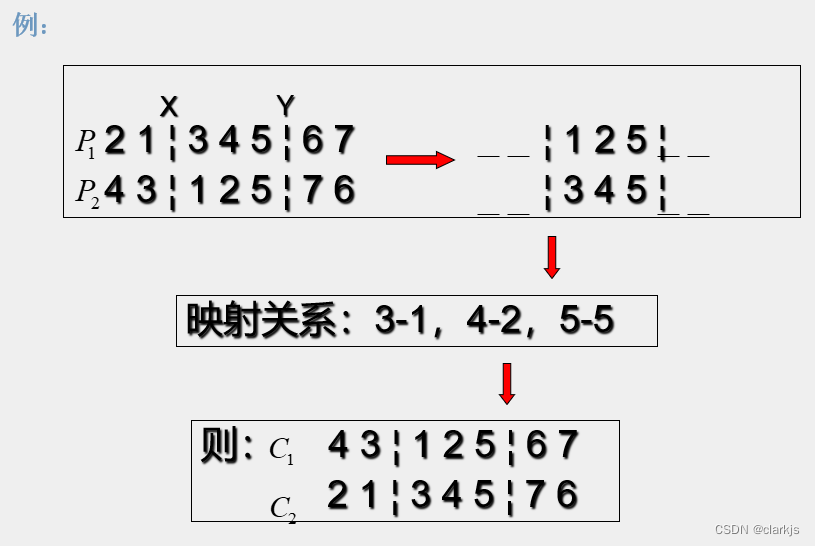

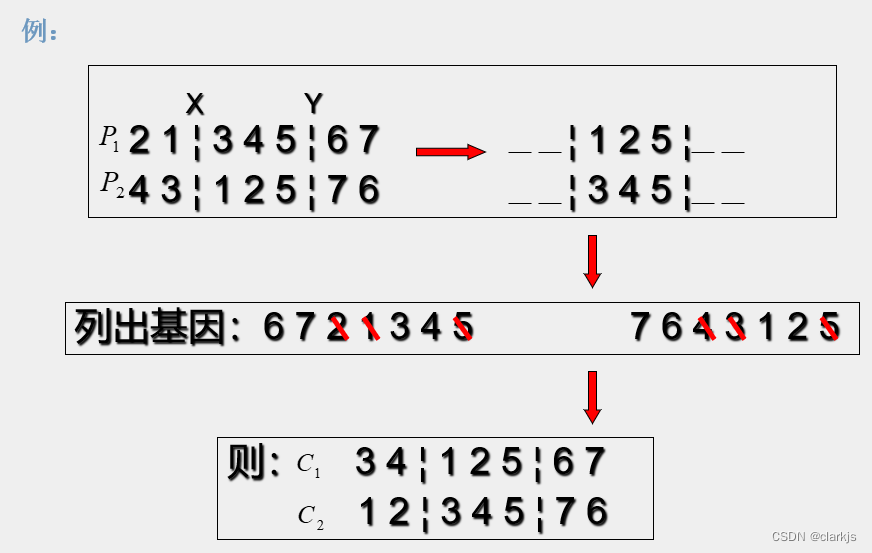



五、线性回归
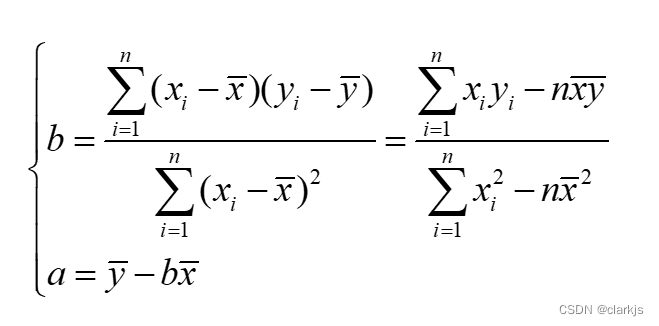
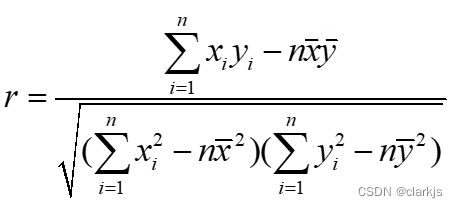
六、覆盖算法
1. AQ15

2. 扩张矩阵算法AE

3. FCV算法
PE‘= PE; NE’= NE step1: 建立PE的评价矩阵PEM和NE的评价矩阵NEM; step2:For( i =0; i< N; i++) For(j=0; j<F; j++) 求PEM[i,j]/NEM[i,j]最小值; Step3:在PE和NE中删除第j个属性的取值为i的例子; Step4:如果NE不空,重复Step1;否则建立PE在NE'的扩张矩阵EM,寻找一个公共路径,即覆盖规则; PE‘=PE’-PE; PE=PE‘; NE=NE’; 重复上面步骤,直到PE’为空,即得到覆盖正例集PE,排斥反例集NE的所有覆盖规则- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
七、数据挖掘
1. APRIORI

直到无法继续产生候选集时,算法停止。
APRIORI算法分为两个阶段:(1)找频繁项集;(2)根据频繁集找关联规则2. 频繁增长模式 (FP树)

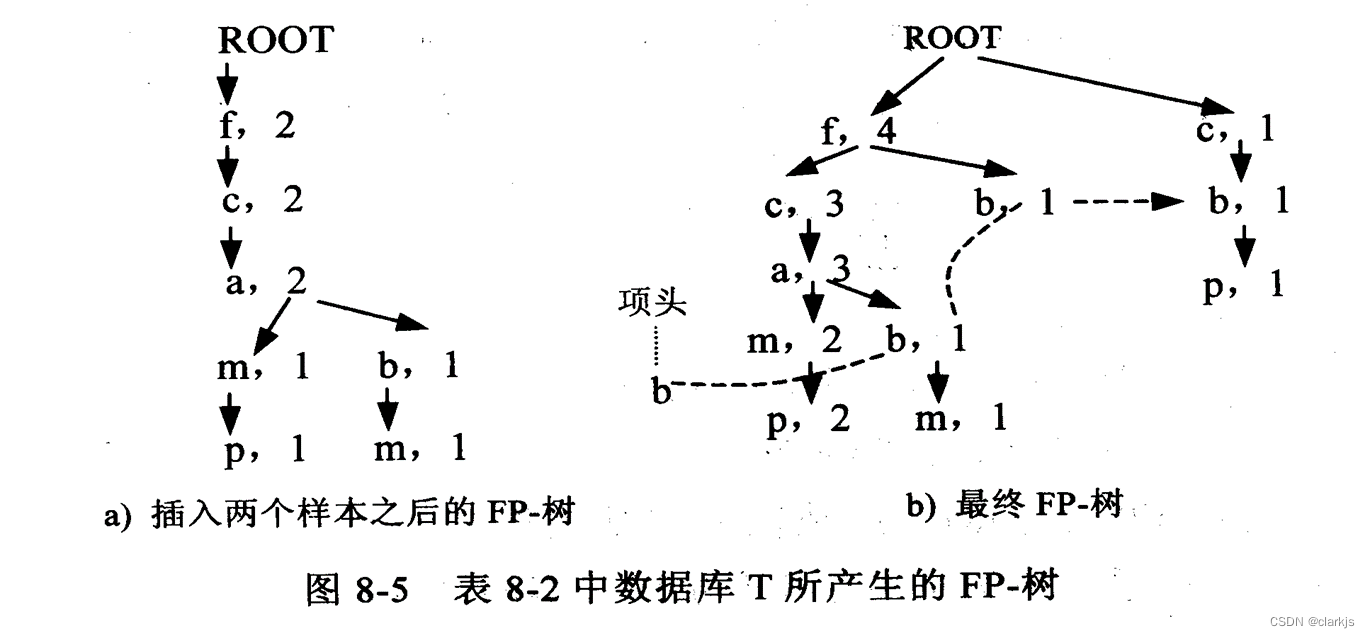
-
相关阅读:
【最全最详细Docker】用docker部署mysql、tomcat、nginx、redis 环境部署
C++类的继承
Appium自动化测试<三>
【英雄哥七月集训】第 04天:贪心
【JavaSE】类和对象——上
O2OA(翱途)开发平台 V8.1正式发布
直销系统开发是找开发公司还是外包团队?
Bcrypt 加密算法
微信小程序入门级
Redis源码篇(6)——主从复制
- 原文地址:https://blog.csdn.net/m0_51339444/article/details/126479829