结合重心反向变异的飞蛾扑火优化算法

摘要：针对经典飞蛾扑火优化算法（MFO）在寻优过程中容易存在早熟及寻优精度低等问题,本文提出一种改进型飞蛾扑火优化算法（IMFO）。首先,使用佳点集初始化种群,使得初始种群分布更具遍历性;其次,引用惯性权重更新飞蛾位置,平衡算法的开发和探索能力;最后,采用重心反向变异策略对位置进行变异,跳出局部最优。

1.飞蛾扑火优化算法

基础飞蛾扑火优化算法的具体原理参考，我的博客：https://blog.csdn.net/u011835903/article/details/107764895

2. 改进飞蛾扑火优化算法

2.1 佳点集初始化种群

有研究发现, 初始化种群的多样性有利于提高 算法寻优性能 $[7-8]$ 。原始 MFO 算法随机生成初始 种群, 种群多样性不够, 会影响算法收玫速度和精 度。本文利用佳点集理论初始化种群,保证初始种 群在解空间分布更加均匀,具体实现方法如下:
在 $\dim$ 维空间取 $n$ 个点的佳点集, 表示为式
(6)
$$P_n(k)=\left\{\left(\left\{r^{1}k\right\},\cdots ,\left\{r^{i}k\right\},\cdots ,\left\{r^{t}k\right\}\right),k=1,2,\cdots ,n\right\}\text{. }\text{\hspace{1em}(6)}$$
其中, r i = { 2 cos ⁡ ( 2 π i / p ) } ; 1 ⩽ i ⩽ t ; P r^{i}=\{2 \cos (2 \pi i / p)\} ; 1 \leqslant i \leqslant t ; P ri={2cos(2πi/p)};1⩽i⩽t;P 是满足 $p⩾2t+3$ 的最小素数。

2.2 引入动态惯性权重

对于群智能优化算法, 能很好的协调算法的全 局搜索和局部搜索能力一直是研究热点。由式 (4) 可知,下一代飞蛾位置围绕火焰进行更新, 同时受当 前飞蛾位置影响, 不能很好的平衡算法的全局搜索 和局部搜索能力, 容易陷入局部最优。因此受 PSO 算法启发, 本文在飞蛾位置更新方式中引入动态变 化的惯性权重 $\mathrm{w}$, 新的位置更新公式为式 (7):
$$M_i=w\cdot D_i\cdot e^{bt}\cdot \cos (2\pi t)+(1-w)\cdot F_j,$$
$$w=2\times \left(1-\sin \left(0.5\times \pi \times \left(t/t_{\max }\right)\right)\right)\times \mathrm{rand}()\text{. }$$
其中, $t$ 为当前迭代次数; $t_{\text{max }}$ 为最大迭代次数; $\mathrm{rand}($ ) 为 $[0,1]$ 间随机数, 使得搜索具有无偏性, 用以提高种群多样性。随着算法迭代,$t/t_{\max }$ 变化近似于0 到1，使得 w 最开始较大，在迭代后期，w 逐渐趋于 0，使算法不易陷入局部最优且收敛加快。

2.3 重心反向变异

为提升种群多样性, 扩大搜索范围, 常用的办法 就是引入变异策略, 产生变异飞蛾, 帮助算法逃离局 部最优。本文引用重心反向学习策略, 在算法迭代 前期, 种群个体差异较大, 变异飞蛾的产生可以探索 更多的区域, 在算法迭代后期, 种群个体数减少, 变 异飞蛾仍然能保留多样性 ${}^{[9]}$ 。重心定义如下:
设 $\left(m_{1j},m_{2j},\cdots ,m_{nj}\right)$ 为 $n$ 个飞蛾在第 $j$ 维的取 值, 种群个体数为 $N$, 则飞蛾种群在第 $j$ 维的重心为 式 (9), 种群重心为 $Z=\left(z_1,z_2,\cdots ,z_j\right)$ 。
$$Z_j=\frac{x_{1j}+x_{2j}+\cdots +x_{nj}}{n}.$$
重心反向变异: 设 $x_i=\left(x_{i1},x_{i2},\cdots ,x_{iD}\right)$ 为飞蛾
$i$, 飞蛾维度是 $D$ 维, 选取的变异维度是第 $j$ 维, 则飞 $x_{o_{-}iD})$, 由式 (10) 确定:
$$x_{op-i}=2\times k\times Z_j-x_i.$$
其中, $k$ 是收缩因子, 取值为 $[0,1]$ 间的随机 数。迭代过程中, 对飞蛾种群的每一只飞蛾选取某 一维度 $j$ 进行变异, 变异结果与上一代位置进行比 较, 保留较优变异。

算法步骤：

Step 1 设定算法参数: 种群规模 $N、$ 维度 dim、 最大迭代次数 $t_{\max }$;

Step 2 参考式 (6) 佳点集理论初始化种群位 置;

Step 3 计算飞蛾和火焰的适应度值, 计算火 焰个数, 合并飞蛾和火焰, 并按适应度值大小进行排 序;
Step 4 利用式 (7) 进行飞蛾位置更新;
Step 5 根据式 (10) 进行重心反向变异, 保存 较优变异;

Step 6 若满足终止条件, 则输出最优个体值 和全局最优解, 算法结束; 否则, 返回 Step 3。

3.实验结果

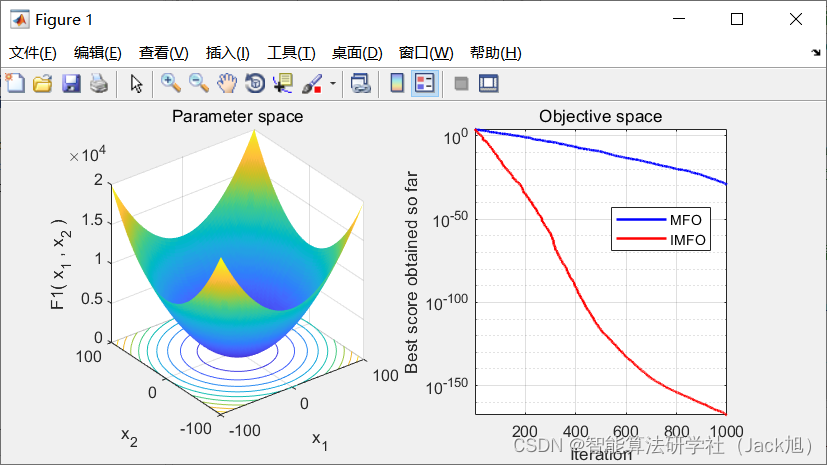
4.参考文献

[1]宋婷婷,张琳娜.结合重心反向变异的飞蛾扑火优化算法[J].智能计算机与应用,2020,10(12):104-107+115.

5.Matlab代码

6.Python代码