深度学习二三事-循环神经网络回顾

前言

         卷积神经网络从2012年开始逐步火热起来。我是在2017年开始接触深度学习技术，完成硕士课题研究，在2019年毕业后以算法工程师职位进入AI创业公司，如今工作3年了。俗话说，温故而知新，结合自己这几年的工作经验，再重新回顾一些那些年是一知半解的，经典的深度学习网络，从大牛的视野看这些网络的设计和迭代。希望对今后工作学习更有帮助。

        互联网的兴起带来的好处之一是，只要你想学习，总有很多免费网络资源。而学术界的研究院，科学家们也在不遗余力的推广深度学习技术，让更多的人了解入门深度学习，做了很多免费的视频课，出了相关的书。本系列博文的内容就是来自于亚马逊资深首席科学家、AI大牛李沐的D2L-ai系列课程。博文内容大多数来自该课程，主要是自己的学习笔记，以及个别思考，重新完善自己的知识体系。

序言 — 动手学深度学习 2.0.0-beta0 documentation

GitHub - d2l-ai/d2l-zh: 《动手学深度学习》：面向中文读者、能运行、可讨论。中英文版被55个国家的300所大学用于教学。
 

序列模型

        电影推荐，股价预测往往与很多因素有关，并且具有时间维度的规律，本质上，音乐、语音、文本和视频都是连续的，如果他们的序列被重排，那么就会失去原有的意义。 这些场景都是序列数据。

        在统计学中，对超出已知观测范围进行预测的情况称为外推法（extrapolation）， 而在现有观测值之间进行估计的情况称为内插法（interpolation）。外推法比内插法更困难，毕竟先见之明比事后诸葛亮难得多。

        自回归模型和马尔可夫模型，基于序列模型前后时间的因果概率关系，来预测未来的股价变动，在许多情况下，数据存在一个自然的方向，即在时间上是前进的。 很明显，未来的事件不能影响过去。

小结

• 内插法（在现有观测值之间进行估计）和外推法（对超出已知观测范围进行预测）在实践的难度上差别很大。因此，对于你所拥有的序列数据，在训练时始终要尊重其时间顺序，即最好不要基于未来的数据进行训练。
• 序列模型的估计需要专门的统计工具，两种较流行的选择是自回归模型和隐变量自回归模型。
• 对于时间是向前推进的因果模型，正向估计通常比反向估计更容易。
• 对于直到时间步𝑡t的观测序列，其在时间步𝑡+𝑘t+k的预测输出是“𝑘k步预测”。随着我们对预测时间𝑘k值的增加，会造成误差的快速累积和预测质量的极速下降。

文本预处理

        序列数据存在很多格式，文本是常见的例子之一，例如，一篇文章可以被简单的看作是一串单词序列，或者字符串序列，文本的常见预处理步骤包括：

1. 将文本作为字符串加载到内存中。
2. 将字符串拆分为词元（如单词和字符）。
3. 建立一个词表，将拆分的词元映射到数字索引。
4. 将文本转换为数字索引序列，方便模型操作。

词元化

将文本行列表分割为一个个的单词列表，即词元列表。如

行列表：‘the time machine by h g wells’

词元列表：['the', 'time', 'machine', 'by', 'h', 'g', 'wells']

词表

        词元的类型是字符串，而模型需要的输入是数字，因此这种类型不方便模型使用。 现在，让我们[构建一个字典，通常也叫做词表（vocabulary）， 用来将字符串类型的词元映射到从00开始的数字索引中]。 我们先将训练集中的所有文档合并在一起，对它们的唯一词元进行统计， 得到的统计结果称之为语料（corpus）。 然后根据每个唯一词元的出现频率，为其分配一个数字索引。 很少出现的词元通常被移除，这可以降低复杂性。 另外，语料库中不存在或已删除的任何词元都将映射到一个特定的未知词元“”。 我们可以选择增加一个列表，用于保存那些被保留的词元， 例如：填充词元（“”）； 序列开始词元（“”）； 序列结束词元（“”）。

词表：

[('', 0), ('the', 1), ('i', 2), ('and', 3), ('of', 4), ('a', 5), ('to', 6), ('was', 7), ('in', 8), ('that', 9)]

将一行文本转为数字索引列表：

文本: ['the', 'time', 'machine', 'by', 'h', 'g', 'wells']
索引: [1, 19, 50, 40, 2183, 2184, 400]

小结

• 文本是序列数据的一种最常见的形式之一。
• 为了对文本进行预处理，我们通常将文本拆分为词元，构建词表将词元字符串映射为数字索引，并将文本数据转换为词元索引以供模型操作。

循环神经网络

        无隐状态的神经网络类似只有单隐藏层的错层感知机，隐藏变量H直接作为输出层的输入求出，通过自动微分和随机梯度下降能够学习网络参数就可以了。

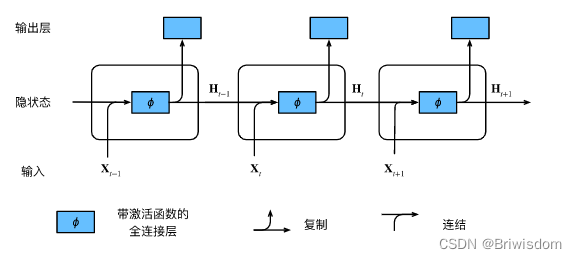
有隐状态的循环神经网络

        假设我们在时间步𝑡有小批量输入𝐗𝑡∈ℝ𝑛×𝑑。 换言之，对于𝑛个序列样本的小批量， 𝐗𝑡的每一行对应于来自该序列的时间步𝑡处的一个样本。 接下来，用𝐇𝑡∈ℝ𝑛×ℎ表示时间步𝑡t的隐藏变量。 与多层感知机不同的是， 我们在这里保存了前一个时间步的隐藏变量𝐇𝑡−1， 并引入了一个新的权重参数𝐖ℎℎ∈ℝℎ×ℎ， 来描述如何在当前时间步中使用前一个时间步的隐藏变量。 具体地说，当前时间步隐藏变量由当前时间步的输入 与前一个时间步的隐藏变量一起计算得出：

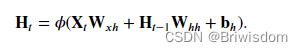
 在任意时间步𝑡，隐状态的计算可以被视为：

1. 拼接当前时间步𝑡的输入𝐗𝑡和前一时间步𝑡−1的隐状态𝐇𝑡−1；
2. 将拼接的结果送入带有激活函数𝜙的全连接层。 全连接层的输出是当前时间步𝑡的隐状态𝐇𝑡。

困惑度

         接下来我们将一起讨论如何度量语言模型的质量。

        我们可以通过计算序列的似然概率来度量模型的质量。 然而这是一个难以理解、难以比较的数字。 毕竟，较短的序列比较长的序列更有可能出现， 因此评估模型产生托尔斯泰的巨著《战争与和平》的可能性 不可避免地会比产生圣埃克苏佩里的中篇小说《小王子》可能性要小得多。 而缺少的可能性值相当于平均数。

        在这里，信息论可以派上用场了。 我们在引入softmax回归时定义了熵、惊异和交叉熵， 并在信息论的在线附录 中讨论了更多的信息论知识。 如果想要压缩文本，我们可以根据当前词元集预测的下一个词元。 一个更好的语言模型应该能让我们更准确地预测下一个词元。 因此，它应该允许我们在压缩序列时花费更少的比特。 所以我们可以通过一个序列中所有的𝑛个词元的交叉熵损失的平均值来衡量：

        其中𝑃由语言模型给出， 𝑥𝑡是在时间步𝑡t从该序列中观察到的实际词元。 这使得不同长度的文档的性能具有了可比性。 由于历史原因，自然语言处理的科学家更喜欢使用一个叫做困惑度（perplexity）的量。 简而言之，它是交叉熵损失平均值的指数：

        困惑度的最好的理解是“下一个词元的实际选择数的调和平均数”。 我们看看一些案例：

• 在最好的情况下，模型总是完美地估计标签词元的概率为1。 在这种情况下，模型的困惑度为1。
• 在最坏的情况下，模型总是预测标签词元的概率为0。 在这种情况下，困惑度是正无穷大。
• 在基线上，该模型的预测是词表的所有可用词元上的均匀分布。 在这种情况下，困惑度等于词表中唯一词元的数量。 事实上，如果我们在没有任何压缩的情况下存储序列， 这将是我们能做的最好的编码方式。 因此，这种方式提供了一个重要的上限， 而任何实际模型都必须超越这个上限。

小结

• 对隐状态使用循环计算的神经网络称为循环神经网络（RNN）。
• 循环神经网络的隐状态可以捕获直到当前时间步序列的历史信息。
• 循环神经网络模型的参数数量不会随着时间步的增加而增加。
• 我们可以使用循环神经网络创建字符级语言模型。
• 我们可以使用困惑度来评价语言模型的质量。

循环神经网络的实现代码：8.5. 循环神经网络的从零开始实现 — 动手学深度学习 2.0.0-beta1 documentation

总结

• 循环神经网络的输出取决于当下输入和前一时间的隐变量
• 应用到语言模型中，循环神经网络根据当前词预测下一次时刻词
• 通常使用困惑度来衡量语言模型的好坏

LSTM模型

        长期以来，隐变量模型存在着长期信息保存和短期输入缺失的问题。 解决这一问题的最早方法之一是长短期存储器（long short-term memory，LSTM） [Hochreiter & Schmidhuber, 1997]。 它有许多与门控循环单元（ 9.1节）一样的属性。 有趣的是，长短期记忆网络的设计比门控循环单元稍微复杂一些， 却比门控循环单元早诞生了近20年。

        长短期记忆网络的设计灵感来自于计算机的逻辑门。 长短期记忆网络引入了记忆元（memory cell），或简称为单元（cell）。 有些文献认为记忆元是隐状态的一种特殊类型， 它们与隐状态具有相同的形状，其设计目的是用于记录附加的信息。 为了控制记忆元，我们需要许多门。 其中一个门用来从单元中输出条目，我们将其称为输出门（output gate）。 另外一个门用来决定何时将数据读入单元，我们将其称为输入门（input gate）。 我们还需要一种机制来重置单元的内容，由遗忘门（forget gate）来管理， 这种设计的动机与门控循环单元相同， 能够通过专用机制决定什么时候记忆或忽略隐状态中的输入。

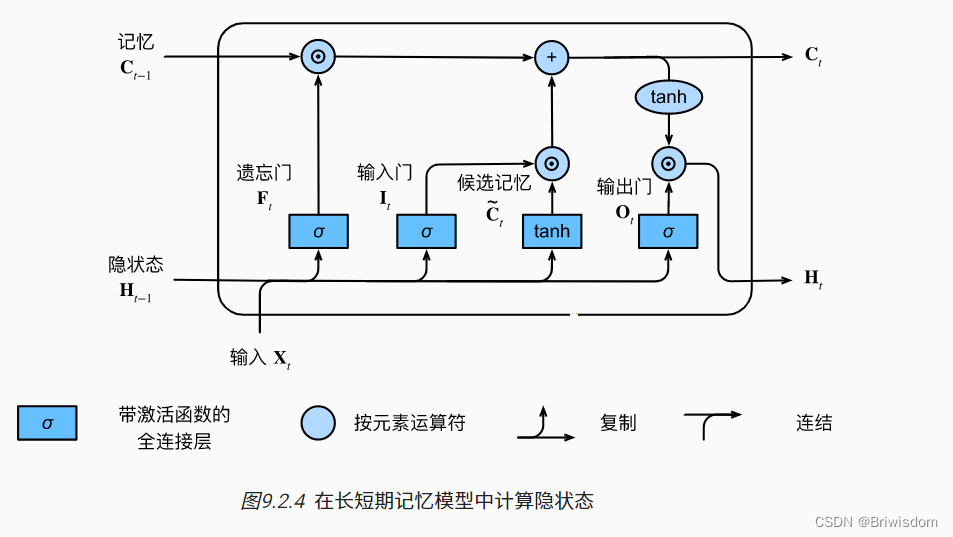
 如下是lstm几个门的具体计算过程。

def lstm(inputs, state, params):
    [W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc, b_c,
     W_hq, b_q] = params
    (H, C) = state
    outputs = []
    for X in inputs:
        I = torch.sigmoid((X @ W_xi) + (H @ W_hi) + b_i)
        F = torch.sigmoid((X @ W_xf) + (H @ W_hf) + b_f)
        O = torch.sigmoid((X @ W_xo) + (H @ W_ho) + b_o)
        C_tilda = torch.tanh((X @ W_xc) + (H @ W_hc) + b_c)
        C = F * C + I * C_tilda
        H = O * torch.tanh(C)
        Y = (H @ W_hq) + b_q
        outputs.append(Y)
    return torch.cat(outputs, dim=0), (H, C)

 小结

• 长短期记忆网络有三种类型的门：输入门、遗忘门和输出门。

• 长短期记忆网络的隐藏层输出包括“隐状态”和“记忆元”。只有隐状态会传递到输出层，而记忆元完全属于内部信息。

• 长短期记忆网络可以缓解梯度消失和梯度爆炸。

深度循环神经网络

        到目前为止，我们只讨论了具有一个单向隐藏层的循环神经网络。 其中，隐变量和观测值与具体的函数形式的交互方式是相当随意的。

         只要交互类型建模具有足够的灵活性，这就不是一个大问题。 然而，对于一个单层来说，这可能具有相当的挑战性。 之前在线性模型中，我们通过添加更多的层来解决这个问题。 而在循环神经网络中，我们首先需要确定如何添加更多的层， 以及在哪里添加额外的非线性，因此这个问题有点棘手。

        事实上，我们可以将多层循环神经网络堆叠在一起， 通过对几个简单层的组合，产生了一个灵活的机制。 特别是，数据可能与不同层的堆叠有关。 例如，我们可能希望保持有关金融市场状况 （熊市或牛市）的宏观数据可用， 而微观数据只记录较短期的时间动态。

图9.3.1描述了一个具有L个隐藏层的深度循环神经网络， 每个隐状态都连续地传递到当前层的下一个时间步和下一层的当前时间步。

 小结

• 在深度循环神经网络中，隐状态的信息被传递到当前层的下一时间步和下一层的当前时间步。

• 有许多不同风格的深度循环神经网络， 如长短期记忆网络、门控循环单元、或经典循环神经网络。 这些模型在深度学习框架的高级API中都有涵盖。

• 总体而言，深度循环神经网络需要大量的调参（如学习率和修剪） 来确保合适的收敛，模型的初始化也需要谨慎。

双向循环神经网络

        如果我们希望在循环神经网络中拥有一种机制， 使之能够提供与隐马尔可夫模型类似的前瞻能力， 我们就需要修改循环神经网络的设计。 幸运的是，这在概念上很容易， 只需要增加一个“从最后一个词元开始从后向前运行”的循环神经网络， 而不是只有一个在前向模式下“从第一个词元开始运行”的循环神经网络。 双向循环神经网络（bidirectional RNNs） 添加了反向传递信息的隐藏层，以便更灵活地处理此类信息。 图9.4.2描述了具有单个隐藏层的双向循环神经网络的架构。

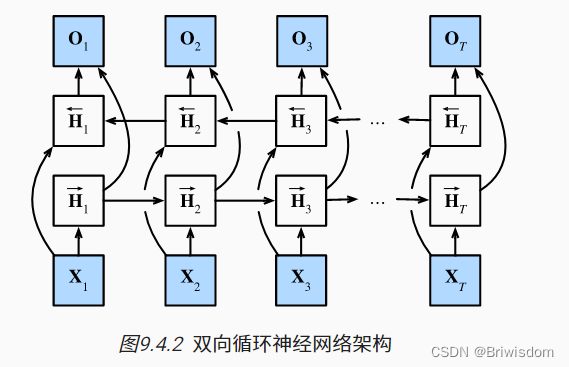
 模型的计算代价及其应用

        双向循环神经网络的一个关键特性是：使用来自序列两端的信息来估计输出。 也就是说，我们使用来自过去和未来的观测信息来预测当前的观测。 但是在对下一个词元进行预测的情况中，这样的模型并不是我们所需的。 因为在预测下一个词元时，我们终究无法知道下一个词元的下文是什么， 所以将不会得到很好的精度。 具体地说，在训练期间，我们能够利用过去和未来的数据来估计现在空缺的词； 而在测试期间，我们只有过去的数据，因此精度将会很差。 下面的实验将说明这一点。

        另一个严重问题是，双向循环神经网络的计算速度非常慢。 其主要原因是网络的前向传播需要在双向层中进行前向和后向递归， 并且网络的反向传播还依赖于前向传播的结果。 因此，梯度求解将有一个非常长的链。

        双向层的使用在实践中非常少，并且仅仅应用于部分场合。 例如，填充缺失的单词、词元注释（例如，用于命名实体识别） 以及作为序列处理流水线中的一个步骤对序列进行编码（例如，用于机器翻译）

小结

• 在双向循环神经网络中，每个时间步的隐状态由当前时间步的前后数据同时决定。

• 双向循环神经网络与概率图模型中的“前向-后向”算法具有相似性。

• 双向循环神经网络主要用于序列编码和给定双向上下文的观测估计。

• 由于梯度链更长，因此双向循环神经网络的训练代价非常高。

编码器-解码器架构

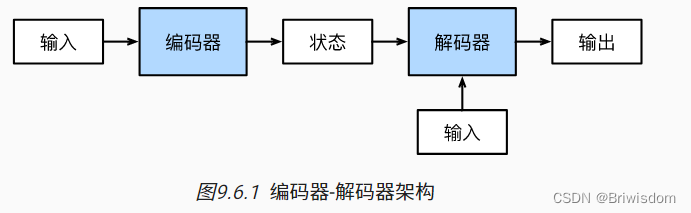
机器翻译是序列转换模型的一个核心问题， 其输入和输出都是长度可变的序列。 为了处理这种类型的输入和输出， 我们可以设计一个包含两个主要组件的架构： 第一个组件是一个编码器（encoder）： 它接受一个长度可变的序列作为输入， 并将其转换为具有固定形状的编码状态。 第二个组件是解码器（decoder）： 它将固定形状的编码状态映射到长度可变的序列。 这被称为编码器-解码器（encoder-decoder）架构， 如 图9.6.1 所示。

小结

• “编码器－解码器”架构可以将长度可变的序列作为输入和输出，因此适用于机器翻译等序列转换问题。

• 编码器将长度可变的序列作为输入，并将其转换为具有固定形状的编码状态。

• 解码器将具有固定形状的编码状态映射为长度可变的序列。