-
【工程光学】理想光学系统
ref 《工程光学》第4版 郁道银
1.共轴理想光学系统成像性质
- 焦点: 光轴上无限远点的共轭点
- 物方焦点: 无限远轴上像点的共轭点
- 物方焦距
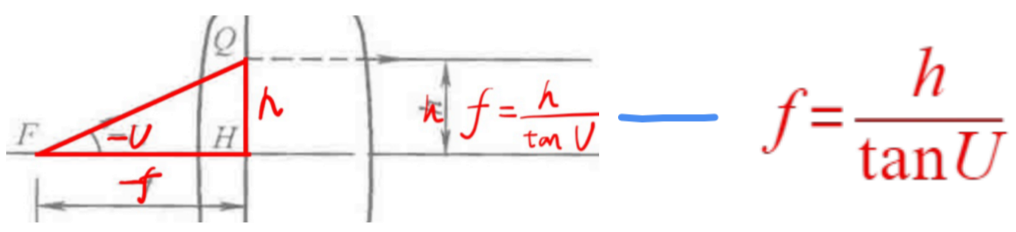
- 像方焦点: 无限远轴上物点的共轭点
- 像方焦距
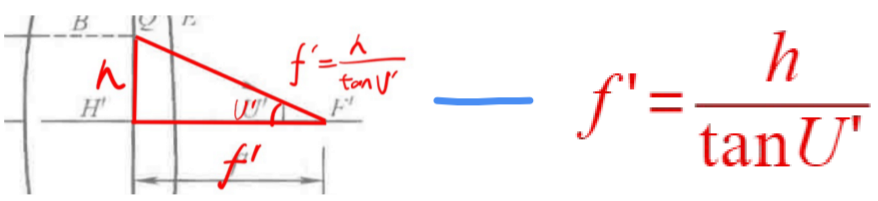
- 焦平面: 过焦点⊥光轴的面
- 主平面:
β
=
±
1
\beta=\pm 1
β=±1的一对共轭平面
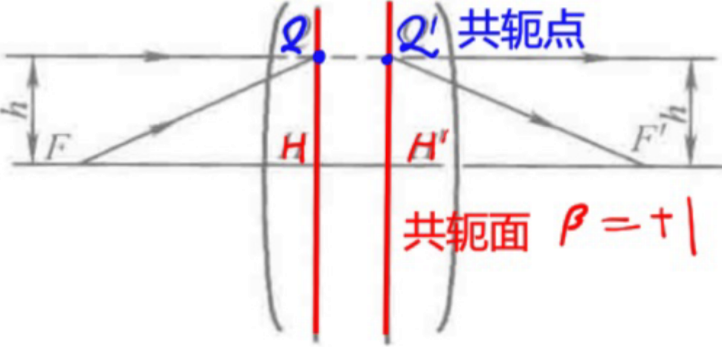
- 主点: 主平面与光轴焦点
- 焦距: 主点到焦点距离
- f ′ f = − n ′ n \frac{f'}{f}=-\frac{n'}{n} ff′=−nn′
- 同一介质中 f ′ = − f f'=-f f′=−f
- 节平面: γ = ± 1 \gamma=\pm 1 γ=±1的一对共轭平面
- 节点: 节平面∩光轴
- x J = f ′ x J ′ = f x_J=f' ~~ x_J'=f xJ=f′ xJ′=f
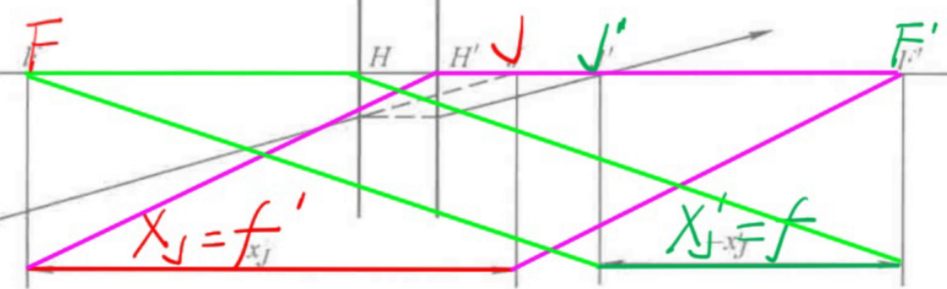
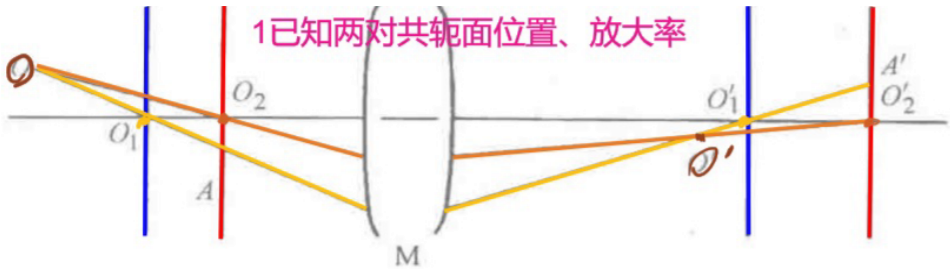
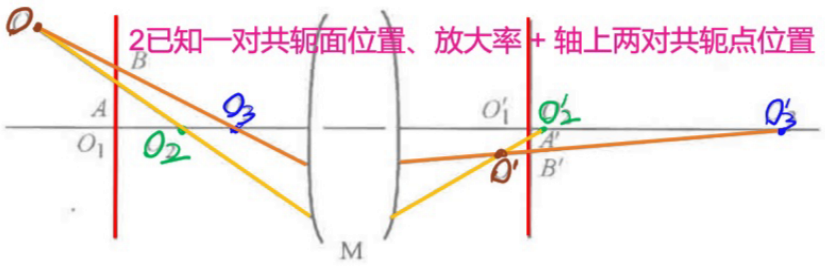
2.成像性质
3.图解法
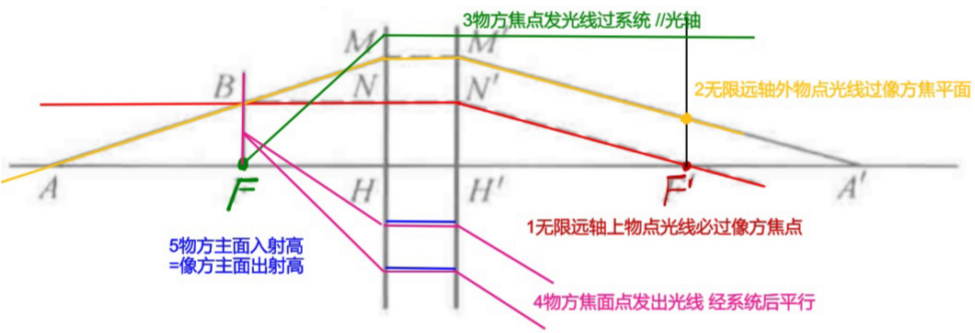
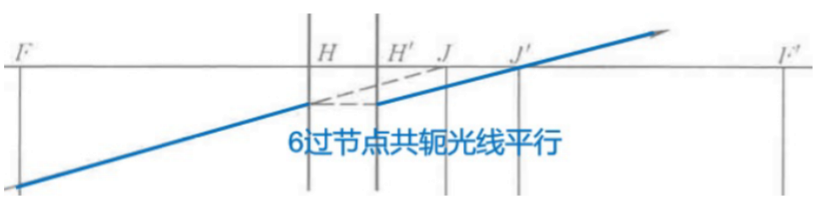
4.解析法
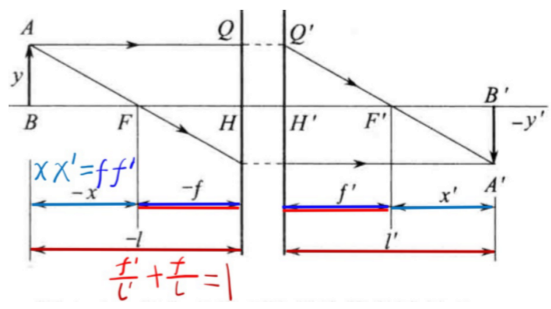
- 牛顿公式
- x x ′ = f f ′ xx'=ff' xx′=ff′
- 高斯公式
- f ′ l ′ + f l = 1 \frac{f'}{l'}+\frac{f}{l}=1 l′f′+lf=1
- 同一介质
- 1 l ′ − 1 l = 1 f ′ \frac{1}{l'}-\frac{1}{l}=\frac{1}{f'} l′1−l1=f′1
- 焦距关系
- f ′ f = − n ′ n \frac{f'}{f}=-\frac{n'}{n} ff′=−nn′
5.理想光学系统放大率
- 垂轴放大率
- β = y ′ y \beta=\frac{y'}{y} β=yy′
- β = − f f ′ l ′ l = n n ′ l ′ l β = − f x = − x ′ f ′ \beta=-\frac{f}{f'}\frac{l'}{l}=\frac{n}{n'}\frac{l'}{l} ~~~~ \beta=-\frac{f}{x}=-\frac{x'}{f'} β=−f′fll′=n′nll′ β=−xf=−f′x′
- 轴向放大率
- α = d x ′ d x = d l ′ d l \alpha=\frac{dx'}{dx}=\frac{dl'}{dl} α=dxdx′=dldl′
- α = − f ′ f β 2 = n ′ n β 2 α = − x ′ x \alpha=-\frac{f'}{f}\beta^2=\frac{n'}{n}\beta^2 ~~~~ \alpha=-\frac{x'}{x} α=−ff′β2=nn′β2 α=−xx′
- 角放大率
- γ = tan U ′ tan U \gamma=\frac{\tan U'}{\tan U} γ=tanUtanU′
- γ = n n ′ 1 β \gamma=\frac{n}{n'}\frac{1}{\beta} γ=n′nβ1
- α γ = β \alpha\gamma=\beta αγ=β
6.光学系统组合公式
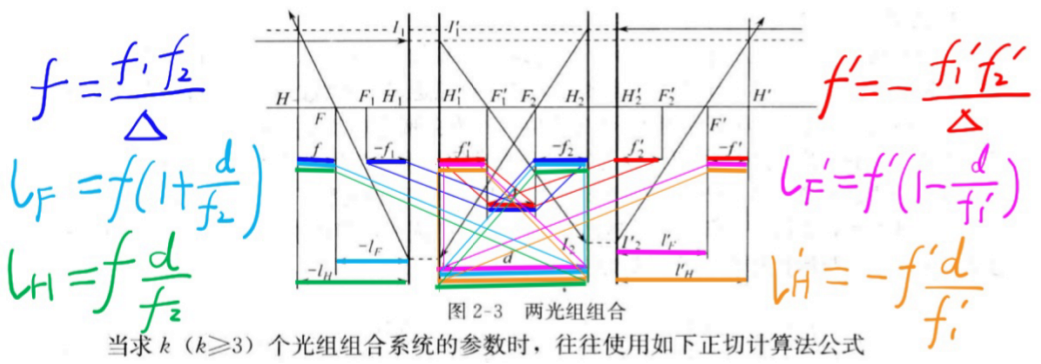
- 光焦度:
- φ 1 = 1 f 1 ′ , φ 2 = 1 f 2 ′ \varphi_1=\frac{1}{f_1'}, \varphi_2=\frac{1}{f_2'} φ1=f1′1,φ2=f2′1
- φ = φ 1 + φ 2 − d φ 1 φ 2 \varphi=\varphi_1+\varphi_2-d\varphi_1\varphi_2 φ=φ1+φ2−dφ1φ2
远摄型光组
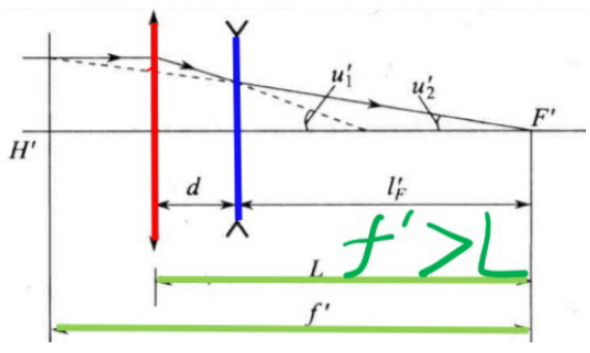
- 正透镜在前, 负透镜在后
- 组合焦距>机械筒长
- 在长焦距镜头中缩小机械尺寸
反远距型光组
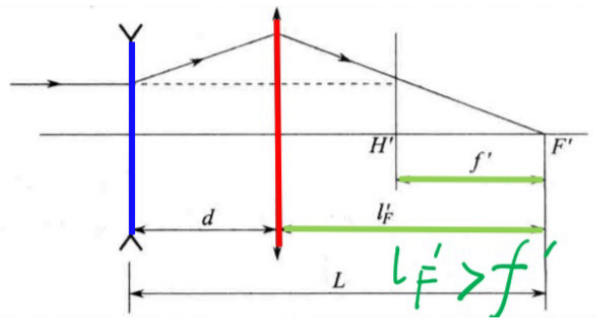
- 负透镜在前, 正透镜在后
- 工作距>焦距
- 短焦距,大工作距镜头(显微镜)
- 焦点: 光轴上无限远点的共轭点
-
相关阅读:
八、QOS队列调度与报文丢弃
【Maven】jar包冲突原因与最优解决方案
知乎好物推荐怎么做赚钱？该如何做？
【Leetcode】最长递增子序列问题及应用
IdeaVim插件使用记录
AIGC 微调的方法
Python递归次数统计写法及邮件发送失败后的重新发送
贪心算法-以学籍管理系统为例
Web安全：Vulfocus 靶场搭建.（漏洞集成平台）
macOS Monterey安装Jekyll
- 原文地址：https://blog.csdn.net/weixin_46143152/article/details/126438045
