【论文精读】Fast R-CNN

《Fast R-CNN》是同一个作者基于自己之前的R-CNN工作的改进。
Fast R-CNN也是基于深度卷积神经网络用于计算机视觉任务（主要用于目标检测）的算法。
他在R-CNN的基础上进行了大幅创新，比如将目标的分类和定位的步骤进行了统一，实现了端到端的训练、预测流程。
Fast R-CNN在使用VGG-16的主干网络时，训练速度比R-CNN快9倍，测试速度快了213倍，并提升了检测精度。
训练速度比SPPnet快了3倍，测试速度快了10倍，并提升了精度。

本文是对论文的精读总结，我会把每一个点都研究讲透，不仅让大家了解Fast R-CNN，还会总结自己在读论文各个部分时自己的心得总结。
Fast R-CNN的前作R-CNN论文精读可参考我的这篇文章。

背景

为什么提出了Fast R-CNN？
作者指出之前的目标检测算法 R-CNN 和 SPPnet 都存在各种缺点。

R-CNN的缺点

R-CNN的缺点：

1. 训练是是多阶段的。首先需要训练一个CNN网络用于图像特征的提取。
   接着需要训练一个线性SVM分类器，对提取出来的特征进行图片分类。
   最后还需要训练一个回归模型，用于调整目标检测候选框的定位。
2. 训练非常贵。因为是多阶段的目标检测，先需要保存每一张图片上的每一个候选框抽取的特征，然后再进行训练。
   因此，需要将这些特征存到磁盘上。
   不仅提取特征耗时，并且储存特征还耗费空间。
3. 测试时，目标检测速度很慢。一个使用VGG-16主干模型的R-CNN，预测一张图片需要耗费47秒的时间（在GPU）上。

作者指出R-CNN慢的根源在于每一个候选框都使用同个CNN网络前向计算，它们之间存在大量重复运算，没有共享计算资源。
为了解决这个问题，后面有大佬（何凯明等）提出了SPPnet。

SPPnet解决的问题和缺点

SPPnet概要：
SPPnet将整张图片经过一次CNN网络前向计算，在最后进入全连接层之前使用了一个SPP层（空间金字塔池化层），而非普通的最大池化层。如下图。

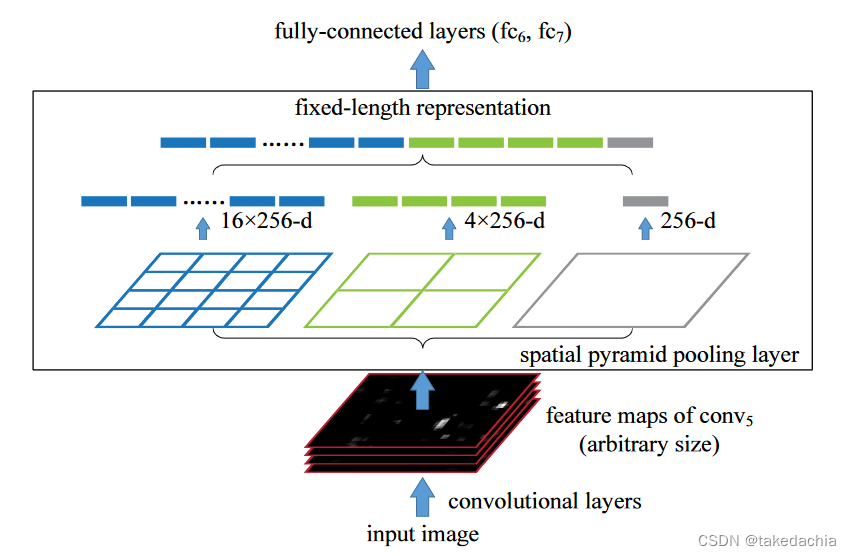
SPP层中，会将卷积层输出的convolutional feature map（图中的feature maps of conv5，它可以任意尺寸）进行一种固定输出的池化，如上图。不管如输入的image的尺寸如何变化，在最后SPP层都会固定输出 1个4×4的特征图、1个2×2的特征图、1个1×1的特征图（具体使用到了动态池化核和步长的算法），类似金字塔堆叠的感觉，最后将这些固定的特征图展品成21×256固定长度的向量传入全连接层。
这样做的好处：
①这里先解决了输入图片固定的问题，让图片无需固定尺寸输入CNN。
②其次每一张图片对应的2000个候选框都可以在最后SPP层前的convolutional feature map中找到对应位置的小区域，将图片中候选框的区域映射到convolutional feature map的对应区域。用抠出来的这块小特征图（下图中的window）进行SPP池化，输出固定特征。（如下图）

这样我们仅需一次前向CNN网络的传播计算，就可以将所有候选框的特征提取出来（不用跑2000次了）。
这就解决了上面R-CNN中共享计算的问题，这会加快检测的速度。
但是SPPnet算法将空间金字塔池化层最后提取到的向量依然使用一个线性SVM分类器和一个回归器进行分类和定位，和R-CNN一样依然是多阶段的。这样依然不能解决R-CNN中多阶段训练慢、耗费资源多的问题（前面的第1、2点）。
并且同时，作者提出了在SPPnet中，使用fine tuning对CNN网络微调训练时，SPP层前的网络参数难以被更新，这会影响目标检测的精度（这个会在后面详述）。

Fast R-CNN的优点

作者提出的Fast R-CNN解决了以上R-CNN和SPPnet的缺点，同时提升了训练和测试速度，并提升精度。
Fast R-CNN的特点：

• 比R-CNN和SPPnet更高的检测精度。
• 使用了一个多任务的损失函数，是一个单阶段的训练过程
• 训练时可更新所有网络层的参数
• 不再需要将提取的候选框特征缓存到磁盘上

Fast R-CNN模型结构

我们来看Fast R-CNN的模型结构（如下图）：
网络的输入为 一张图像+一组目标候选框（也是通过selective search生成）信息。

①图像经过CNN网络后，在最后一个卷积层输出一组Conv feature map。
目标候选框信息，则通过RoI projection，即目标位置的投影，投影定位到Conv feature map对应位置，抠出这块小feature map。

②我们将抠出的这块小feature map传入 RoI pooling layer。
经过这个RoI pooling layer，我们可提取出一个固定长度的特征向量。

③将这个特征向量同时传入两个模块。
传入全连接层+softmax分类，用于预测$K+1$个类别的概率。
传入 bounding-box 回归器，用于预测每一个类别的定位。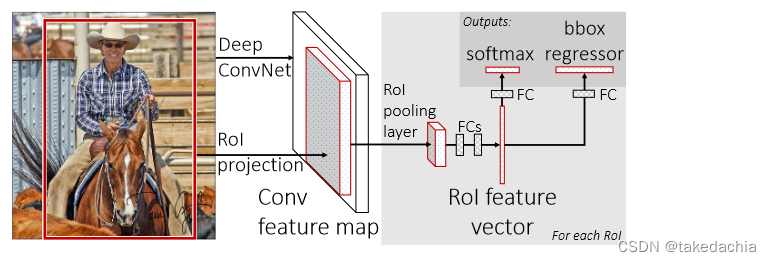

---

可以看到相比R-CNN（下图）而言，该模型有三个不同的地方：

• 传入的不再是目标候选框，而是一整张图片+候选框的定位信息，输出整张图片的feature map。再利用候选框的定位信息进行位置投影，找到候选框在feature map上的对应位置，抠出来传入下一层。这样解决了CNN网络重复计算的问题，不用再对一张图片2000个候选框进行2000次前向计算了，只需1次计算就可以。
• 模型没有对输入的图片进行大小限制，因此输出的 (conv) feature map有大有小，抠出来的小feature map也有大有小。论文使用了 RoI pooling layer，将不同尺寸的小feature map统一池化下采样成固定大小的特征向量（取代了普通CNN网络的最后一个Max Pooling层）。（RoI pooling layer的原理下面细讲）
• 对特征向量进行分类预测时，不再使用线性SVM分类器，而是直接使用softmax输出各个类别的概率。这样就不用再特地对每个类别训练线性SVM分类器了。这个设计也是和单阶段训练的设计相统一，后面会详细讲到。

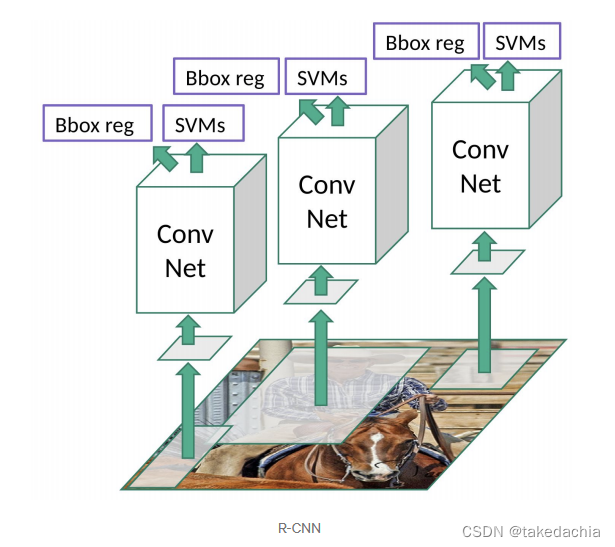
(上图摘自towardsdatascience)

RoI pooling layer

RoI pooling层是一类特殊的自适应Max Pooling层，是一种根据当前feature map尺寸动态指定池化核和步长的Max Pooling，它其实是沿袭了SPPnet中SPP层（空间金字塔池化层）的设计。

我举个两个例子详细地说明RoI pooling layer做了一件什么事：

①假设我们在一个conv feature map中，根据映射关系取到其中一个C×13×13的小feature map进入RoI pooling层，我们想指定输出C×4×4大小的特征向量。
对于我们的Max Pooling：
池化核的size是feature map的size除以输出的size后向上取整，即size=ceil(13/4)=4
步长stride则是feature map的size除以输出的size后向下取整，即size=floor(13/4)=3
这样得到的池化结果正好是一个4×4的输出。
详见下图。最后我们将输出展平，得到C×16的一个特征向量。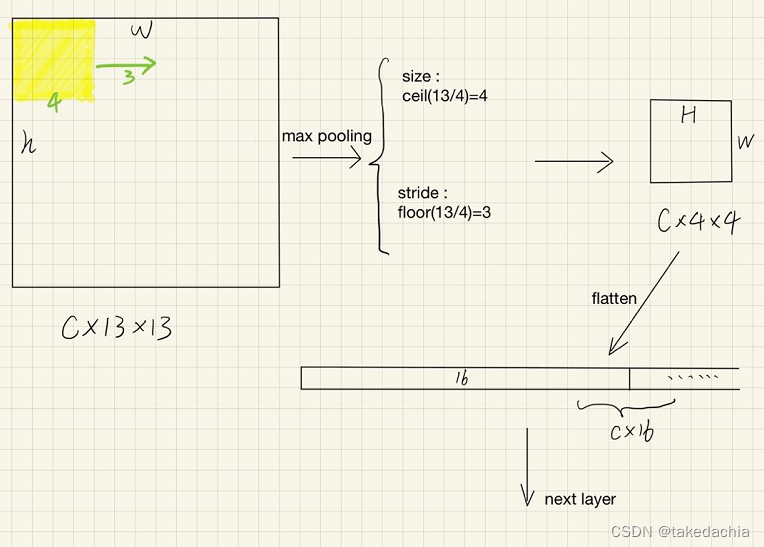

②本例是一个feature map非正方形的例子（图摘自benrishi.ai）
假设我们对图中这个6×4的feature map进行RoI pooling，设定输出2×2大小的特征图。
那么Max pooling的池化核和步长在水平和垂直方向应当各有自己的size和stride。
文中作者并没有详细说明非正方形的情况下如何进行pooling，根据我对作者论文RoI pooling这段描述的理解，矩形feature map的池化参数应为：

kernel_size=( ceil(6/2), ceil(4/2) )=(3,2)
stride=( floor(6/2), floor(4/2) )=(3,2)

即池化核大小为(3,2)，步长在垂直方向为3，水平方向为2。
（PS：也符合Pytorch中nn.MaxPool2d层中的参数规范）
这样池化得到的特征图也是2×2。我们还可以取下图中5×8这张小feature map自行验证一下。

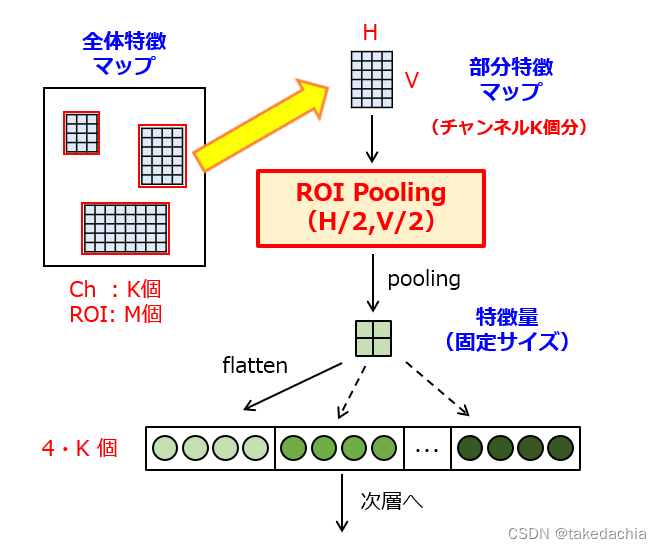
以上就是RoI pooling layer的详解，通过一种的自适应Max Pooling层，固定输出的size。作者自己也说了RoI pooling是借鉴自SPPnet的SPP层，是SPP层的一种特殊情况。

模型的训练细节

总体上模型使用Fine-tuning的方法，对预训练好的图像分类模型修改后进行微调训练。
同时，微调训练是单阶段的流程，即用一个损失函数同时优化softmax和bbox回归器，训练一步到位。（不像R-CNN和SPPnet需要训练3个模块）

构建模型（基于预训练CNN网络进行修改）

作者使用了在ImgeNet图像分类数据集上预训练好的CNN模型（如AlexNet、VGG-16等），对其进行如下修改。

• 将网络最后一个Max Pooling改成RoI Pooling层。
• 将网络最后的全连接+softmax层改成了两个并行的层，即前面所述的：
  ①全连接层+softmax，用于预测$K+1$个类别的概率。
  ② bounding-box 回归器，用于预测每一个类别的定位。
• 将网络的输入改成 图片+图片中目标候选框定位信息。

为什么SPPnet训练时难以更新卷积网络的权重？（关于训练时的采样方法）

作者在文中提到了Fast R-CNN可通过反向传播训练整个网络的权重参数。
论文这里对上面提出的SPPne使用fine tuning对CNN网络微调训练时，网络的参数难以被更新进行了详细解释。
作者在文中使用了"SPPnet is unable to update weights"的说法，我觉得更合适的说法是难以更新。

我搜了全网都找不到一个比较详细的解答，所以我自己画了一张图详细讲述一下是难以更新参数是怎么回事。
首先要明确，这个问题和Fast R-CNN的采样方法息息相关，这个问题直接指导了Fast R-CNN在训练时对一个mini-batch的采样方法。
我画了一张图，对比了Fast-R-CNN和SPPnet的训练差异：

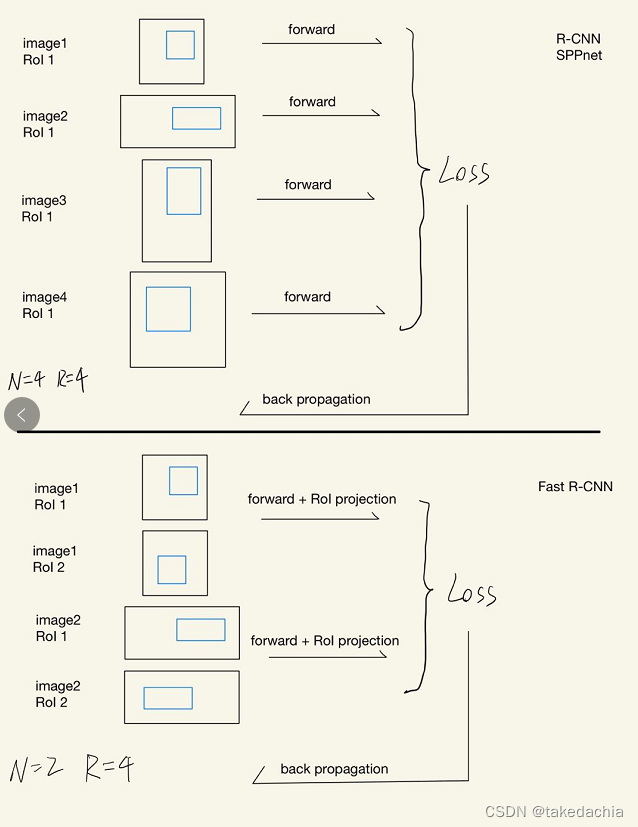
上半部分是SPPnet/R-CNN的训练流程。假设我们的batch_size设为4，根据平均采样的原则，一般是4张图片中各自的候选框进入前向传播，由于是4张不同的图片，所以我们需要经过4次正向传播。然后算出Loss，再进行反向传播。
下半部分是Fast R-CNN的训练流程。我们依然设batch_size为4，但我们使用了分层抽样的原则。因为每个图片都有2000个候选框，所以我们先抽取若干张图片，再在每张图片中抽取多个候选框。比如我们抽取2张图片（N=2），每张图片抽取2个候选框。这样的话对于Fast R-CNN每个图片只需要经过一次正向传播，对于候选框按位置进行映射抠图即可，在这个例子中我们只需要2次正向传播就能行。

如果把batch_size放大到128，我们假设每个mini-batch只抽取2张图片，每张图片各自抽64个候选框，那么我们只需要2次正向传播就能扫完一个批次。
但是SPPnet/R-CNN则要128次正向传播，这样对算力的要求急剧增加。所以对于fine tuning来说，这是不效率的。

这就是为什么SPPnet训练时难以更新卷积网络的权重的原因，并不是无法跟新，而是非常低效。

---

所以，文中作者采用的mini-batch采样策略为：
先随机采样2张图片，每张图片采样64个候选框，batch_size共计128。
这128个样本中，25%为正样本，其余为负样本（这个和R-CNN一样）。
其中，IoU大于0.5为正样本，IoU在0.1到0.5之间的为负样本。
此外，对IoU小于0.1的样本采用难例挖掘的策略（hard example mining）来训练。我的理解是，因为IoU小于0.1的样本数量非常多，所以值得挖掘，训练时对目标框IoU<0.1的样本进行预测，如预测有误就加入hard example错题集进入下一轮的训练。
此外，作者还使用了0.5概率的水平翻转作为数据增强的手段。

多任务的损失函数

Fast R-CNN网络最后有两个输出，分别是softmax分类和bbox回归器，所以这是一个多目标优化问题。
对于这个两个目标的优化问题，作者的思路是将两个设计好的损失函数进行加和，把两个目标的优化问题简化成单目标优化问题。

Fast R-CNN中，每个样本（候选框）都会输出：
一个离散概率分布 $p=\left(p_0,\dots ,p_K\right)$，包含了k+1个类别的预测概率
一组回归系数 $t^k=\left(t_{\mathrm{x}}^k,t_{\mathrm{y}}^k,t_{\mathrm{w}}^k,t_{\mathrm{h}}^k\right)$，$k$对应各个分类。

（注：对于回归系数和Bounding box regression，详细可见我这篇文章。）

每一轮的训练中，一个候选框都会有一个Ground-Truth相关的类别标签（记为类别号$u$，其中0为背景类）；还有一个基于Ground-Truth算出来的一组回归系数$v$。
因为有了类别标签，我们的回归系数$t^k$只需要关注$u$类别的，因此我们只需要 $t^u$。
如下图，这样就可以对每个候选框分别计算softmax和回归器的Loss了。

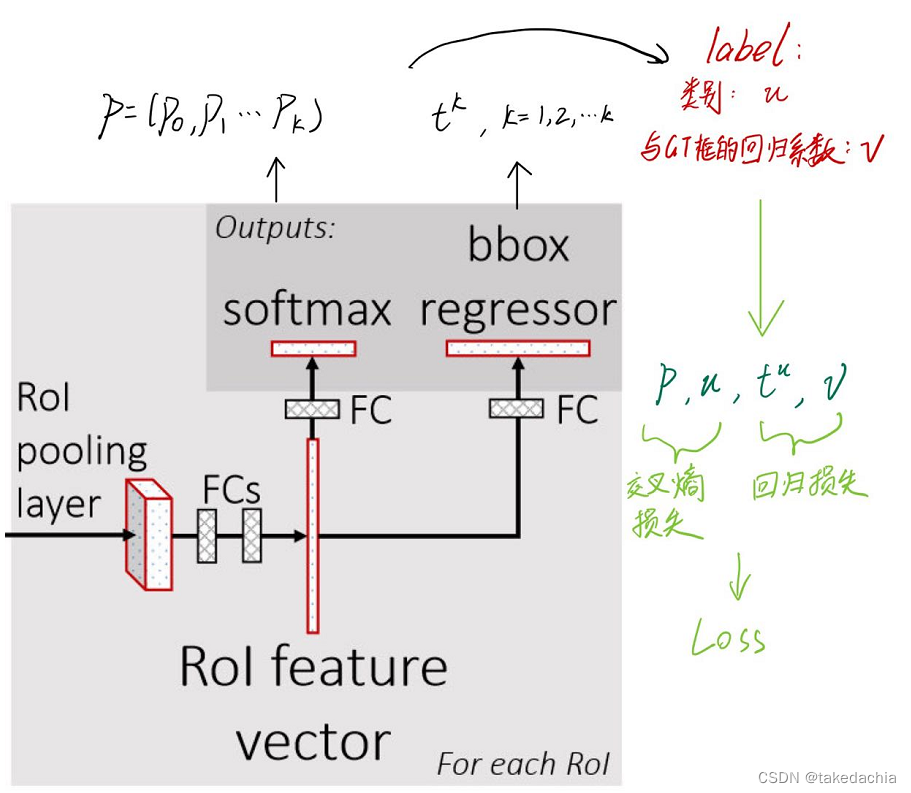
我们的目的是设计出softmax和回归器各自的Loss后，加和后能成为一个单目标的优化问题，这样一个多任务损失函数能正常优化。

作者设计的损失函数为：
$$L\left(p,u,t^u,v\right)=L_{\mathrm{cls}}(p,u)+\lambda [u\ge 1]L_{\mathrm{loc}}\left(t^u,v\right)$$

损失函数第一项即分类损失$L_{\mathrm{cls}}$，为交叉熵损失函数。由于只有第$u$项的真实概率为1，所以交叉熵损失函数项直接可直接等价成：
$L_{\mathrm{cls}}(p,u)=-\log p_u$
$p_u$为第$u$项的概率，即对第$u$项的预测概率取对数损失即可。

---

损失函数第二项是定位系数的回归器损失$L_{\mathrm{loc}}$，作者这里采用了 ${\mathrm{smooth}}_{L_1}$ 损失函数。表示为：
L l o c ( t u , v ) = ∑ i ∈ { x , y , w , h } smooth ⁡ L 1 ( t i u − v i ) L_{\mathrm{loc}}\left(t^{u}, v\right)=\sum_{i \in\{\mathrm{x}, \mathrm{y}, \mathrm{w}, \mathrm{h}\}} \operatorname{smooth}_{L_{1}}\left(t_{i}^{u}-v_{i}\right) Lloc​(tu,v)=i∈{x,y,w,h}∑​smoothL1​​(tiu​−vi​)
暂先不管${\mathrm{smooth}}_{L_1}$。对于一个候选框样本，它有一个定位信息$i$，它相对于类别$u$的GT框会产生一个真实的偏移系数$v_i$，还会根据回归器预测出一个偏移系数$t_i^u$，从它俩之间构建损失函数。

在R-CNN的bbox回归问题中（详见我这篇文章），回归器的损失函数是平方和，即$L_2$损失函数，它可以求得参数的解析解。

但是，Fast R-CNN中，我们需要同时优化两个任务（分类+定位）以构建端到端的训练，并且使用两者加和的方式转化为单目标优化问题。如果使用$L_2$损失，一旦$t_i^u$和$v_i$相差过大，因为平方项的关系，Loss值会非常大，可能会大交叉熵的Loss几个数量级。这样可能会造成学习困难，所以两个任务的Loss最好保持在一个量度上。
但是如果使用$L_1$损失的话，零点处又难以求导。所以作者采用了${\mathrm{smooth}}_{L_1}$ 损失函数，在靠近0的区间范围内（$[-1,1]$），函数变成弯曲的形状便于求导。三者的函数图像如下图所示：

${\mathrm{smooth}}_{L_1}$写成函数表达如下：
smooth ⁡ L 1 ( x ) = { 0.5 x 2  if  ∣ x ∣ < 1 ∣ x ∣ − 0.5  otherwise  \operatorname{smooth}_{L_{1}}(x)=

smoothL1​​(x)={0.5x2∣x∣−0.5​ if ∣x∣<1 otherwise ​

作者在论文中也提到，Smooth L1损失相较于L2对远端值不敏感。如果回归的范围没有限制，使用L2损失就需要仔细调学习率以防梯度爆炸。

最后，$L_{\mathrm{loc}}$前面的$[u\ge 1]$项表示，类别号在大于等于1时，这个项为1。如$u=0$，即为背景类时，这个项等于0，即不计算回归损失。
再前面的$\lambda$是加和系数，是超参数，作者认为将其设为1可平衡两个Loss任务。

---

综上，损失函数的设计将Fast R-CNN的训练变成了单阶段的训练，训练效率大大提升。
这是相较于R-CNN、SPPnet的一大创新点。

关于 RoI pooling 层的梯度反传

论文这部分讲到了一个训练时的细节，即RoI pooling是怎么进行梯度反传的？

---

因为RoI pooling是一类Max pooling，我们先要知道Max pooling是怎么反向传播梯度的：

上图中我们对一张4×4的feature map做大小为2×2，步长为2的最大池化，得到一个2×2的output。并且这4个输出值$y_1,y_2,y_3,y_4$应当带上它在原feature map中的位置信息，即$x_6,x_8,x_9,x_{16}$）。
对这个output求导后，各个位置的梯度大小应该反向赋给原feature map的对应位置，然后其余位置梯度都是0。
这就是max pooling的反向传梯度的过程。

在实际问题中，我们经常会碰到池化核区域重叠的情况，即步长＜尺寸。
当上一个池化核扫到的最大值 和 下一个扫到的最大值都是同一个位置的数，都位于重叠区域时，梯度又该怎么算呢？
如下图。
我们在算$x_4$处的梯度应当是最后$y_1,y_2$两处偏导数的和，因为它们对应的原feature map的位置是同一个。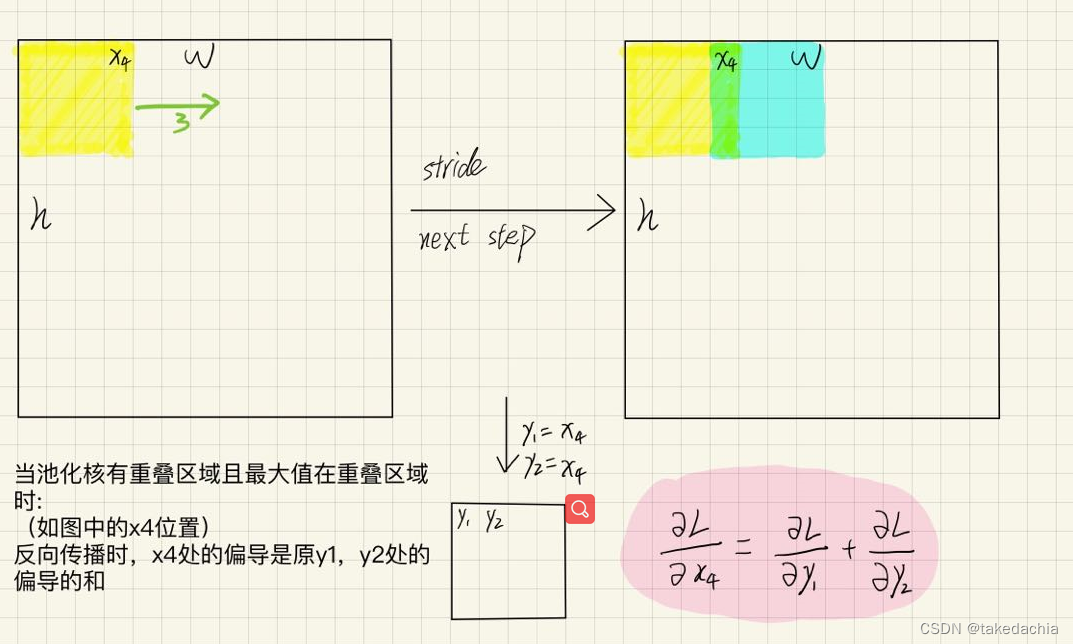

---

在RoI pooling中，梯度的反传和上面讲到的Max pooling机制是一样的。
有一点新的不同就是，Fast R-CNN训练时传入的一个mini-batch是从2张图片中各随机选取的64候选框。
我们以1张图片抽取64个候选框为例，我们需要在1张图片生成的conv feature map上抠出大大小小64张小feature map，再传入RoI pooling层。所以这些小feature map的位置一定会有重叠的情况，如果我们的max pooling取到的最大值恰好在重叠区域又怎么办呢？

见下图：

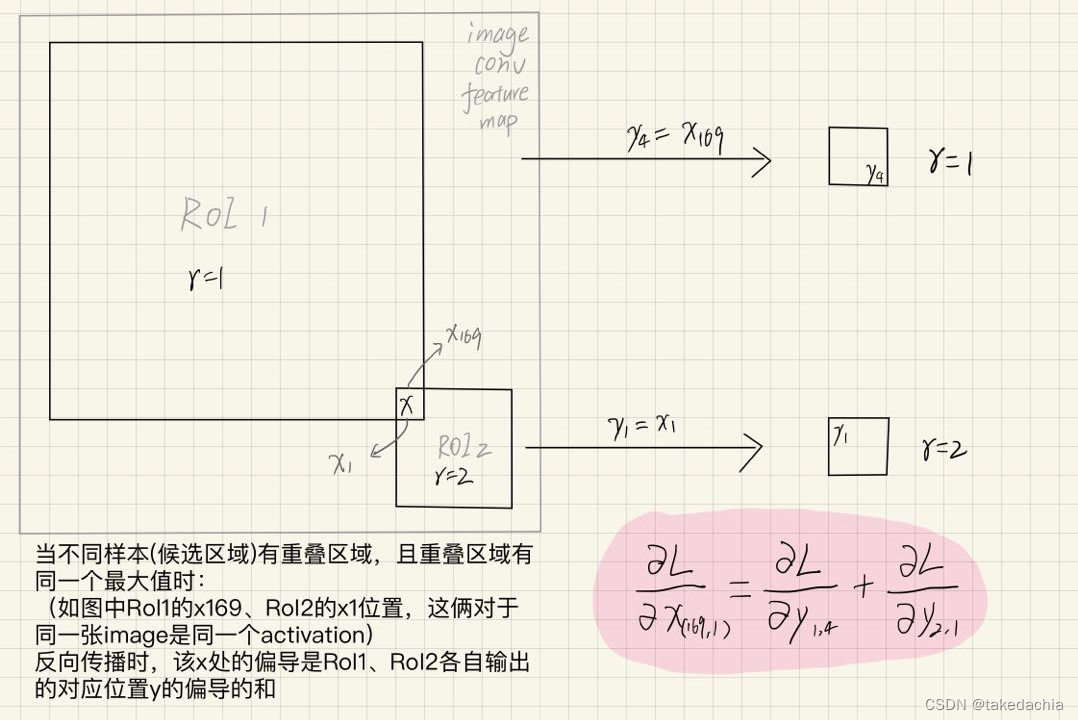
一张图片的conv feature map中有2个候选框映射，它们各自需要输出2×2的output。
假设它们之间如图位置有一重合处（对于框1为$x_{169}$；对于框2为$x_1$），在各自max pooling后都选取了这个数作为对于位置的输出（框1输出在$y_4$，框2输出在$y_1$）。
本质上这是来自同一个位置的$x$，那么此处的偏导也是框1、框2各自输出的对应位置$y$的偏导的和。

所以，在Fast R-CNN的RoI pooling层中，对一个输入的$x$位置求偏导经历了两次加和，如output之间存在同源最大值，反向传播时就需要在源位置将梯度加和。

故论文中这个难懂的公式讲的就是上面这个意思，只要懂这个公式在做一件什么事即可：
$$\frac{\partial L}{\partial x_i}=\sum _r\sum _j\left[i=i^{\ast }(r,j)\right]\frac{\partial L}{\partial y_{rj}}$$

关于尺度不变性

尺度不变性是目标检测模型的一个评估指标。
如果给你一张经过缩放的大图和小图，模型都能辨别出图片中有一匹马，马上骑着一个人的话，那么模型的尺度不变性比较好。

提高模型的尺度不变性，可以在训练时将所有图片固定在一个尺寸，测试时也使用同一个尺寸，我们的目标是让模型自己去学习其中的尺度不变性。这称为单尺度目标检测。
此外，还可以将图片在训练时随机缩放成1种预设的尺寸进行训练，这也是一种数据增强的方法。在测试时，将图片缩放成所有预设的尺寸，形成一个“图像金字塔”，对每个尺寸下的生成的候选框进行尺度归一化。这称为多尺度目标检测。

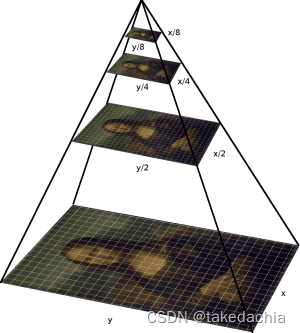
论文后面（试验结果2部分）作者会做一些实验来探索尺度不变性。

模型的测试细节

模型fine tuning训练好后，就可以进行测试环节了。
在对一张图片进行测试前，一样需要随机生成（通过selective search）大约2000个候选框的位置信息。
然后进入前向计算，之后会对结果用非极大值抑制算法处理多余的候选框（和R-CNN一样）。

利用 截断性的SVD 加速推理

我们知道在Fast R-CNN模型的最后存在着大量的全连接层，如下图。

我们知道Fast R-CNN传入一张图片后，仅需要在CNN网络进行1次前向计算，再通过RoI project投影出对应的feature map，进入RoI池化。然后，输出的每一个特征向量（约2000个）都会经历一次全连接层的前向运算，再进入softmax和bbox regression。

故测试时的全连接层运算量远大于训练时。
作者指出，事实上测试时大量的算力都会耗费在全连接层的计算上。
我们知道全连接层的计算都是矩阵运算，对于一个矩阵$W$，我们可以对其进行奇异值分解（SVD），将一个臃肿的矩阵简化成三个矩阵的乘积，我们可以对三个矩阵进行“瘦身”，取奇异值大小排名靠前的对应部分组成新的矩阵，且几乎不损耗原矩阵$W$的信息：
$$W\approx U{\Sigma }_t{V}^T$$
经过瘦身的矩阵运算速度将会大大提升。具体提升多少见后面的实验结果部分。
（SVD这部分具体知识细节可参考线性代数）

实验结果1

模型的以下3项主要实验结果支持了Fast R-CNN的贡献：

• 在VOC2007、2010、2012数据集上有出色的精度
• 比R-CNN、SPPnet更快的训练、测试速度
• 使用主干网络为VGG-16模型时，微调卷积层的权重提升了检测精度

实验中作者主要使用了三种CNN模型作为Fast R-CNN的主干网络。
将以AlexNet为主干网络的模型称为S模型（small）；
将以VGG_CNN_M_1024为主干网络的模型称为M模型（medium），它与S模型同深度，但更宽；
将以VGG-16为主干网络的模型称为L模型（largest），是最大的模型。

在VOC数据集上的结果

下面3张表依次是VOC2007、2010、2012上的结果，并细分到了各个类别的精度。所有模型的主干网络都使用了VGG-16（即L模型）。
可以看到Fast R-CNN（文中的FRCN [ours]）的总体精度是最高的。可以粗略看到右下角的mAP值都比上面的要高。

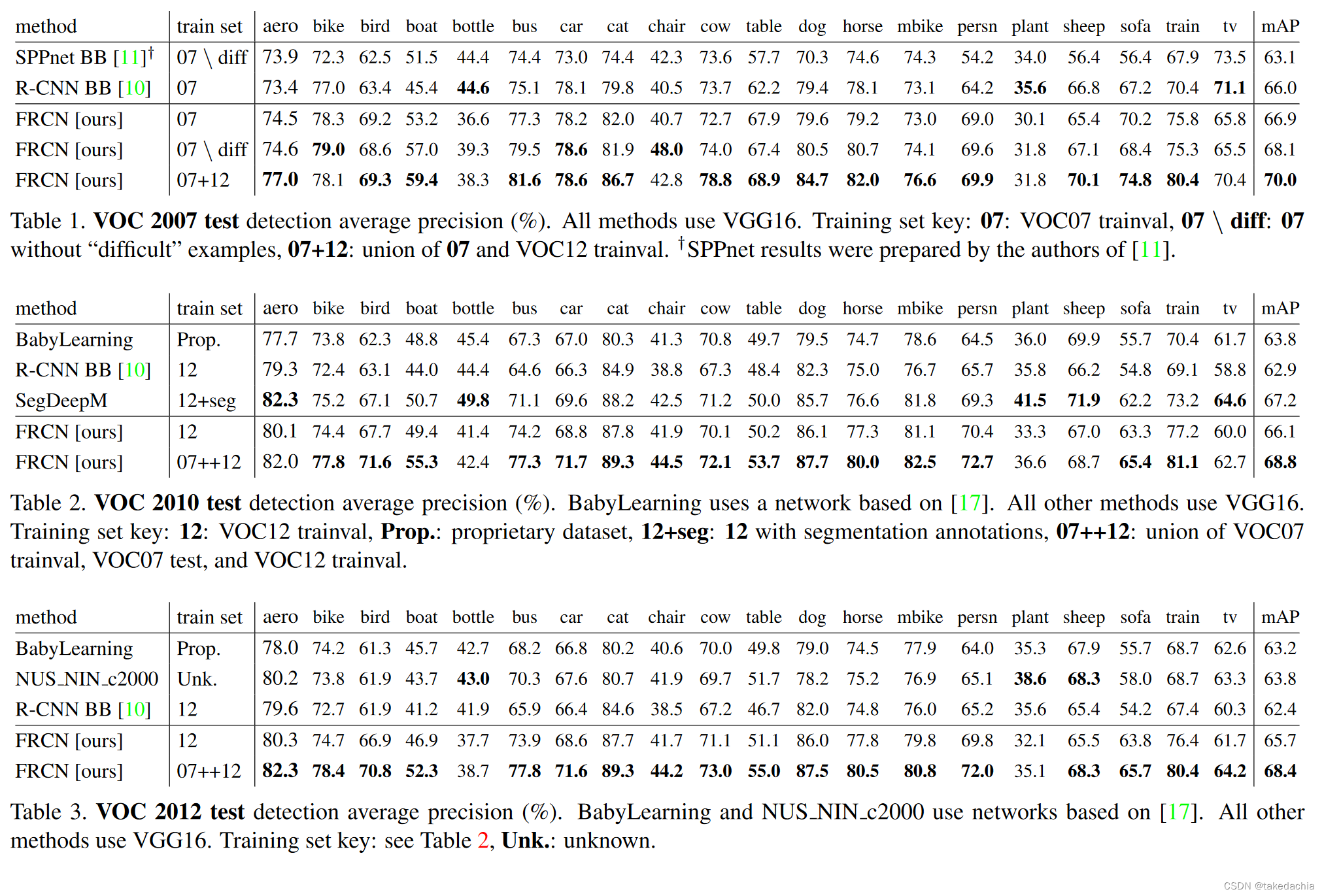
训练和测试速度的提升

作者做了下表，展示了 Fast R-CNN 、R-CNN、SPPnet的训练、测试时长比较。3类不同大小的模型都进行了比较。
可以看到在S模型中，Fast R-CNN的训练速度比R-CNN快了18.3倍。
在L模型中，测试速度快了146倍；如果测试时使用前面提到的SVD技术，速度提升了213倍。同时精度是最高的。

这里作者就指出测试时使用了SVD会提速30%多，但精度只下降了0.3%。
并且SVD是个单独的trick，不需要进行事后的再fine tuning。

fine-fune 卷积层的权重提升检测精度

如前所述，SPPnet难以更新模型权重，所以当时SPPnet使用了冻结全连接层之前所有层权重的方法，以提高效率，并且准确率也还不错。
但作者认为，前面卷积层的参数也很重要，fine-tune卷积可提升模型精度。
于是作者用L模型做了冻结层参数的实验，证明了这个结论。

下图显示，微调全连接层fc6的精度不如微调卷积层conv3_1、conv2_1的精度，微调的层越深，效果越好。

但是不是所有的卷积层都有必要被fine-tune呢？作者认为也不一定。
作者发现在更小的模型中（如S模型和M模型），微调第一个卷积层conv1对精度没什么影响，反而让模型训练效率下降（比如需要更大的GPU显存）。从第二个卷积层开始微调相对比较合适。

实验结果2——验证Fast R-CNN设计的有效性

作者接着就Fast R-CNN模型本身的设计，做了一些实验论证其有效性。
我觉得这是非常值得学习的科研思路，不仅需要对一个新方法的结果和老方法进行对比论证，还需要对它的新的设计论证其科学性，更好地解释论证新方法的科学价值。

多任务训练真的有用吗？

我们知道R-CNN和SPPnet使用了多任务训练的方法，对一个模型分别训练1个CNN模型用于提取特征、1个线性SVM分类器用于候选框图像分类、1个bbox回归器用于调整框的定位。
而Fast R-CNN设计了一个损失函数将多任务优化成了单任务，优化一个损失函数一步到位进行训练。这样降低了训练资源消耗，提升了效率。

但是多任务训练是否真的提升了模型的精度呢？作者设计了实验，在Fast R-CNN模型上，人工将这3个任务（特征提取、分类、回归）各自分开、组合训练，进行对比。
下图左边依次是 多任务训练、单阶段训练、测试时使用bbox回归，打上勾的为训练测试的组合。
而第一列我用黑框框出来(即都没有打勾)的表示只使用图像分类（交叉熵损失）进行训练得到的结果。
实验结果用VOC07数据集上的mAP表示。

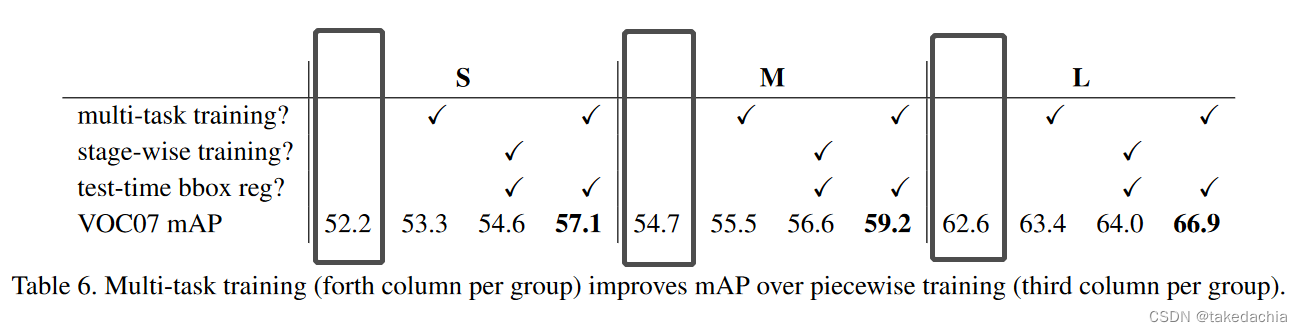
可以看到使用多任务训练+bbox回归是精度提升最高的。证明多任务训练是work的。

关于尺度不变性

前面介绍了两种关于尺度不变性的目标检测策略。
作者做了实验来对比两种策略的结果，对比了两者的性能和精度差异。

下图scales中：1表示单尺度策略（都缩放成600像素大小），5表示多尺度策略（有480、576、688、864、1200五种预设尺度）。

可看到多尺度策略下检测精度比单尺度高一点，但是单尺度检测速率比多尺度要快很多。
所以看上去单尺度性价比高，实际情况下需要进行取舍。

是否需要更多的训练数据

作者看到传统的目标检测算法（如DPM，也是原作者自己的工作）有一个精度饱和（mAP saturate）的现象。
即训练数据到了一定程度后，模型的精度上不去了。
那么Fast R-CNN是否有这样的现象呢？

作者做实验对VOC07数据集进行了扩充，将VOC2012扩充进训练集，发现精度上升（66.9% → 70.0%）。
因此，Fast R-CNN模型在训练数据增大的时候，模型的精度也提升，没有精度饱和现象，这是一个优秀的目标检测模型应有的特性。

SVM分类器 vs softmax

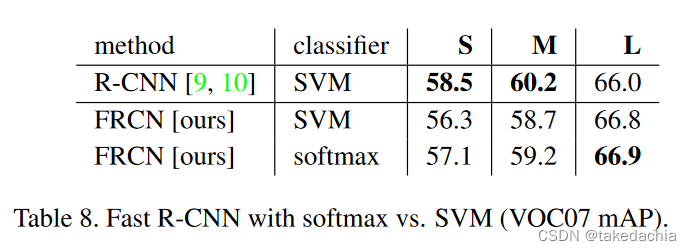
我们知道R-CNN和SPPnet使用了SVM分类器对候选框进行图像分类。
但Fast R-CNN设计成了softmax分类，这和整个模型的设计目的有关，为了进行多任务训练以及模型的fine-tuning。

就分类效果上，SVM和softmax相比又如何呢？作者做了如下实验。

我们发现在Fast R-CNN中，softmax比SVM更有用。
并且虽然在小模型上R-CNN中的SVM精度高一点，但随着模型增大，softmax依然是最有用的那一个。
考虑到多任务训练的效率等因素，softmax是优于SVM的。

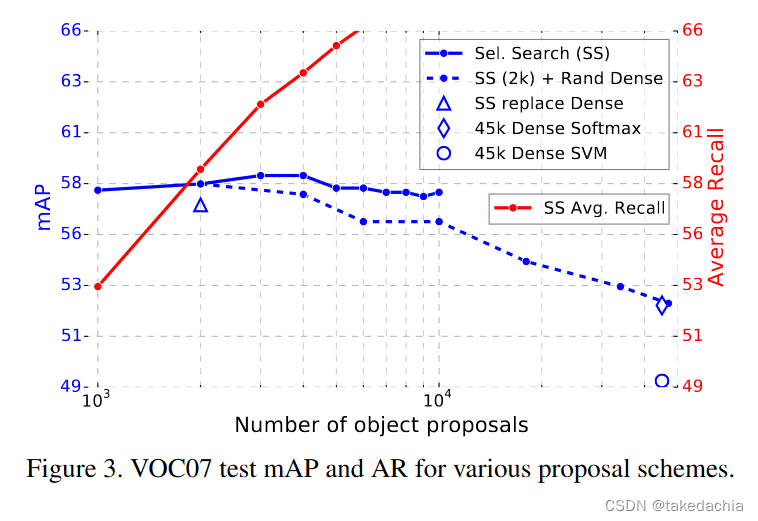
候选框越多越好吗？

目前主要有两种框生成算法，一种是生成比较稀疏分布的selective search，一种是基于DPM的生成稠密候选框的算法。

简单看一下下面这张图，可看到使用了selective search（图中蓝色实线）随着候选框数量增多，精度也会发生波动，所以并不是候选框越多越好。
使用了selective search+随机生成稠密框的组合算法，随着框数量增加，精度大幅下降。

（完）