动态规划 | 01背包问题例题 | 分割等和子集、石头相撞、目标和、1和0 | leecode刷题笔记

跟随carl代码随想录刷题
语言：python

---

416. 中等分割等和子集

题目：给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。
👉示例 1：
输入：nums = [1,5,11,5]
输出：true
解释：数组可以分割成 [1, 5, 5] 和 [11] 。
👉示例 2：
输入：nums = [1,2,3,5]
输出：false
解释：数组不能分割成两个元素和相等的子集。

题目分析——01背包

01背包：一个物品只能放一次（一个元素只能用一次）
完全背包：一个物品可以放多次（一个元素可以用多次）

由题目：将数组分割成两个子集，两个子集的元素和相等
可得：每个子集的元素和为总和 / 2
分析：

• 如果总和sum为奇数，则无法划分两个元素和相等的数组，因此一定不存在return False
• 每个子集的元素和为sum(数组) / 2，相当于背包容量
• 子集中的元素相当于物品
• 最终求出的dp数组中，最大值即为背包所能容纳的元素和。如果元素和 == 背包容量，则return True，否则return False。

五部曲

1. 确定dp数组以及下标的含义
   • dp[j]表示：容量为j的背包，所背的物品价值最大可以是dp[j]
   • 即：总和为j的子集，所包含的元素总和最大可以是dp[j]
2. 确定递推公式
   • 背包的递推公式是：dp[j] = max(dp[j], dp[j - item_weight[i]] + item_value[i])
   • 即：dp[j] = max(dp[j], dp[j - nums[i]] + nums[i])
3. dp数组初始化
   • 如果题目所给数组元素为正整数，则dp数组初始化为0
   • 如果题目所给数组元素有负数，那么dp数组初始化为负无穷-float(inf)
   • 要保证一点：递归时由元素覆盖初始值，而不是被初始值所覆盖。
     • 因此本题初始化为0：dp = [0] * (sum_ + 1)
4. 确定遍历顺序
   • 外层：元素遍历
   • 内层：range(数组总和, 元素-1， -1) # 逆序遍历
5. 举例推导dp数组
   • 如果dp数组的最后一个元素值 == 背包容量，说明存在元素总和为sum_的子集，return True
   • eg：
     • nums = [1,5,11,5]
     • sum_ = (1+5+11+5)/2 = 11
     • dp数组：[0, 1, 1, 1, 1, 5, 6, 6, 6, 6, 10, 11]
     • 可以看到：dp数组最后一个元素等于sum_，因此return True

完整代码如下

class Solution:
    def canPartition(self, nums: List[int]) -> bool:
        target = sum(nums)
        if target % 2 == 1:
            return False
        # 背包容量
        target = target//2
        # 初始化dp数组
        dp = [0] * (target + 1)
       
        # 物品重量
        for i in range(len(nums)):
            for j in range(target, nums[i]-1, -1):
                dp[j] = max(dp[j], nums[i] + dp[j - nums[i]])
                # print(dp)
                if dp[j] == target:
                    return True
        
        return False
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

473. 中等火柴拼正方形

题目：你将得到一个整数数组 matchsticks ，其中 matchsticks[i] 是第 i 个火柴棒的长度。你要用 所有的火柴棍 拼成一个正方形。你 不能折断 任何一根火柴棒，但你可以把它们连在一起，而且每根火柴棒必须 使用一次 。
如果你能使这个正方形，则返回 true ，否则返回 false 。
👉示例1：

输入: matchsticks = [1,1,2,2,2]
输出: true
解释: 能拼成一个边长为2的正方形，每边两根火柴。
👉示例 2:
输入: matchsticks = [3,3,3,3,4]
输出: false
解释: 不能用所有火柴拼成一个正方形。

698. 中等划分为k个相等的子集

题目：给定一个整数数组 nums 和一个正整数 k，找出是否有可能把这个数组分成 k 个非空子集，其总和都相等。
👉示例 1：
输入： nums = [4, 3, 2, 3, 5, 2, 1], k = 4
输出： True
说明： 有可能将其分成 4 个子集（5），（1,4），（2,3），（2,3）等于总和。
👉示例 2:
输入: nums = [1,2,3,4], k = 3
输出: false

完全背包：一个物品可以放多次（一个元素可以用多次）

1049. 最后一块石头的重量 II

题目：有一堆石头，用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：
如果 x == y，那么两块石头都会被完全粉碎；
如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。
最后，最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下，就返回 0。
示例 1：
输入：stones = [2,7,4,1,8,1]
输出：1
解释：
组合 2 和 4，得到 2，所以数组转化为 [2,7,1,8,1]，
组合 7 和 8，得到 1，所以数组转化为 [2,1,1,1]，
组合 2 和 1，得到 1，所以数组转化为 [1,1,1]，
组合 1 和 1，得到 0，所以数组转化为 [1]，这就是最优值。
示例 2：
输入：stones = [31,26,33,21,40]
输出：5

题目分析

将石头尽量分成重量相等的两堆，这样相撞之后剩余的重量最小。

动态规划五部曲

1. 确定dp数组以及下标的含义
   • dp[j]表示容量为j的背包，即最多可以背dp[j]这么重的石头
2. 递推公式
   • dp[j] = max(dp[j], dp[i - weight[i]] + value[i])
   • dp[j] = max(dp[j], dp[j - stones[i]] + stones[i])
3. dp数组如何初始化
   • dp数组开到石头数量的一半就行。
   • dp = [0] * 15001
4. 确定遍历顺序
   • 外层是物品的遍历，即：石头的遍历for i in range(len(stones)):
   • 内层是背包的倒序遍历：for j in range(target, stone[i]-1, -1):
5. 举例推导dp数组
   • 找出dp数组的最大值，即为当前这堆石头的重量
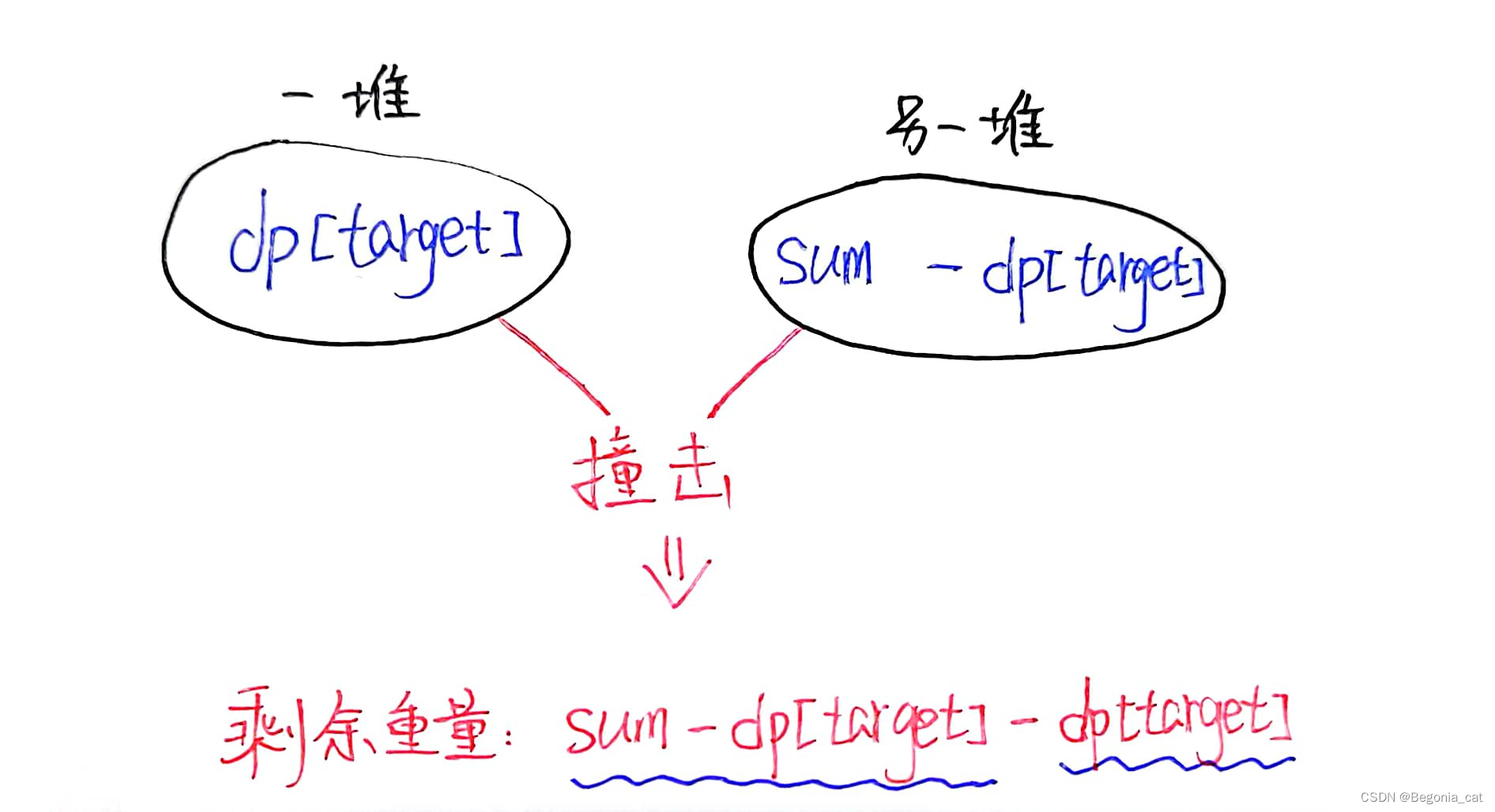
   • 用sum - target得到另一堆石头的重量
   • 相撞之后剩下的最小石头重量是(sum - dp[target]) - dp[target]
     • 🙋问什么是(sum - dp[target]) - dp[target]，而不是dp[target] - (sum - dp[target])？
     • 因为target = sum / 2，是向下取整，所以target是≤中值的，所以target是≤(sum - dp[target])的。
       

完整代码如下

class Solution:
    def lastStoneWeightII(self, stones: List[int]) -> int:
        target = sum(stones) // 2
        # 初始化dp
        dp = [0] * (target + 1)

        for i in range(len(stones)):
            for j in range(target, stones[i]-1, -1):
                dp[j] = max(dp[j], dp[j - stones[i]] + stones[i])
        return sum(stones) - dp[target] - dp[target]
1
2
3
4
5
6
7
8
9
10

474. 一和零

题目：给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的长度，该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的 子集 。
👉示例 1：
输入：strs = [“10”, “0001”, “111001”, “1”, “0”], m = 5, n = 3
输出：4
解释：最多有 5 个 0 和 3 个 1 的最大子集是 {“10”,“0001”,“1”,“0”} ，因此答案是 4 。
其他满足题意但较小的子集包括 {“0001”,“1”} 和 {“10”,“1”,“0”} 。{“111001”} 不满足题意，因为它含 4 个 1 ，大于 n 的值 3 。
👉示例 2：
输入：strs = [“10”, “0”, “1”], m = 1, n = 1
输出：2
解释：最大的子集是 {“0”, “1”} ，所以答案是 2 。

题目分析

本题是两个维度的01背包问题。

动态规划五部曲

1. 确定dp数组以及下标的含义
   • dp[i][j]：最多有m个0和n个1的strs的最大子集的大小为dp[i][j]
2. 确定递推公式
   • dp[i][j]可以由前一个strs里的字符串推导出来，strs里的字符串有zeroNum个0，oneNum个1。
   • dp[i][j]可以是dp[i - zeroNum][j - oneNum] + 1
   • dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1)。
   • 字符串的oneNum和zeroNum相当于物品的重量weight[i]，字符串本身的个数相当于物品的价值value[i]
3. dp数组如何初始化
   • 因为物品的价值不会是负数，因此初始为0，可以保证递推的时候，dp[i][j]不会被初始值覆盖。
4. 确定遍历顺序
   • 物品（即strs数组中的各个str）放在外循环，在这个过程中要统计一下当前字符串的0的数量和1的数量。
   • 背包容量range(m, zeros - 1, -1)，range(n, ones - 1, -1)放在内循环，从前往后遍历。可以看到这里背包是二维的，有两层遍历。

5. 举例推导dp数组

完整代码如下

class Solution:
    def findMaxForm(self, strs: List[str], m: int, n: int) -> int:
        # 初始化
        dp = [[0 for _ in range(n + 1)] for _ in range(m + 1)]

        # 遍历
        for str in strs:
            ones = str.count('1')  # 关键
            zeros = str.count('0')  # 关键
            for i in range(m, zeros - 1, -1):
                for j in range(n, ones - 1, -1):
                    dp[i][j] = max(dp[i][j], dp[i - zeros][j - ones] + 1)
        return dp[m][n]  # 注意返回值
1
2
3
4
5
6
7
8
9
10
11
12
13