前言💬

本篇博客则主要介绍二叉树的基础操作；然而标题虽然是二叉树但是本篇博客只会涉及部分完全二叉树的内容，将会在下一篇博客中介绍完全二叉树也就是堆的相关操作！

在上一篇博客中也已经详细介绍了二叉树的概念理论等，本文将不再对其进行论述，而利用的二叉树的相关理论不清楚的话，可以移步至数据结构----树及二叉树这篇博客中进行了解！

1.二叉树的链式存储

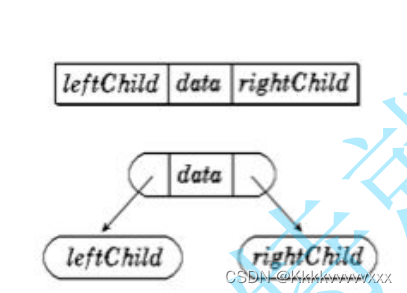
二叉树的链式存储结构是指，用链表来表示一棵二叉树，即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成，数据域和左右指针域，左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。

用一张图片对于上述进行一个直观地解释：

用代码进行编写，格式如下

typedef int  TreeNodeType;
typedef struct TreeNode
{
	TreeNodeType data;
	struct TreeNode* left;
	struct TreeNode* right;
}TreeNode;
1
2
3
4
5
6
7

在了解到二叉树的结构方式定义之后，下来我将建设一个简单二叉树以供后续操作的进行：

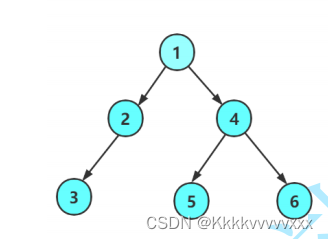
int main()
{
	TreeNode* n1 = (TreeNode*)malloc(sizeof(TreeNode));
	TreeNode* n2 = (TreeNode*)malloc(sizeof(TreeNode));
	TreeNode* n3 = (TreeNode*)malloc(sizeof(TreeNode));
	TreeNode* n4 = (TreeNode*)malloc(sizeof(TreeNode));
	TreeNode* n5 = (TreeNode*)malloc(sizeof(TreeNode));
	TreeNode* n6 = (TreeNode*)malloc(sizeof(TreeNode));

	n1->data = 1;
	n2->data = 2;
	n3->data = 3;
	n4->data = 4;
	n5->data = 5;
	n6->data = 6;
	n1->left = n2;
	n1->right = n4;
	n2->left = n3;
	n2->right = NULL;
	n3->left = n3->right = NULL;
	n4->left = n5;
	n4->right = n6;
	n5->left = n5->right = NULL;
	n6->left = n6->right = NULL;

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

2.遍历

2.1前序遍历

前序遍历：访问根节点的操作发生于遍历其左右子树之前；简单来说就是先访问根节点，在访问左子树，最后访问右子树；

前序遍历代码如下：

void PrevOrder(TreeNode* root)
{
	if (root == NULL)
	{
		printf("NULL");
		return;
	}
	printf("%d ", root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);
}
1
2
3
4
5
6
7
8
9
10
11

代码看起来十分简单，但是其这个递归过程相对而言是比较麻烦的，在下图我会将其递归过程中调用的逻辑关系进行表示以供参考！

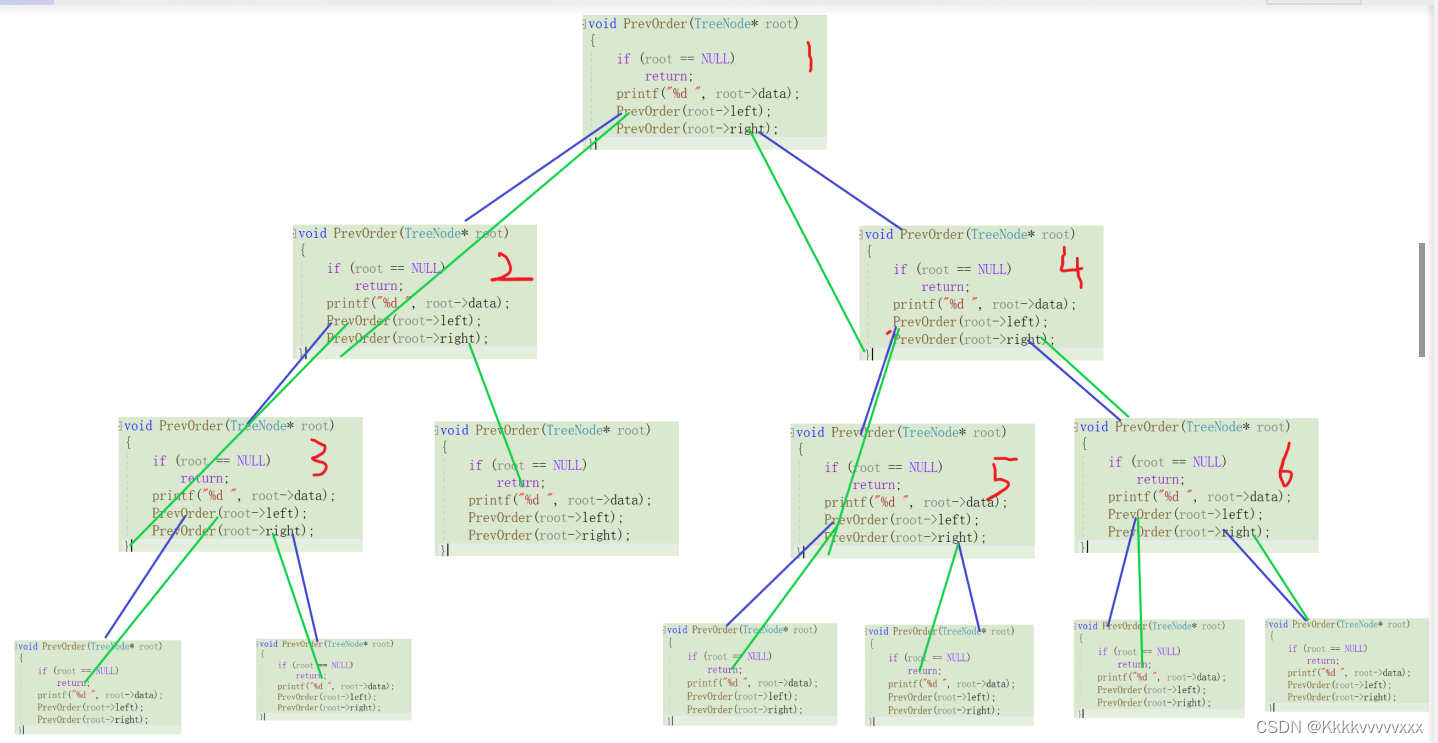
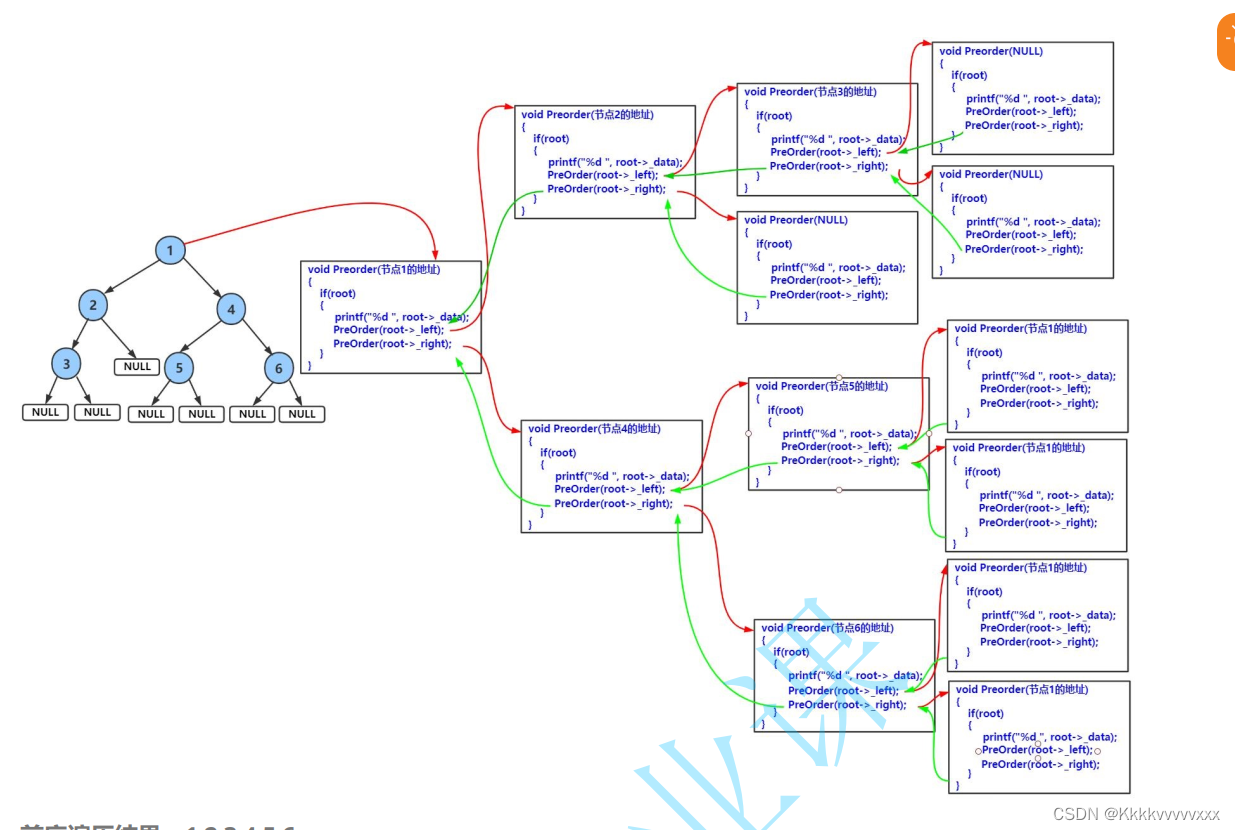
分析：在递归调用过程成，会先打印根节点然后取遍历左子树，左子树遍历完成后才会去遍历右子树，其函数调用关系如图所示；关于这部分内容我录制了个视频也可以转过去查看：二叉树的前序遍历

2.2中序遍历

中序遍历：访问根节点的操作发生于遍历其左右子树之中；简单来说就是先访问左子树，在访问根节点，最后访问右子树；

void MidOrder(TreeNode* root)
{
	if (root == NULL)
	{
		printf("NULL");
		return;
	}
	MidOrder(root->left);
	printf("%d ", root->data);
	MidOrder(root->right);
}
1
2
3
4
5
6
7
8
9
10
11

关于中序遍历的视频请点击链接跳转：二叉树的中序遍历

2.3后序遍历

后序遍历:访问根节点的操作发生于遍历其左右子树之后；

//后序遍历
void PostOrder(TreeNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->data);
}
1
2
3
4
5
6
7
8
9
10
11
12

关于中序遍历的视频请点击链接跳转：二叉树的后序遍历

3.节点的数目

3.1二叉树总结点的个数

int BinaryTreeSize(TreeNode* root)
{
	if (root == NULL)
		return 0;
	return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}
1
2
3
4
5
6

3.2二叉树叶子结点的个数

int BinaryTreeLeafSize(TreeNode* root)
{
	if (root == NULL)
		return 0;
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
1
2
3
4
5
6
7
8
9
10

3.3第K层结点的个数

int BinaryTreeLevelKSize(TreeNode* root,int k)
{
	if (root == NULL)
		return 0;
	if (k == 1)
		return 1;
	return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}
1
2
3
4
5
6
7
8

关于这三种二叉树的结点数目的介绍，同样我用视频进行了介绍，因为使用文字和图片的话篇幅过长，极为不便；链接二叉树节点数目

4.二叉树的高度（深度）

//高度
int BinaryTreeHigh(TreeNode* root)
{
	if (root == NULL)
		return 0;
	int lh = BinaryTreeHigh(root->left);
	int rh = BinaryTreeHigh(root->right);

	return lh > rh ? lh + 1 : rh + 1;
}
1
2
3
4
5
6
7
8
9
10

同样，对其进行递归操作，当不满足条件时进行相应的返回即可！

5.二叉树中寻找特定结点

TreeNode* BinaryTreeFind(TreeNode* root,TreeNodeType x)
{
	if (root == NULL)
		return NULL;
	if (x == root->data)
		return root;
	TreeNode* left = BinaryTreeFind(root->left, x);
	if (left)
		return left;
	TreeNode* right = BinaryTreeFind(root->right, x);
	if (right)
		return right;

	return NULL;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

同样是递归的思想，而唯一一点需要注意的是在此函数中是按照结点存储的数据进行查找的，而一个二叉树可能存在多个相同数值的结点，此时返回第一个即可，因此先去在左子树中寻找，如果左子树找不到再去右子树寻找，如果整个树都找不到的话就返回NULL，表示该节点不存在！

而对于寻找的这部分操作时，我们其实可以利用这个函数进行修改结点的数值，利用一个结点接收该函数的返回值，然后进行修改就可以了！！！

6.销毁

//二叉树的销毁
void BinaryTreeDestory(TreeNode* root)
{
	if (root == NULL)
		return;
	BinaryTreeDestory(root->left);
	BinaryTreeDestory(root->right);
	free(root);
}
1
2
3
4
5
6
7
8
9

7.层序遍历

除过先序中序后序遍历，还可以对二叉树进行层序遍历，顾名思义，也就是一层一层进行读取；

层序遍历：从根节点出发，首先访问第一层的结点，然后从左到右访问第二层上的节点，以此类推，从左往右，从上往下；这一过程就是层序遍历。

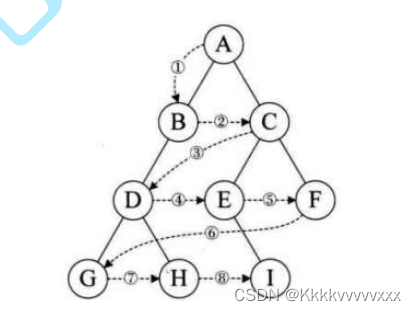
进行层序遍历时，也就是将数据一层一层进行打印，所以在进行打印之前就需要将根节点的左右子树储存起来，下一次打印时就可以直接打印左右子树了。

那该如何进行存储呢？又该如何实现这样的一个遍历打印呢？/font>

因此需要借助队列，每次将根节点的左右子树全部入队，然后将队首元素进行存储之后出队，重复这个过程就可以完成层序遍历了！

队列的实现：

#define  _CRT_SECURE_NO_WARNINGS
#include
#include
#include
#include
#include
#include

typedef int  TreeNodeType;
typedef struct TreeNode
{
	TreeNodeType data;
	struct TreeNode* left;
	struct TreeNode* right;
}TreeNode;
typedef TreeNode* QueueDataType;
typedef struct QueueNode
{
	struct QueueNode* next;
	QueueDataType data;
}QueueNode;

typedef struct Queue
{
	QueueNode* front;
	QueueNode* rear;
	int size;
}Queue;

//初始化
void InitQueue(Queue* qe);

//入队
void PushQueue(Queue* qe, QueueDataType x);

//出队
void PopQueue(Queue* qe);

//判空
bool QueueEmpty(Queue* qe);

//打印
void PrintQueue(Queue* qe);

//销毁
void DestoryQueue(Queue* qe);

//获取队列有效数据个数
int QueueSize(Queue* qe);

//获取队尾元素
QueueDataType QueueBackData(Queue* qe);

//获取队首元素
QueueDataType QueueFrontData(Queue* qe);
//初始化
void InitQueue(Queue* qe)
{
	assert(qe);
	qe->front = NULL;
	qe->rear = NULL;
	qe->size = 0;
}

//入队
void PushQueue(Queue* qe, QueueDataType x)
{
	assert(qe);
	QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));
	if (newnode == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}

	newnode->data = x;
	newnode->next = NULL;

	//链接
	if (qe->rear == NULL)
	{
		qe->front = qe->rear = newnode;
	}
	else
	{
		qe->rear->next = newnode;
		qe->rear = qe->rear->next;
		//qe->rear = newnode;
	}
	qe->size++;
}

//出队
void PopQueue(Queue* qe)
{
	assert(qe);
	assert(!QueueEmpty(qe));
	if (qe->front->next == NULL)
	{
		free(qe->front);
		qe->front = qe->rear = NULL;
	}
	else
	{
		QueueNode* del = qe->front;
		qe->front = qe->front->next;
		free(del);
		del = NULL;
	}
	qe->size--;
}



//获取队列有效数据个数
int QueueSize(Queue* qe)
{
	assert(qe);
	return qe->size;
}

//获取队尾元素
QueueDataType QueueBackData(Queue* qe)
{
	assert(qe);
	assert(!QueueEmpty(qe));
	return qe->rear->data;
}

//获取队首元素
QueueDataType QueueFrontData(Queue* qe)
{
	assert(qe);
	assert(!QueueEmpty(qe));
	return qe->front->data;
}

//判空
bool QueueEmpty(Queue* qe)
{
	assert(qe);
	return qe->front == NULL && qe->rear == NULL;
}

//打印
void PrintQueue(Queue* qe)
{
	assert(qe);
	QueueNode* cur = qe->front;
	while (cur != NULL)
	{
		printf("%d ", cur->data);
		cur = cur->next;
	}
	printf("\n");
}

//销毁
void DestoryQueue(Queue* qe)
{
	assert(qe);
	QueueNode* cur = qe->front;
	while (cur)
	{
		QueueNode* del = cur;
		cur = cur->next;
		free(del);
	}
	qe->rear = qe->front = NULL;
	qe->size = 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171

层序遍历：

//层序遍历
void LevelOrder(TreeNode* root)
{
	Queue qe;
	InitQueue(&qe);
	//将指针压入队列
	PushQueue(&qe, root);
	while (!QueueEmpty(&qe))
	{
		TreeNode* front = QueueFrontData(&qe);
		PopQueue(&qe);
		printf("%d ", front->data);

		if (front->left)
		{
			PushQueue(&qe, front->left);
		}
		if (front->right)
		{
			PushQueue(&qe, front->right);
		}
	}
	printf("\n");
	DestoryQueue(&qe);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

关于这部分文字叙述是有些苍白的，所以我在B站上录制了视频，可以跳转过去查看：二叉树的层序遍历

Ending💬

关于一般二叉树的操作也就完成了，除此之外还有完全二叉树也就是堆的操作因为篇幅原因这次并没有写出来，下一篇会对完全二叉树进行介绍，而本次博客内容中基本都是使用了递归去实现的，在不清楚其调用的逻辑关系的时候可能很难去理解这一问题，因此在搞不清时需要手画一下其函数栈帧的关系图，也就是先序遍历我所画的；

好了，就这样吧，下次见🙋‍♂️🙋‍♂️🙋‍♂️