区间素数筛

/*看了很多别人的，感觉不太全，我来补充一下nie*/

用到两个数组和欧式筛的原理

 
bool is_prime[maxn]; // 0~根号下b
bool is_prime_small[maxn];  // a~b
void segment_sieve(LL a,LL b){
	for(LL i=0;i*i<=b;i++)is_prime_small[i]=true;  //标记2~根号b之间的和数 
	for(LL i=0;i<=b-a;i++)is_prime[i]=true;        //用来标记a到b之间的和数 但却变成0~b-a
	for(LL i=2;i*i<=b;i++){        // 每一个i都两个数组都筛了，但is_prime_small是先筛的
		if(is_prime_small[i]){          
			for(LL j=2*i;j*j<=b;j+=i)is_prime_small[j]=false;  // 把i的倍数筛出去，但在2~根号b内
			for(LL j=max((LL)2,(a+i-1)/i)*i;j<=b;j+=i)is_prime[j-a]=false;//筛选a到b之间的素数 
		}
	}
}

        代码一般都是这样的，其实是欧式筛（这里不是线性筛的原因我想是因为线性筛每次都是被自己的最小质因子给筛掉的，这样的话i是很大的（可能超过根号b）,申请的空间就大了，还是会爆空间把，就拿一个偶数来举例，只会被2筛掉，此时i已经是偶数/2了）

        我当时最看不懂for(LL j=max((LL)2,(a+i-1)/i)*i;j<=b;j+=i)，这里的j的初值我看不懂

        可以这样看

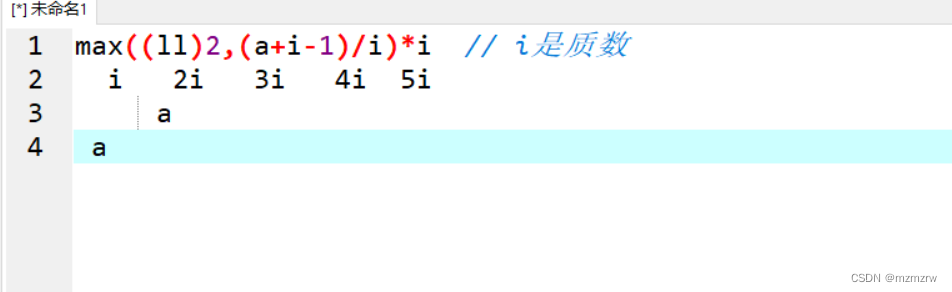
        首先这里的i是质数，2i，3i等等等都是他的倍数罢，很显然对于j,j>=a且j要尽量 小（是为了保证不漏掉），再说一点max是为了取合适的i的倍数的，还有观察(a+i-1)/i,你会发现这个值是对于上图来说a右边第一个某i的某，比如a在i~2i之间，这个值就是2（这里再乘上i那不就是上面我对j的要求吗），但有一种情况不行，当a

关于复杂度我就不说了，反正用试除法TLE，用线性筛和欧式筛爆空间（其实最开始我也是想过类似区间筛的，只是我平常都喜欢用线性筛，我就觉得不行（我是笨蛋orz））

贴个原题

The branch of mathematics called number theory is about properties of numbers. One of the areas that has captured the interest of number theoreticians for thousands of years is the question of primality. A prime number is a number that is has no proper factors (it is only evenly divisible by 1 and itself). The first prime numbers are 2,3,5,7 but they quickly become less frequent. One of the interesting questions is how dense they are in various ranges. Adjacent primes are two numbers that are both primes, but there are no other prime numbers between the adjacent primes. For example, 2,3 are the only adjacent primes that are also adjacent numbers.
Your program is given 2 numbers: L and U (1<=L< U<=2,147,483,647), and you are to find the two adjacent primes C1 and C2 (L<=C1< C2<=U) that are closest (i.e. C2-C1 is the minimum). If there are other pairs that are the same distance apart, use the first pair. You are also to find the two adjacent primes D1 and D2 (L<=D1< D2<=U) where D1 and D2 are as distant from each other as possible (again choosing the first pair if there is a tie).

Input

Each line of input will contain two positive integers, L and U, with L < U. The difference between L and U will not exceed 1,000,000.

Output

For each L and U, the output will either be the statement that there are no adjacent primes (because there are less than two primes between the two given numbers) or a line giving the two pairs of adjacent primes.

Sample

Inputcopy	Outputcopy
2 17 14 17	2,3 are closest, 7,11 are most distant. There are no adjacent primes.