树

树的基本概念

树的定义

基本术语

1. 祖先结点：从根到该节点所经分支上的所有结点，(包含父节点)。例：J的祖先结点：A、B、E
2. 子孙结点：一个结点的直接后继和间接后继(包含子节点)。例： B的子孙结点：E、F、J、K
3. 双亲结点(父结点)：一个结点的直接前驱结点
4. 孩子结点：一个结点的直接后继结点
5. 兄弟结点：同一双亲结点的孩子结点之间互称兄弟结点
6. 堂兄弟结点：父结点是兄弟关系或堂兄关系的结点
    
7. 叶子结点：度为0的结点，无后继结点，也称终端结点。
8. 分支结点：度不为0的结点，有后继结点，也称非终端结点。
    
9. 度：树中一个结点的孩子个数称为该结点的度，树中结点的最大度数称为树的度。例：A的度=3，B的度=2，树的度=3。
10. 深度：从根结点开始自顶向下逐层累加
11. 高度：从叶结点开始子底向上逐层累加
12. 层次：从根结点开始定义，根结点的层次=1。
     
13. 有序树（无序树）：树中结点各子树从左到右是有次序的，不能互换，则为有序树，否则为无序树
14. 森林：m(m $\ge$ 0)棵互不相交的树的集合
    

树的性质

二叉树

二叉树的定义

• 二叉树定义

  1. 二叉树 $\ne$度为2的树
  2. 二叉树是有序树，有左右之分

  

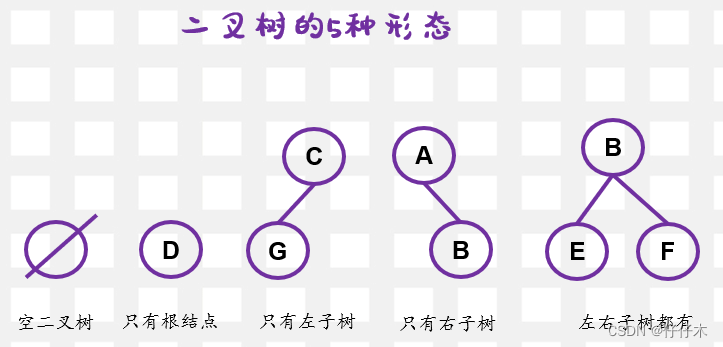
• 几种特殊的二叉树
  

  1. 满二叉树（特殊的完全二叉树）

  • 定义：一棵高度为h的，且含有​$2^h-1$ 个结点的二叉树称为满二叉树

  • 除叶子结点外，每个结点度都等于2

  • 对于编号i的结点，若有双亲结点，双亲为​$\frac{i}{2}$，左孩子​$2i$，右孩子为​$2i+1$（看上图可推）

  3. 完全二叉树

     1. 若​$i\le \frac{n}{2}$，则结点i为分支结点，否则为叶子结点。
        • 原因：第n个结点的父结点是 $\frac{n}{2}$，所以其父结点的前面都是分支结点，父结点后面都是叶子结点。
     2. 按层序编号后，一旦出现某结点（编号为i)为叶子结点或只有左孩子，则编号大于i的结点均为叶子结点。（与1意思相同）
     3. 叶子结点只可能在层次最大的两层上出现。对于最大层次中的叶子结点，都依次排列在该层最左边的位置上。
     4. 若有度为1的结点，则只可能有一个，且该结点只有左孩子而无右孩子。
     5. 若n为奇数，则每个分支结点都有左孩子和右孩子:若n为偶数，则编号最大的分支结点（编号为n/2）只有左孩子，没有右孩子，其余分支结点左、右孩子都有。
        • 左孩子​$2i$（偶数），右孩子为​$2i+1$ （奇数）

  4. 二叉排序树
     左子树上所有结点的关键字均小于根结点的关键字;右子树上的所有结点的关键字均大于根结点的关键字;左子树和右子树又各是一棵二叉排序树。

  5. 平衡二叉树
     树上任一结点的左子树和右子树的深度之差不超过1

二叉树的性质

1. 非空二叉树的叶子结点=度为2的结点+1，即​$n_0=n_2+1$。

   

2. 非空二叉树上第k层上至多有​$2^k-1$个结点($k\ge 1$)。

3. 高度为h的二叉树至多有​$2^h-1$个结点($h\ge 1$)。

4. 对于完全按从上到下、从左到右的顺序依次编号1,2,…,n，则有以下关系:

   1. 当i>1时，结点i的双亲的编号为i/2，即当i为偶数时，其双亲的编号为i/2，它是双亲的左孩子;当i为奇数时，其双亲的编号为(i-1)/2，它是双亲的右孩子。
   2. 当​$2i\le n$时，结点i的左孩子编号为2i，否则无左孩子。
   3. 当​$2i+1\le n$时，结点i的右孩子编号为2i+1，否则无右孩子.
   4. 结点i所在层次（深度）为​$lo{g}_{2}i+1$。

5. 具有n个结点的完全二叉树的高度为​$lo{g}_2(n+1)$或​$lo{g}_{2}n+1$。（要自己会推）