c++ 11:二叉树练习

分以下大纲进行讲解:

• 1.树的概念
• 2.树的深度遍历
• 3.分治算法
• 4.宽度优先
• 5.二叉树搜索树
• Trie Tree

1. 树的概念

树是一张能够分层存储数据的重要数据结构，树中的每个元素被称为树的节点，每个节点有若干个指针指向子节点。从节点角度来看，树是由唯一的起始节点引出的节点集合。这个起始节点称为根(root)。树中节点的子树目称为节点的度(degree)

在免税中，关于树的面试问题非常常见，尤其是关于二叉树，二叉树搜索树的问题。

二叉树

二叉树，是指对于树中的每个节点而言，至多有左右两个子节点，即任意节点的度小于等于2.

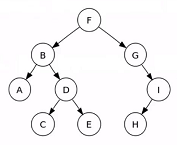
• 二叉树的第i层至多有$2^{i-1}$个子节点
• 深度为k的二叉树至多总共有$2^k-1$个节点

二叉树还可以继续分类，衍生出满二叉树和完全二叉树。

满二叉树

一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是 说，如果一个二叉树的层数为K，且结点总数是2^k-1，则它就是满二叉树。

完全二叉树

一棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为i（1≤i≤n）的结点与满二叉树中编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。

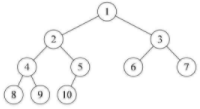
二叉树的周游

以一种特定的规律访问二叉树中的所有节点。常见的额周游方式包括：

• 前序周游(Pre-order traversal): 访问跟节点；按前序周游访问左子树；按前序周游访问右子树。也就是：跟节点->左子树->右子树
• 中序周游(In-order traversal)：按中序周游左子树;访问跟节点；按中序周游右子树。特别地，对于二叉树搜索树而言，周旭周游可以获得一个由小到大或者由大到小的有序序列。也就是：左子树>跟节点->右子树
• 后序周游(Post-order traversal):按后续周游左子树；按有序周游右子树；访问跟节点。也就是：左子树>右子树->跟节点

DFS

三种周游方式都是深度优先算法(depth - first search)

深度优先算法最自然的实现方式是通过递归实现，事实上，大部分树相关的面试问题都可以优先考虑递归。

深度优先的算法往往都可以通过使用栈数据结构将递归化为非递归实现。

层次周游

层次周游(Level traversal): 首先访问第0层，也就是根节点所在的层；当第i层的所有节点访问完之后后，再从左至右依次访问第i+1层的各个节点

层次周游属于广度优先算法(breadth-first search)

树的表示

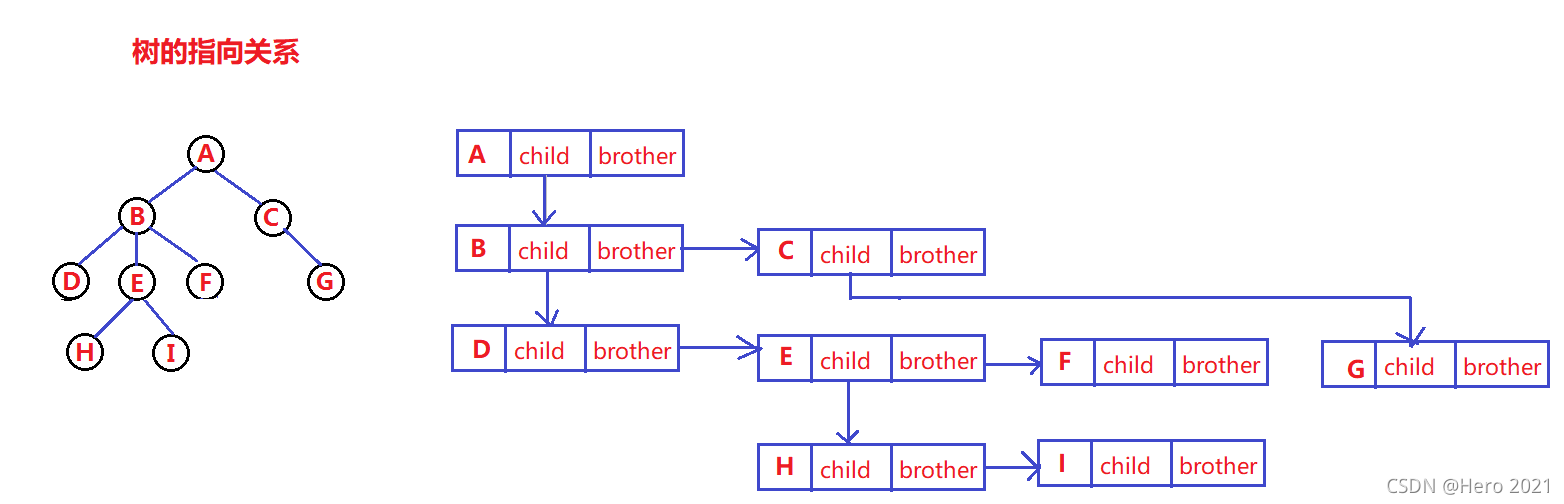
树结构相对线性表就比较复杂了，要存储表示起来就比较麻烦了，既要保存值域，也要保存结点和结点之间的关系，实际中树有很多种表示方式如：双亲表示法，孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。我们这里就简单的了解其中最常用的左孩子右兄弟法表示。

typedef int DataType;//重新定义方便以后修改要存储的数据
struct Node
{
 struct Node* firstChild1; // 第一个孩子结点
 struct Node* pNextBrother; // 指向其下一个兄弟结点
 DataType data; // 结点中的数据域
};
1
2
3
4
5
6
7

树在我们实际生活中，可以类比电脑中的文件目录，一个文件夹中包含众多的文件夹，每个文件夹又包含许多文件.