一、原理

如图1所示是灰度级为256的相位图，对于相位图中的每一个像素点，它的光强与其相应的相位是有联系的。结合式(1)可知，用于相位计算的反正切值函数的主值位于区间$(-\pi ,\pi ]$或$[0,2\pi )$之间。

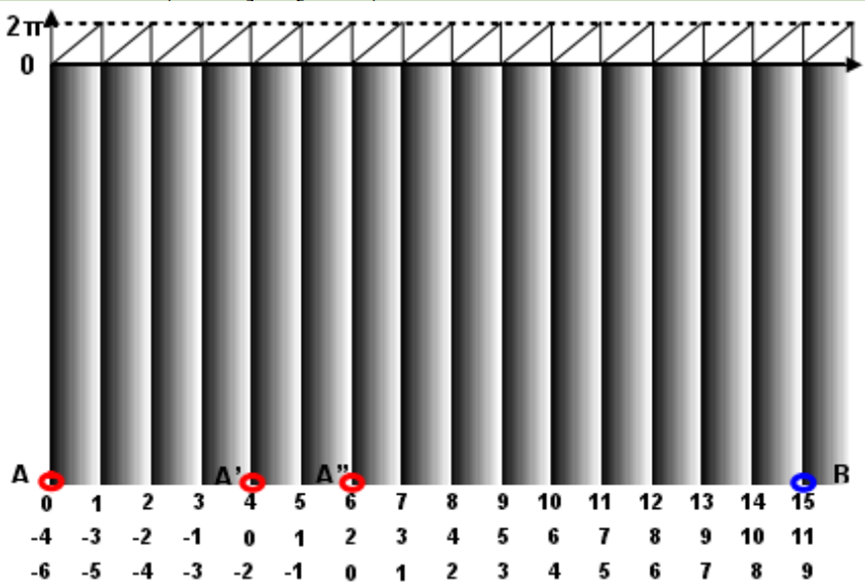
图1 相位图[1]

将折叠在$[-\pi ,\pi ]$之间的相位值还原成其真实相位值的过程称为相位展开的过程，也称为相位解包裹的过程。由采样定理可知，一个周期内至少存在两个采样点，它们相邻两像素间的真实相位差满足：

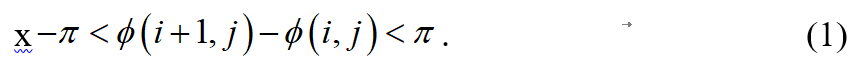
$\varphi \left(i,j\right)$为各点的相位值。相位展开的原理是：相邻两像素的相位主值进行比较，如果其相位差超出$[-\pi ,\pi ]$范围，则将后面像素对应的相位值加上或减去2π的整数倍，直到得到的相位是连续的。

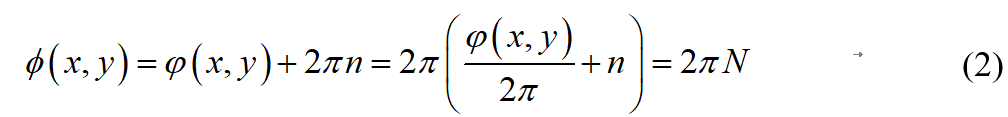
其中，$\varphi \left(x,y\right)$是解包后的相位，N是条纹数目且为实数，n是条纹级次，为N的整数部分。

相位图中的任意一点均可以被设置为0从而作为相位解包的参考点，每一点处2π的不确定性可以通过沿着从参考点到当前点的连续路线来计算2π跳跃的次数和公式(2)中的条纹级次n来解决。解包后的相位可以被认为是绝对相位。在图1中，如果选点A作为参考点，B点的绝对条纹级次是15，因为选择不同的参考点会导致其他点处的条纹级次不同，所以应该根据实际应用来选择参考点。

在理想的条件下，相位图中不存在相位不一致（如图2），因此，解包过程可以沿着相位图中的任何一条路线进行。如公式(2)所示，原始相位$\phi \left(x,y\right)$加上2π的n倍等于解包后的相位$\varphi \left(x,y\right)$，其中n为条纹级次。相位解包的关键是确定条纹级次n。通常，条纹级次可以通过公式(3)得到，利用相位图中已解包的像素来计算其相邻像素的n值。

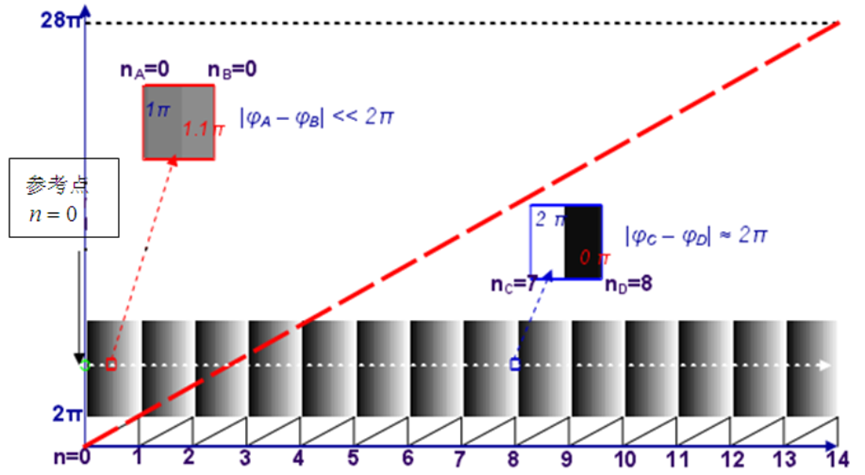
图2 一致相位的解包裹

二、实例分析

在matlab中模拟一个一维信号，如图3(a)所示。并进一步求得其包裹信号，如图3(b)，随后，对该包裹相位进行解包裹(解缠)处理，恢复得到的相位，如图3©所示。图3(d)中，将原始信号，与解包裹得到的信号绘制在同一图中，两者完全重合。

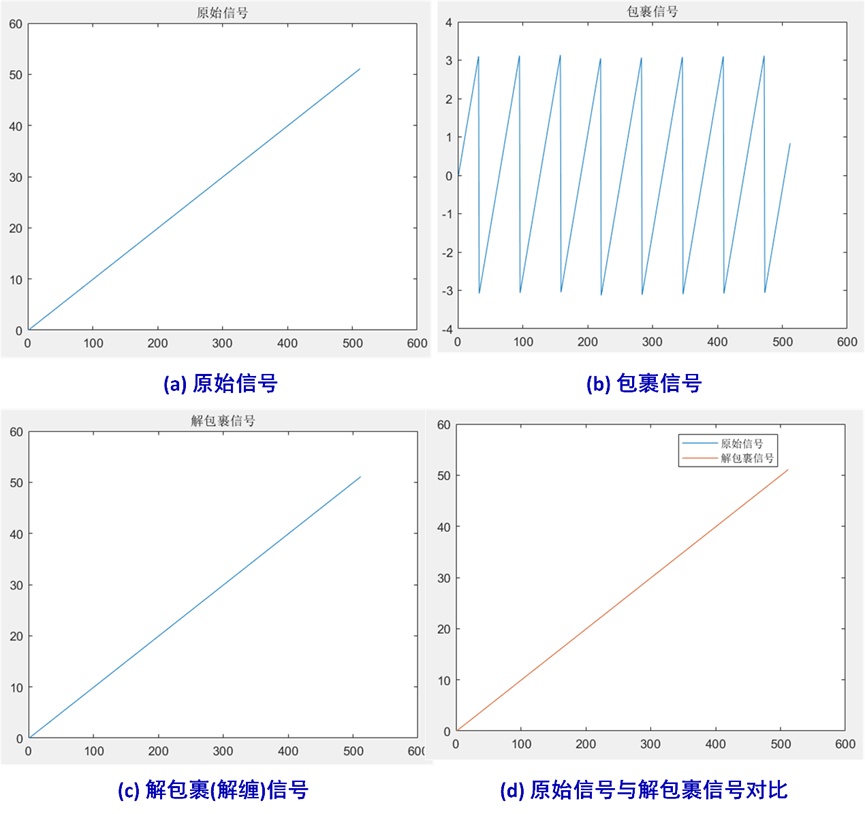
图3 相位解包裹实例

上述演示实例matlab程序可私信咨询获取：

参考文献

1. 马蛟, “基于数字光栅投影的形貌测量技术研究,” 硕士 (合肥工业大学, 2014).

---

如有问题，可私信交流讨论，博主可提供相关的技术支持。