举例解释大数定律、中心极限定理及其在机器学习中的应用

面试曾经被问到：什么是大数定律，什么是中心极限定理，大数定律在机器学习中有什么应用？大数定律在实际应用中有什么缺陷？
先说大数定律：
大数定律核心思想顾名思义，实验次数够大则随机事件发生的频率将收敛于概率。
前置知识：需要引入随机变量这个概念(也是面试常问的)，官方定义是：表示随机试验各种结果的实值单值函数。 简单地说，随机变量是指随机事件的数量表现。 比如灯泡的寿命，两颗骰子的点数和。

弱大数定律（辛钦大数定律）：设随机变量X1,X2,…Xn,…独立同分布，且具有数学期望E(Xk)=μ (k=1,2,…)，则序列$\overline{\text{X}}$=$\frac{1}{n}$${\sum }_{k=1}^n$​​依概率收敛于μ
意思是，样本越多，样本平均值越接近期望。
例如，当我们要测量某个物理量a时，在不变的条件下重复测量n次，得到的结果为X1,X2,⋯,Xn

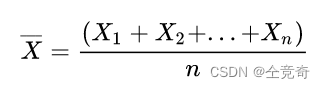
此时我们取算术平均值作为a的近似值，而且随着n的增大，
与a之间的误差会越来越小。
在数理统计中，这一定律使得用算术平均值来估计数学期望有了理论依据。
辛钦大数定律还有一个推论，更加符合直觉:
伯努利大数定律：n趋向于无穷大时，事件A在n重伯努利事件中发生的频率fn/n无限接近于事件A在一次实验中发生的概率p。
举例就是抛硬币次数越多，正面朝上的频率越来越趋近于1/2

大数定律在机器学习中的应用，最简单的就是数据集大小对模型的影响。因为如果数据集太小，样本的分布不能体现出真实世界中数据的分布，容易受到个别数据影响使得整个数据集和真实世界有很大偏差，于是学习到的模型也不能正确预测真实世界。

大数定律应用中的缺点，个人认为有两点：
1.错误标注的数据随着数据量的增大也在增加，因此不仅仅要提高数据量，还要提高数据的质量。
2.真实世界的数据不可能趋近于无穷，并且数据也不一定独立同分布。比如房价预测问题，房价数据样本随着时间推移会有变换，各个时间点采集的房价并不满足同分布。

中心极限定理，核心思想是生活中的随机变量往往是多个随机变量共同影响的结果。如果共同影响的随机变量数量足够多，那么他们影响结果相加再平均所得到的随机变量服从正态分布。
比如
一开始你手里有2个骰子，每次将他们全部扔出，记录点数算术平均，实验1000次，做出频率分布直方图；
这次手里有10个骰子，每次将他们全部扔出，记录点数算术平均，实验1000次，做出频率分布直方图；
之后再用100个骰子，每次将他们全部扔出，记录点数算术平均，实验1000次，做出频率分布直方图；
再用1000个骰子，每次将他们全部扔出，记录点数算术平均，实验1000次，做出频率分布直方图；
你会发现随着骰子数量增加，频率分布直方图越来越像正态分布。