本文为软件部2022届讲课底稿，作者5月份的时候决定出国，遂卷绩点和英语去了，本文诸多疏漏请多包涵，毕竟不是专业算法选手。

目录

背包问题的背景是什么？

多重背包的问题的背景

完全背包问题的分析

朴素做法 

多重背包的二进制优化 

二进制优化代码 

---

背包问题的背景是什么？

现在有一个背包，体积是v，给定一些物品，这些物品有他们各自的体积vi，也有他们各自的价值权重wi，想要找出怎么装背包，才可以使背包里物品的总价值最大。

问题一：背包必须装满吗？

答：不是。

多重背包的问题的背景

现在手上有一个背包，给定 n 件物品，每件物品的数量有一定的限制。物品 i 的重量是 wi，其价值为 vi，背包的容量为 C。问应如 何装入背包中的物品，使得装入背包中物品的总价值最大？

问题二：多重背包和其他背包的区别？

答：多重背包中没见物品的数量有一定的限制，完全背包问题每件物品可以选取无限次，01背包问题中每件物品只可以选取一次。

完全背包问题的分析

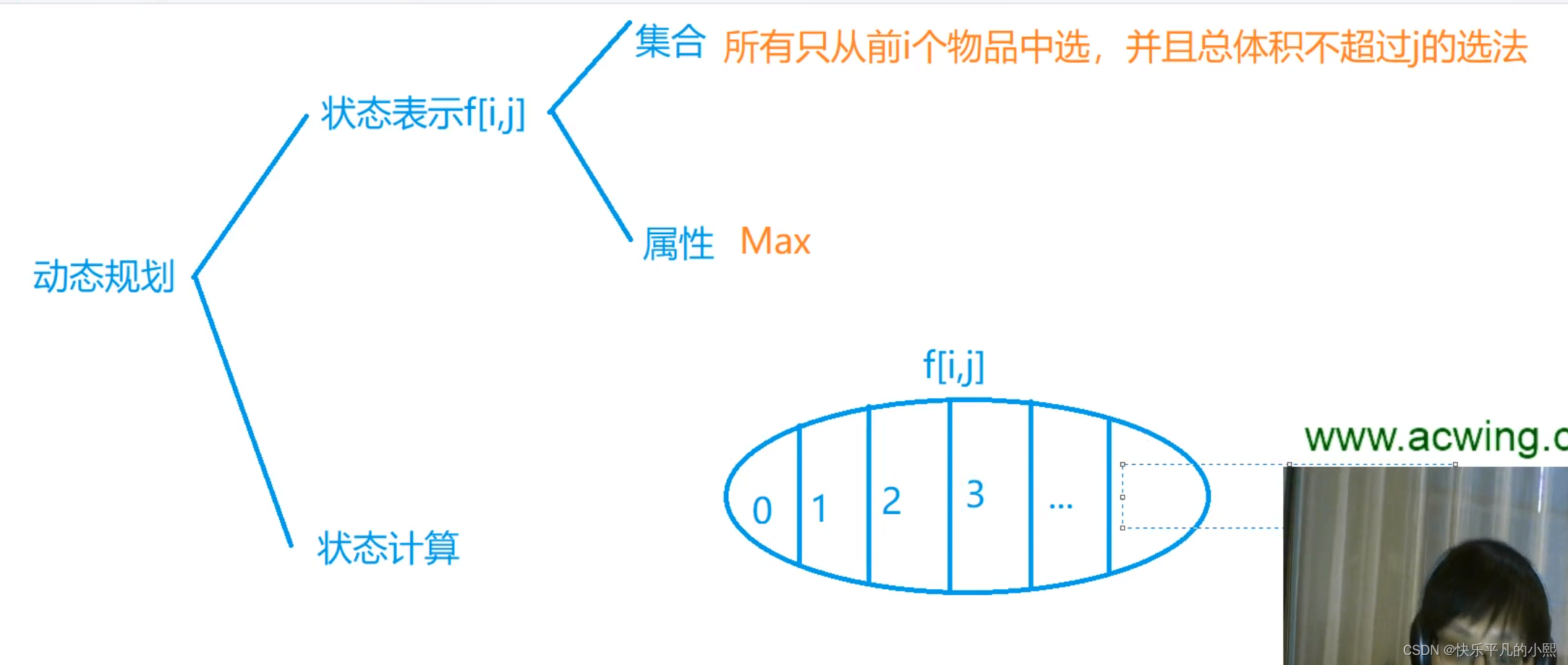问题三：多重背包问题中的公式该如何推导？ 

朴素做法 

#include
using namespace std;
int dp[105][105];
int v[105],w[105],s[105];
 
int main()
{
	int n,m;cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		cin>>v[i]>>w[i]>>s[i];
	}
	
	for(int i=1;i<=n;i++)
	{
		for(int j=0;j<=m;j++)
		{
			for(int k=0;k<=s[i]&&v[i]*k<=j;k++)//表示每种物品的件数
			{
				dp[i][j]=max(dp[i][j],dp[i-1][j-k*v[i]]+k*w[i]);
			}
		}
	}
	
	cout<
	return 0;
}

多重背包的二进制优化 

问题四：多重背包的朴素做法的时间复杂度？

答：O(n*m*k)，n表示的是物品的种类，m表示的是体积，k表示的是每种物品选取的数量上限。

问题五：多重背包的二进制优化是什么原理呢？时间复杂度又是多少呢？

答：

时间复杂度：O(n*m*log k)

原理：

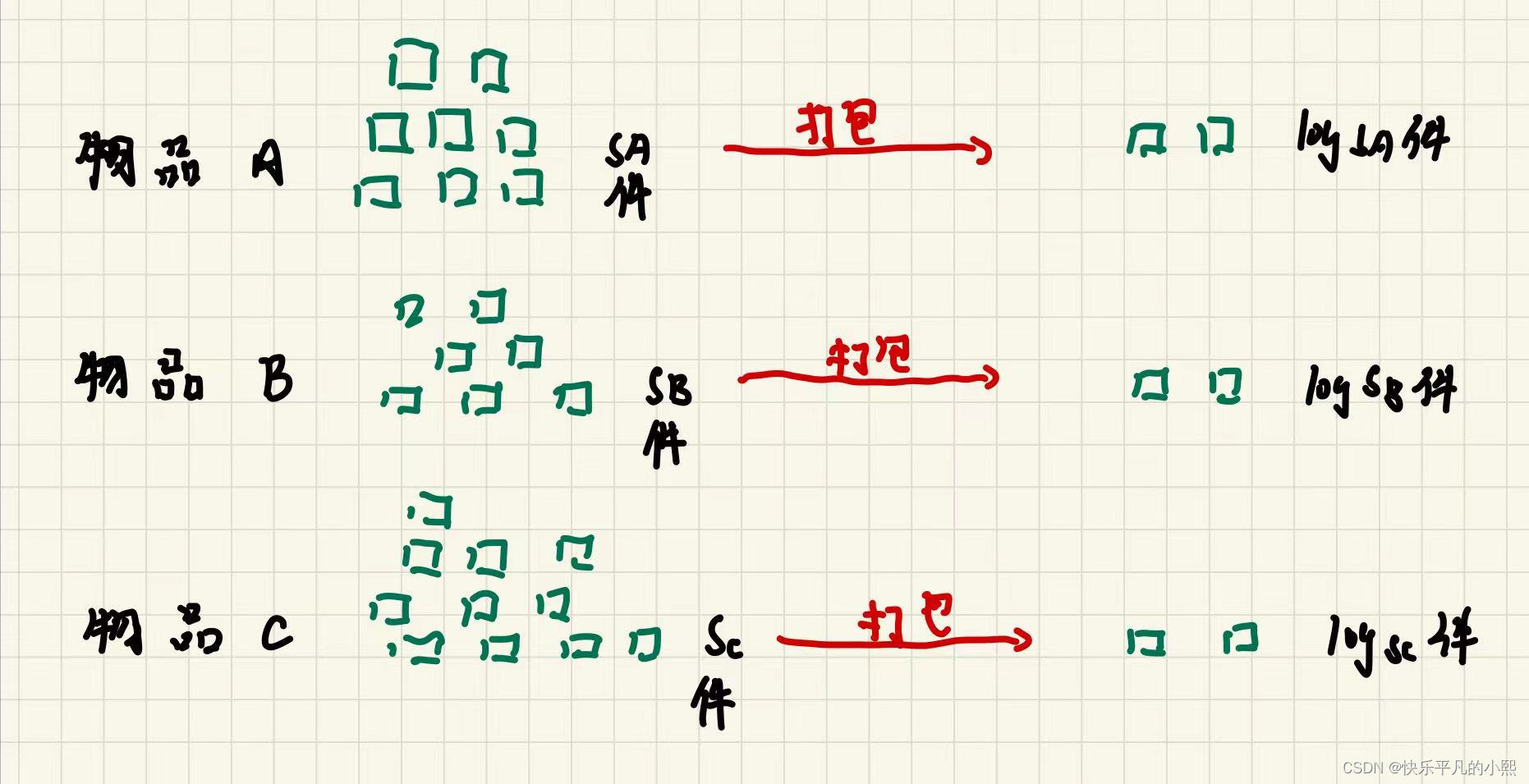
简而言之，二进制拆分，就是已知每种物件下面对应的s个物品上限，将s个物品打包拆分为log s个新的物品。这样下来已知有n种物品，每种物品的上限是s，总共就等价于打包了n*log s件物品，如下图所示。

二进制优化代码 

#include
using namespace std;
const int N=12010;const int M=2010;
int v[N],w[N],dp[M];
int n,m;
 
int main()
{
	cin>>n>>m;
	
	int cnt=1;//表示打包的第一件物品
	for(int i=1;i<=n;i++)
	{
		int a,b,s;//a表示的是体积,b表示的是价值,s表示的是第i种物品的数量
		cin>>a>>b>>s;
		int k=1;//二进制数对应的倍数
		while(k<=s)
		{
			v[cnt]=k*a;
			w[cnt]=k*b;
			k*=2;
			cnt++;
		}
		
		if(s>0)
		{
			v[cnt]=s*a;
			w[cnt]=s*b;
			cnt++;
		}
	}
	
	for(int i=1;i<=cnt;i++)
	{
		for(int j=m;j>=v[i];j--)
		{
			dp[j]=max(dp[j],dp[j-v[i]]+w[i]);
		}
	}
	
	cout<
	return 0;
}