• 二叉树算法 + 习题（JavaScript）

    二叉树（纲领篇）

    1. 是否可以通过遍历一颗二叉树得到答案？
      如果可以，用一个 traverse 函数配合外部变量来实现，这叫「遍历」的思维模式。
    2. 是否可以定义一个递归函数，通过子问题（子树）的答案推导出原问题的答案？
      如果可以，写出这个递归函数的定义，并充分利用这个函数的返回值，这叫「分解问题」的思维模式。
    3. 如果单独抽出一个二叉树节点，它需要做什么事情？需要在什么时候（前/中/后序位置）做？
      其他的节点不用你操心，递归函数会帮你在所有节点上执行相同的操作。

    二叉树遍历框架

    void traverse(TreeNode root) {
    if (root == null) {
        return;
    }
    // 前序位置
    traverse(root.left);
    // 中序位置
    traverse(root.right);
    // 后序位置
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10

    先不管所谓前中后序，单看 traverse 函数，你说它在做什么事情？

    • 它就是一个能够遍历二叉树所有节点的一个函数，和遍历数组或者链表本质没有任何区别
    /* 迭代遍历数组 */
void traverse(int[] arr) {
    for (int i = 0; i < arr.length; i++) {

    }
}

/* 递归遍历数组 */
void traverse(int[] arr, int i) {
    if (i == arr.length) {
        return;
    }
    // 前序位置
    traverse(arr, i + 1);
    // 后序位置
}

/* 迭代遍历单链表 */
void traverse(ListNode head) {
    for (ListNode p = head; p != null; p = p.next) {

    }
}

/* 递归遍历单链表 */
void traverse(ListNode head) {
    if (head == null) {
        return;
    }
    // 前序位置
    traverse(head.next);
    // 后序位置
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 单链表和数组的遍历可以是迭代的，也可以是递归的，二叉树这种结构无非就是二叉链表 - 由于没办法简单改写成迭代形式，所以一般说二叉树的遍历框架都是指递归的形式。
    • 只要是递归形式的遍历，都可以有前序位置和后序位置，分别在递归之前和递归之后。
    • 所谓前序位置，就是刚进入一个节点（元素）的时候，后序位置就是即将离开一个节点（元素）的时候，那么进一步，你把代码写在不同位置，代码执行的时机也不同。
      在这里插入图片描述
    • 比如说：让你倒序打印一条单链表，怎么搞？- 可以利用后序位置来操作
    /* 递归遍历单链表，倒序打印链表元素 */
void traverse(ListNode head) {
    if (head == null) {
        return;
    }
    traverse(head.next);
    // 后序位置
    print(head.val);
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9

    结合上面那张图，你应该知道为什么这段代码能够倒序打印单链表了吧，本质上是利用递归的堆栈帮你实现了倒序遍历的效果。

    那么说回二叉树也是一样的，只不过多了一个中序位置罢了。

    对前后序遍历的深度理解

    前中后序是遍历二叉树过程中处理每一个节点的三个特殊时间点，绝不仅仅是三个顺序不同的 List：

    • 前序位置的代码在刚刚进入一个二叉树节点的时候执行；
    • 后序位置的代码在将要离开一个二叉树节点的时候执行；
    • 中序位置的代码在一个二叉树节点左子树都遍历完，即将开始遍历右子树的时候执行。

    使用图来进行理解：
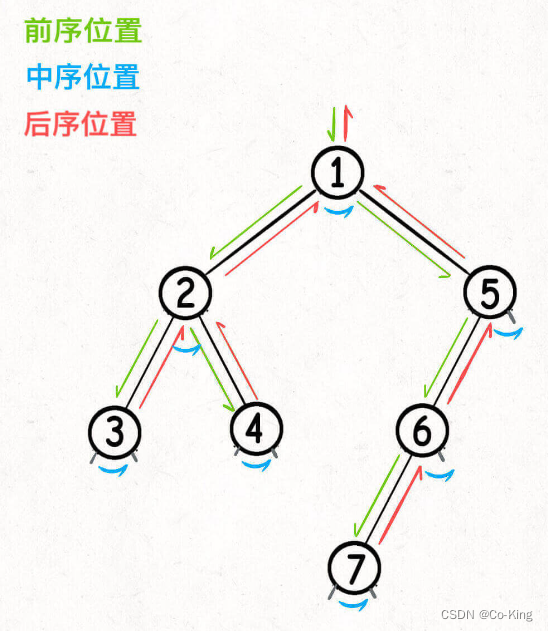
    在这里插入图片描述

    • 你可以发现每个节点都有「唯一」属于自己的前中后序位置，所以说前中后序遍历是遍历二叉树过程中处理每一个节点的三个特殊时间点。
    • 这里你也可以理解为什么多叉树没有中序位置，因为二叉树的每个节点只会进行唯一一次左子树切换右子树，而多叉树节点可能有很多子节点，会多次切换子树去遍历，所以多叉树节点没有「唯一」的中序遍历位置。

    注意：
    二叉树的所有问题，就是让你在前中后序位置注入巧妙的代码逻辑，去达到自己的目的，你只需要单独思考每一个节点应该做什么，其他的不用你管，抛给二叉树遍历框架，递归会在所有节点上做相同的操作。

    二叉树（纲领篇）

    104. 二叉树的最大深度

    题目链接

    题目描述
    在这里插入图片描述

    解决方案

    /**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
//  定义：输入一个节点，返回以该节点为根的二叉树的最大深度
var maxDepth = function(root) {
    if(root == null) return 0
    let leftMax = maxDepth(root.left)
    let rightMax = maxDepth(root.right)
    // shi
    return Math.max(leftMax, rightMax) + 1
};

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20

    144. 二叉树的前序遍历

    题目链接

    题目描述
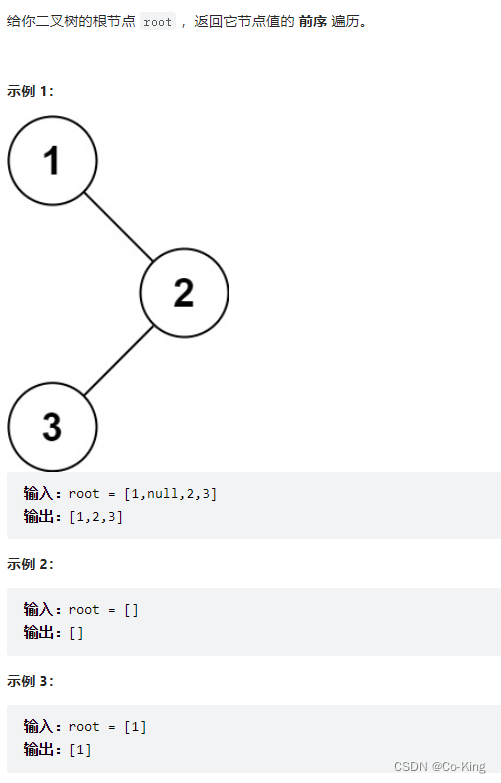
    在这里插入图片描述

    解决方案

    /**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var preorderTraversal = function(root) {
    let res = []
    var traverse = function(node) {
        if(node == null) return []
        res.push(node.val)
        traverse(node.left)
        traverse(node.right)
    }
    traverse(root)
    return res
};

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23

    543.二叉树的直径

    题目链接

    题目描述
    在这里插入图片描述
    解决方案

    所谓二叉树的直径，就是左右子树的最大深度之和，那么直接的想法是对每个节点计算左右子树的最大高度，得出每个节点的直径，从而得出最大的那个直径。

    /**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var diameterOfBinaryTree = function(root) {
    let maxDiameter = 0 // 定义一个变量 后续每次操作需要进行相应的更新
    var maxDepth = function(root) {
        if(root == null) return 0
        let leftMax = maxDepth(root.left)
        let rightMax = maxDepth(root.right)
        maxDiameter = Math.max(maxDiameter, leftMax+rightMax) // 二叉树的最大直接直径，在程序运行的过程中就进行相应更新
        return 1 + Math.max(leftMax, rightMax)
    }
    maxDepth(root)
    return maxDiameter
};

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24

    二叉树（思路篇）

    二叉树解题的思维模式

    • 是否可以通过遍历一遍二叉树得到答案？如果可以，用一个 traverse 函数配合外部变量来实现，这叫「遍历」的思维模式。
    • 是否可以定义一个递归函数，通过子问题（子树）的答案推导出原问题的答案？如果可以，写出这个递归函数的定义，并充分利用这个函数的返回值，这叫「分解问题」的思维模式。

    无论使用哪一种思维模式，你都需要思考

    • 如果单独抽出一个二叉树节点，他需要做什么，需要在什么时候（前/中/后序位置） 做？
      其他的节点不用你操心，递归函数会帮你在所有节点上执行相同的操作。

    226. 翻转二叉树（简单）

    题目链接

    题目描述
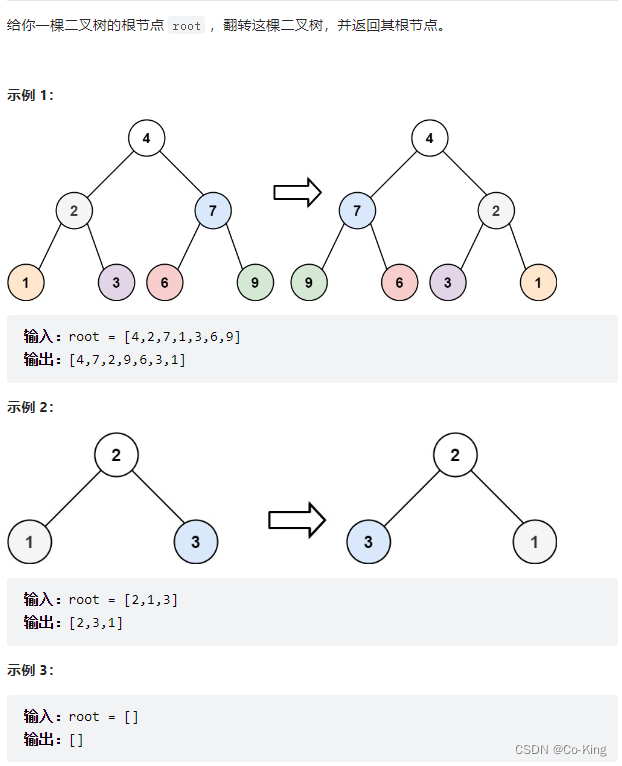
    在这里插入图片描述
    解决方案1
    1、这题能不能用「遍历」的思维模式解决？

    • 可以，我写一个 traverse 函数遍历每个节点，让每个节点的左右子节点颠倒过来就行了。
    • 单独抽出一个节点，需要让它做什么？让它把自己的左右子节点交换一下。
    • 需要在什么时候做？好像前中后序位置都可以。
    • 综上，可以写出如下解法代码：
    /**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {TreeNode}
 */
var invertTree = function(root) {
	// 遍历的思路，清楚每一个节点应该做什么，清楚每一个节点应该做些什么
    var traverse = function(root) {
        if(root == null) return null

        // 交换每个节点的左右节点
        let temp = root.left
        root.left = root.right
        root.right = temp

        // 遍历框架
        traverse(root.left)
        traverse(root.right)
    }
    traverse(root)
    return root
};

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29

    解决方案2
    2、这题能不能用「分解问题」的思维模式解决？

    • 我们尝试给 invertTree 函数赋予一个定义：
    // 定义：将以 root 为根的这棵二叉树翻转，返回翻转后的二叉树的根节点
TreeNode invertTree(TreeNode root);

    • 1
    • 2
    • 然后思考，对于某一个二叉树节点 x 执行 invertTree(x)，你能利用这个递归函数的定义做点啥？
    • 我可以用 invertTree(x.left) 先把 x 的左子树翻转，再用 invertTree(x.right) 把 x 的右子树翻转，最后把 x 的左右子树交换，这恰好完成了以 x 为根的整棵二叉树的翻转，即完成了 invertTree(x) 的定义。
    • 直接写出解法代码：
    /**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {TreeNode}
 */
var invertTree = function(root) {
    if(root == null) return null

    let left = invertTree(root.left)
    let right = invertTree(root.right)

    // 将左右子树进行调换操作
    root.left = right
    root.right = left

    return root
};

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24

    这种「分解问题」的思路，核心在于你要给递归函数一个合适的定义，然后用函数的定义来解释你的代码；如果你的逻辑成功自恰，那么说明你这个算法是正确的。

    116. 填充每个节点的下一个右侧节点指针

    题目链接

    题目描述
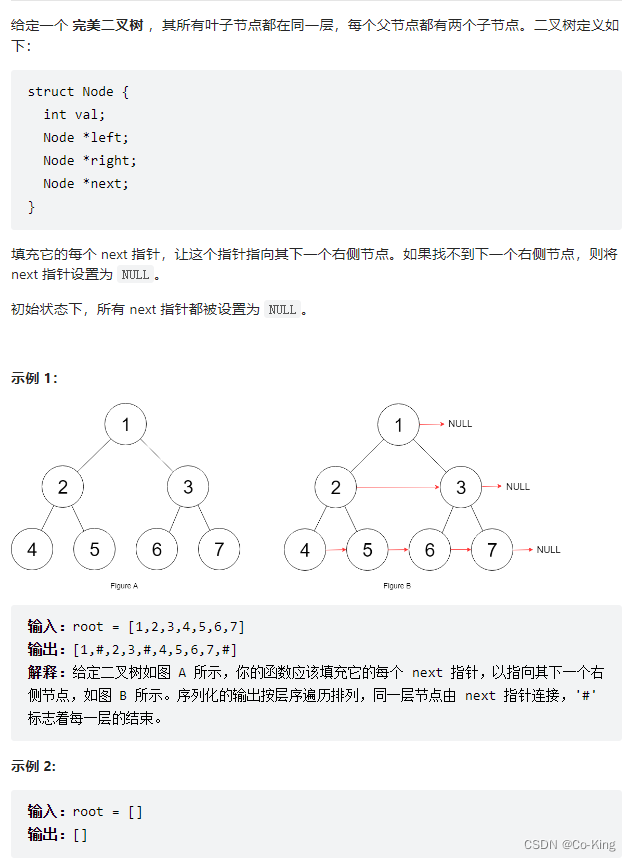
    在这里插入图片描述
    解决方案

    • 可以把二叉树的相邻节点抽象成一个【三叉树节点】，这样二叉树就变成了一颗三叉树，
    • 然后遍历这颗三叉树，把每个三叉树节点中的两个节点连接就行
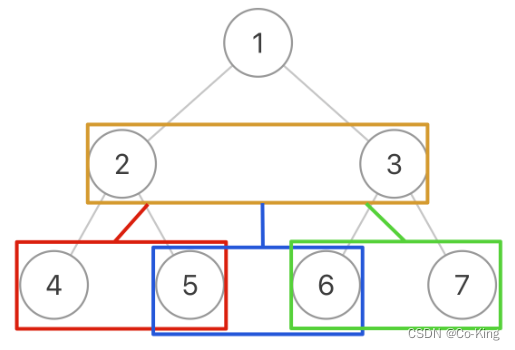
      在这里插入图片描述

    代码实现

    /**
 * // Definition for a Node.
 * function Node(val, left, right, next) {
 *    this.val = val === undefined ? null : val;
 *    this.left = left === undefined ? null : left;
 *    this.right = right === undefined ? null : right;
 *    this.next = next === undefined ? null : next;
 * };
 */

/**
 * @param {Node} root
 * @return {Node}
 */
var connect = function(root) {
    if(root == null) return null
    // 遍历三叉树
    traverse(root.left,root.right)
    return root
};
// 三叉树的遍历框架
var traverse = function(node1, node2) {
    if(node1 == null || node2 == null) {
        return 
    }
    // 前序位置，将传入的两个节点连接起来
    node1.next = node2
    // 连接相同父节点的两个子节点
    traverse(node1.left, node1.right)
    traverse(node2.left, node2.right)
    // 连接跨越父节点的两个子节点
    traverse(node1.right, node2.left)
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33

    二叉树（构造篇）

    二叉树的构造问题一般都是使用「分解问题」的思路：构造整棵树 = 根节点 + 构造左子树 + 构造右子树。

    654. 最大二叉树

    题目链接
    题目链接

    题目描述
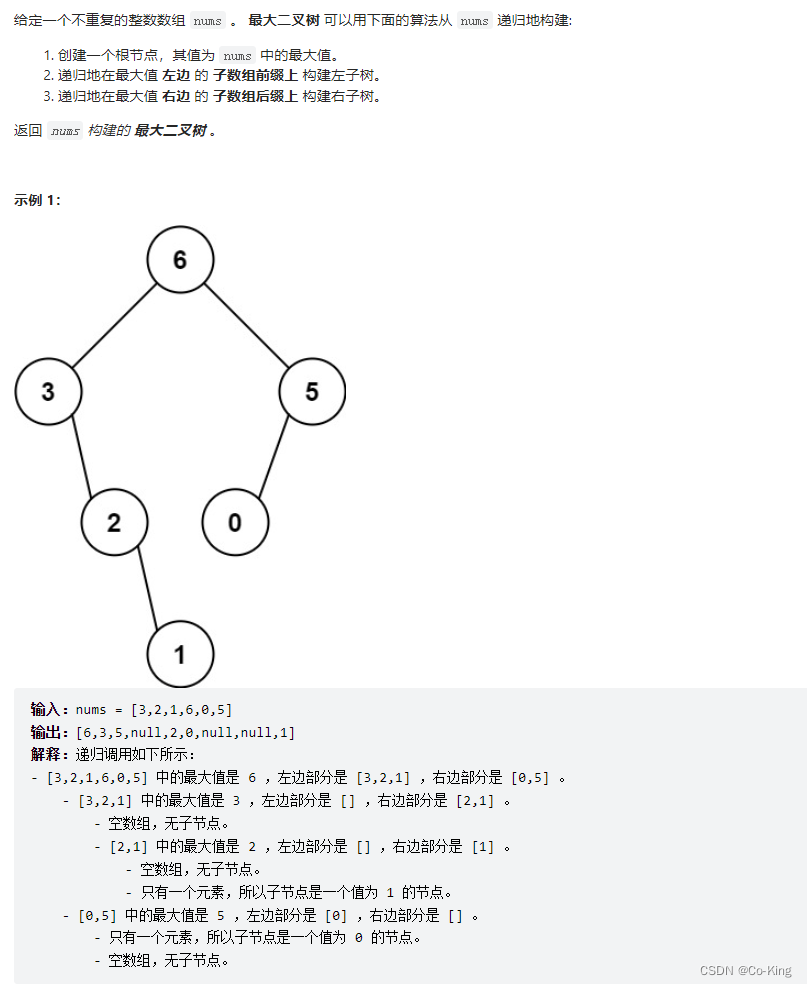
    在这里插入图片描述
    解决方案

    • 每个二叉树节点都可以认为是一棵子树的根节点，对于根节点，首先要做的当然是把想办法把自己先构造出来，然后想办法构造自己的左右子树。
    • 所以，我们要遍历数组把找到最大值 maxVal，从而把根节点 root 做出来，然后对 maxVal 左边的数组和右边的数组进行递归构建，作为 root 的左右子树。
    /**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {number[]} nums
 * @return {TreeNode}
 */
var constructMaximumBinaryTree = function(nums) {
    return build(nums, 0, nums.length-1)
};

var build = function(nums, lo, hi) {
    if(lo > hi) {
        return null // 不符合情况的话，返回null
    }
    // 找到数组中的最大值，以及其对应的索引
    let index = -1, maxVal = -100
    for(let i = lo; i <= hi; i++) {
        if(nums[i] > maxVal) {
            index = i
            maxVal = nums[i]
        }
    }
    // 先构造出根节点
    let root = new TreeNode(maxVal)
    root.left = build(nums, lo, index-1)
    root.right = build(nums, index+1, hi)

    return root
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35

    105.从前序与中序遍历序列构造二叉树

    题目链接
    题目链接

    题目描述
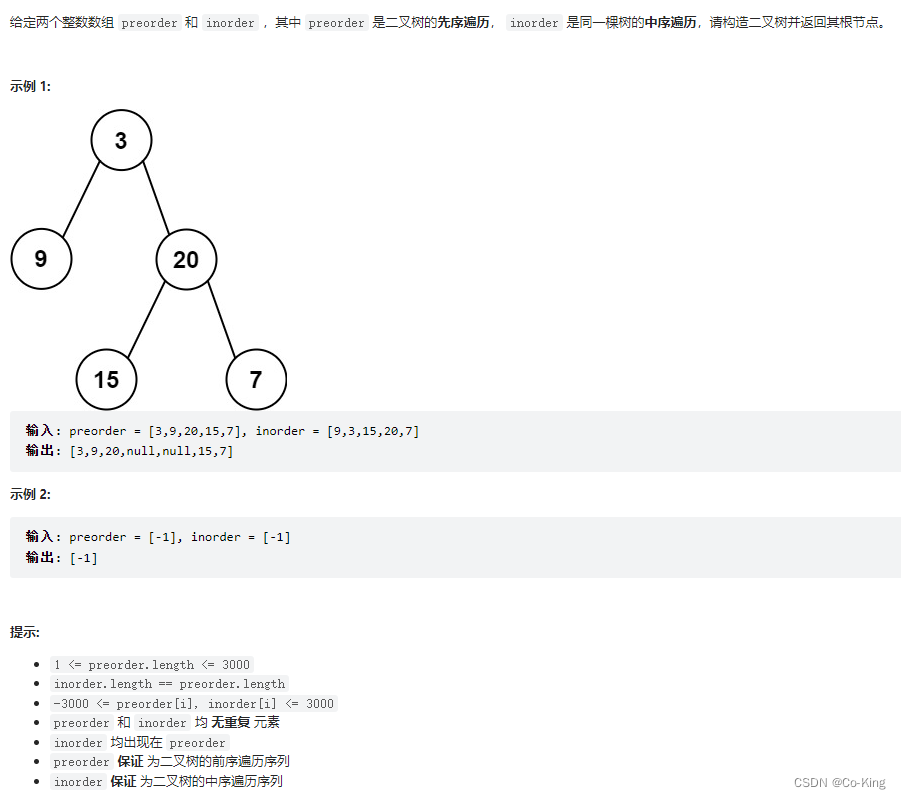
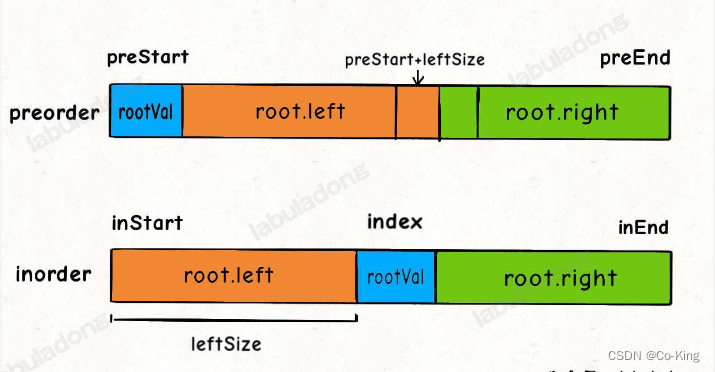
    在这里插入图片描述
    解决方案

    • 二叉树的前序和中序遍历结果的特点如下：
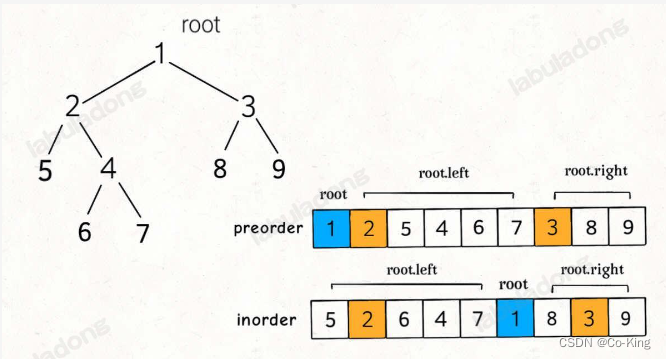
      在这里插入图片描述
    • 前序遍历结果第一个就是根节点的值，然后再根据中序遍历结果确定左右子树的节点。
      在这里插入图片描述
    /**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {number[]} preorder
 * @param {number[]} inorder
 * @return {TreeNode}
 */
var buildTree = function(preorder, inorder) {
    return buildChildrenTree(preorder, 0, preorder.length-1, inorder, 0, inorder.length-1)

};
// 构造树的时候，因为要递归调用所以要把索引都列举出来
var buildChildrenTree = function(preorder, preStart, preEnd, inorder, inStart, inEnd) {
    // 判断一个即可，因为前序和中序都是表示一个树的遍历情况
    if(preStart > preEnd) return null
    // 根节点其实就是前序遍历中的第一个节点
    let index = -1 // 找节点
    let rootVal = preorder[preStart] 
    for(let i = 0; i < inorder.length; i++) {
        if(inorder[i] == rootVal) {
            index = i 
            break
        }
    }
    // 先构造出当前根节点
    let leftSize = index - inStart
    let root = new TreeNode(rootVal)
    // 递归构造左右子树
    root.left = buildChildrenTree(preorder, preStart+1, preStart+leftSize, inorder, inStart, index-1)
    root.right = buildChildrenTree(preorder, preStart+leftSize+1, preEnd, inorder, index+1, inEnd)
    return root
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
    • 34
    • 35
    • 36
    • 37
    • 38
    • 也可以使用Map的形式来来存储inorder中的值与索引之间的映射
    var buildTree = function(preorder, inorder) {
    return buildChildrenTree(preorder, 0, preorder.length-1, inorder, 0, inorder.length-1)
};
// 构造树的时候，因为要递归调用所以要把索引都列举出来
var buildChildrenTree = function(preorder, preStart, preEnd, inorder, inStart, inEnd) {
    // 判断一个即可，因为前序和中序都是表示一个树的遍历情况
    if(preStart > preEnd) return null
    // 根节点其实就是前序遍历中的第一个节点
    // let index = -1 // 找节点
    let rootVal = preorder[preStart] 
    // 存储inorder中值到索引的映射
    let m = new Map() 
    for(let i = 0; i < inorder.length; i++) {
        // m.push([inorder[i], i])
        m[inorder[i]] = i   
    }
    console.log(m)
    let index = m[rootVal]
    // for(let i = 0; i < inorder.length; i++) {
    //     if(inorder[i] == rootVal) {
    //         index = i 
    //         break
    //     }
    // }
    // 先构造出当前根节点
    let leftSize = index - inStart
    let root = new TreeNode(rootVal)
    // 递归构造左右子树
    root.left = buildChildrenTree(preorder, preStart+1, preStart+leftSize, inorder, inStart, index-1)
    root.right = buildChildrenTree(preorder, preStart+leftSize+1, preEnd, inorder, index+1, inEnd)
    return root
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
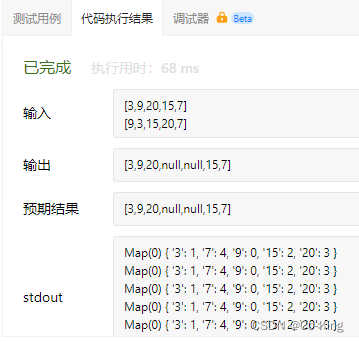
    • 此处的Map中的内容，用的是对象的键值对的形式存储的，
      在这里插入图片描述

    106.从中序与后序遍历序列构造二叉树

    题目链接

    题目描述
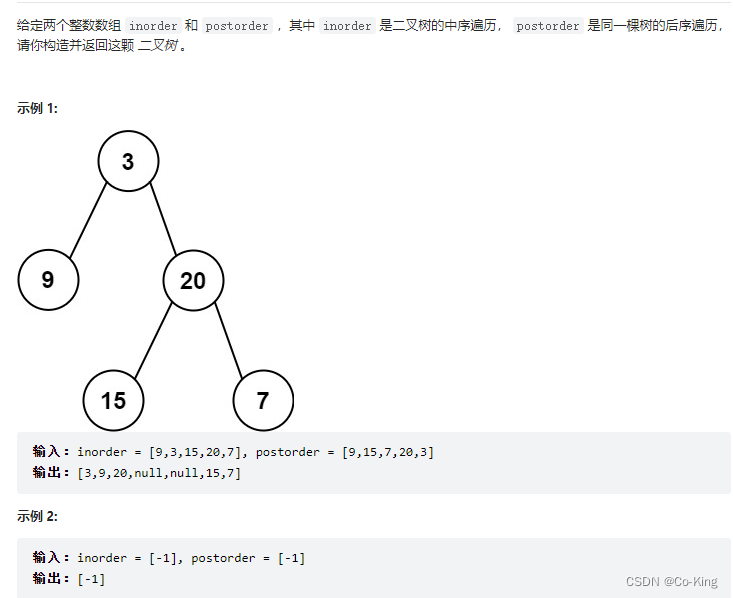
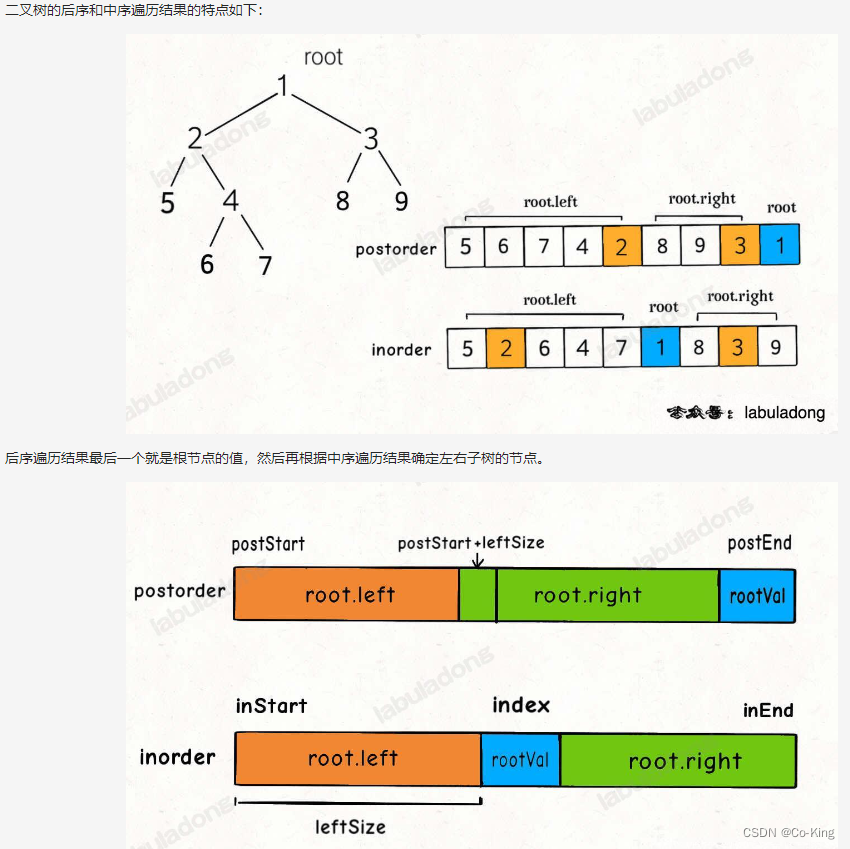
    在这里插入图片描述
    解决方案

    • 和前一题一样，都是根据二叉树的后序和中序遍历结果的特点来找到相应的下标属性的,然后根据下标来递归构建二叉树
      在这里插入图片描述
    /**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {number[]} inorder
 * @param {number[]} postorder
 * @return {TreeNode}
 */
var buildTree = function(inorder, postorder) {
    return buildPostChildren(inorder, 0, inorder.length-1, postorder, 0, postorder.length-1)
};
var buildPostChildren = function(inorder, inStart, inEnd, postorder, postStart, postEnd){
    if(inStart > inEnd) return null 
    // 根节点就是后续遍历的最后一个节点
    let index = -1
    let rootVal = postorder[postEnd] 
    for(let i = inStart; i <= inEnd; i++) {
        if(inorder[i] == rootVal) {
            index = i
        }
    }
    let leftSize = index - inStart
    // 先构造初根节点
    let root  = new TreeNode(rootVal) 
    root.left = buildPostChildren(inorder, inStart, index-1, postorder, postStart, postStart+leftSize-1)
    root.right = buildPostChildren(inorder, index+1, inEnd, postorder, postStart+leftSize, postEnd-1)
    return root
}

    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    • 8
    • 9
    • 10
    • 11
    • 12
    • 13
    • 14
    • 15
    • 16
    • 17
    • 18
    • 19
    • 20
    • 21
    • 22
    • 23
    • 24
    • 25
    • 26
    • 27
    • 28
    • 29
    • 30
    • 31
    • 32
    • 33
  • 相关阅读:
    C++模板使用
    【Python】Python 利用模块实现单例模式
    数据库三大范式
    鸿鹄工程项目管理系统em Spring Cloud+Spring Boot+前后端分离构建工程项目管理系统
    鸿翼归档：释放企业存储压力 提升数据利用效率
    网工内推 | Linux运维，六险二金，最高30K，IE认证优先
    jvm知识点总结（二）
    Prometheus Operator 实战 监控 etcd 集群
    C# 第七章『I/O数据流』◆第4节：数据流—FileStream 类
    基于Java+Spring+mybatis+vue+element实现酒店管理系统
  • 原文地址：https://blog.csdn.net/A13526_/article/details/126097602