【BP数据预测】基于matlab供需算法优化BP神经网络数据预测（含前后对比）【含Matlab源码 2032期】

一、供需算法简介

供需优化(SDO)算法是Zhao等于2019年受经济学供需机制的启发而提出的一种新型元启发式优化算法。该算法在数学上模拟了消费者的需求关系和生产者的供给关系,通过将供求机制之稳定模式和非稳定模式引入到SDO算法中,利用两种模式在给定空间中进行局部搜索和全局搜索求解待优化问题。与传统群智能算法相比,SDO算法收敛速度快、寻优精度高、调节参数少,具有较好的探索和开发能力。

将SDO算法数学描述简述如下。
a. SDO算法初始化。假设有n个市场,每个市场有d种不同的商品,每种商品都有一定的数量和价格。市场中d种商品价格表示优化问题d维变量的一组候选解,同时将市场中d种商品数量作为一组可行解进行评估,如果可行解优于候选解,则可行解替换候选解。n个市场商品价格和商品数量分别用X、Y两个矩阵表示:

式中: xi和yi 分别为第i个商品价格和数量;xij和yij分别为第j个商品在第i个市场中的价格和数量。

利用适应度函数分别对每个市场中的商品价格和数量进行评估,对于n个市场,商品价格和商品数量的适应度分别为:

b. 商品均衡数量与均衡价格。假设每种商品的均衡价格x0和均衡数量y0在每次迭代过程中都是可变的,从每个市场商品数量集合中选择一种商品数量作为其数量均衡向量,其市场适应度值越大,表示每个市场所选商品数量的概率就越大。同时,每个市场也可以根据其概率从商品价格集合中选择一种商品价格或以所有市场商品价格的平均值作为均衡价格。商品均衡数量y0表示如下:

式中:f(yi)为商品数量yi的适应度值;R(·)为比选算子(roulette wheel selection)。

商品均衡价格x0表示如下:
式中:f(xi)为商品价格xi的适应度值;r、r1为[0,1]中的随机数。

c. 供给函数和需求函数。依据均衡数量y0、均衡价格x0分别给出供给函数和需求函数:

式中:xi,t和yi,t分别为第t次迭代第i个商品价格和数量;α和β分别为需求权重和供给权重,通过调整α、β对均衡价格和均衡数量进行更新。

将式(5)插入式(6)中,可以将需求算式重写为

供应权重α和需求权重β分别为

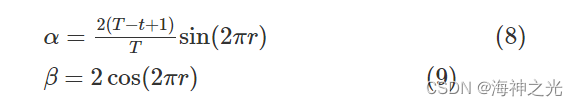
式中:T为最大迭代次数。 用变量L表示供应权重α和需求权重β的乘积,可以得到:

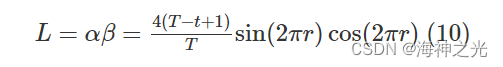
变量L有助于SDO算法在勘探和开发之间平稳过渡。|L|<1属稳定模式,通过调整供应权重α和需求权重β得到均衡价格x0周围不同的商品价格,这些商品价格可以通过随机数r在当前价格和均衡价格之间随机变化,稳定模式机制强调“开发”以改善SDO算法的局部勘探能力。|L|>1属非稳定模式,它允许任何市场中的商品价格远离均衡价格,非稳定模式机制迫使每个市场在搜索空间中加强“勘探”未知区域以提高SDO算法的全局搜索能力。

为加快SDO算法的收敛速度,进一步改善SDO局部勘探性能和全局搜索能力,将供应权重α的求解算子改进如下:

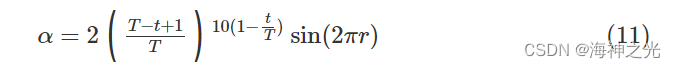
二、部分源代码

clc;
clear all;
close all
warning off
addpath pathA

%% 导入数据
% 训练集——190个样本
P_train = xlsread(‘data’,‘training set’,‘B2：G191’)’; T_train= xlsread(‘data’,‘training set’,‘H2：H191’)’;
% 测试集——44个样本
P_test=xlsread(‘data’,‘test set’,‘B2:G45’)’;T_test=xlsread(‘data’,‘test set’,‘H2:H45’)’;

N = size(P_test, 2); % 测试集样本数
M = size(P_train, 2); % 训练集样本数

%% 数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax(‘apply’, P_test, ps_input);

[t_train, ps_output] = mapminmax(T_train, 0, 1);
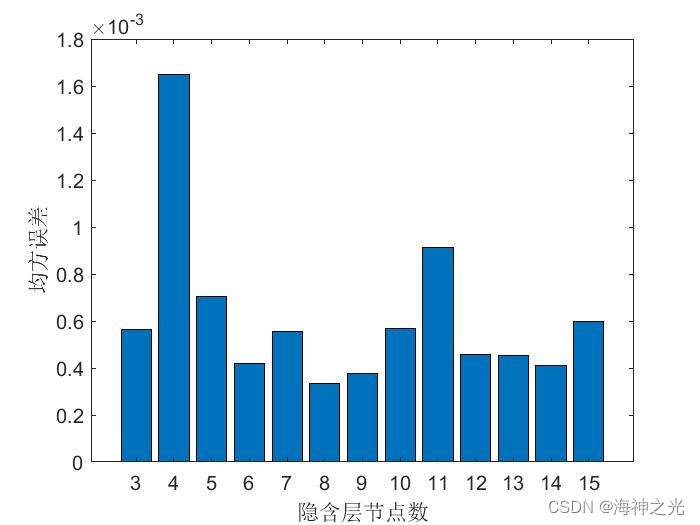
t_test = mapminmax(‘apply’, T_test, ps_output);

%% 筛选最佳隐含层节点个数
hiddenNumll=3; %隐含层下限值
m=1; %隐含层增加的步距
hiddenNumuu=15; %隐含层上限值
MSEAll=[]; %初始化mse

net0=newff(p_train,t_train,hiddenNum,{'tansig','purelin'},'trainlm');% 传递函数使用purelin，采用梯度下降法训练

%网络参数配置
net0.trainParam.epochs=1000;         % 训练次数，这里设置为1000次
net0.trainParam.lr=0.1;                   % 学习速率
net0.trainParam.goal=0.00001;                    % 训练目标最小误差
net0.trainParam.show=25;                % 显示频率，这里设置为每训练25次显示一次
net0.trainParam.mc=0.01;                 % 动量因子
net0.trainParam.min_grad=1e-6;       % 最小性能梯度
net0.trainParam.max_fail=6;               % 最高失败次数
net0.trainParam.showWindow=0;     %不显示训练界面

%训练
[net0,tr]=train(net0,p_train,t_train);%开始训练，其中inputn,outputn分别为输入输出样本

%获得训练数据归一化的仿真值
an1=sim(net0,p_train);
%计算训练集的均方误差mse
error1=an1-t_train;
[rr,ss]=size(error1);
mse1=error1*error1'/ss;
%记录每一个隐含层的mse
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

% 输出不同隐含层对应的mse值
for countt=hiddenNumllⓂ️hiddenNumuu
msee=MSEAll((countt-hiddenNumll)/m+1);
disp([‘隐含层节点数为’,num2str(countt),'时的均方误差是： ‘,num2str(msee)])
end
disp(’ ')
disp(['最佳隐含层节点数为： ',num2str(hiddenNum_best)])

figure
bar([hiddenNumllⓂ️hiddenNumuu],MSEAll)
xlabel(‘隐含层节点数’)
ylabel(‘均方误差’)
set(gca,‘fontsize’,12)

%% 初始隐层神经元个数
% 节点个数hn
inputnum=size(p_train,1);
hiddennum=hiddenNum_best;
outputnum=size(t_train,1);

%% 重新训练
w1=Best_P(1:inputnumhiddennum);
B1=Best_P(inputnumhiddennum+1:inputnumhiddennum+hiddennum);
w2=Best_P(inputnumhiddennum+hiddennum+1:inputnumhiddennum+hiddennum+hiddennumoutputnum);
B2=Best_P(inputnumhiddennum+hiddennum+hiddennumoutputnum+1:inputnumhiddennum+hiddennum+hiddennumoutputnum+outputnum);
a=net.iw{1,1};
net.iw{1,1}=reshape(w1,hiddennum,inputnum);
net.lw{2,1}=reshape(w2,outputnum,hiddennum);
net.b{1}=reshape(B1,hiddennum,1);
net.b{2}=B2;

%% BP网络训练
net.trainParam.epochs=100; %迭代次数
net.trainParam.lr=0.1;
net.trainParam.goal=0.00001; %目标精度
net.trainParam.show=100;
net.trainParam.showWindow=1; %打开训练界面

%网络训练
[net,per2]=train(net,p_train,t_train);
t_sim1=sim(net,p_train); %训练集

%% 适应度曲线
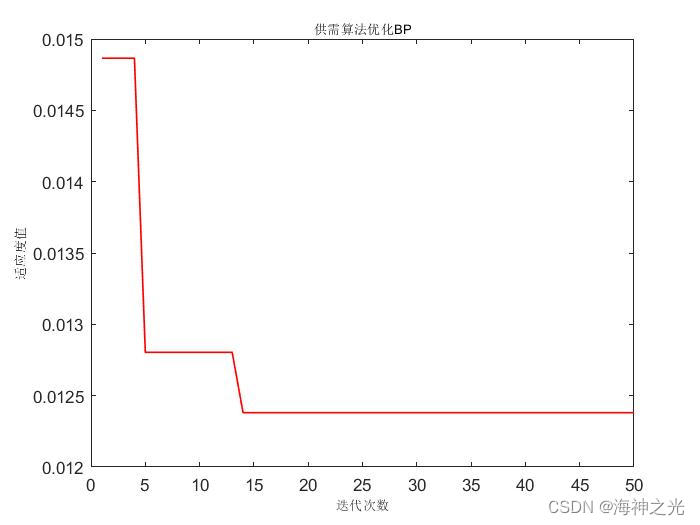
figure
plot(1 : length(BestCost), BestCost,‘r-’, ‘LineWidth’, 1);
title(‘供需算法优化BP’, ‘FontSize’, 8);
xlabel(‘迭代次数’, ‘FontSize’, 8);
ylabel(‘适应度值’, ‘FontSize’, 8);
grid off

%% 标准BP网络训练
[t_sim3,t_sim4]=BPtrain(p_train,t_train,hiddennum,p_test);

%% 数据反归一化
T_sim3 = mapminmax(‘reverse’, t_sim3, ps_output);
T_sim4 = mapminmax(‘reverse’, t_sim4, ps_output);

%% 绘图
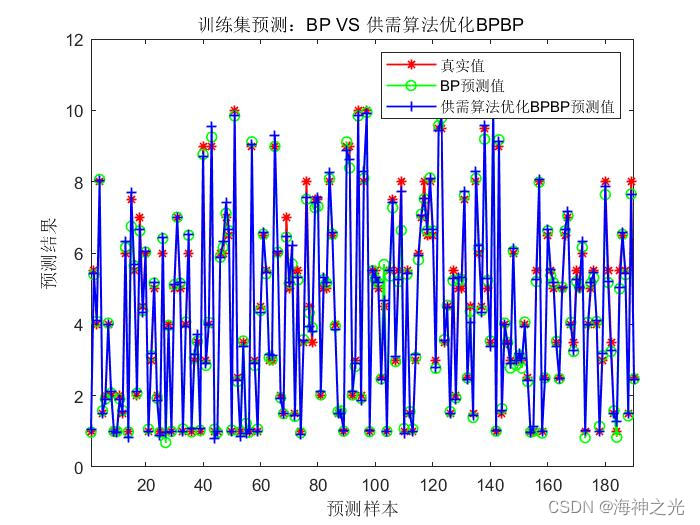
figure
plot(1: M, T_train, ‘r-*’,1: M, T_sim3, ‘g-o’, 1: M, T_sim1, ‘b-+’, ‘LineWidth’, 1)
legend(‘真实值’,‘BP预测值’,‘供需算法优化BPBP预测值’)
xlabel(‘预测样本’)
ylabel(‘预测结果’)
string = {'训练集预测：BP VS 供需算法优化BPBP '};
title(string)
xlim([1, M])
grid off

figure
plot(1: N, T_test, ‘r-*’, 1: N, T_sim4, ‘g-o’,1: N, T_sim2, ‘b-+’,‘LineWidth’, 1)
legend(‘真实值’,‘BP预测值’,‘供需算法优化BP预测值’)
xlabel(‘预测样本’)
ylabel(‘预测结果’)
string = {'测试集预测：BP VS 供需算法优化BP '};
title(string)
xlim([1, N])
grid off

%% 相关指标计算
disp([‘BP训练集数据误差：’])
[mae_BP_train,mse_BP_train,rmse_BP_train,mape_BP_train,error_BP_train,errorPercent_BP_train,R_BP_train]=calc_error(T_train,T_sim3); %
disp([‘BP测试集数据误差：’])
[mae_BP_test,mse_BP_test,rmse_BP_test,mape_BP_test,error_BP_test,errorPercent_BP_test,R_BP_test]=calc_error(T_test,T_sim4); %

disp([‘供需算法优化BP神经网络训练集数据误差：’])
[mae_train,mse_train,rmse_train,mape_train,error_train,errorPercent_train,R_train]=calc_error(T_train,T_sim1); %
disp([‘供需算法优化BP神经网络测试集数据误差：’])
[mae_test,mse_test,rmse_test,mape_test,error_test,errorPercent_test,R_test]=calc_error(T_test,T_sim2); %

三、运行结果

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]崔东文,李代华.基坑变形预测的改进供需优化算法-指数幂乘积模型[J].水利水电科技进展. 2020,40(04)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除