-
Pytorch —— 基础指北_贰 高中生都能看懂的[反向传播和梯度下降]
Pytorch ——基础指北_贰
高中生都能看懂的教程!
软件环境:
- pytorch 1.10
- pycharm
配套代码下载地址:
基础知识:
要想训练一个网络,对于梯度的理解是必不可少的,下面首先介绍梯度的一些基础概念。
0、方向余弦与向量单位化
方向余弦是一个在向量中很常见的概念,它用来标定某一个向量的方向,说起来可能会一头雾水,不过没关系,我们使用画图来理解一下。
举个例子,如下图有一个坐标系xoy,其效果如下所示:
其中包含了一个向量 l → \overrightarrow{l} l ,向量的坐标为: ( a , b ) (a,b) (a,b)
那么上文中的向量就满足如下式子:
( a a 2 + b 2 , b a 2 + b 2 ) (\frac{a}{\sqrt{a^2+b^2}},\frac{b}{\sqrt{a^2+b^2}}) (a2+b2a,a2+b2b)
上文的式子实际上就是对向量进行单位化,此时新产生的向量,实际上就是我们常说的方向向量。
方向向量实际上还可以再优化一下,我们看到图上还有两个标明的角分别是 α 和 β \alpha和\beta α和β,这两者的关系就不再多说,他们呢一对互余的角度,满足的条件就是相加等于90度。
此时我们就可以将这个式子转化成这样的形式:
a a 2 + b 2 = cos α \frac{a}{\sqrt{a^2+b^2}} = \cos{\alpha} a2+b2a=cosα
同理也有:
b a 2 + b 2 = cos β \frac{b}{\sqrt{a^2+b^2}} = \cos{\beta} a2+b2b=cosβ
这样方向的向量的表达式,就可以写为:
( a a 2 + b 2 , b a 2 + b 2 ) = ( cos α , s i n α ) (\frac{a}{\sqrt{a^2+b^2}},\frac{b}{\sqrt{a^2+b^2}}) =(\cos{\alpha},sin{\alpha}) (a2+b2a,a2+b2b)=(cosα,sinα)
实际因为角度互余上可以化为:
( c o s α , c o s β ) (cos{\alpha},cos{\beta}) (cosα,cosβ)
1、多元函数求偏导
一元函数,即有一个自变量。类似 f ( x ) f(x) f(x)
多元函数,即有多个自变量。类似 f ( x , y , z ) , 三 个 自 变 量 x , y , z f(x,y,z),三个自变量x,y,z f(x,y,z),三个自变量x,y,z
多元函数求偏导过程中:对某一个自变量求导,其他自变量当做常量即可
例1:
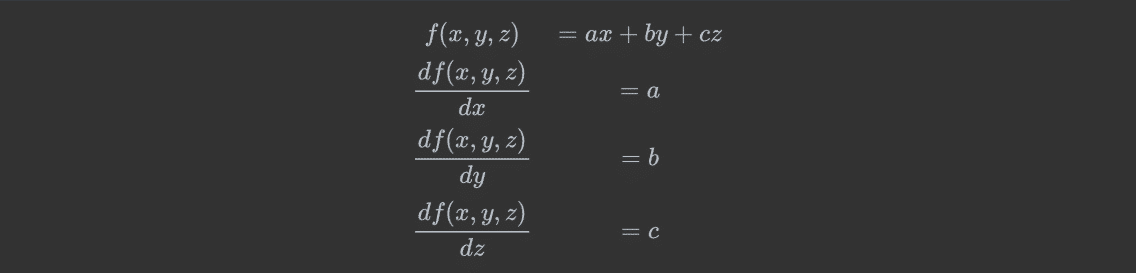
例2:
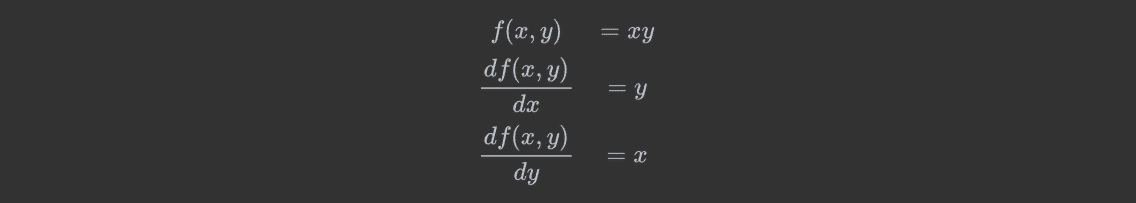
例3:

练习:
已知 J ( a , b , c ) = 3 ( a + b c ) , 令 u = a + v , v = b c J(a,b,c) = 3(a+bc),令u=a+v,v = bc J(a,b,c)=3(a+bc),令u=a+v,v=bc,求a,b,c各自的偏导数。

2、方向导数:
简单地说方向导数形容的是满足某个关系下(Y=KX+B),对于各个方向上本关系数值变化率(Y的变化率)的量化表达式。
数学推导,可参考如下文章。但是我读完以后还是没办法一下就理解,它实际上不应该是一个这么难理解的内容,我们反过来想一想,能不能从前面的基础构建出来方向导数到底是什么。
从二维、三维入手
在二维关系中Y=KX+B中我们不太好理解什么是方向导数,我们知道对于一个函数来说, y = k x + b y=kx+b y=kx+b的导数实际上是这样的:
对于函数的某一点,导数等于切线在该点的斜率,他是一个极限概念。我们不妨这样来理解这个极限的过程:
下图是某个函数,其中包含三个点如下所示:

其中A、B是函数上随机的两个点。其中A、B两点满足如下:
A = ( x 0 , f ( x 0 ) ) B = ( x 0 + Δ x , f ( x 0 + Δ ) ) A= (x_0,f(x_0))\\ B= (x_0+\Delta x,f(x_0+\Delta)) A=(x0,f(x0))B=(x0+Δx,f(x0+Δ))
然后AB两点相连接,形成一个割线,割线的斜率满足如下条件:
k A B = f ( x 0 + Δ x ) − f ( x 0 ) ( x 0 + Δ x ) − x 0 = f ( x 0 + Δ x ) − f ( x 0 ) Δ x k_{AB} = \frac{f(x_0+\Delta x) - f(x_0)}{(x_0+\Delta x) - x_0} = \frac{f(x_0+\Delta x) - f(x_0)}{\Delta x} kAB=(x0+Δx)−x0f(x0+Δx)−f(x0)=Δxf(x0+Δx)−f(x0)

当有如下情况的时候,就会产生切线和导数:
当B无限趋近于A的时候,即 Δ x \Delta x Δx无限趋近于0的时候,割线AB就会转化为切线,如下所示:
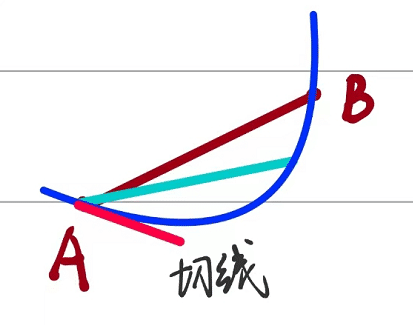
满足的数学关系如下:
KaTeX parse error: Undefined control sequence: \varliminf at position 11: k_{ab} = \̲v̲a̲r̲l̲i̲m̲i̲n̲f̲_{\Delta x \to …
而我们知道切线的斜率就是导数的值,这是在二维的情况下。三维的方向导数
在二维的情况我们已经很了解了,我们来推广到到三维的情况下来试一试,举个例子:
我们先来下一个定义:
一般情况下的三位函数的方向导数实际上是平面XOY上一点 ( x , y ) (x,y) (x,y)在三维函数的值 f ( x , y ) f(x,y) f(x,y),和其所代表的一点 ( x , y , f ( x , y ) ) (x,y,f(x,y)) (x,y,f(x,y))以向量l的方向向量为切面构成的曲线上(点(x,y))的一条切线的值。
说起来很抽象,我们举个例子就好理解一点了:
其中三维函数圆形抛物面大致如下:
Z = x 2 + y 2 Z = x^2+y^2 Z=x2+y2
如图所示: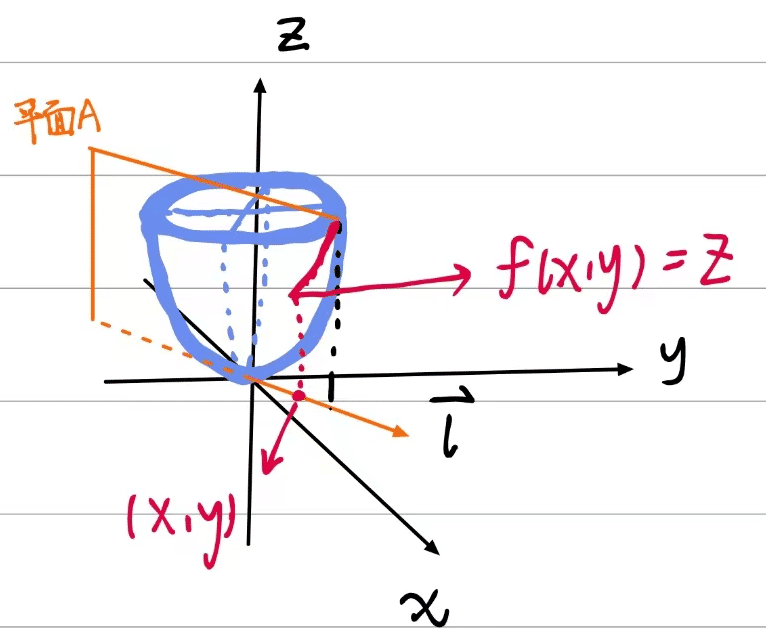
图看起来很很复杂不过没关系,我们依靠颜色来分辨一下:
红色包含两部分内容:分别是在xy平面的点 ( x , y ) (x,y) (x,y)和切面构成的曲线。
橙色包含两部分内容: l → \overrightarrow{l} l 是 X O Y XOY XOY 平面(笛卡尔坐标系)上以 P ( X 0 , Y 0 ) P(X_0,Y_0) P(X0,Y0)为始点的一条射线, e l = ( cos α , cos β ) e_l = ( \cos \alpha , \cos \beta) el=(cosα,cosβ) 是与 L 同方向的单位向量。同时还包含一个由其方向向量构建出来的平面A。
蓝色部分包含一个内容:就是函数Z。
我们来解析一下这分别什么意思
当存在一个点c从点(x,y)出发沿着方向向量变化 t t t的时候,其坐标满足如下:
C = ( x + t c o s α , y + t c o s β ) ( 其 中 角 度 和 上 文 中 的 是 一 样 意 义 ) C = (x+tcos{\alpha},y+tcos{\beta}) (其中角度和上文中的是一样意义) C=(x+tcosα,y+tcosβ)(其中角度和上文中的是一样意义)
这时候c点实际上就是黑色虚线在l上的点。这时候这个在向量上的变化轨迹就是一段向量,他的方向和l向量的方向向量是一样的,并且在函数上映射了一段曲线,如红色部分曲线所示,我们针对这一种曲线来考虑一种特殊情况,当满足这个条件的时候,曲线会如何变化?没错就是上文中二维的情况:

结果是一模一样的,只不过这里的切线是对应的在曲线上的切线,我们这里就引出方向导数的定义如下:
∂ f ∂ l ∣ ( x 0 , y 0 ) = lim t → 0 + f ( x 0 + t cos α , y 0 + t cos β ) − f ( x 0 , y 0 ) t \left. \frac{\partial f}{\partial l}\right|_{\left(x_{0}, y_{0}\right)}=\lim _{t \rightarrow 0^{+}} \frac{f\left(x_{0}+t \cos \alpha, y_{0}+t \cos \beta\right)-f\left(x_{0}, y_{0}\right)}{t} ∂l∂f∣∣∣∣(x0,y0)=t→0+limtf(x0+tcosα,y0+tcosβ)−f(x0,y0)从方向导数的定义可知,方向导数 ∂ f ∂ l ∣ ( x 0 , y 0 ) 就是函数 f ( x , y ) 在点 P 0 ( x 0 , y 0 ) 处沿方向 l 的变化率. \text { 从方向导数的定义可知,方向导数 }\left.\frac{\partial f}{\partial l}\right|_{\left(x_{0}, y_{0}\right)} \text { 就是函数 } f(x, y) \text { 在点 } P_{0}\left(x_{0}, y_{0}\right) \text { 处沿方向 } l \text { 的变化率. } 从方向导数的定义可知,方向导数 ∂l∂f∣∣∣∣(x0,y0) 就是函数 f(x,y) 在点 P0(x0,y0) 处沿方向 l 的变化率.
定理:
如果函数 f ( x , y ) 在点 P 0 ( x 0 , y 0 ) 可微分,那么函数在该点沿任一方向 的方向导数存在,且有 : \text { 如果函数 } f(x, y) \text { 在点 } P_{0}\left(x_{0}, y_{0}\right) \text { 可微分,那么函数在该点沿任一方向 的方向导数存在,且有 :} 如果函数 f(x,y) 在点 P0(x0,y0) 可微分,那么函数在该点沿任一方向 的方向导数存在,且有 :
∂ f ∂ l ∣ ( x 0 , y 0 ) = f x ( x 0 , y 0 ) cos α + f y ( x 0 , y 0 ) cos β 注 意 里 面 为 偏 导 实 际 上 就 分 解 成 了 X Y 轴 上 函 数 变 化 率 \left.\frac{\partial f}{\partial l}\right|_{\left(x_{0}, y_{0}\right)}=f_{x}\left(x_{0}, y_{0}\right) \cos \alpha+f_{y}\left(x_{0}, y_{0}\right) \cos \beta \\注意里面为偏导 实际上就分解成了X Y轴上函数变化率 ∂l∂f∣∣∣∣(x0,y0)=fx(x0,y0)cosα+fy(x0,y0)cosβ注意里面为偏导实际上就分解成了XY轴上函数变化率
其中, cos α 和 cos β \cos \alpha \text { 和 } \cos \beta cosα 和 cosβ是向量 l l l 的方向余弦。
这里再说明一下方向导数和偏导数有什么区别呢?
偏导数实际上方向导数的特例,当向量取x的正轴的时候,此时方向导数就转变为了对于x的偏导数,推导如下:
∂ f ∂ l ∣ ( x 0 , y 0 ) = lim t → 0 + f ( x 0 + t cos α , y 0 ) − f ( x 0 , y 0 ) t \left.\frac{\partial f}{\partial l}\right|_{\left(x_{0}, y_{0}\right)} = \lim _{t \rightarrow 0^{+}} \frac{f\left(x_{0}+t \cos \alpha, y_{0}\right)-f\left(x_{0}, y_{0}\right)}{t} ∂l∂f∣∣∣∣(x0,y0)=t→0+limtf(x0+tcosα,y0)−f(x0,y0)
如果你仔细看就会发现实际上这里的定义就是偏导数的定义,也就说是方向导数的一种情况。其次再说明一下,这个式子的意义在哪里:
∂ f ∂ l ∣ ( x 0 , y 0 ) = f x ( x 0 , y 0 ) cos α + f y ( x 0 , y 0 ) cos β \left.\frac{\partial f}{\partial l}\right|_{\left(x_{0}, y_{0}\right)}=f_{x}\left(x_{0}, y_{0}\right) \cos \alpha+f_{y}\left(x_{0}, y_{0}\right) \cos \beta ∂l∂f∣∣∣∣(x0,y0)=fx(x0,y0)cosα+fy(x0,y0)cosβ
实际上,我们用来计算方向导数的时候就是使用这个式子,这个式子就是将对应的方向向量分解为x轴和y轴的方向余弦来进行计算,也就说方向向量实际上是由x轴和y轴的方向余弦构成的。还有就是对于用同一个点,方向向量不同所构成的方向导数大小也不同,但是这些方向导数的方向始终会在一个平面内,这个平面就是这个点的切平面!
3、梯度:
梯度是方向导数的特例:
gradf ( x , y ) = ∂ f ∂ x i ˙ + ∂ f ∂ y j ˙ \operatorname{gradf}(x, y) = \frac{\partial f}{\partial x} \dot{i}+\frac{\partial f}{\partial y} \dot{j} gradf(x,y)=∂x∂fi˙+∂y∂fj˙
已知在某个点有方向导数存在下列关系:
∂ f ∂ l = ∂ f ∂ x cos φ + ∂ f ∂ y sin φ = { ∂ f ∂ x , ∂ f ∂ y } ⋅ { cos φ , sin φ } \frac{\partial f}{\partial l}=\frac{\partial f}{\partial x} \cos \varphi+\frac{\partial f}{\partial y} \sin \varphi=\left\{\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}\right\} \cdot\{\cos \varphi, \sin \varphi\} ∂l∂f=∂x∂fcosφ+∂y∂fsinφ={∂x∂f,∂y∂f}⋅{cosφ,sinφ}在方向 **L **上满足如下单位向量:
e → = cos φ i → + sin φ j ⃗ → \overrightarrow{\boldsymbol{e}}=\cos \varphi \overrightarrow { \boldsymbol{i}}+\sin \varphi \overrightarrow{ \vec{j} } e=cosφi+sinφj
则方向导数可转化成如下:
$$
\frac{\partial f}{\partial l}* \overrightarrow{\boldsymbol{e}}
$$
点积就相当于做一个投影,方向导数 和 梯度 之间保持一定的夹角(做点积)来构成各个方向上的方向导数。什么时候方向向量最大呢?很容易想到不存在夹角的时候就可以满足,因为此时点积最大即满足下列条件:
KaTeX parse error: No such environment: equation at position 8: \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲ \text { 只有当 }…
函数在某点的梯度是个向量,他的方向与方向导数最大值取值的方向一致,其大小正好是最大的方向导数。 梯度概念理解:如下图所示,在p点放一个热源的等温线,则热源的辐射从里到外为10°、20°、30°、40°,若一个小蚂蚁在o点,要最快逃离热源,应该往oj方向逃离,若往om方向逃离则热源的变化率为0,即一直都是20°,也就是说蚂蚁一旦确定了某个逃离方向(0°,90°)方向角逃离,只要一直沿着该方向一直走,就是最快的热源降低的方向

对于一维线性函数其导数就是梯度。
各种函数的梯度与导数的关系:
更详细的解释可以参考参考文献链接。
Tensor的梯度与反向传播
回顾机器学习
收集数据 x x x ,构建机器学习模型 f f f,得到 f ( x , w ) = Y p r e d i c t f(x,w) = Y_{predict} f(x,w)=Ypredict
如何判断模型的好坏?判断模型好坏的方法:
loss = ( Y p r e d i c t − Y true ) 2 (回归损失) loss = Y true ⋅ log ( Y predict ) (分类损失)loss=(Ypredict−Ytrue )2loss=Ytrue ⋅log(Ypredict ) (回归损失) (分类损失)
通过最终 l o s s loss loss 的输出,来反向传播计算梯度大小进而调整参数的大小实现最优解。当 l o s s loss loss 满足如图时候

计算出来梯度以后:朝着梯度变化的方向运算,随机选择一个起始点 w 0 w_0 w0,通过调整 w 0 w_0 w0,让 l o s s loss loss 函数取到最小值。
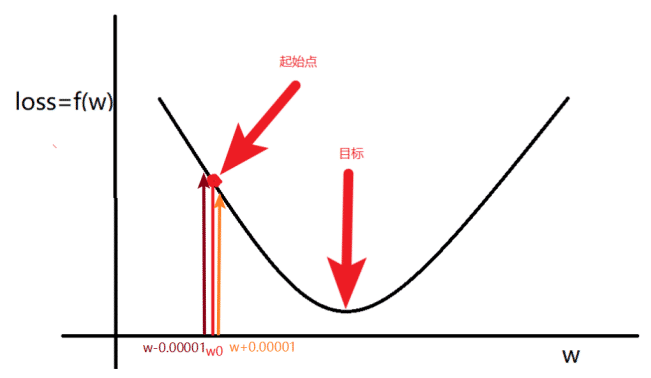
w w w的更新方法:
- 计算 w w w的梯度(导数)
$$
\begin{align*}
\nabla w = \frac{f(w+0.000001)-f(w-0.000001)}{2*0.000001}\end{align*}
$$- 更新
w
w
w
w = w − α ∇ w w = w - \alpha \nabla w w=w−α∇w
其中:
- $\nabla w <0 $ ,意味着w将增大
- $\nabla w >0 $ ,意味着w将减小
总结:梯度就是多元函数参数的变化趋势(参数学习的方向),只有一个自变量时称为导数,拥有多个时称为偏导数。
反向传播?
计算图
为了方便描述,通过图的方式来描述函数。
J ( a , b , c ) = 3 ( a + b c ) , 令 u = a + v , v = b c J(a,b,c) = 3(a+bc),令u=a+v,v = bc J(a,b,c)=3(a+bc),令u=a+v,v=bc,把它绘制成计算图可以表示为:

对每个节点求偏导可有:

反向传播的过程就是一个上图的从右往左的过程,自变量 a , b , c a,b,c a,b,c各自的偏导就是连线上的梯度的乘积:
KaTeX parse error: No such environment: align* at position 8: \begin{̲a̲l̲i̲g̲n̲*̲}̲ \frac{dJ}{da} …为什么要算反向传播?
因为要计算梯度。
实战演示:
接下来尝试计算一个简单结构的梯度,问题描述如下:
假设我们的基础模型就是
y = wx+b,其中w和b均为参数,我们使用y = 3x+0.8来构造数据x、y,所以最后通过模型应该能够得出w和b应该分别接近3和0.8。简单的来说就是拟合出满足
y = 3x+0.8这个曲线。步骤分为四步:
# 1 构造数据 # 2 设计正向传播 和 反向传播函数 来训练网络 # 3 训练 # 4 画图画出拟合出来的曲线- 1
- 2
- 3
- 4
过程如下图:
从左向右是正向传播部分
从右向左是反向传播部分

对于W和B其计算类似这里单独说B即可
对于B的梯度满足下式,值得注意的是这里的Loos求取的是平均值实际上出来的是一个标量,对于标量的梯度计算实际上也是一个平均值(这里值得思考一下)。
∂ L o s s ∂ B = ∑ i = 0 N 2 ∗ ( y i − y p i ) / N \frac{\partial Loss}{\partial B} = \sum_{i=0}^N 2*(y_i-y_{pi})/N ∂B∂Loss=i=0∑N2∗(yi−ypi)/N
反向传播后对B进行梯度下降:B = B − r a t e ∗ ∂ L o s s ∂ B B = B - rate *\frac{\partial Loss}{\partial B} B=B−rate∗∂B∂Loss
梯度下降以后再次进行正向传播即可,计算出来Y_p,最后计算出来Loss。正向传播满足下式:
Y p r e d i c t ( 0... N ) = X p r e d i c t ( 0... N ) ∗ W + B Y_{predict (0...N)} =X_{predict (0...N)}* W + B Ypredict(0...N)=Xpredict(0...N)∗W+B
代码如下:import torch import numpy as np import matplotlib.pyplot as plt # 1 构造数据 x_number = 50 x = torch.rand([x_number, 1]) y = 3 * x + 0.8 rate = 0.01 study_time = 3000 # 2 正向传播 和 反向传播 w = torch.rand([1, 1], requires_grad=True, dtype=torch.float32) b = torch.rand(1, requires_grad=True, dtype=torch.float32) y_preidct = torch.matmul(x, w) + b def forward_propagation(): global x, w, b, y_preidct y_preidct = torch.matmul(x, w) + b # 计算 loss loss = (y - y_preidct).pow(2).mean() return loss def back_propagation(): global x, w, b, loss, rate, y_preidct test = 0.0 if w.grad is not None: w.grad.data.zero_() if b.grad is not None: b.grad.data.zero_() # 反向传播 loss.backward() w.data -= w.grad * rate b.data -= b.grad * rate #此处为了验证b的梯度进行计算 # for j in range(x_number): # test += ((y[j] -y_preidct[j].item()) * 2) # print("b:", b.grad) # print("b_t:", test/x_number) # 3 训练部分 for i in range(study_time): loss = forward_propagation() back_propagation() if i % 10 == 0: print("w,b,loss", w.item(), b.item(), loss.item()) # 4 画图部分 predict = x * w + b # 使用训练后的w和b计算预测值 plt.scatter(x.data, y.data, c="r") plt.plot(x.data.numpy(), predict.data.numpy()) plt.show()- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
红色的是数据集结果蓝色是训练出来的结果:
当训练次数比较少的时候拟合曲线不正确:
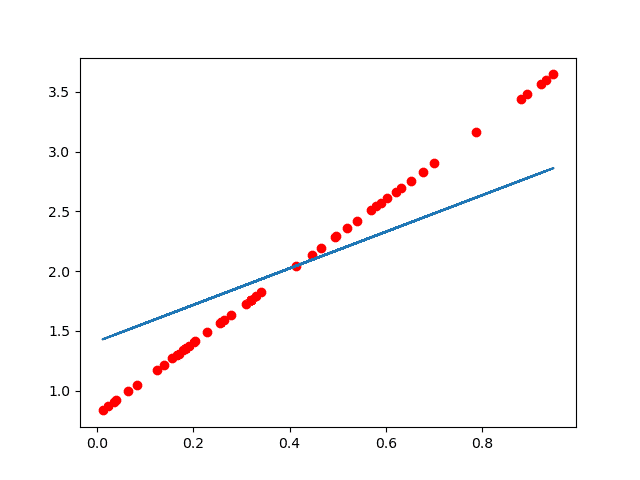
当把学习率降低(变化范围减小),增加学习次数就可以得到很好的结果:

参考文献:
-
相关阅读:
什么是 Web 3.0 及其重要性
【电力系统】基于YALMIP 的微网(光伏+风电+蓄电池+微电网+柴油机)优化调度模型附matlab代码
静态应用程序安全测试(SAST)的autofix的挑战
如何使用java雪花算法在分布式环境中生成唯一ID?
经验之谈:我为什么选择了这样一个激进的缓存大Key治理方案
【JAVA】SrpingMVC(上)—— 注解&请求与响应
Nautilus Chain 引入 $NAUT 通证,延续 $ZBC 的价值
ElementUI浅尝辄止32:NavMenu 导航菜单
git 批量clone,pull 项目
数据库事务相关知识点
- 原文地址:https://blog.csdn.net/qq_20540901/article/details/125532053
