学习笔记：机器学习之支持向量机(SVM)(上)

学习笔记：机器学习之支持向量机(SVM)(上)
活动地址：CSDN21天学习挑战赛

1 简介

        支持向量机也是一种二分类模型，它是通过在特征空间中建立间隔最大的分类器，这是有别于感知机模型的一点。

   支持向量机可分为线性可分支持向量机、线性支持向量机、非线性支持向量机。

2 函数间隔、几何间隔

2.1 函数间隔

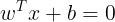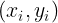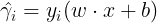
        若超平面方程为 $\large w^Tx+b=0$ ,样本点为    $\large (x_i,y_i)$ ，此时函数间隔为 $\large \hat{\gamma _i}=y_i(w\cdot x+b)$

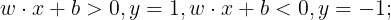
二分类问题，y取值1，-1，即 $\large w\cdot x+b> 0,y=1,w\cdot x+b<0,y=-1;$

        函数间隔表示该样本点分类的确信度，因为当y=1, 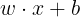$\large w\cdot x+b$ 越大,距离超平面越远，越不会分错，当y=-1是亦然。

2.2几何间隔

        几何间隔为 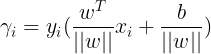   $\large \gamma _i=y_i(\frac{w^T}{||w||}x_i+\frac{b}{||w||})$ ，很类似于二维空间点到直线的距离公式的形式，不过乘了 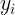$\large y_i$ , $\large y_i,w x_i+b$ 同号时分类正确。

3 线性可分支持向量机

        目的是找到一个能正确划分数据集、几何间隔最大的超平面。仅仅满足能将数据分类正确地超平面可能有很多，但是不一定最优的，因为其他数据继续划分时，这个超平面很可有失效。所以核心思想是先找到最小的几何间隔 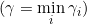$\small (\gamma =\min_i \gamma _i)$ ,并将其最大化。(我的理解是木桶效应，当短板补上了，其他地方肯定慢问题，所以最初要先找几何间隔最小的超平面)

         现在要处理的优化问题为：

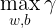
$\large \max_{w,b} \gamma$

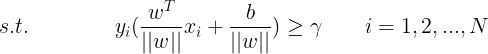
$\large s.t. \qquad \qquad y_i(\frac{w^T}{||w||}x_i+\frac{b}{||w||})\geq \gamma \qquad i=1,2,...,N$

先用函数间隔表示上边的优化问题：

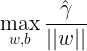
$\small \large \max_{w,b}\frac{\hat{\gamma}}{||w||}$

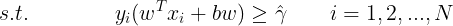
$\large s.t. \qquad \qquad y_i(w^Tx_i+bw) \geq \hat{\gamma} \qquad i=1,2,...,N$

以下有助于简化问题的求解；
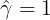
- 将 $\large \hat{\gamma }=1$
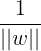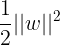- 最大化 $\large \frac{1}{||w||}$ 与最小化 $\large \frac{1}{2}||w||^2$ 是等价的。
到此就得出了线性可分支持向量机算法——最大间隔算法

线性可分支持向量机算法——最大间隔算法

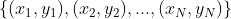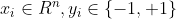输入：数据集 $\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}$ , $x_i \in R^n,y_i\in \{-1,+1\}$ ;

输出：最大间隔分离超平面、分类决策函数。

最优化问题：

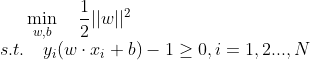
$\min_{w,b} \quad \frac{1}{2}||w||^2 \\ s.t.\quad y_i(w \cdot x_i+b)-1 \geq 0,i=1,2...,N$

求出最优解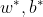,则分离超平面为 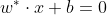$w^*\cdot x+b=0$ ,分类决策函数为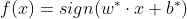 $f(x)=sign(w^* \cdot x+b^*)$

支持向量是与分离超平面最近的样本点，是使约束条件中不等式取等号的向量，支持向量决定着分类超平面，所以该模型叫做支持向量机。

参考

【十分钟机器学习系列课程】讲义（41）：SVM支持向量机-逻辑回归与支持向量机
相关阅读:
Session 和 Cookie 使用
 前端技术面试核心问题（持续更新）
RK3568开发笔记（五）：在虚拟机上使用SDK编译制作uboot、kernel和ubuntu镜像
 拿到第一个用户并提权
 互联网快讯：腾讯会议应用市场正式上线；Soul赴港递交上市申请书
 2023谷歌开发者大会直播详细脚本
 硬核 | Redis 布隆（Bloom Filter）过滤器原理与实战
 Demo27
网卡中断对cpu的不同绑定方式对Redis性能的影响
 解码字母到整数映射（Java算法每日一题）
原文地址：https://blog.csdn.net/qq_44635691/article/details/126273372

1 简介

2 函数间隔、几何间隔

2.1 函数间隔

2.2几何间隔

3 线性可分支持向量机

参考