【LeetCode】只出现一次的数字

​🌠 作者：@阿亮joy.
🎆专栏：《阿亮爱刷题》
🎇 座右铭：每个优秀的人都有一段沉默的时光，那段时光是付出了很多努力却得不到结果的日子，我们把它叫做扎根

活动地址：CSDN21天学习挑战赛

👉只出现一次的数字I👈

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。


说明：
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗？


示例 1:
输入: [2,2,1]
输出: 1


示例 2:
输入: [4,1,2,1,2]
输出: 4

思路：因为只有一个数字是出现一次的，所以我们可以利用异或的性质来解决这道题。直接一个for循环变量，将数组中的元素都进行异或操作，最后得到的结果就是只出现一次的数字。

异或的性质

• 任何数和 0 做异或运算，结果仍然是原来的数，即 n ^ 0 = n 。
• 任何数和其自身做异或运算，结果是 0，即 n ^ n = 0 。
• 异或运算满足交换律和结合律，即 a ^ b ^ a = b ^ a ^ a = b ^ (a ^ a) = b ^ 0 = b。

int singleNumber(int* nums, int numsSize)
{
	int i = 0;
	int ret = 0;
	for (i = 0; i < numsSize; i++)
	{
		ret ^= nums[i];
	}
	return ret;
}
1
2
3
4
5
6
7
8
9
10

分析：该算法的时间复杂度为 O(N)，空间复杂度为 O(1)，是这道题的最优解。

👉只出现一次的数字II👈

给你一个整数数组 nums ，除某个元素仅出现 一次 外，其余每个元素都恰出现 三次 。请你找出并返回那个只出现了一次的元素。

示例 1：

输入：nums = [2,2,3,2]
输出：3


示例 2：

输入：nums = [0,1,0,1,0,1,99]
输出：99


提示：

• 1 <= nums.length <= 3 * 10^4
• -2^31 <= nums[i] <= 2^31 - 1
• nums 中，除某个元素仅出现 一次外，其余每个元素都恰出现三次

思路：如下图所示，考虑数字的二进制形式，对于出现三次的数字，各 二进制位 出现的次数都是 33 的倍数。因此，统计所有数字的各二进制位中 11 的出现次数，并对 33 求余，结果则为只出现一次的数字。

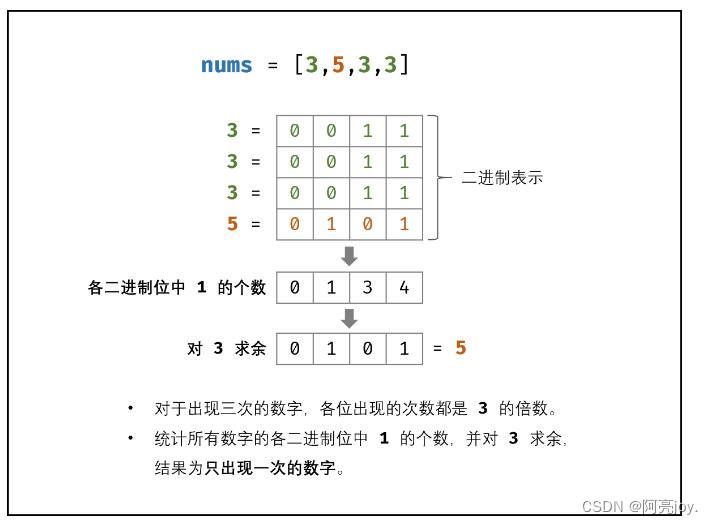
方法一

int singleNumber(int* nums, int numsSize) 
{
	int i = 0;
	int j = 0;
	int counts[32] = { 0 }; 
	//32表示32个比特位 数组counts是用于存放数组元素补码对应位上的和

	//外层循环一次，完成一个元素对应位的相加
	for (i = 0; i < numsSize; i++)
	{
		for (j = 0; j < 32; j++)
		{
			counts[j] += nums[i] & 1;//将二进制数字加到对应位上
			nums[i] >>= 1;//右移一位，将
		}
	}

	for (i = 0; i < 32; i++)
	{
		counts[i] %= 3;//模除3后，数组counts存放的就是只出现一次的数字的二进制
	}

	unsigned int ret = 0;
	for (i = 0; i < 32; i++)
	{
		ret <<= 1;//先左移是为了有对应关系：i=1，ret左移一次
		//如果ret <<= 1;语句放在后面，那么i=2，ret就左移两次了
		ret |= counts[31 - i];
		//因为左移，所以现将最高位的数字拿出来先，如果左移32次就能回到最高位上了
	}
    return ret;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

方法二

int singleNumber(int* nums, int numsSize) 
{
	int i = 0;
	int j = 0;
	int ret = 0;
	for (i = 0; i < 32; i++)//控制左移和右移的位数
	{
		int total = 0;
		for (j = 0; j < numsSize; j++)
		{
			total += ((nums[j] >> i) & 1);//补码对应位的和
		}
		if (total % 3)//如果不满足判断条件说明第i位为0，记补码最右边那位为第0位
		{
			//如果满足判断条件，就将第i位改为1
			ret |= (1u << i);//1u表示的是无符号整数1
		}
	}
	return ret;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

分析：方法一和方法二的时间复杂度和空间复杂度都分别是 O(N) 和 O(1)，但是总的来说，方法二相比于方法一更优，也更好理解。

补充知识

如果我想将一个数字的某一个二进制位上的数字改为0或1，怎么才能实现这个操作呢？接下来就为大家讲解。
代码示例：

#include 
int main()
{
	int a = 10;
	int n = 0;
	scanf("%d", &n);
	//把a的第n位置改为1
	a = a | (1 << (n - 1));
	//假设n为3
	//00000000000000000000000000001010  10的补码
	//00000000000000000000000000000100  1 << (n-1)的补码
	//按位或得
	//00000000000000000000000000001110  14的补码
	//成功将a的第三位的数字改为1
	printf("a=%d\n", a);


	//把a的第n位置改为0
	a = a & ~(1 << (n - 1));
	//因为上面将a的第三位数字改为1
	//所以a的补码为
	//00000000000000000000000000001110  14的补码
	//00000000000000000000000000000100  1 << (n-1)的补码
	//11111111111111111111111111111011  ~(1 << (n-1))的补码
	//按位与得
	//00000000000000000000000000001010 10的补码
	//成功将a的第三位的数字改为0
	printf("a=%d\n", a);

	return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

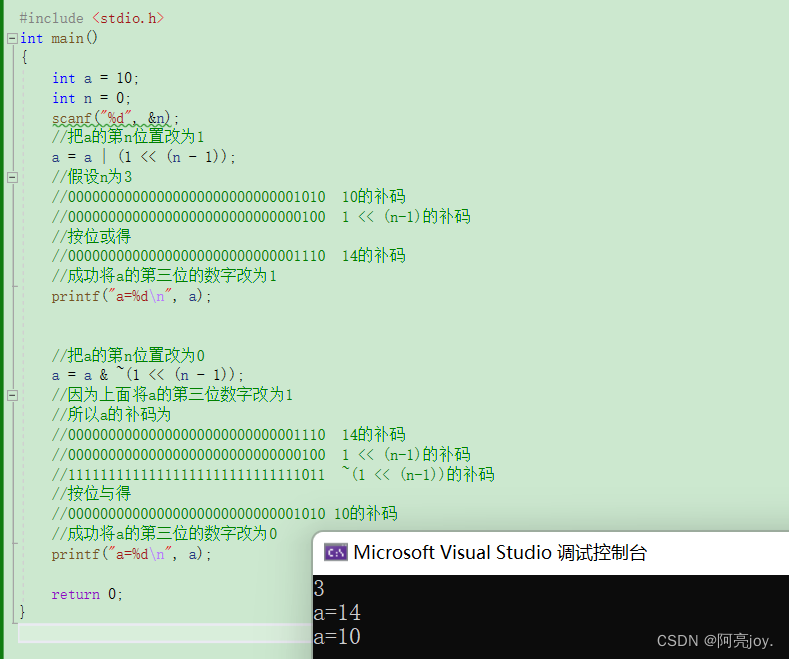
总结：

• 如果想将数字 n 的补码的第 n 位上的数字改为1，可以借助n = n | (1 << (n - 1))或者n |= 1 << (n-1)
• 如果想将数字 n 的补码的第 n 位上的数字改为0，可以借助n = n & ~(1 << (n - 1))或者` a &= ~(1 << (n - 1))

博主个人觉得这个补充知识非常的重要，如果你不知道这个小的知识点，有可能就做不出【只出现一次的数组II】这道题了。

👉只出现一次的数字III👈

给定一个整数数组 nums，其中恰好有两个元素只出现一次，其余所有元素均出现两次。 找出只出现一次的那两个元素。你可以按任意顺序返回答案。

进阶：你的算法应该具有线性时间复杂度。你能否仅使用常数空间复杂度来实现？

示例 1：

输入：nums = [1,2,1,3,2,5]

输出：[3,5]
解释：[5, 3] 也是有效的答案。

示例 2：
输入：nums = [-1,0]
输出：[-1,0]

` 提示：

• 2 <= nums.length <= 3 * 10^4
• -2^31 <= nums[i] <= 2^31 - 1
• 除两个只出现一次的整数外，nums 中的其他数字都出现两次

思路：第一步：遍历数组，把所有元素都进行异或操作得到 ret。因为数组中两个数字都只出现了一次，所以 ret 一定不为0，也就表明 ret 的补码至少有一个二进制位上的数字为1。第二步：再利用 while 循环找出 ret 的补码哪一个二进制位上的数字为1，记该位置为pos。第三步：将数组的每个元素都右移pos次，然后跟1进行按位与操作，判断结果是否为1。结果为1的为一组，结果为0的为另一种，那么两个只出现一次的数字就被分在两个组里了。再将这两组数字进行按位异或操作就能得到只出现一次的数字 num1 和 num2了。
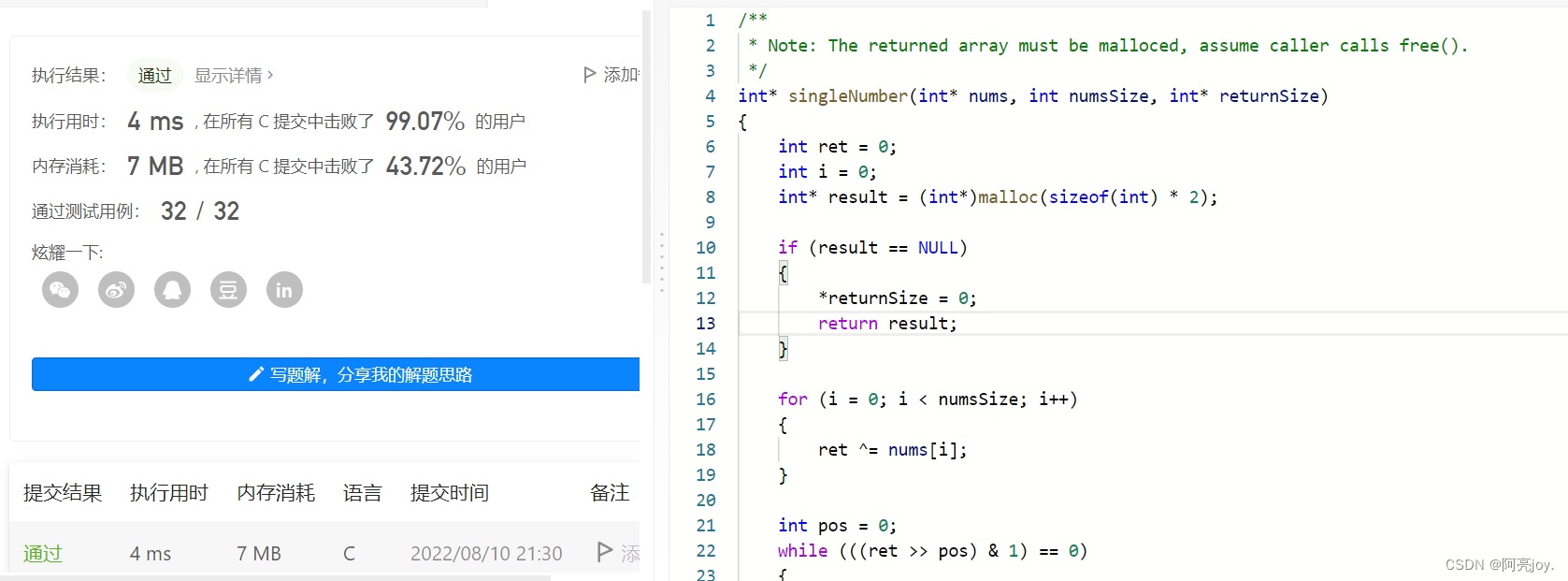
代码示例：

int* singleNumber(int* nums, int numsSize, int* returnSize) 
{
	int ret = 0;
	int i = 0;
	int* result = (int*)malloc(sizeof(int) * 2);

	if (result == NULL)
	{
		*returnSize = 0;
		return result;
	}

	for (i = 0; i < numsSize; i++)
	{
		ret ^= nums[i];
	}

	int pos = 0;
	while (((ret >> pos) & 1) == 0)
	{
		pos++;
	}

	int num1 = 0;
	int num2 = 0;
	for (i = 0; i < numsSize; i++)
	{
		if ((nums[i] >> pos) & 1)
		{
			num1 ^= nums[i];
		}
		else
			num2 ^= nums[i];
	}
	result[0] = num1;
	result[1] = num2;
	*returnSize = 2;
	return result;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

👉总结👈

LeetCode刷题网站上的【只出现一次的数字】这三道题涉及很多位运算，可以说是相当的经典。相信大家看完这篇博客都会有所收获。那就麻烦大家给个三连支持一下！谢谢大家啦！！！💖💝❣️

`