【优化求解】基于matlab遗传算法求解立体仓库出入库路径优化问题【含Matlab源码 2028期】

一、遗传算法仓库货位简介（仅供参考）

1 问题描述
1.1 自动化立体仓库出入库路径优化问题描述
自动化立体仓库如图1所示,主要是由以下几个部分组成:

1. 货架,一般为钢结构构成的存储商品的单元格,单元格内存放托盘货物;

2. 巷道堆垛机,在巷道口和货物之间穿梭,用来存取货架上面的商品;

3. 出/入库平台,临时储存物料,方便交接货位及其转载;

4. AGV或其他搬运车辆,用于联接出入库台和仓库外部输入、输出车辆的货物搬运和装卸;

5. 管理控制中心,对整个仓库的管理控制,包括整个仓库的信息、数据处理计算机、监控终端、传感器、电气控制操作台和人机界面等。
   
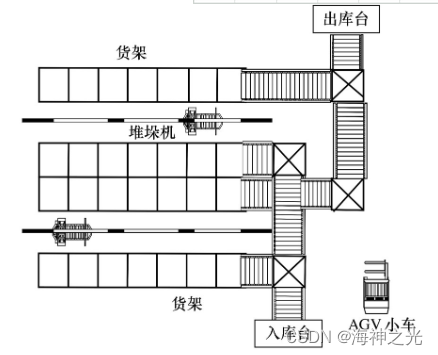
   图1 自动化立体仓库平面图

巷道堆垛机由计算机来控制,它按照计算机的指令来执行出库、入库等动作。当一批生产任务到达时,计算机将出入库的指令按照次序发送给巷道堆垛机,堆垛机按照指令顺序依次来执行出入库任务。由于出入库动作执行的顺序不一样,堆垛机的运行路径也不同,导致了执行任务所花费的时间也不一样。当生产任务较大时,合理的出入库作业路径,将极大地提高仓库的运行效率。

2 优化问题模型建立
一批生产任务中,通常包含若干个入库动作和出库动作,堆垛机出入库作业有单一作业(单一入库作业、单一出库作业)和复合作业两种;通过实践研究表明,复合作业相比单一作业更有效率[8,9],即通过将一个入库动作和出库动作配对执行来提高整体效率。如图2所示,O为堆垛机运行起始点,对M执行入库动作,对N执行出库动作,堆垛机所走的路径为O→M→N→O。

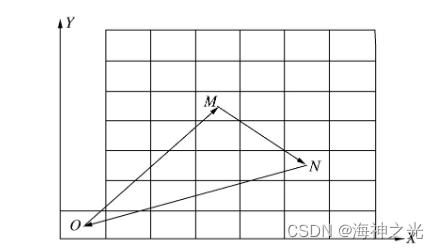
图2 堆垛机运行路径分析
为了方便计算,现假设堆垛机匀速运行,加速和制动时间忽略不计,不考虑货叉存取时间。如果货位位于i列j行,则标记为(i,j),O为(0,1)。设货架的长度和高度分别为l和h,入库作业货位位置为(a,b),出库作业货位位置为(c,d),则执行一次复合作业的时间为

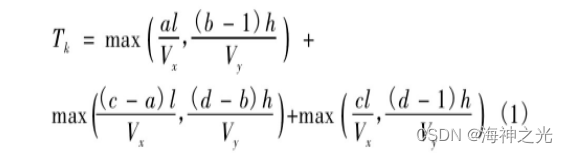
式中:Tk为一次复合作业的时间,k为第k对复合作业;Vx为水平方向的平均速度;Vy为垂直方向的平均速度。

在一批出入库作业中,出、入库作业的数目可能不一致,设有n1个入库作业,有n2个出库作业,取

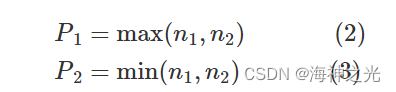
则这批出入库作业由P2个复合作业和P2-P1个单一作业组成,总作业时间为

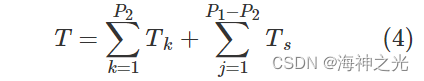
式中:Ts为单一作业的时间,设现有一个单一出库任务(e,f),则Ts表示为

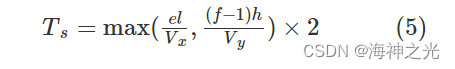
完成一批出入库作业,应该合理安排复合作业和单一作业,从而使复合作业的时间和单一作业的时间之和最小,综上所述,自动化立体仓库出入库最优路径建立如下

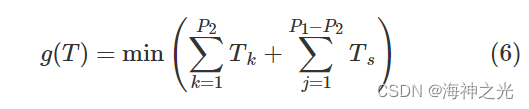
二、部分源代码

clc;close all;clear all;
%% 堆垛机路径优化

%%
vx=3;vy=1;et=1;%et为卸货/装货时间
l=1.5;h=1;%l为长，h为高
[goodin,goodout,gate]=tsp();%货物位置
n1=size(goodin,1);n2=size(goodout,1);n3=size(gate,1); %n1为入库数，n2为出库数,n3为台数
s=100;%样本数
pc=0.6;%交叉概率
pm=0.01;%变异概率
times=2000-1; %最大迭代次数
time=0; %实际迭代次数

pop=zeros(s,n1+n2+1);%初始种群+适应度
pop_fit_aver=[];%总适应度
min_dis=[];%最短时间
pop_min=[];%最短时间的基因

for i=1:s %初始化
pop(i,1:n1)=randperm(n1);
pop(i,n1+1:n1+n2)=randperm(n2);
end
clf
plot(goodin(:,1),goodin(:,2),‘ro’);%画入库点
for i=1:n1
test_t=num2str(i);
text(goodin(i,1),goodin(i,2),test_t);%标号
end
hold on,plot(goodout(:,1),goodout(:,2),‘bo’);%画出库点
for i=1:n2
test_t=num2str(i);
text(goodout(i,1),goodout(i,2),test_t);%标号
end

hold on,plot(gate(:,1),gate(:,2),‘ko’);%画门
text(gate(1,1),gate(1,2),‘a’);%标号
text(gate(2,1),gate(2,2),‘b’);%标号
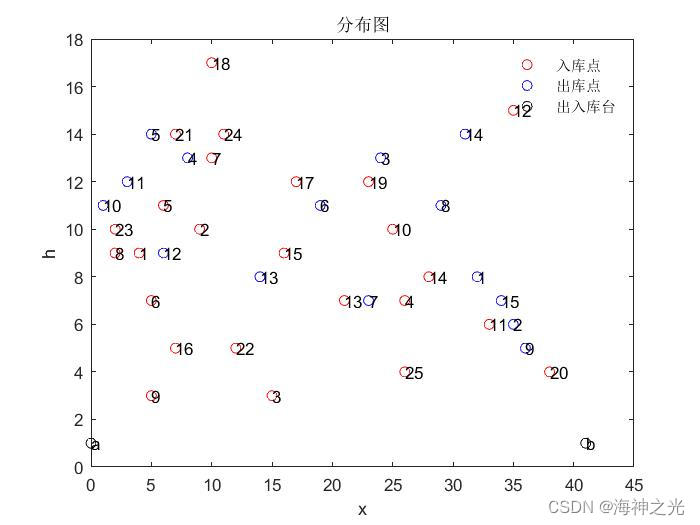
title(‘分布图’);
xlabel(‘x’);
ylabel(‘h’);
h1=legend(‘入库点’,‘出库点’,‘出入库台’) %图例说明
set(h1,‘Box’,‘off’);

[goodin_time,goodout_time]=GoodToGateTime(goodin,goodout,gate,vx,vy);%货物到两个台的时间
[individual_fit,sumfit,min1,min_index]=GroupFit(goodin_time,goodout_time,pop,s,n1,n2,n3,goodin,goodout,gate,vx,vy,et);%适应度
sumP=sumfit;
pop_fit_aver=[pop_fit_aver;sumfit/s];
min_dis=[min_dis;min1];
pop(:,n1+n2+1)=individual_fit;
fitbest=pop(min_index,:);
pop_min=[pop_min;pop(min_index,:)];
pop=ChooseParents(pop,n1,n2,s);%选择父代

for i=1:times
time=time+1;
if i<1000
[CrossOverPop]=CrossOver(s,pop,pc,n1,n2,n3,0);%采用均匀交叉
else
[CrossOverPop]=CrossOver(s,pop,pc,n1,n2,n3,1);%采用单点交叉
end
if i<500
[MutationPop]=Mutation(CrossOverPop,pm,20,n1,n2,n3);%变异
elseif i<1500
[MutationPop]=Mutation(CrossOverPop,pm,10,n1,n2,n3);%变异
else
[MutationPop]=Mutation(CrossOverPop,pm,1,n1,n2,n3);%变异
end
pop=MutationPop;%更新
[individual_fit,sumfit,min1,min_index]=GroupFit(goodin_time,goodout_time,pop,s,n1,n2,n3,goodin,goodout,gate,vx,vy,et);%适应度
sumS=sumfit;
pop_fit_aver=[pop_fit_aver;sumfit/s];
min_dis=[min_dis;min1];
pop(:,n1+n2+1)=individual_fit;
pop_min=[pop_min;pop(min_index,:)];

if i>200 && sum(pop_fit_aver(end-199:end)==pop_fit_aver(end))==200 %退出条件
    break;
end
pop=ChooseParents(pop,n1,n2,s);%选择父代
1
2
3
4

end
[a,min_index]=min(min_dis);
disp(‘最短时间’)
a
time1=1:time+1;
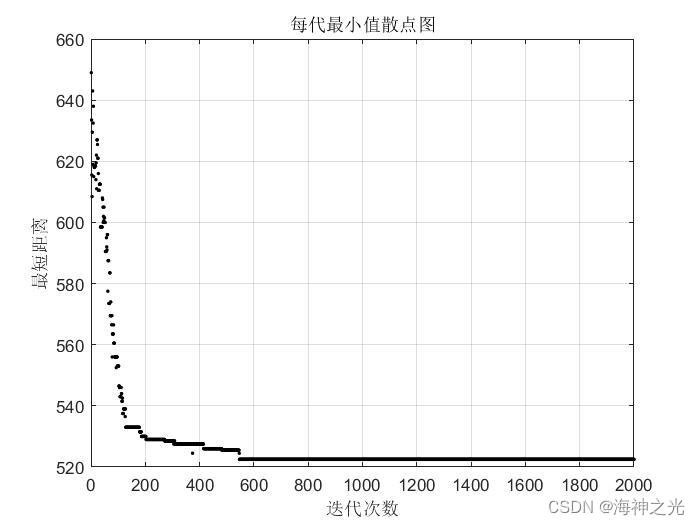
figure%画平均适应度折线图
plot(time1,min_dis,‘k.’);
grid on;
title(‘每代最小值散点图’);
xlabel(‘迭代次数’);
ylabel(‘最短距离’);
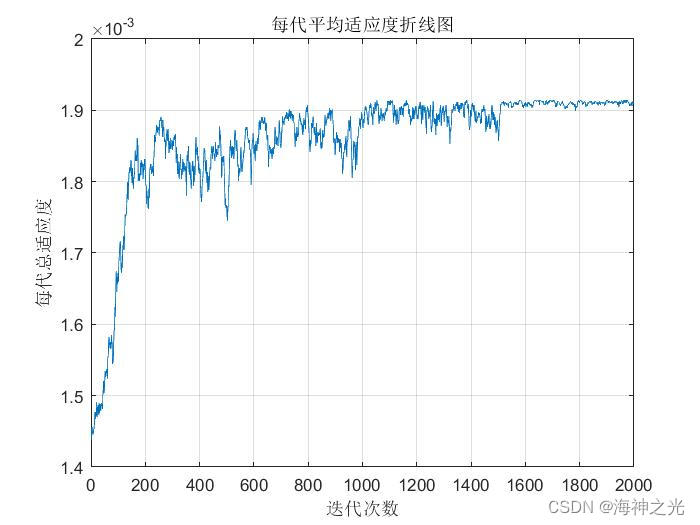
figure%画平均适应度折线图
plot(time1,pop_fit_aver);
grid on;
title(‘每代平均适应度折线图’);
xlabel(‘迭代次数’);
ylabel(‘每代总适应度’);
disp(‘最优基因’)
(pop_min(min_index,:))
DrawP(pop_min(min_index,:),goodin,goodout,goodin_time,goodout_time,gate,n1,n2,n3);

三、运行结果

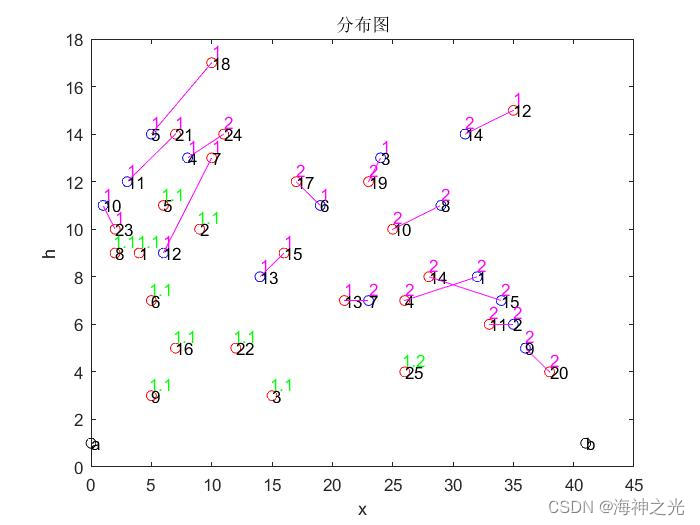
四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]朱文真,唐敦兵,王雷.基于遗传禁忌搜索算法的自动化立体仓库出入库路径优化研究[J].机械科学与技术. 2011,30(07)