机器学习算法——聚类3（k均值算法）

一、理论讲解

给定样本集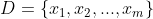，k均值（k-means）算法针对聚类所得簇划分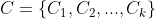最小化平方误差为：

    （1）

其中 x是簇内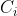的均值向量。直观来看，（1）式在一定程度上刻画了簇内样本围绕簇均值向量的紧密程度，E越小，则簇内样本相似度越高。

最小化（1）式并不容易，找到它的最优解需考察样本集D所有可能的簇划分，这是一个NP难问题。因此，k均值算法采用了贪心策略，通过迭代优化来近似求解（1）式。算法流程为：

---

输入：样本集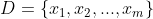;聚类簇数k

过程：从D中随机选择k个样本最为初始均值向量

repeat

        令 

        for j = 1,2,..,m do

                计算样本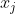与各均值向量的距离：;

                根据距离最近的均值向量确定 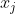的簇标记：;

                将样本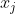划入相应的簇：

        end for

        for i=1,2,..,k do

                计算新均值向量：

                if  then

                        将当前均值向量更新为

                else

                        保持当前均值不变

                end if

        end for

until 当前均值向量均未更新

输出：簇划分

---

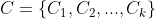
二、案例讲解

用西瓜数据集4.0解释上述算法：

 

 假定聚类簇数为3，算法开始时随机选取三个样本做为初始均值向量，即

考察样本，它与当前均值向量的距离为：

因此将划入簇中。类似地，对样本集中的所有样本考察一遍后，可得当前簇划分为

于是从分别求出新得均值向量

更新当前均值向量后，不断重复上述过程。最终在第五轮迭代产生得结果与第四轮迭代相同，于是算法终止，得到最终的簇划分。

三、代码实现

import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
import pandas as pd
 
xigua = pd.read_csv('D:/Machine_Learning/西瓜数据集4.0.csv', encoding='gbk')
data = xigua.values[:, [1,2]]
print(data.shape)
model = KMeans(n_clusters=3, random_state=10).fit(data) #默认为k-means++
label = model.predict(data)
print(label)
plt.scatter(data[:,0], data[:,1], c=label)
plt.show()

得到的结果如下：