进制转换间的那点事

前言

在学习C语言时，你是否曾被进制所支配？二进制、十进制、八进制、十六进制…明明这些数字我都认识，为什么组合在一起犹如天文数字？哈哈哈，不要怕，下面让我们一起解密进制间的那点事！

为了大家易于理解，本章就只讲解正整数之间的转化，如果想深入理解，可以去了解小数与负数之间的转换，这些大家可以适当拓展，这里就不在讲解喽。

一、常见进制数组成

🍑1.1、二进制数组成

二进制数字组成

🍑1.2、八进制数组成

八进制数字组成

🍑1.3、十进制数组成

十进制数字组成

🍑1.4、十六进制数组成

十六进制数字组成

二、进制间转换原则

在进行进制转换时有一基本原则：转换后表达的“量”的多少不能发生改变。即等大不变原则。

就像二进制中的111个苹果和十进制中的7个苹果是一样多的。

三、N进制转换为10进制

🍑3.1、按权相加法

位权： N进制整数转换为10进制整数采用 “按权相加” 法。这里的“权”指的是位权，数制中每一固定位置对应的单位值称为位权。

详解： 对于多位数，也就是当处在某一位上的“1”所表示的数值的大小，称为该位的位权。例如十进制第一位的位权为10⁰=1，第2位的位权为10¹=10，第3位的位权为10²=100；而二进制第一位位权为2⁰=1，第2位的位权为2¹=2，第3位的位权为2²=4。

位权计算规则： 由十进制、二进制整数拓展到对于 N进制整数数，整数部分第 i位的位权为 N^(i-1)

下面使用两个实例展示转换过程:👇

🍑3.2、二进制转换为10进制

📝例如：二进制数11010转化为十进制数26的过程：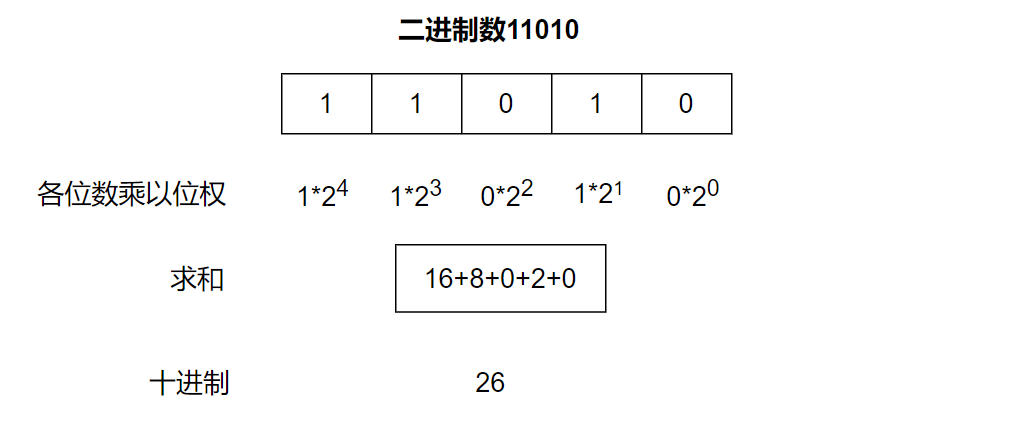

🍑3.3、十六进制转化为10进制

📝例如：十六进制数10E1转化为十进制数4321的过程：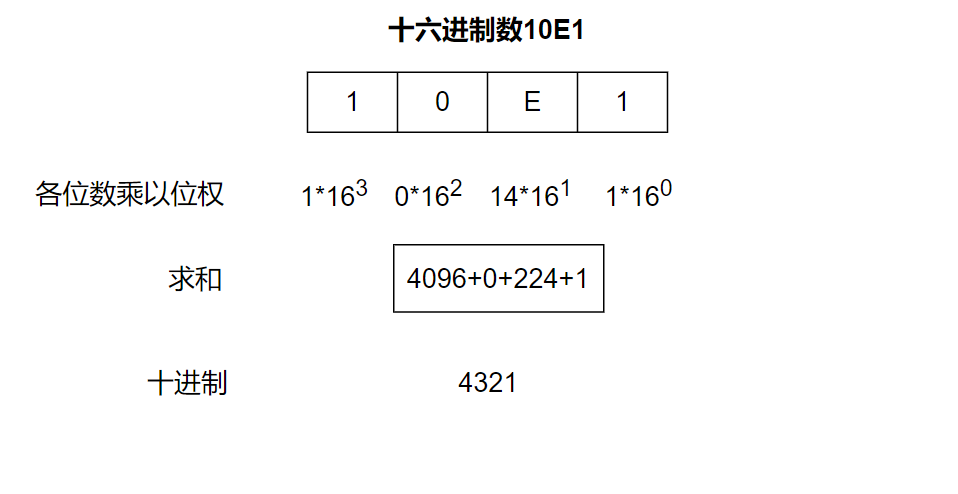

四、10进制转换为N进制

🍑4.1、“除N取余，逆序排列”法

十进制整数转换为N进制整数采用“除N取余，逆序排列”法。

具体做法是：

1. 将N作为除数，用十进制整数除以N，可以得到一个商和余数；
2. 保留余数，用商继续除以N，又得到一个新的商和余数；
3. 仍然保留余数，用商继续除以N，还会得到一个新的商和余数……；
4. 按上述步骤反复执行，直到商为零
5. 最后将先得到的余数作为低位后得到的余数作为高位，如此逆序排列就可以得到转换后的N进制数

下面用2个实例向大家展示转换过程👇

🍑4.2、十进制转换为2进制数

📝例如：十进制数42转换为2进制数101010的过程：

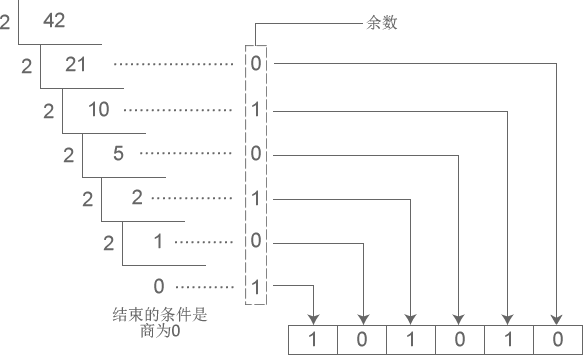
🍑4.3、 十进制数转换为8进制数

📝例如：十进制数36926转换为八进制数110076的过程：

五、二进制和八进制十六进制之间的那点事

🍑5.1、二进制与八进制之间的转换

方法： 二进制整数转换为八进制整数时，每三位二进制数字转换为一位八进制数字，运算的顺序是从低位向高位依次进行，高位不足三位用零补齐。

📝例如：二进制数1011001100转换为八进制数1314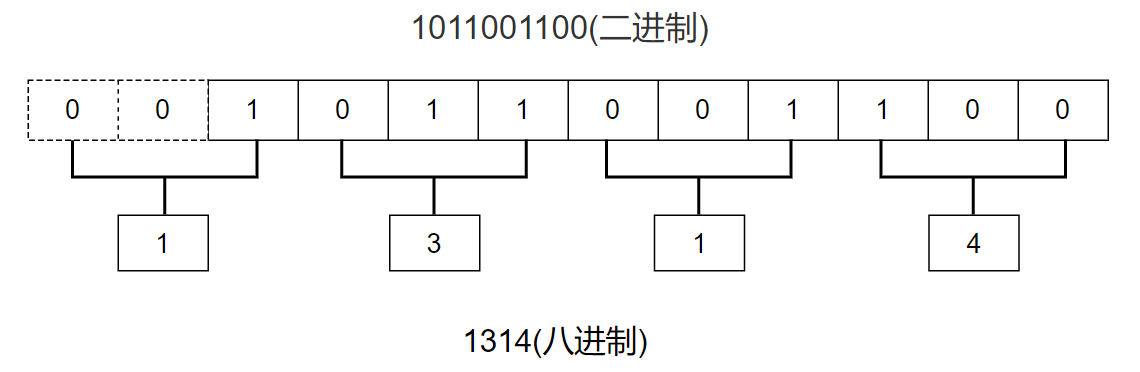

方法： 八进制整数转换为二进制整数时，思路是相反的，每一位八进制数字转换为三位二进制数字，运算的顺序也是从低位向高位依次进行。

📝例如：八进制数1024转换为二进制数1000010100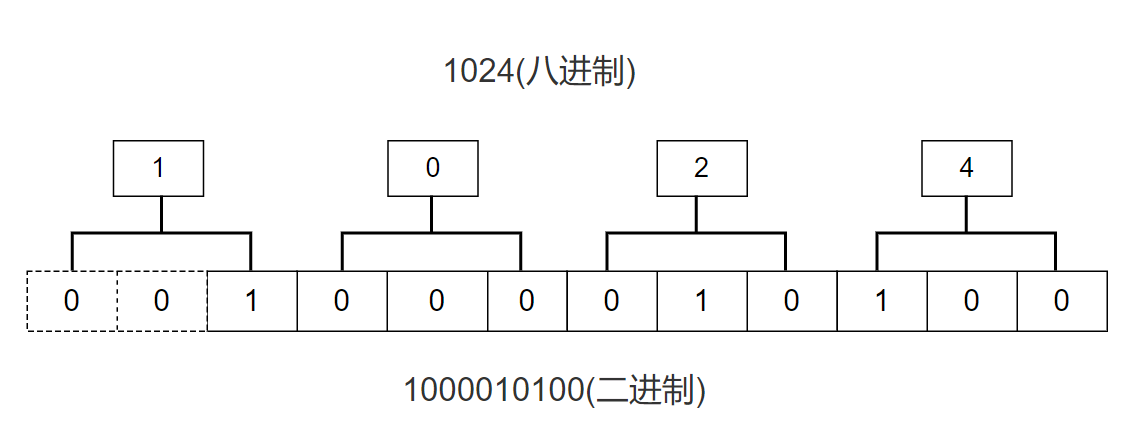

🍑5.2、二进制与十六进制之间的转换

二进制整数转换为十六进制整数时，每四位二进制数字转换为一位十六进制数字，运算的顺序是从低位向高位依次进行，高位不足四位用零补齐。

📝例如：二进制数10110101011100转换为十六进制数2D5C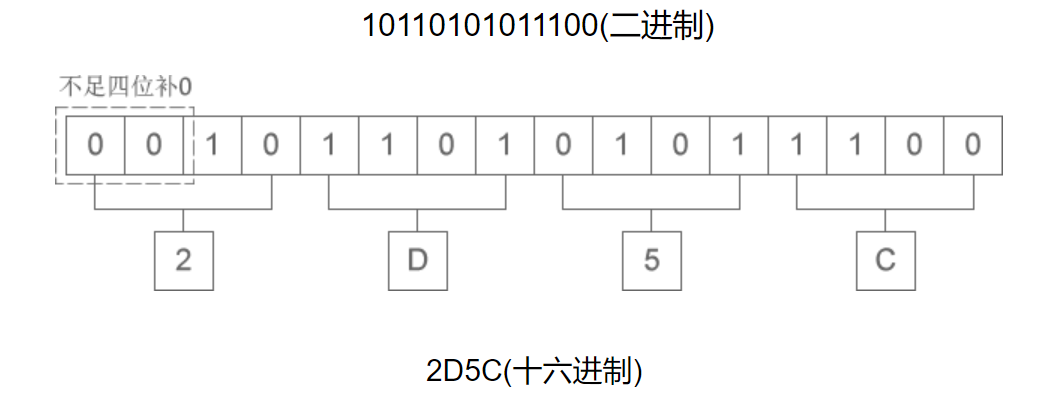

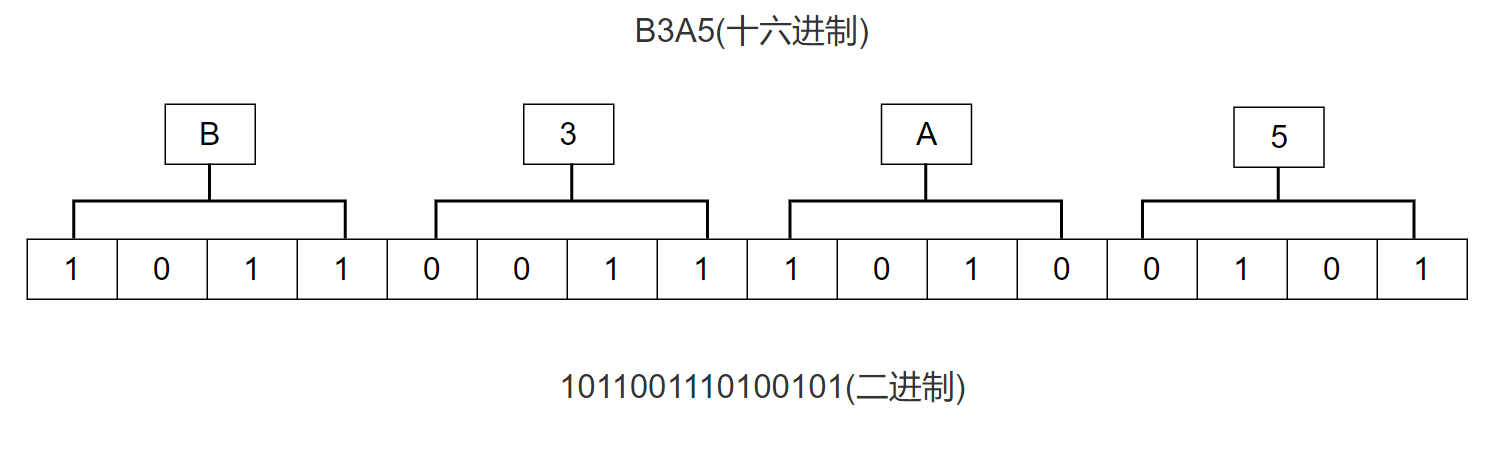
十六进制整数转换为二进制整数时，思路是相反的，每一位十六进制数字转换为四位二进制数字，运算的顺序也是从低位向高位依次进行。

📝例如：十六进制数B3A5转换为二进制数1011001110100101

六、常用进制对照表

总结

由于作者水平有限，如笔下有误，敬请留言。

如果本文对您有所帮助，请给博主点赞👍关注🙏哦，笔者会持续更新干货教程，期待与君共勉！