-
分数阶混沌系统李雅普指数和分岔图
1、内容简介
略
496-可以交流、咨询、答疑2、内容说明
%1. Chen's system:
[t, y]=FOChen([35 3 28 -7], [0.9 0.9 0.9], 100, [-9 -5 14]);
figure
plot3(y(:,1), y(:,2), y(:,3),'k');
xlabel('x(t)'); ylabel('y(t)'); zlabel('z(t)'); grid;%2. CNN - 3 cells net:
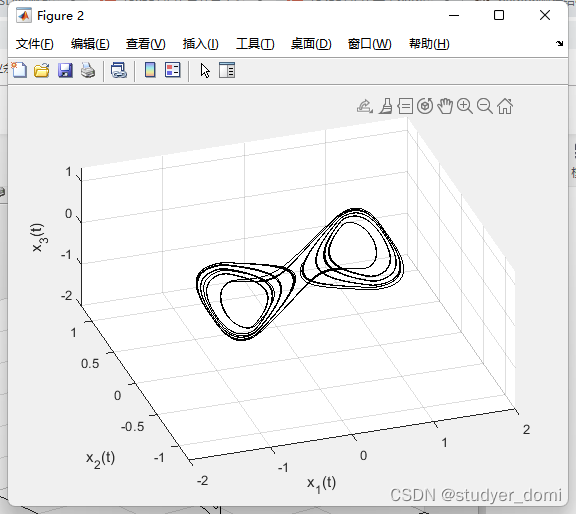
[t, y]=FO3CNN([1.24 1.1 1.0 4.4 3.21], [0.99 0.99 0.99], 100, [0.1 0.1 0.1]);
figure
plot3(y(:,1), y(:,2), y(:,3), 'k');
xlabel('x_1(t)'); ylabel('x_2(t)'); zlabel('x_3(t)'); grid;%3. Arneodo's system:
[t,y]=FOArneodo([-5.5 3.5 0.8 -1.0], [0.97 0.97 0.96], 200, [-0.2 0.5 0.2]);
figure
plot3(y(:,1), y(:,2), y(:,3), 'k');
xlabel('x(t)'); ylabel('y(t)'); zlabel('z(t)'); grid;%4. Genesio-Tesi's system:
[t, y]=FOGenTesi([1.1 1.1 0.45 1.0], [1 1 0.95], 200, [-0.1 0.5 0.2]);
figure
plot3(y(:,1), y(:,2), y(:,3),'k');
xlabel('x(t)'); ylabel('y(t)'); zlabel('z(t)'); grid;%5. Lorenz's system:
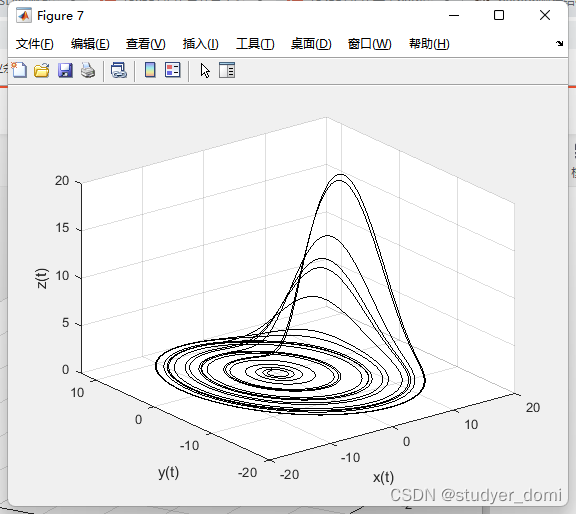
[t, y]=FOLorenz([10 28 8/3],[0.993 0.993 0.993],100,[0.1 0.1 0.1]);
figure
plot3(y(:,1), y(:,2), y(:,3), 'k');
xlabel('x(t)'); ylabel('y(t)'); zlabel('z(t)'); grid;%6. Newton-Leipnik's system:
[t, y]=FONewLeipnik([0.4 0.175], [0.95 0.95 0.95], 200, [0.19 0 -0.18]);
figure
plot3(y(:,1), y(:,2), y(:,3),'k');
xlabel('x(t)'); ylabel('y(t)'); zlabel('z(t)'); grid;%7. Rossler's system:
[t, y]=FORossler([0.5 0.2 10], [0.9 0.85 0.95], 120, [0.5 1.5 0.1]);
figure
plot3(y(:,1), y(:,2), y(:,3),'k');
xlabel('x(t)'); ylabel('y(t)'); zlabel('z(t)'); grid;%8. Lotka-Volterra system:
[t, y]=FOLotkaVolterra([1 1 1 1 2 3 2.7], [0.95 0.95 0.95], 200, [1 1.4 1]);
figure
plot3(y(:,1), y(:,2), y(:,3),'k');
xlabel('x(t)'); ylabel('y(t)'); zlabel('z(t)'); grid;%9. Duffing's system:
[t, y]=FODuffing([0.15 0.3 1], [0.9 1], 200, [0.21 0.31]);
figure
plot(y(:,1), y(:,2), 'k');
xlabel('x(t)'); ylabel('y(t)'); grid;%10. Van der Pol's oscillator:
[t, y]=FOvanDerPol(1, [1.2 0.8], 60, [0.2 -0.2]);
figure
plot(y(:,1), y(:,2), 'k');
xlabel('y_1(t)'); ylabel('y_2(t)'); grid;%11. Volta's system:
[t, y]=FOVolta([19 11 0.73],[0.99 0.99 0.99], 20, [8 2 1]);
figure
plot3(y(:,1), y(:,2), y(:,3),'k');
xlabel('x(t)'); ylabel('y(t)'); zlabel('z(t)'); grid;%12. Lu's system:
[t, y]=FOLu([36 3 20], [0.985 0.99 0.98], 60, [0.2 0.5 0.3]);
figure
plot3(y(:,1), y(:,2), y(:,3),'k');
xlabel('x(t)'); ylabel('y(t)'); zlabel('z(t)'); grid;%13. Liu's system:
[t, y]=FOLiu([1 2.5 5 1 4 4], [0.95 0.95 0.95], 100, [0.2 0 0.5]);
figure
plot3(y(:,1), y(:,2), y(:,3),'k');
xlabel('x(t)'); ylabel('y(t)'); zlabel('z(t)'); grid;%14. Chua's systems:
[t, y]=FOChuaNR([10.725 10.593 0.268 -0.7872 -1.1726], [0.93 0.99 0.92], 60, [0.6 0.1 -0.6]);
figure
plot3(y(:,1), y(:,2), y(:,3),'k');
xlabel('x(t)'); ylabel('y(t)'); zlabel('z(t)'); grid;
[t, y]=FOChuaM([10 13 0.1 1.5 0.3 0.8], [0.97 0.97 0.97 0.97], 200, [0.8 0.05 0.007 0.6]);
figure
plot3(y(:,1), y(:,2), y(:,3),'k');
xlabel('x(t)'); ylabel('y(t)'); zlabel('z(t)'); grid;
figure
plot3(y(:,4), y(:,1), y(:,2),'k');
xlabel('w(t)'); ylabel('x(t)'); zlabel('y(t)'); grid;%15. Financial system:
[t, y]=FOFinanc([1 0.1 1],[1 0.95 0.99],200, [2 -1 1]);
figure
plot3(y(:,1), y(:,2), y(:,3),'k');
xlabel('x(t)'); ylabel('y(t)'); zlabel('z(t)'); grid;
3、仿真分析


4、参考论文略
-
相关阅读:
1x1卷积的作用
Bevy的一些窗口设置
hadoop集群搭建
Spring Cloud Gateway 服务网关的部署与使用详细介绍
Nginx负载均衡之动态更新upstream
火遍国内外IT技术圈,豆瓣 9.7!这本技术书籍直接封神了
数据结构与算法(三)
合并区间问题
【学习笔记14】JavaScript的循坏语句
AutoGPT:让 AI 帮你完成任务事情 | 开源日报 No.54
- 原文地址:https://blog.csdn.net/qingfengxd1/article/details/126245476