• 图(最小生成树、最短路径、关键路径)

    6.1-1 图的基本概念

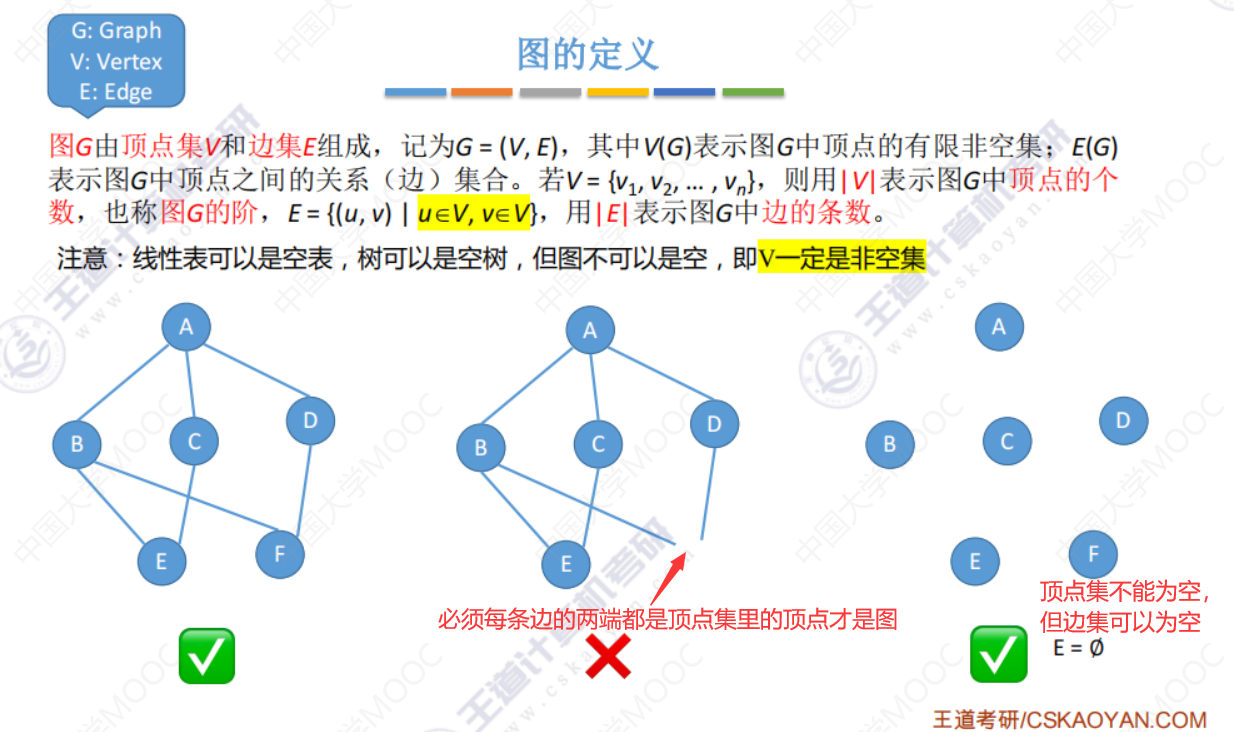
    图的定义

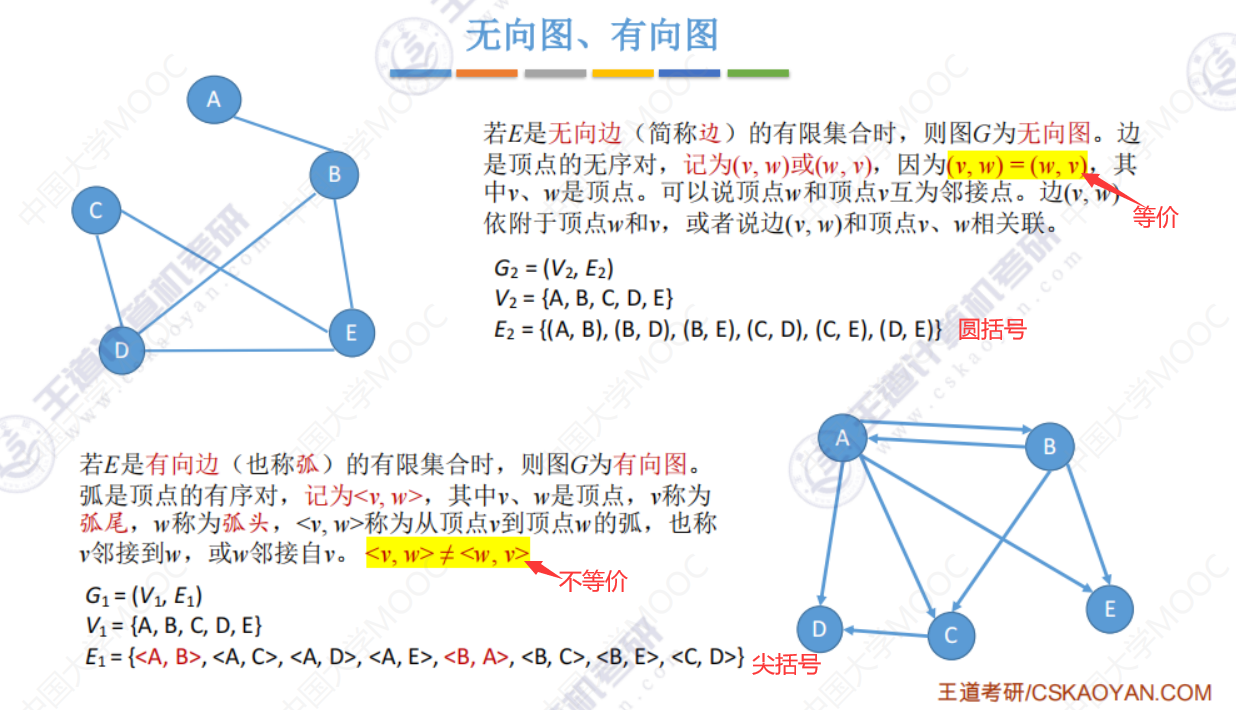
    在这里插入图片描述

    有向图、无向图

    没有箭头的那一段是弧尾，有箭头的那一段叫弧头。AE中A是弧尾，E是弧头。
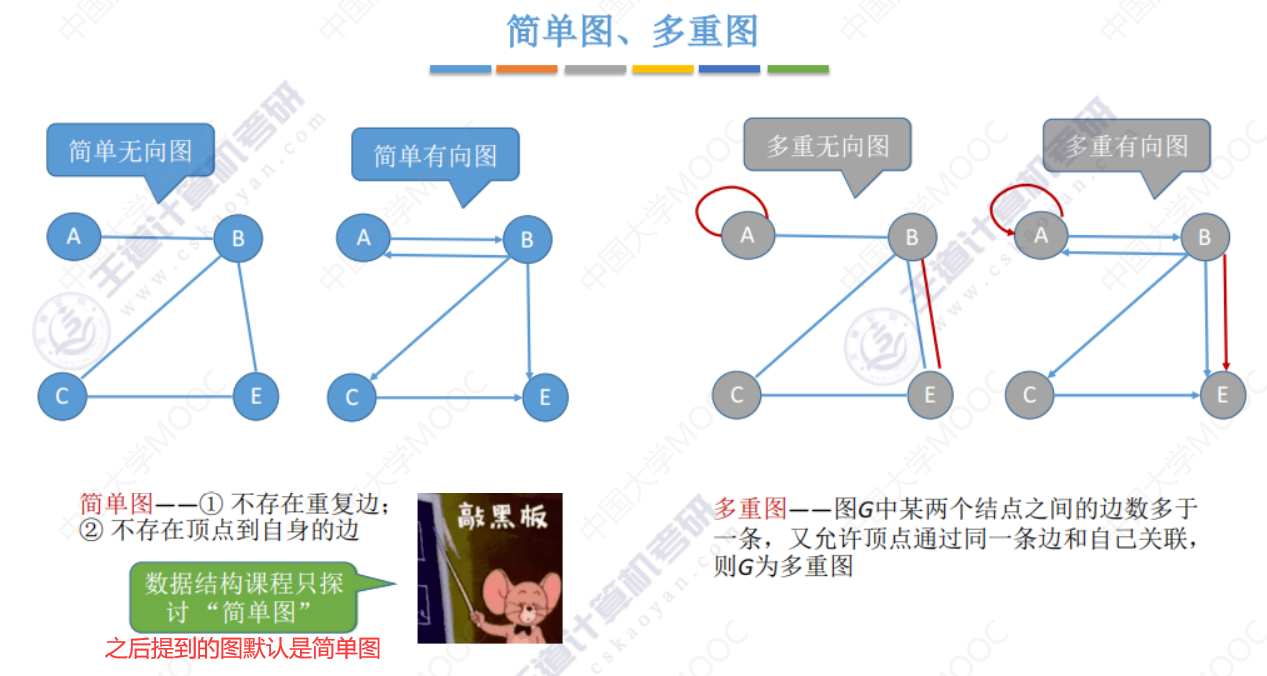
    在这里插入图片描述

    简单图、多重图

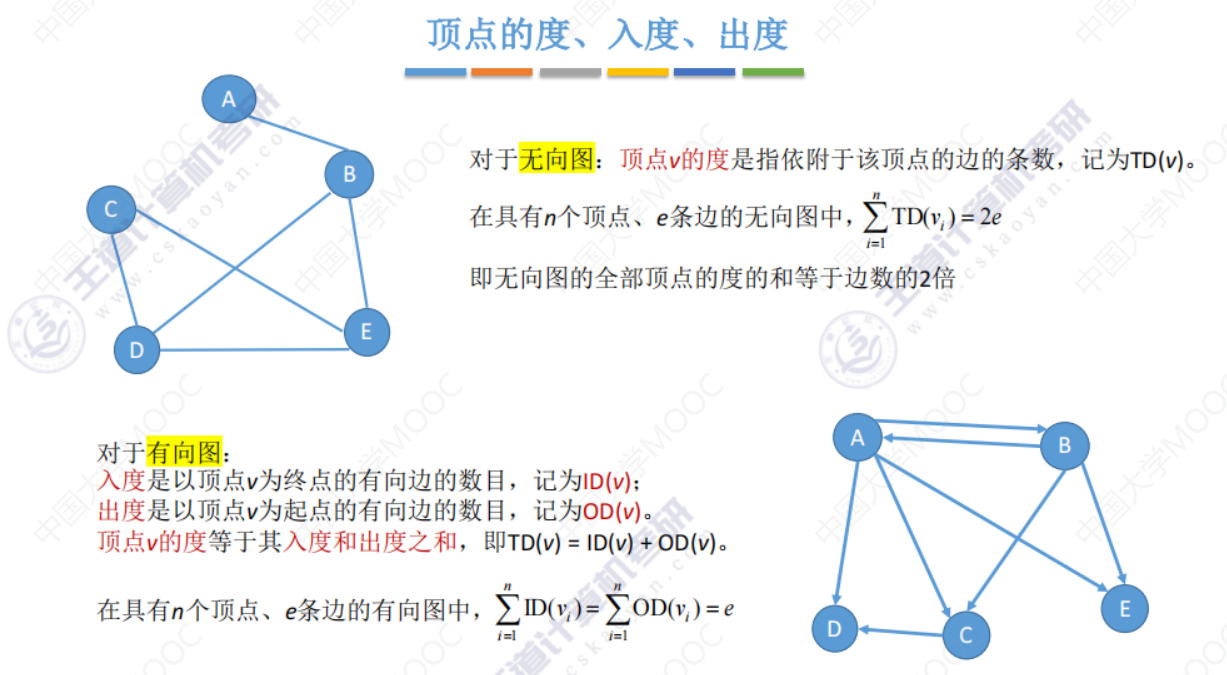
    在这里插入图片描述

    顶点的度、入度、出度

    在这里插入图片描述

    顶点-顶点的关系描述

    强连通就是正反都有路径，A和B是强联通的，A和E就不是强连通的
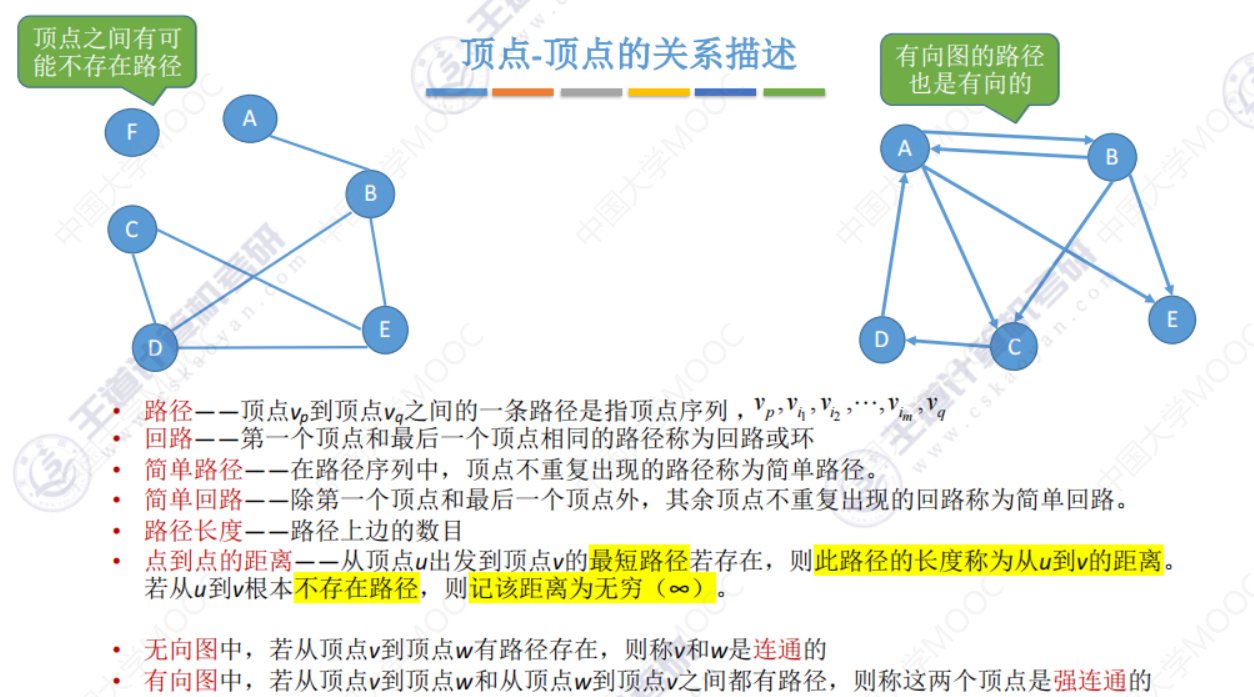
    在这里插入图片描述

    连通图、强连通图

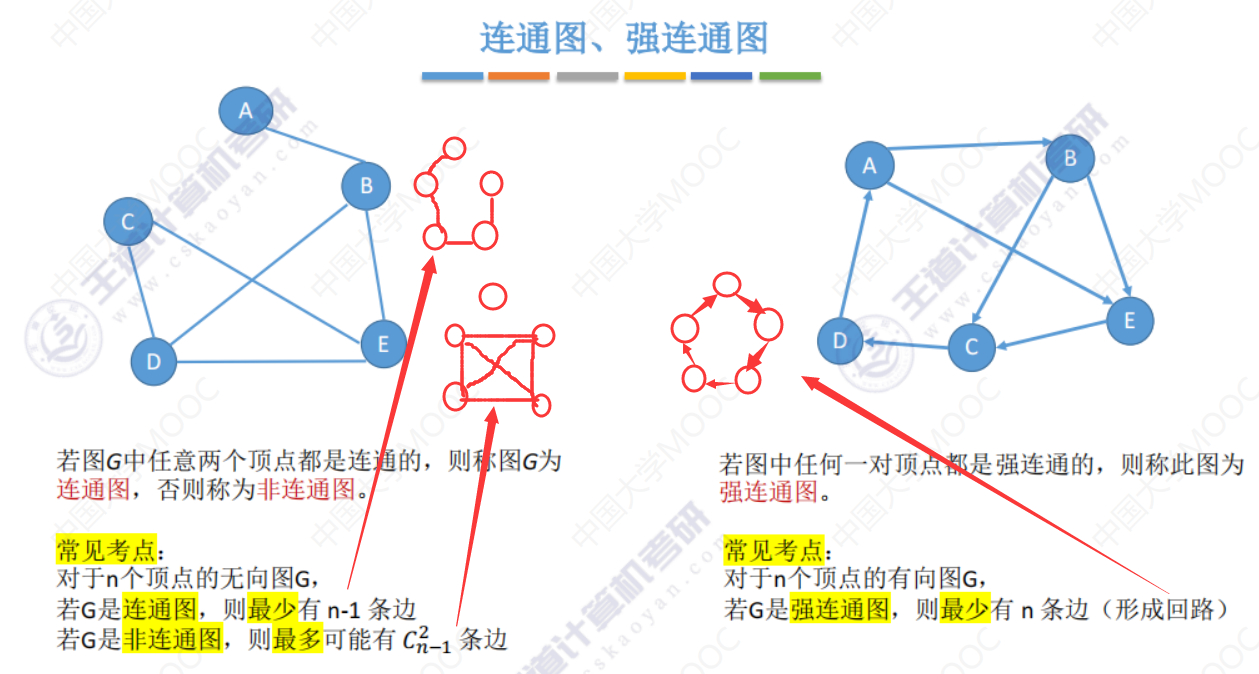
    在这里插入图片描述

    子图

    无向图

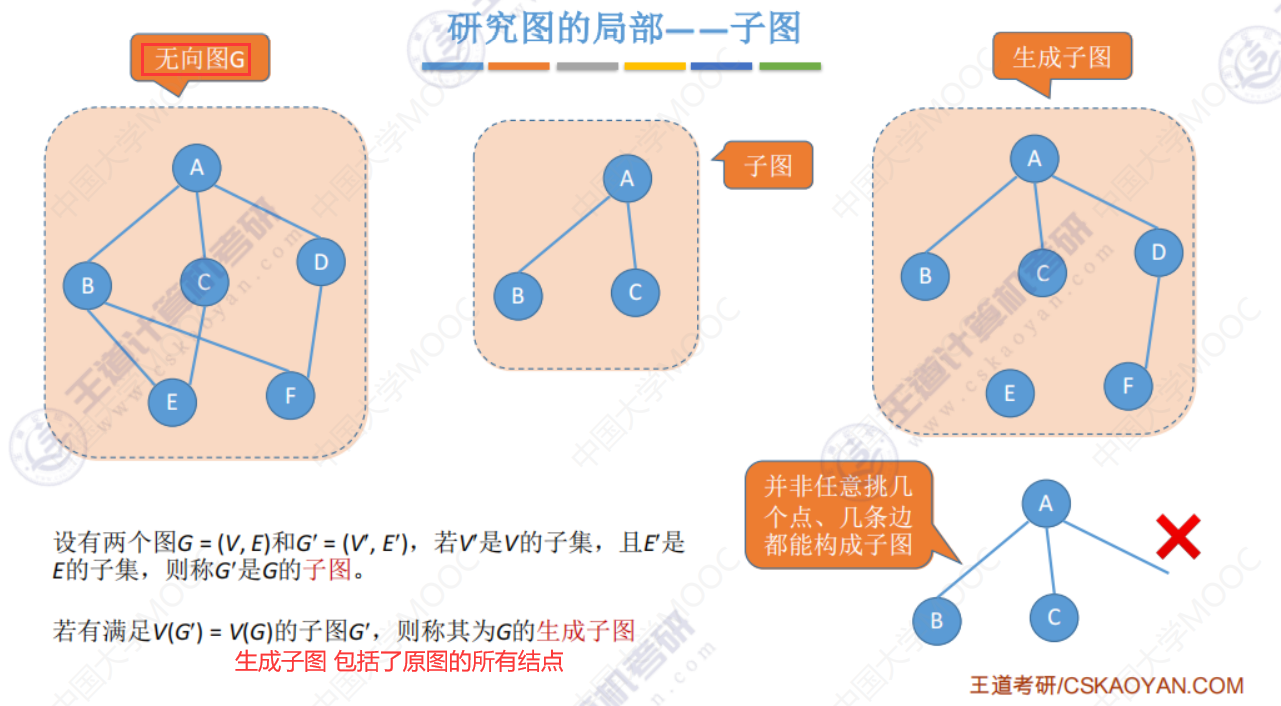
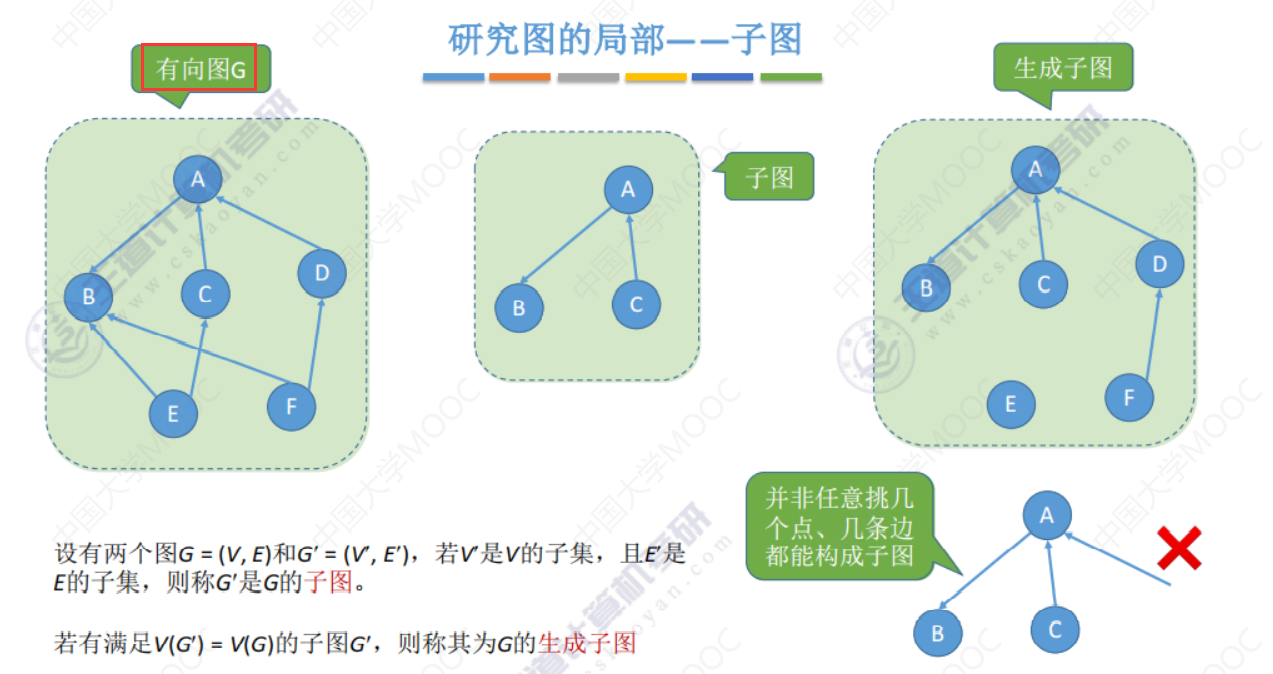
    在这里插入图片描述

    有向图（和上面无向图的定义相同）

    在这里插入图片描述

    连通分量（描述无向图的）

    极大连通子图是子图，且连通，且包含尽可能多的顶点和边
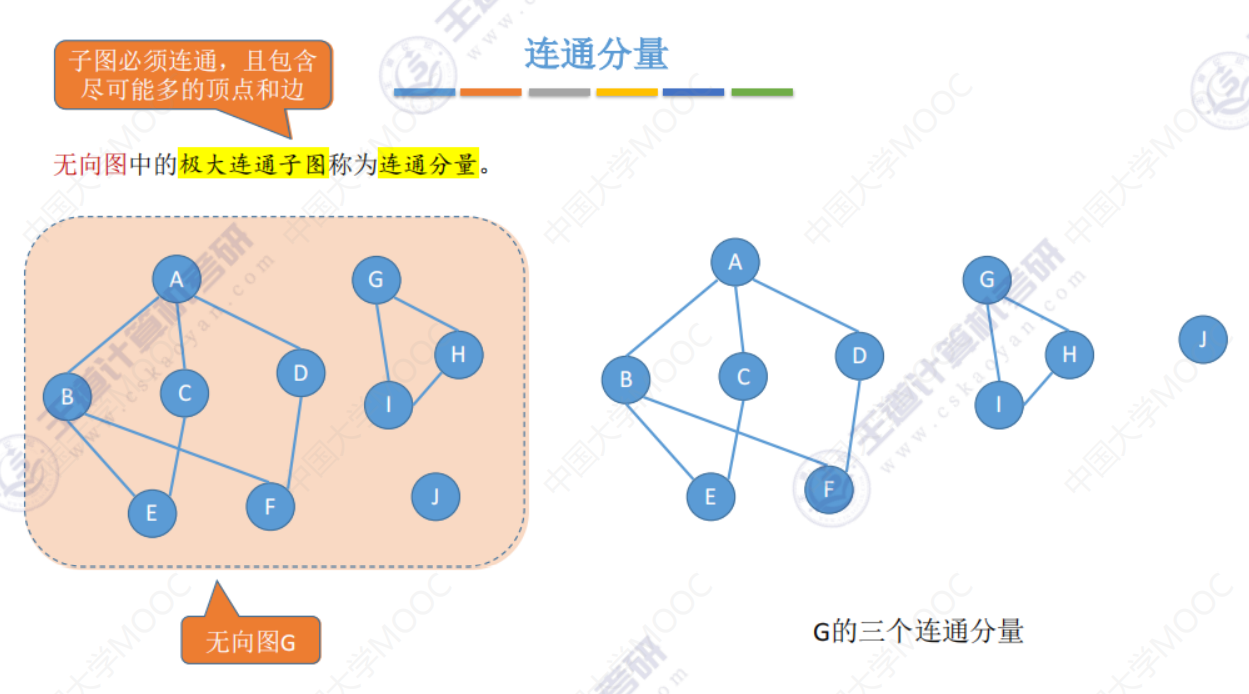
    在这里插入图片描述

    强连通分量（描述有向图的）

    有向图中的 极大强连通子图 称为有向图的 强连通分量（极大强连通子图是强连通分量）
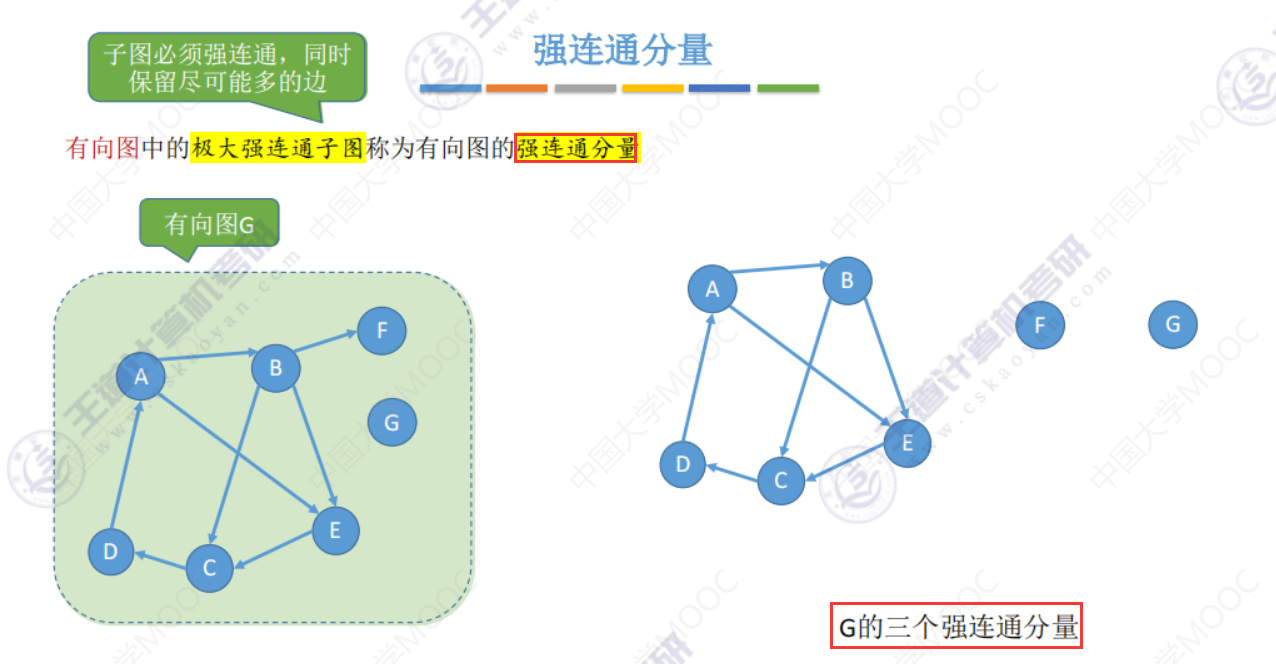
    在这里插入图片描述

    生成树

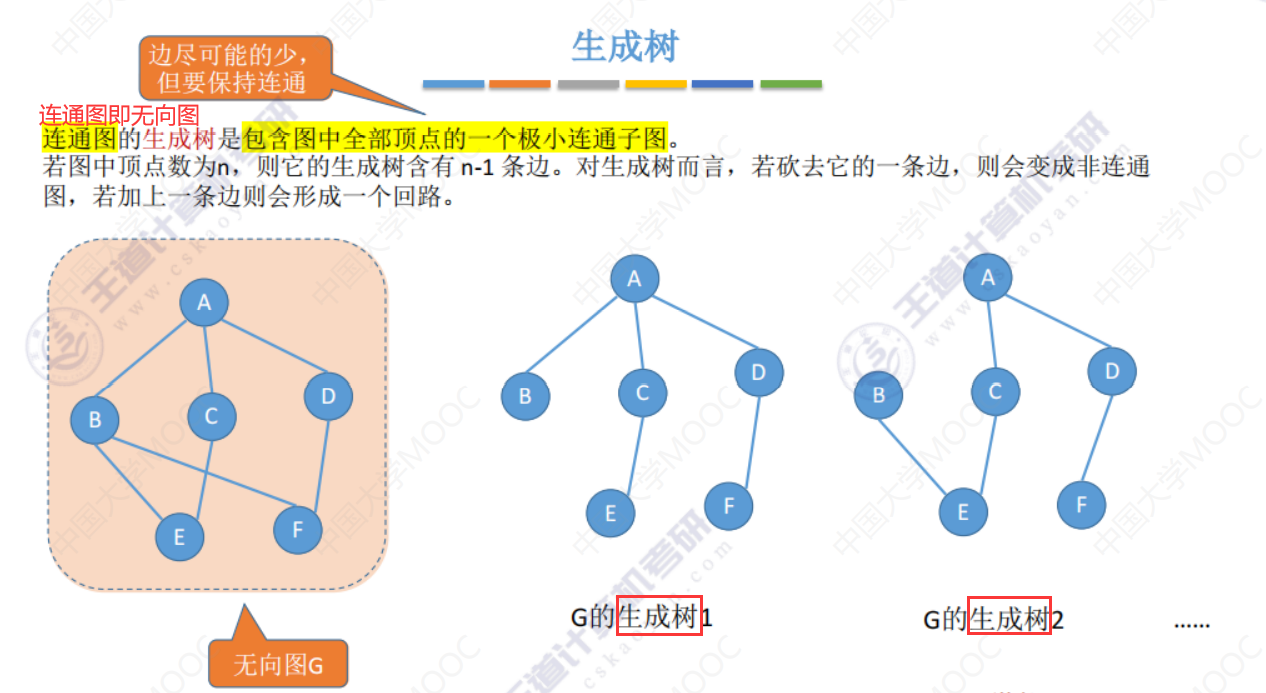
    在这里插入图片描述

    生成森林

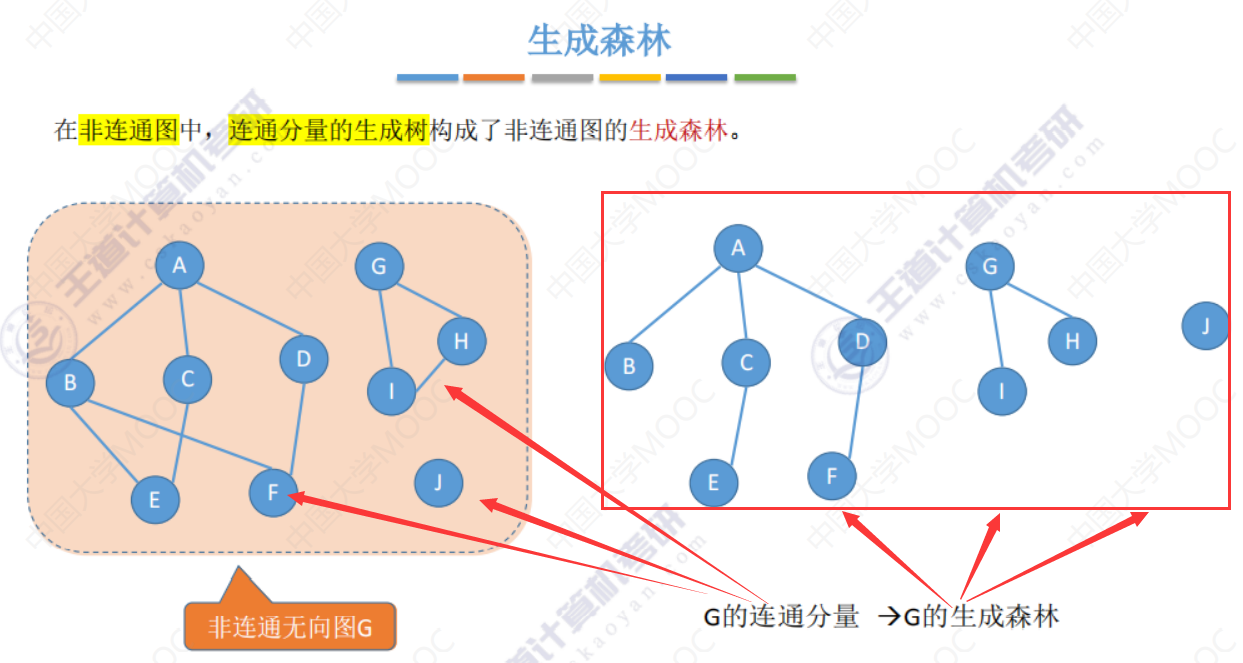
    在这里插入图片描述

    边的权、带权图/网

    北京到上海的带权路径长度是200+600=800
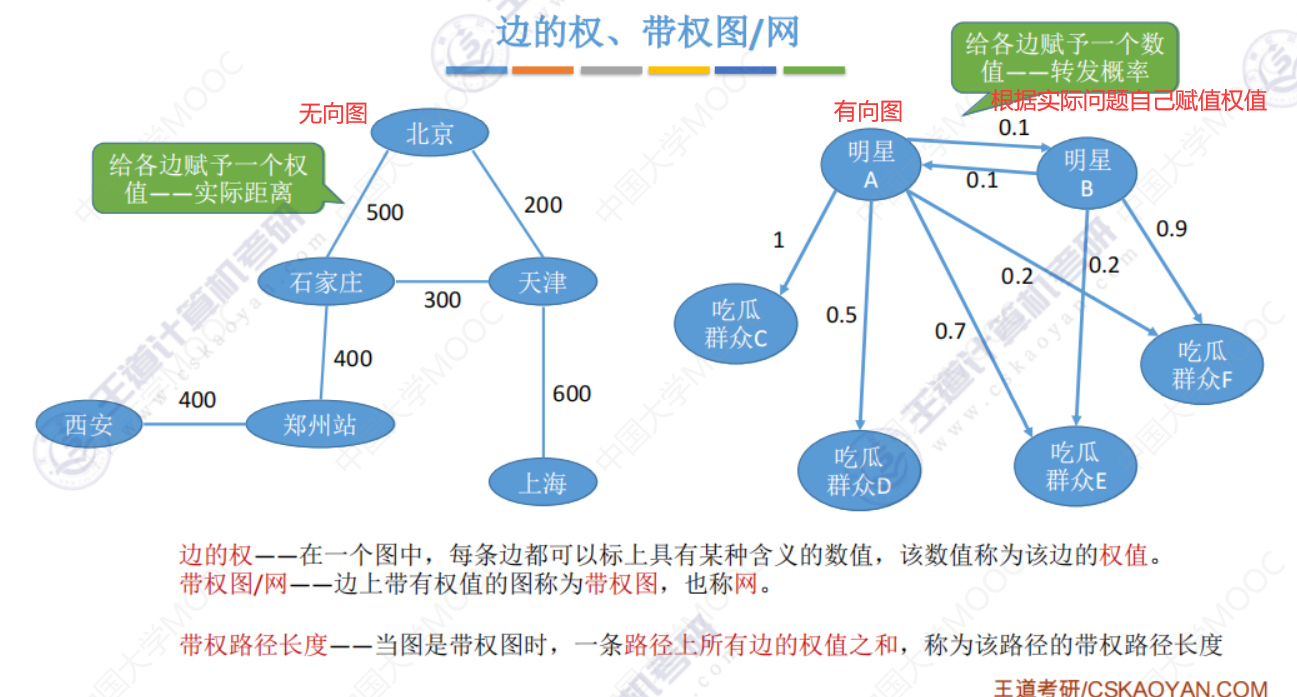
    在这里插入图片描述

    几种特殊形态的图

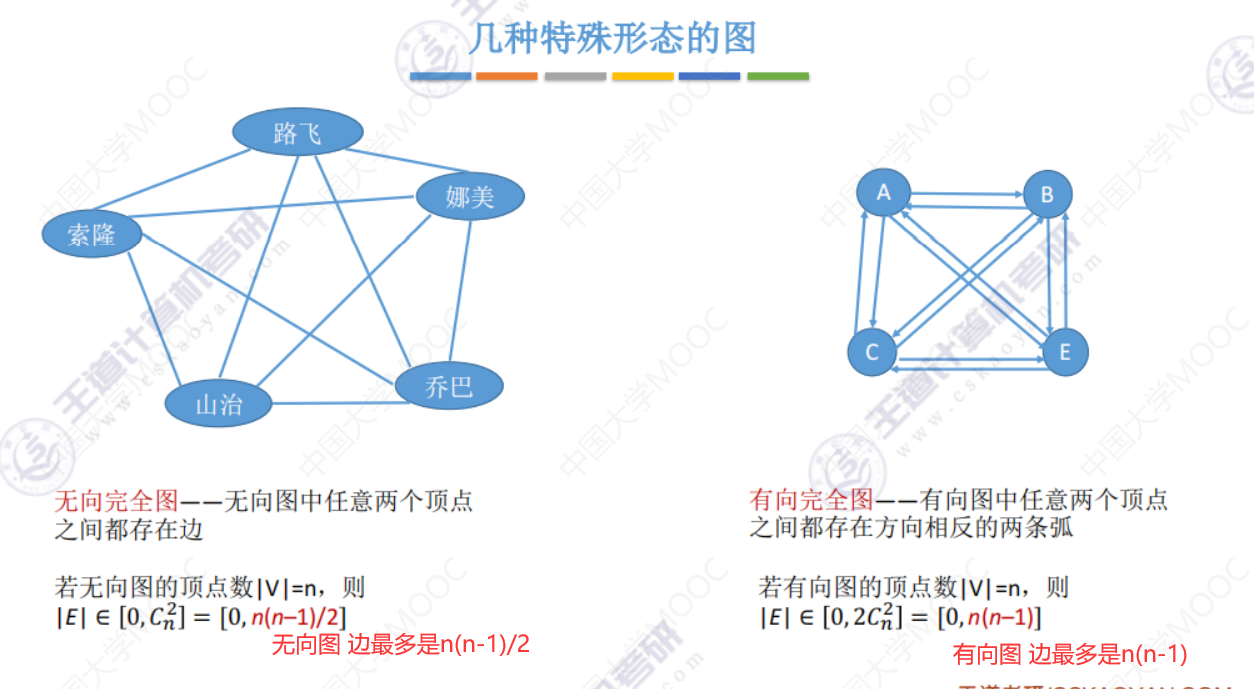
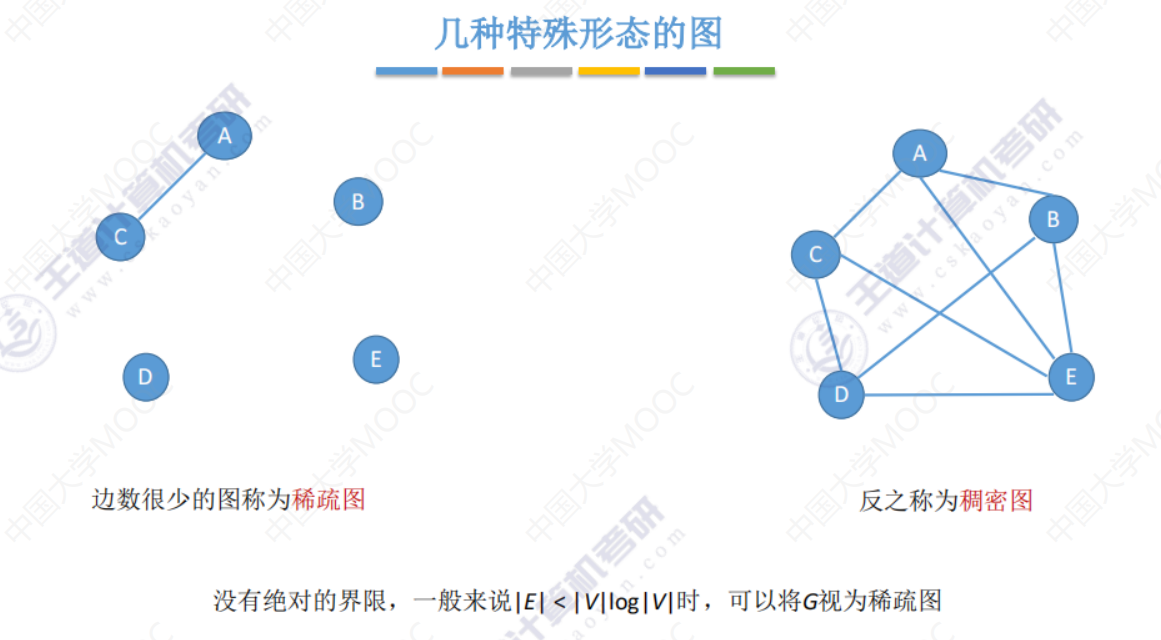
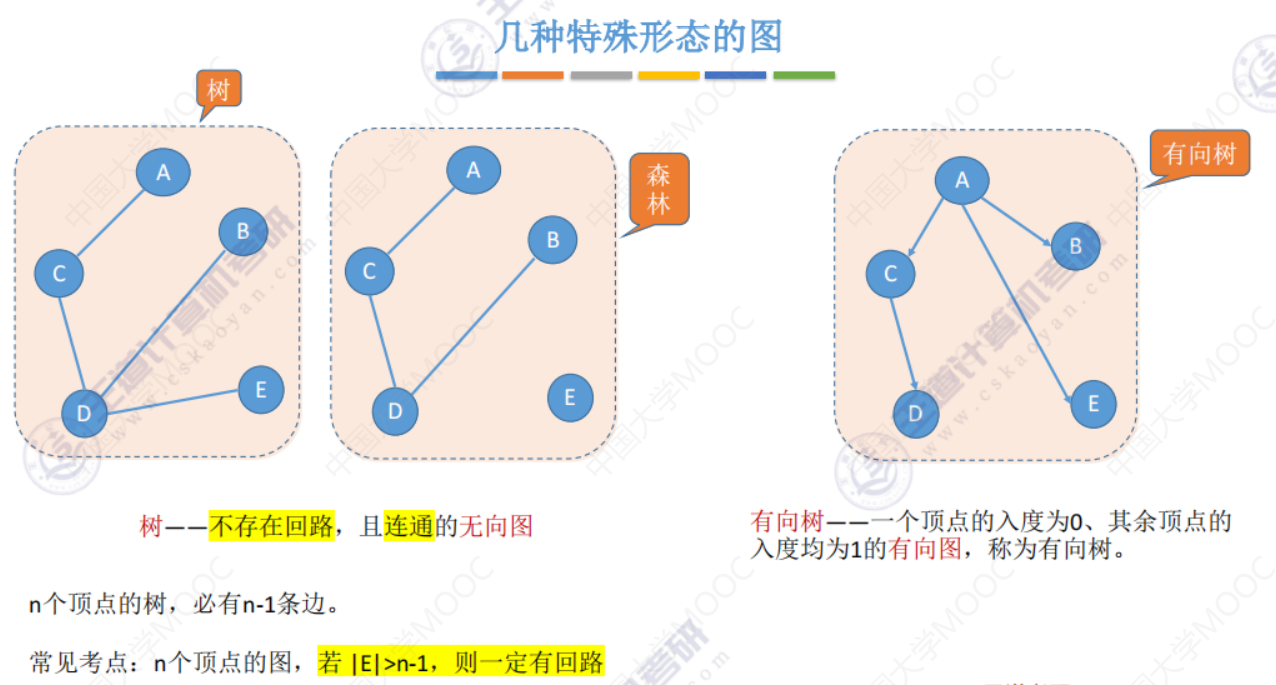
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    n个顶点的连通图最少有n-1条边，如果在多一条边，一定有回路。

    6.2-1 邻接矩阵法（数组实现的顺序存储，空间复杂度高，不适合存储稀疏图）

    0表示不连接，1表示连接。
    Vex数组中存储A,B,C,D,E,F,
    然后在Edge中对应数组下标0，1，2，3，4，5，
    这样我们表示AB这条边 就可以用Edge[0][1]=1来表示了。
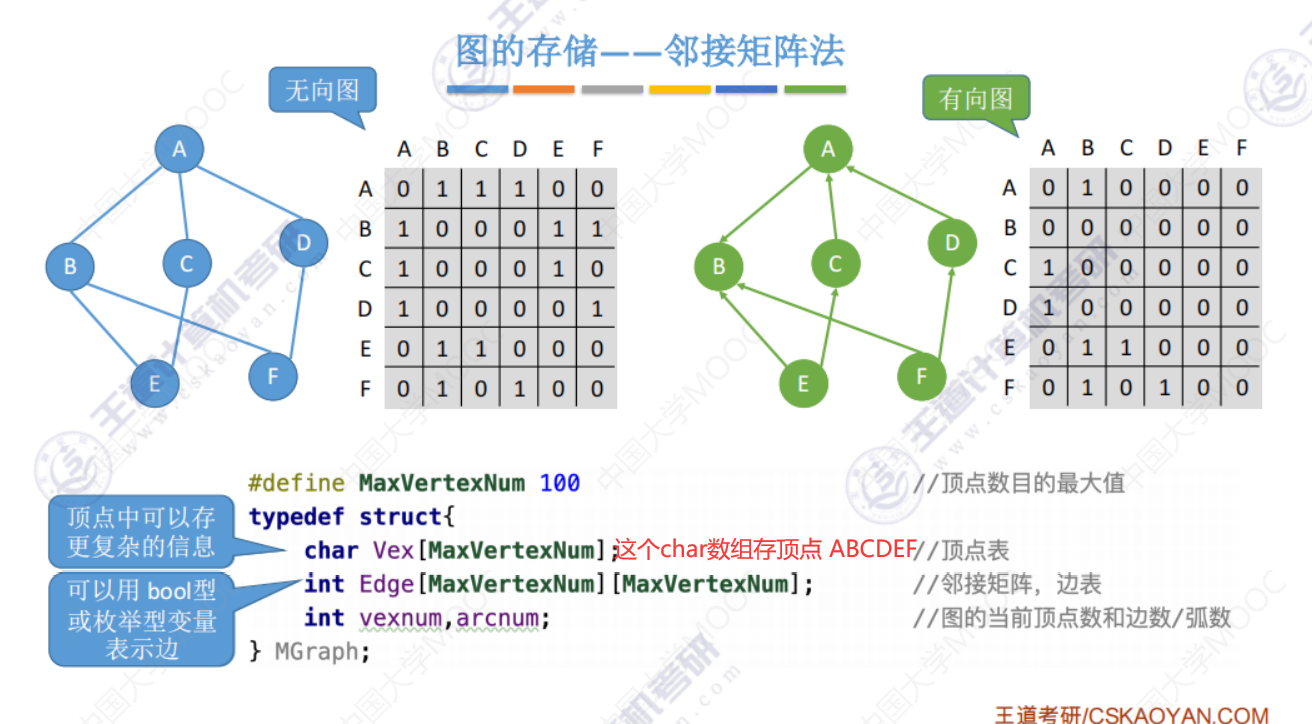
    在这里插入图片描述
    因为Edge数组中只存0、1，且bool类型只占1个字节，比int类型占4个字节 占用的空间少，所以可以考虑使用bool类型表示边。

    邻接矩阵存储 不带权 的图

    下图中的（vi，vj）中的v是上图中的char型名为Vex的数组。
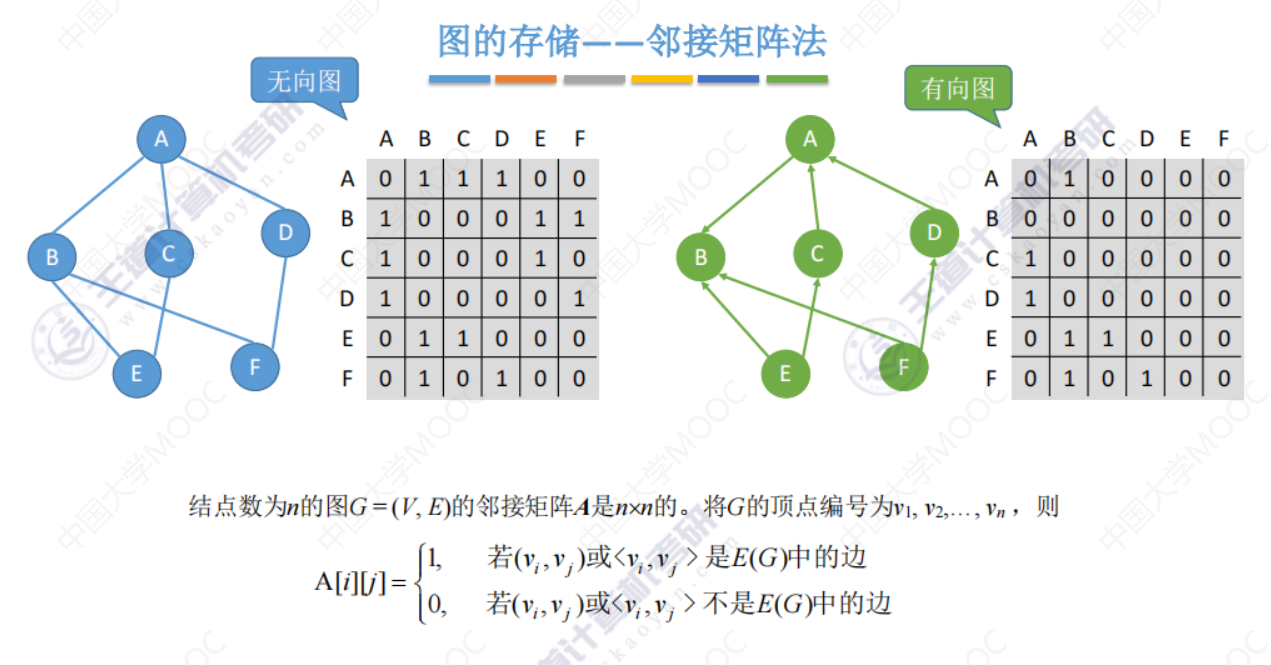
    在这里插入图片描述
    在这里插入图片描述

    邻接矩阵存储 带权 图

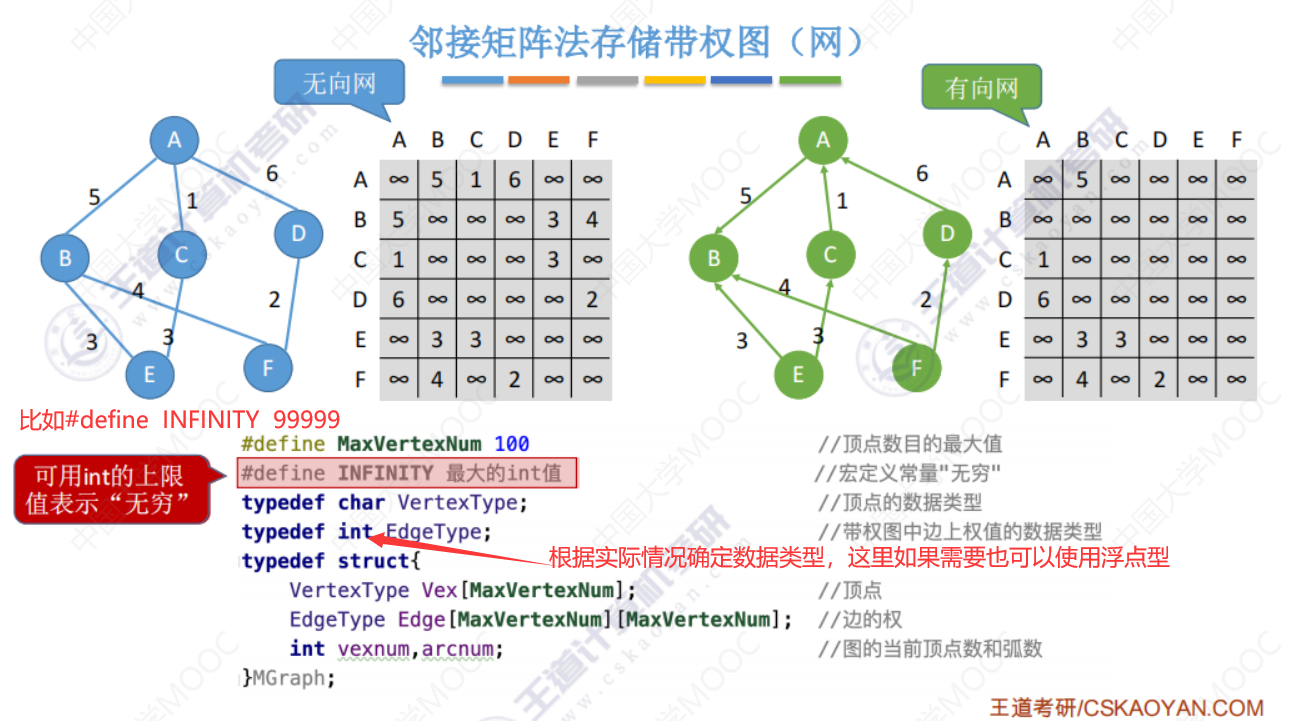
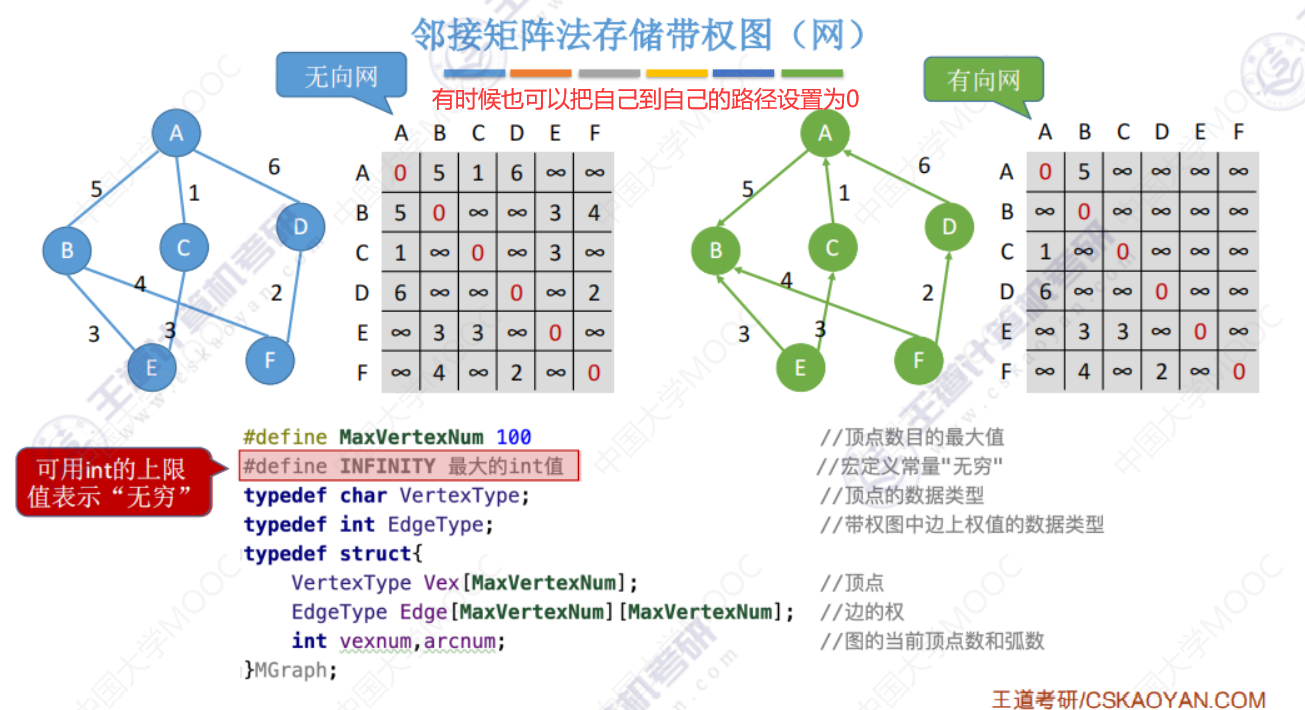
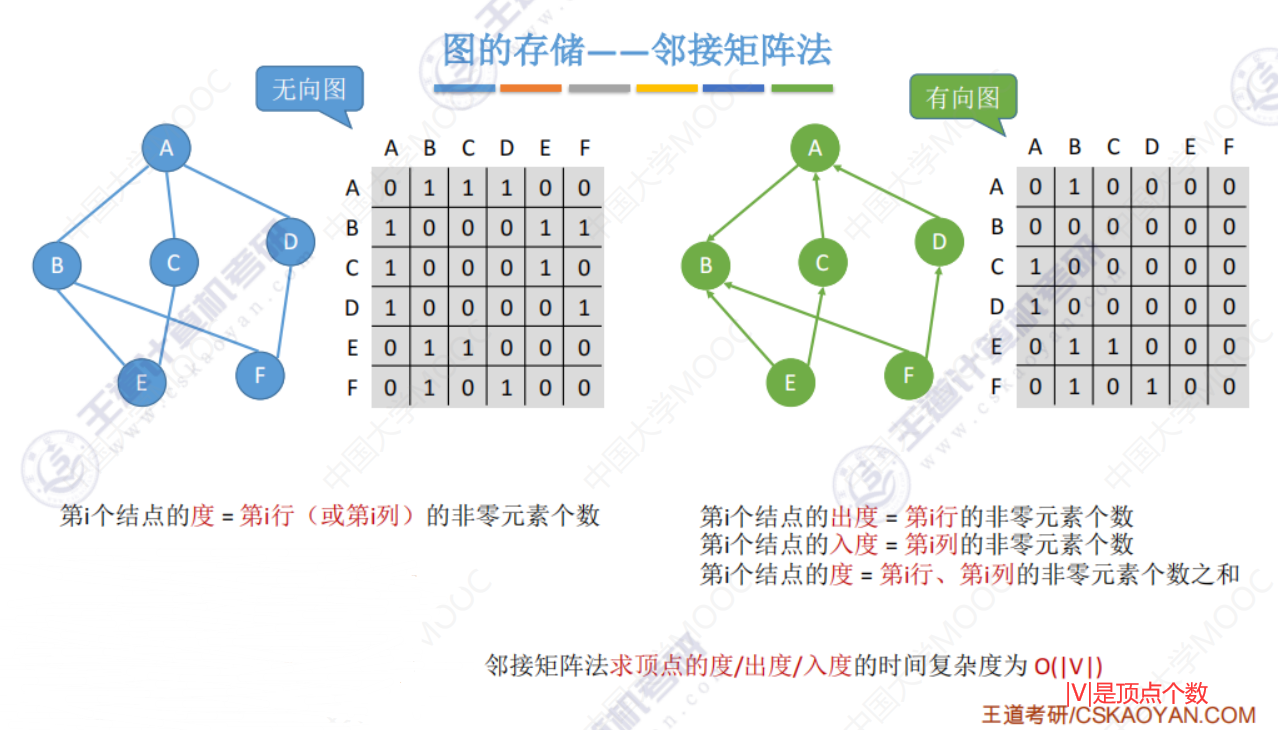
    在这里插入图片描述
    在这里插入图片描述

    邻接矩阵法的性能分析

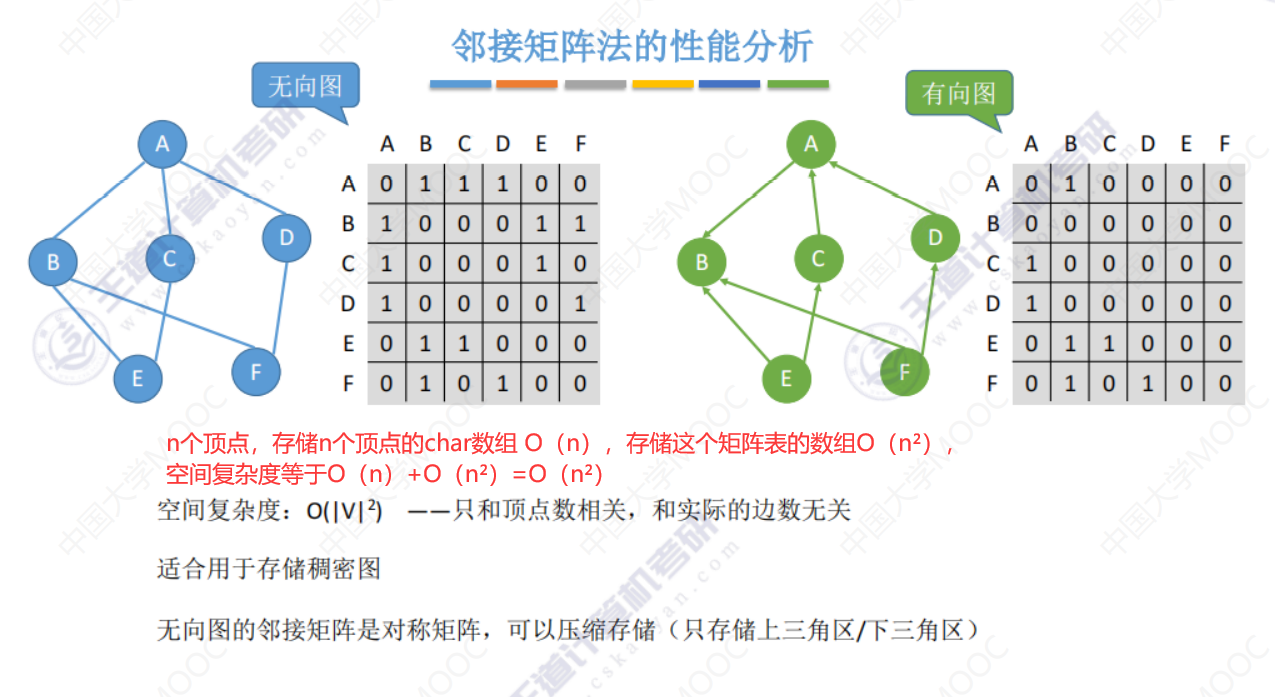
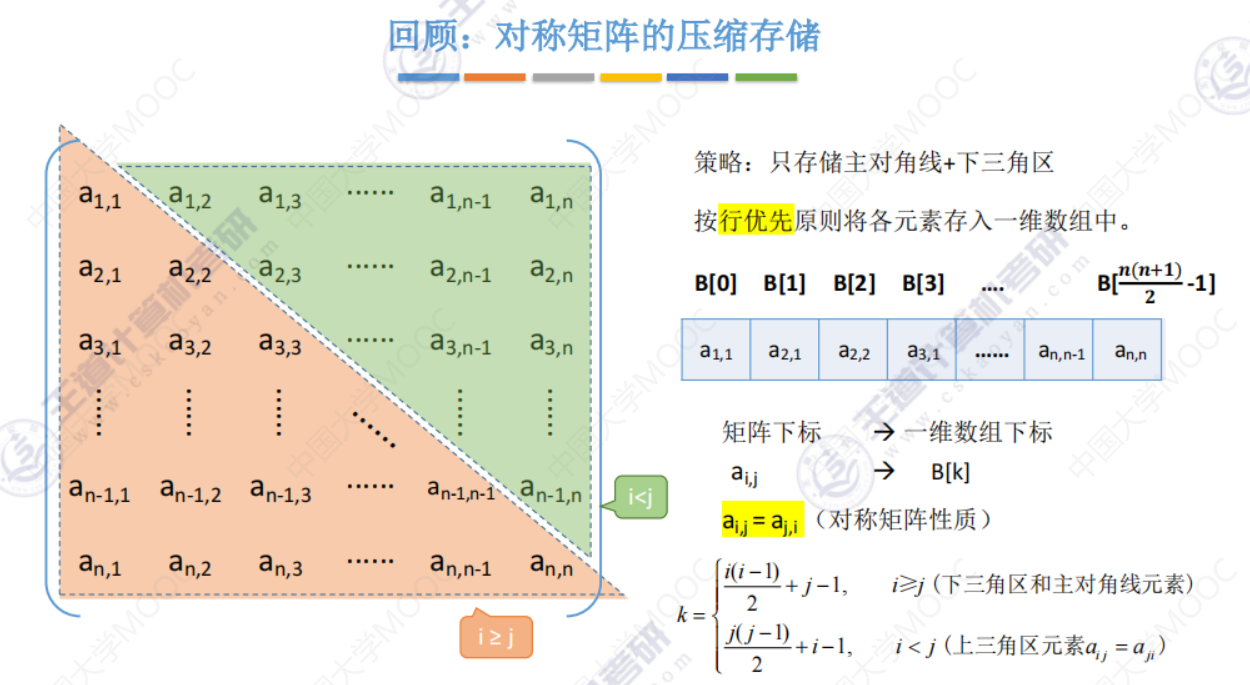
    在这里插入图片描述
    在这里插入图片描述

    邻接矩阵法的性质

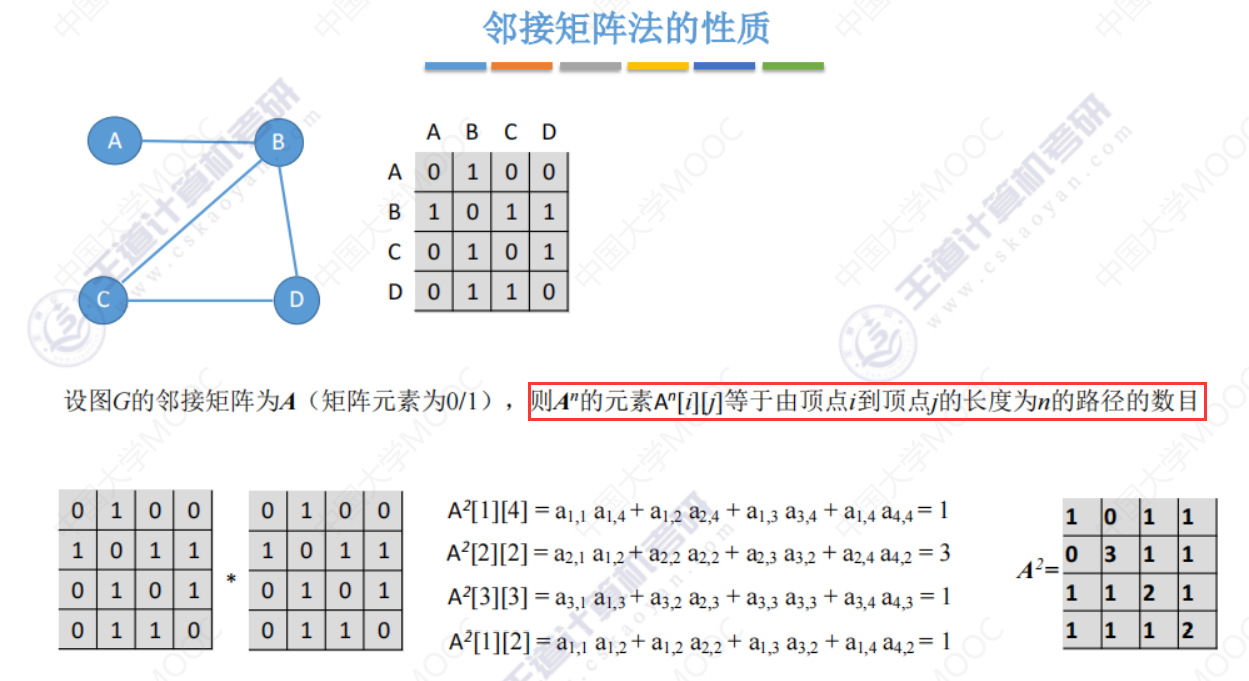
    在这里插入图片描述

    矩阵相乘

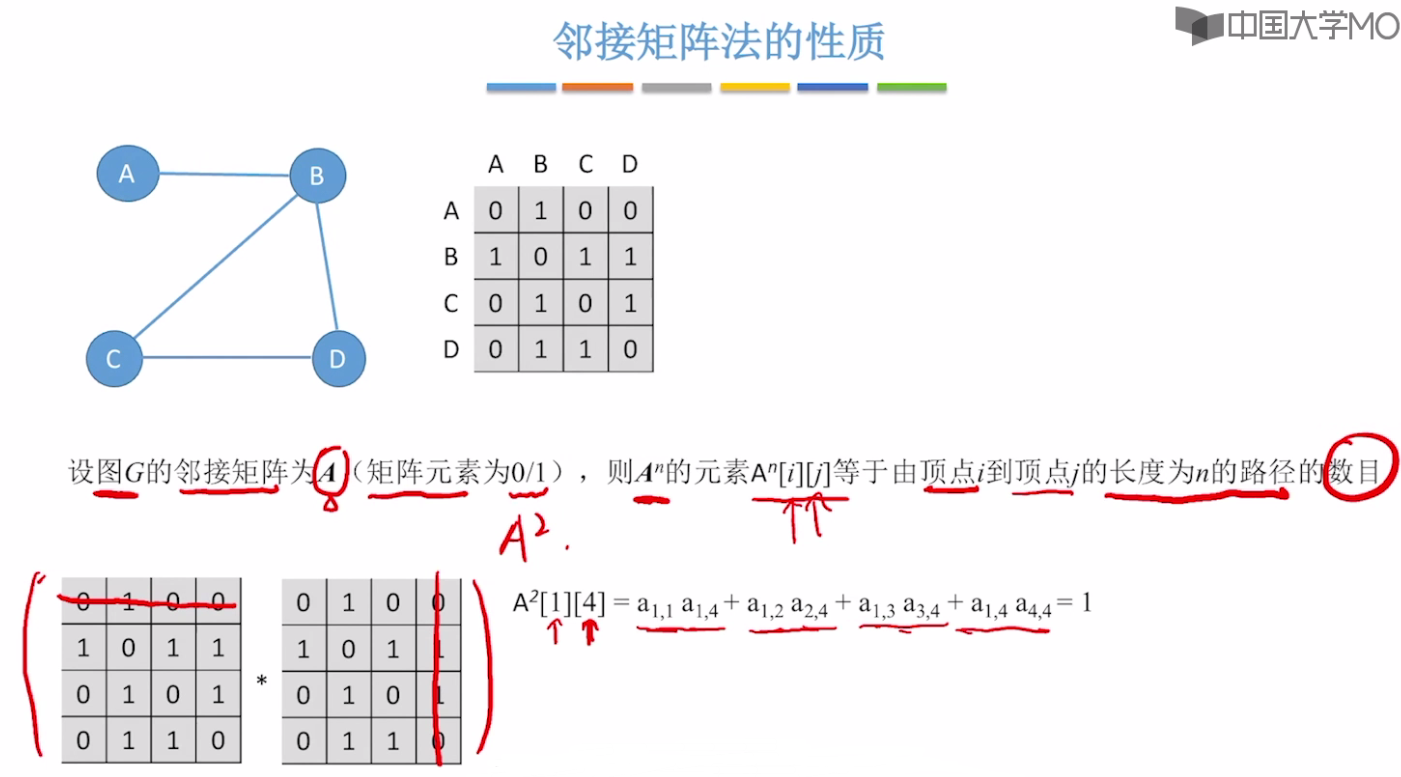
    在这里插入图片描述

    从顶点1到顶点4的长度为2的路径的数目为1

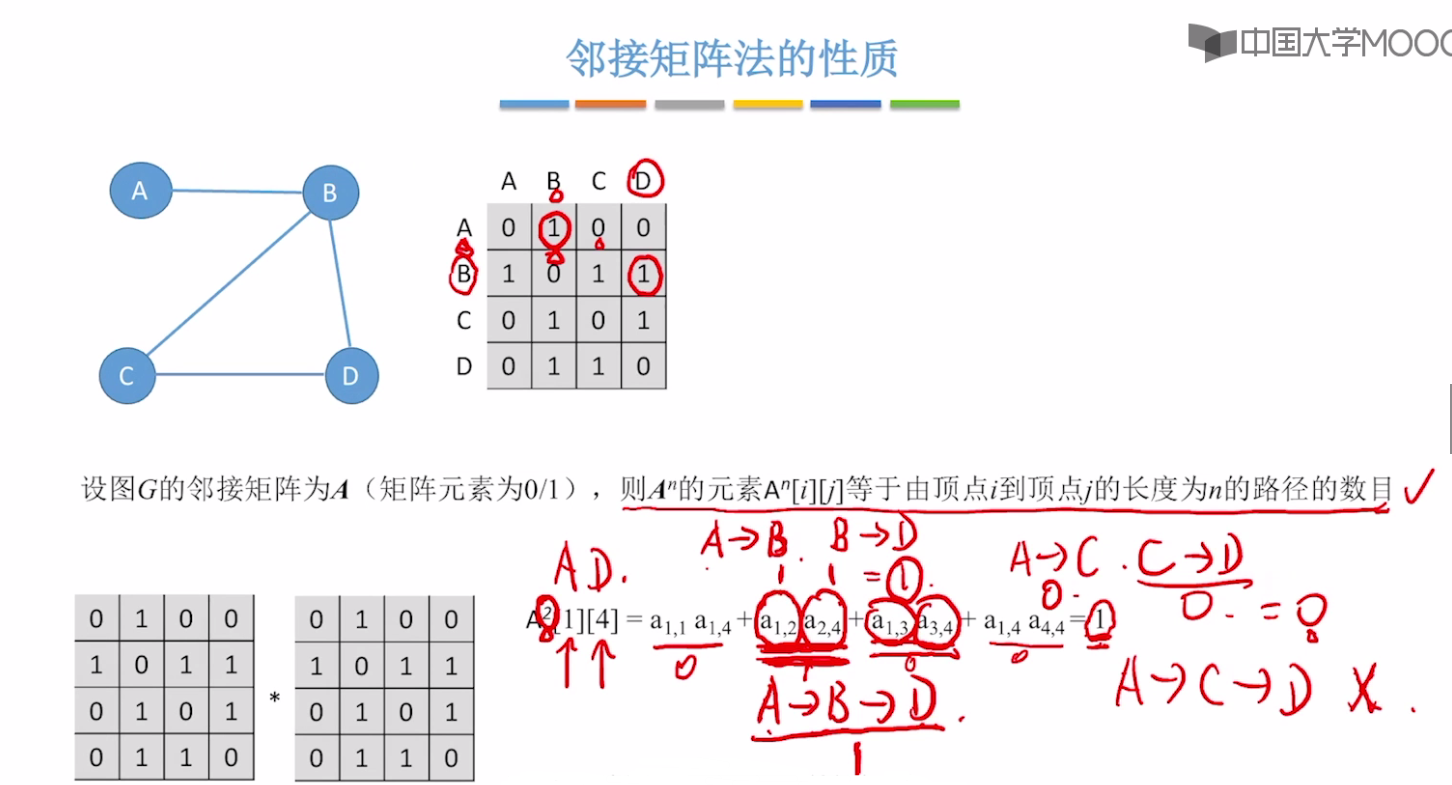
    在这里插入图片描述

    6.2-2 邻接表法（顺序+链式存储）

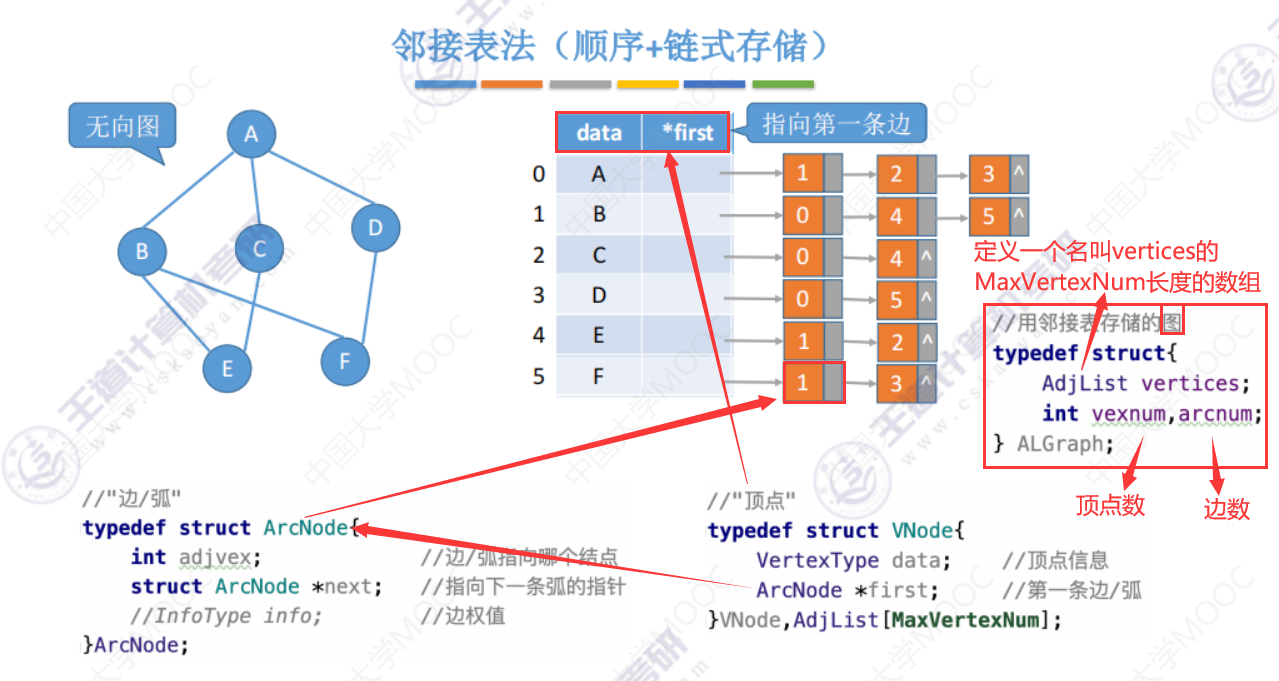
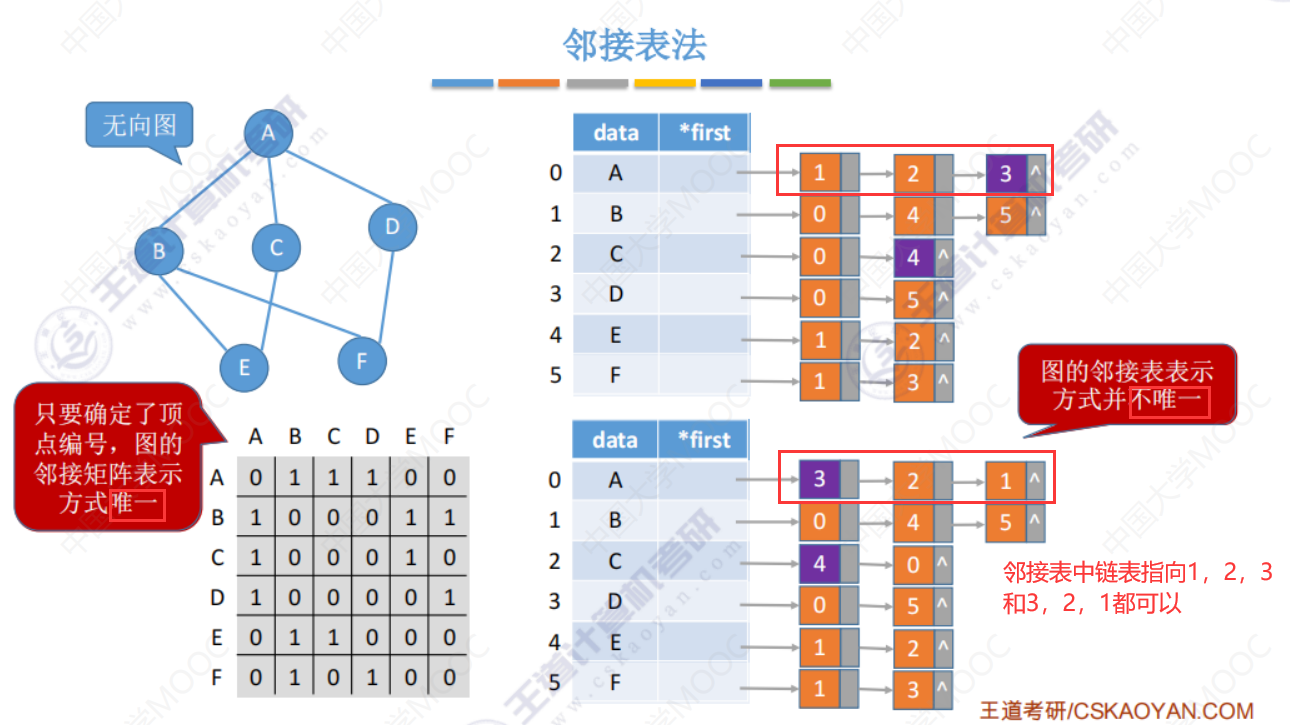
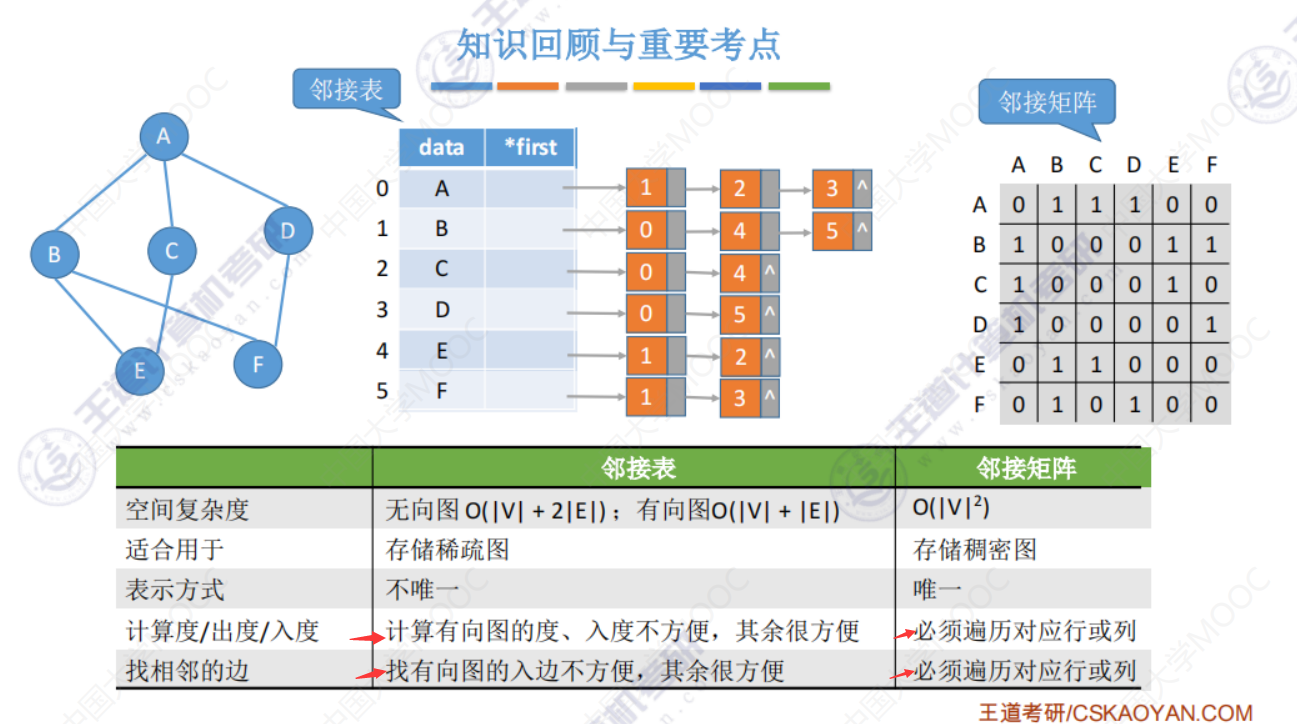
    在这里插入图片描述
    无向图中：边会被链表使用两次，所以边结点的数量是2|E|，整体空间复杂度是O(|V|+2|E|).
    无向图中度就是遍历对应结点的链表就行了。
    有向图中：求出度容易，直接遍历对应结点的链表就行了，找 出边也容易，如果求入度、度、入边，那么需要遍历整个表才行。
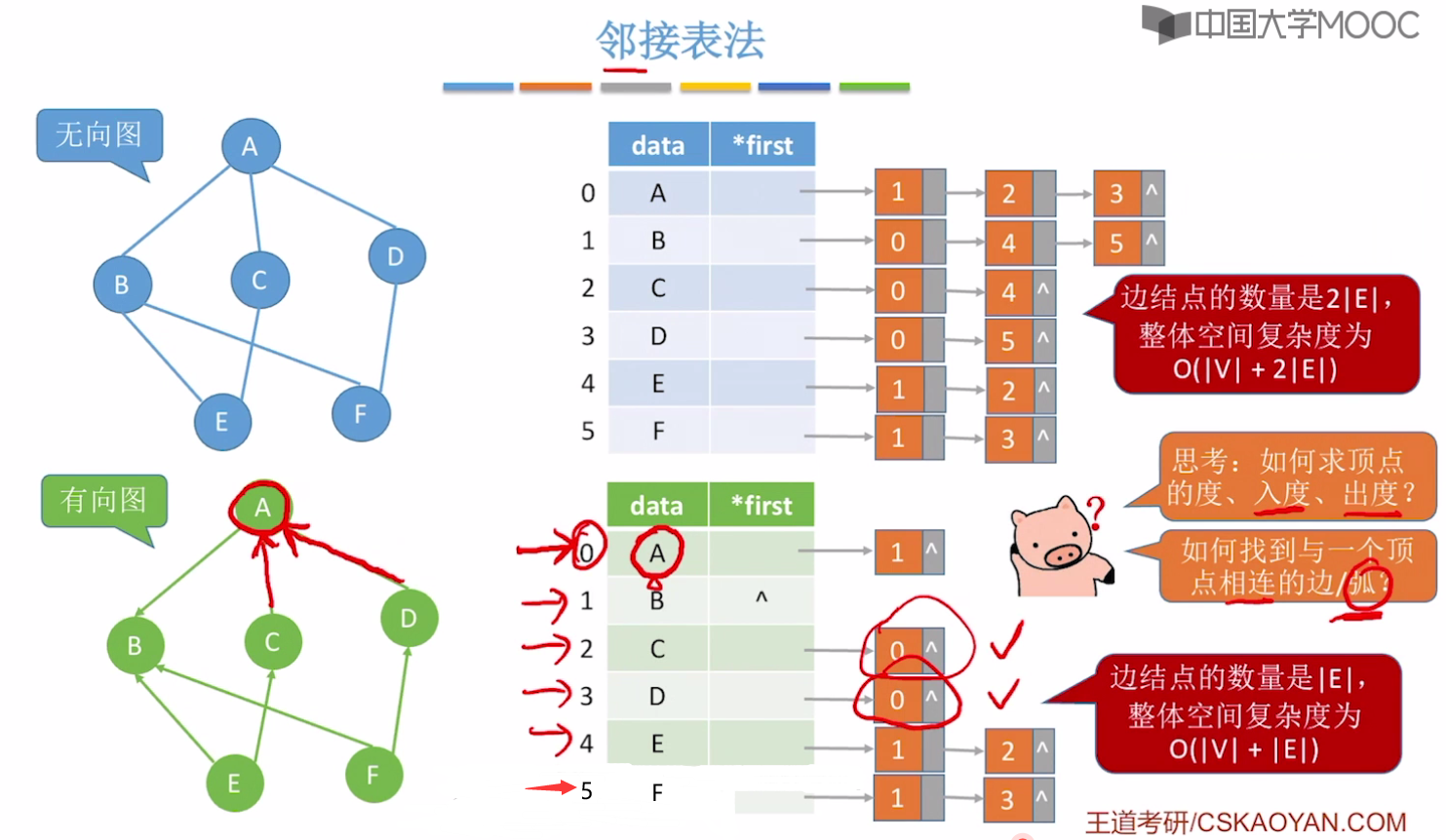
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述

    6.2-3 十字链表、邻接多重表

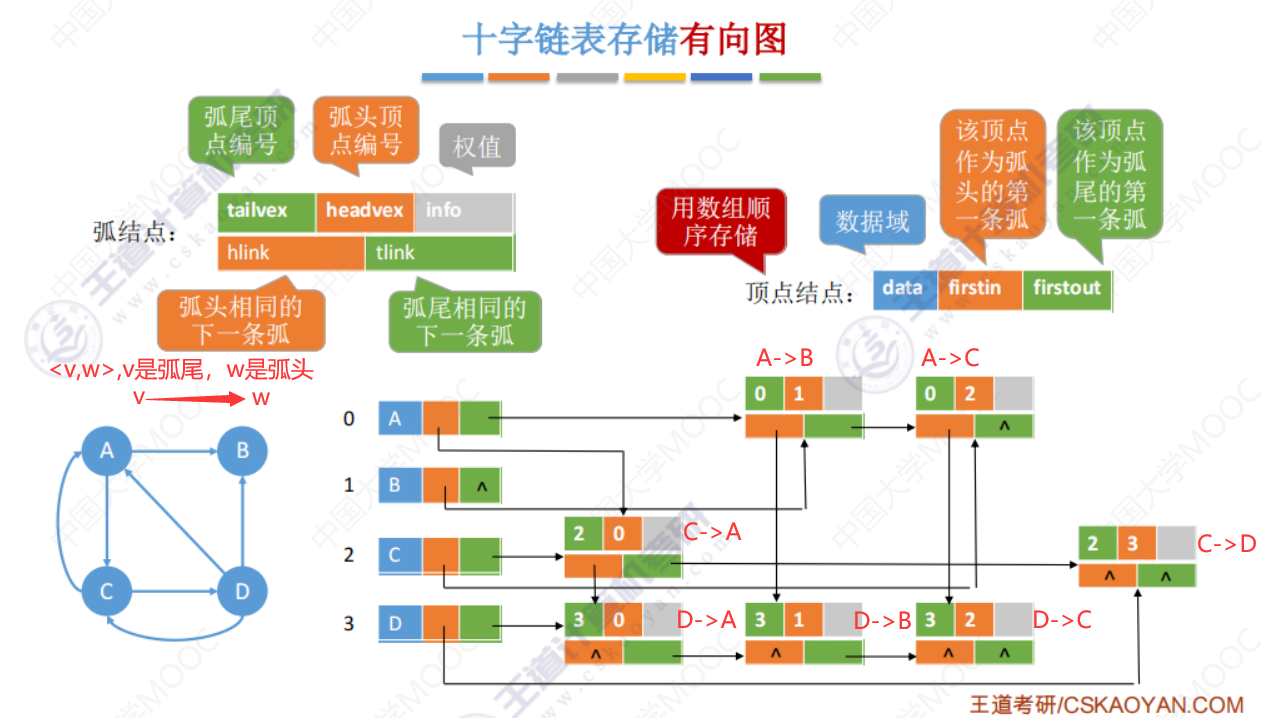
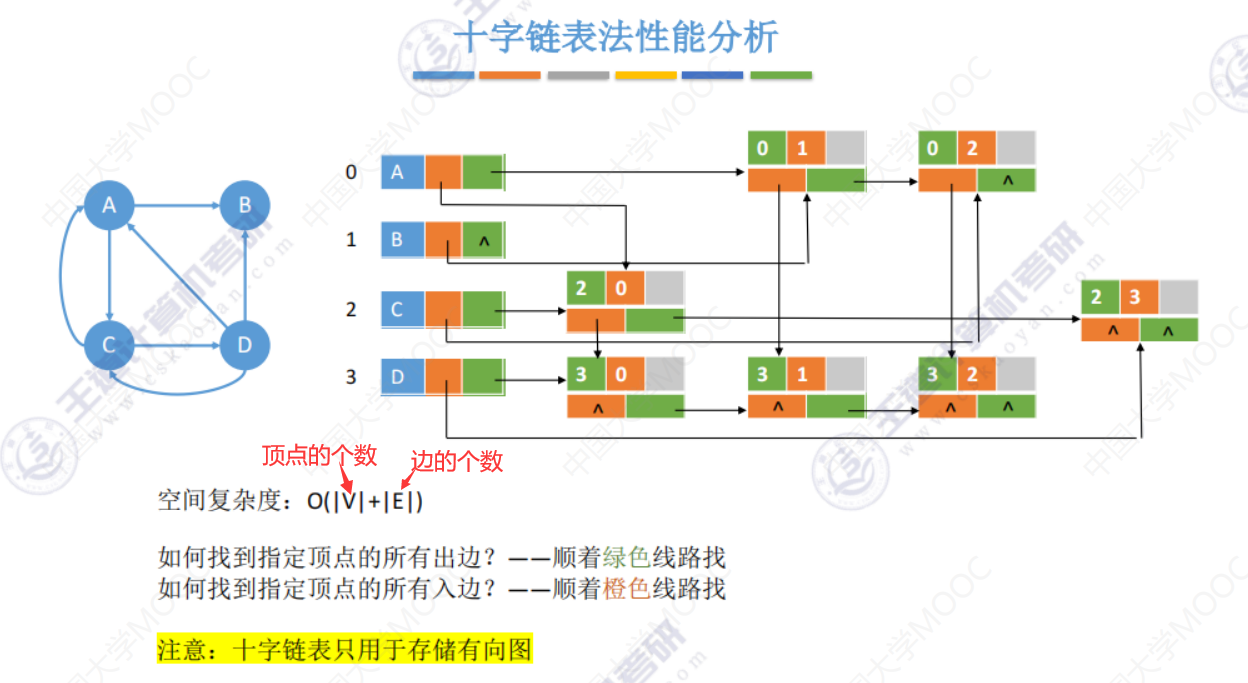
    十字链表（存储有向图）

    十字链表法解决了有向图 找入边 不方便问题。

    橙色连接了弧头相同的弧，绿色连接了弧尾相同的弧。
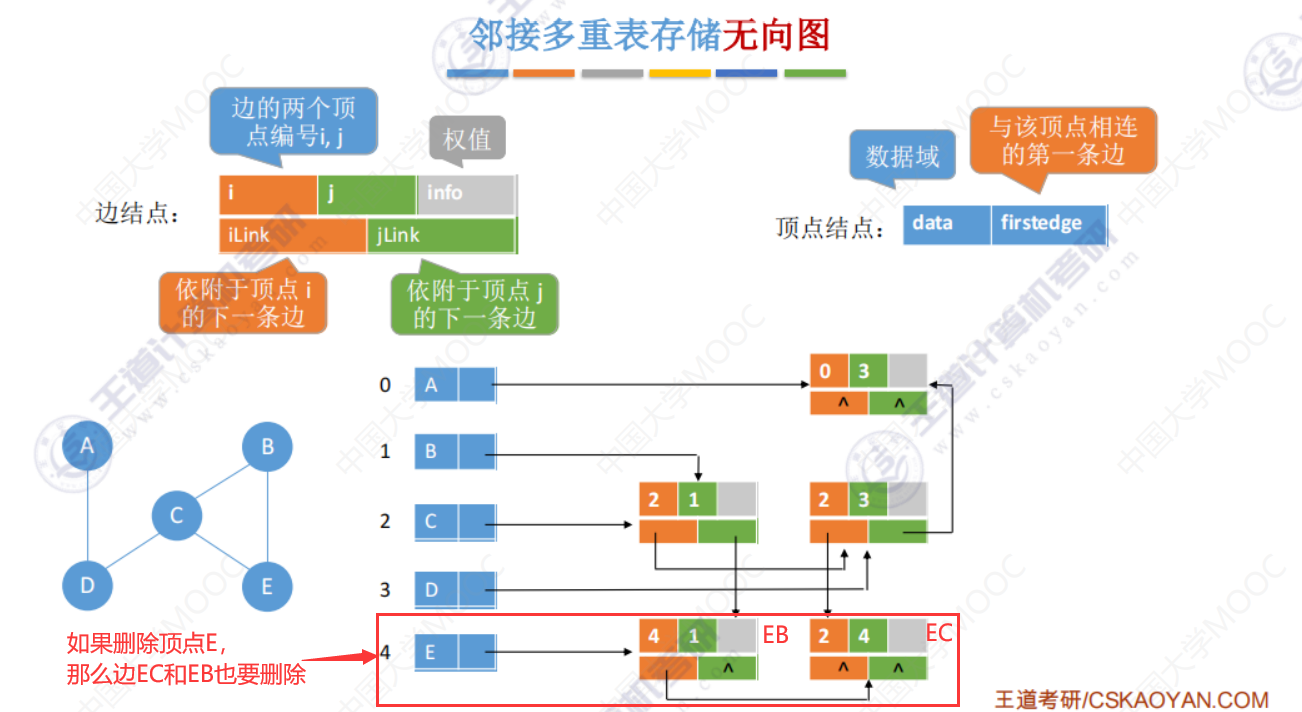
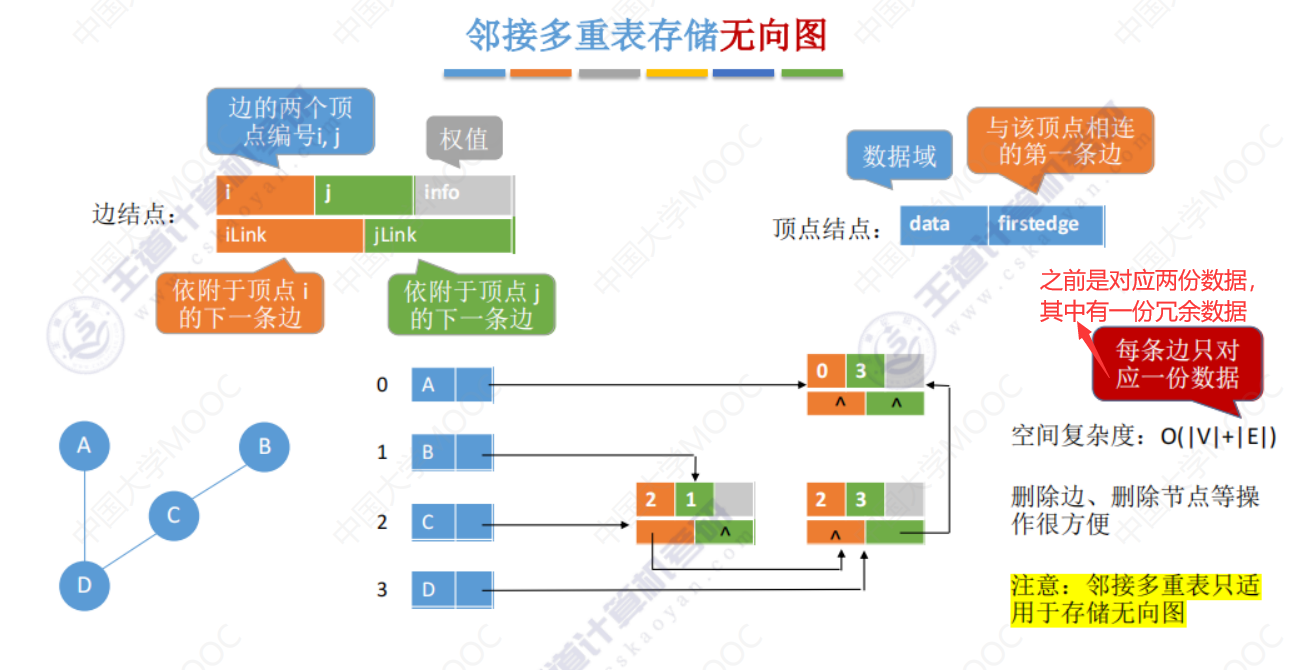
    在这里插入图片描述
    在这里插入图片描述

    邻接多重表（存储无向图）

    邻接矩阵、邻接表 存储无向图的缺点

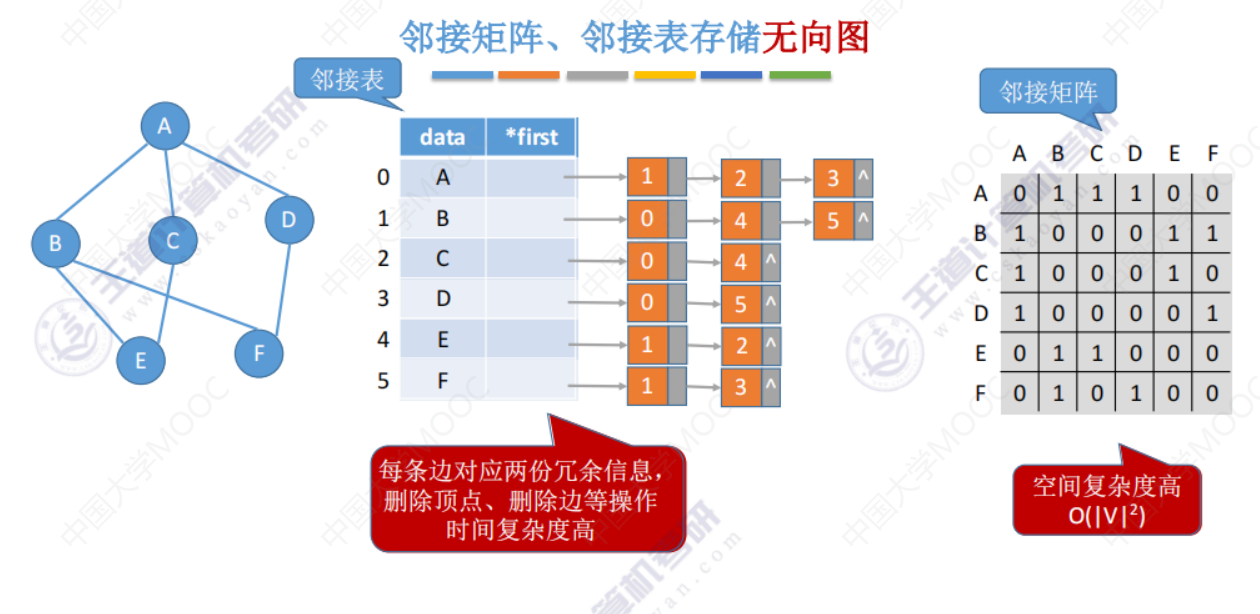
    在这里插入图片描述

    邻接多重表 存储无向图

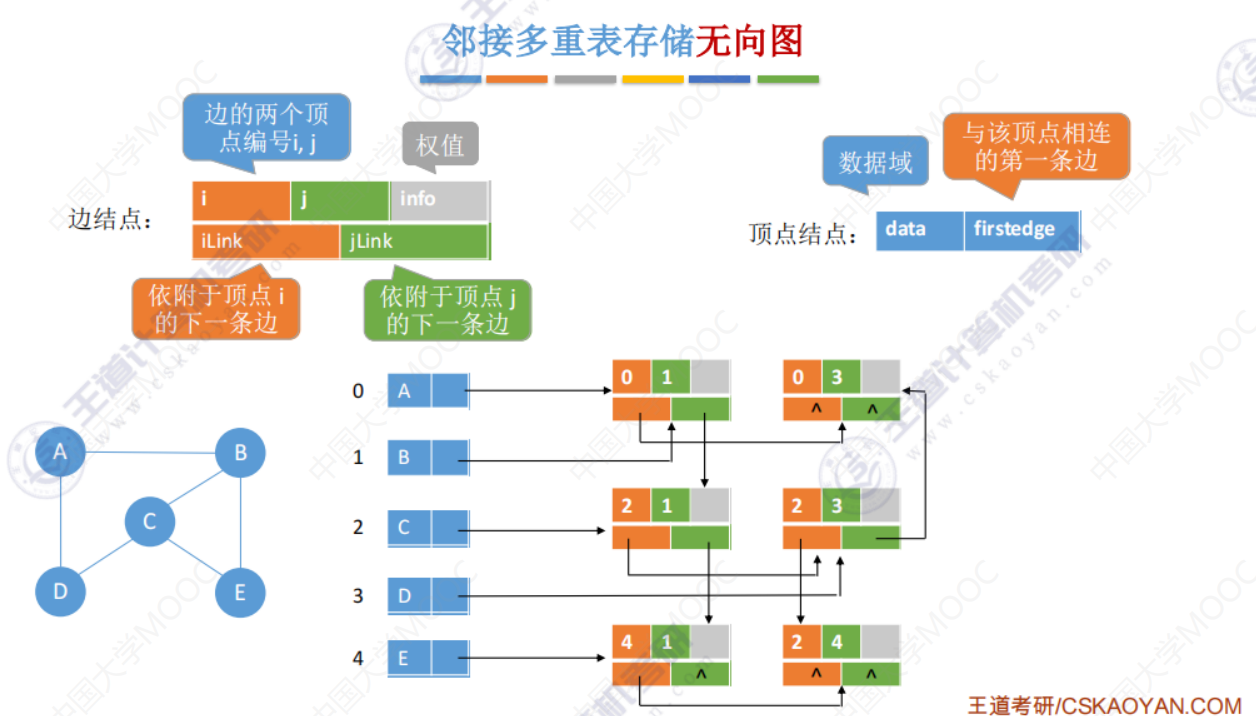
    在这里插入图片描述

    两个删除操作

    删除一条边

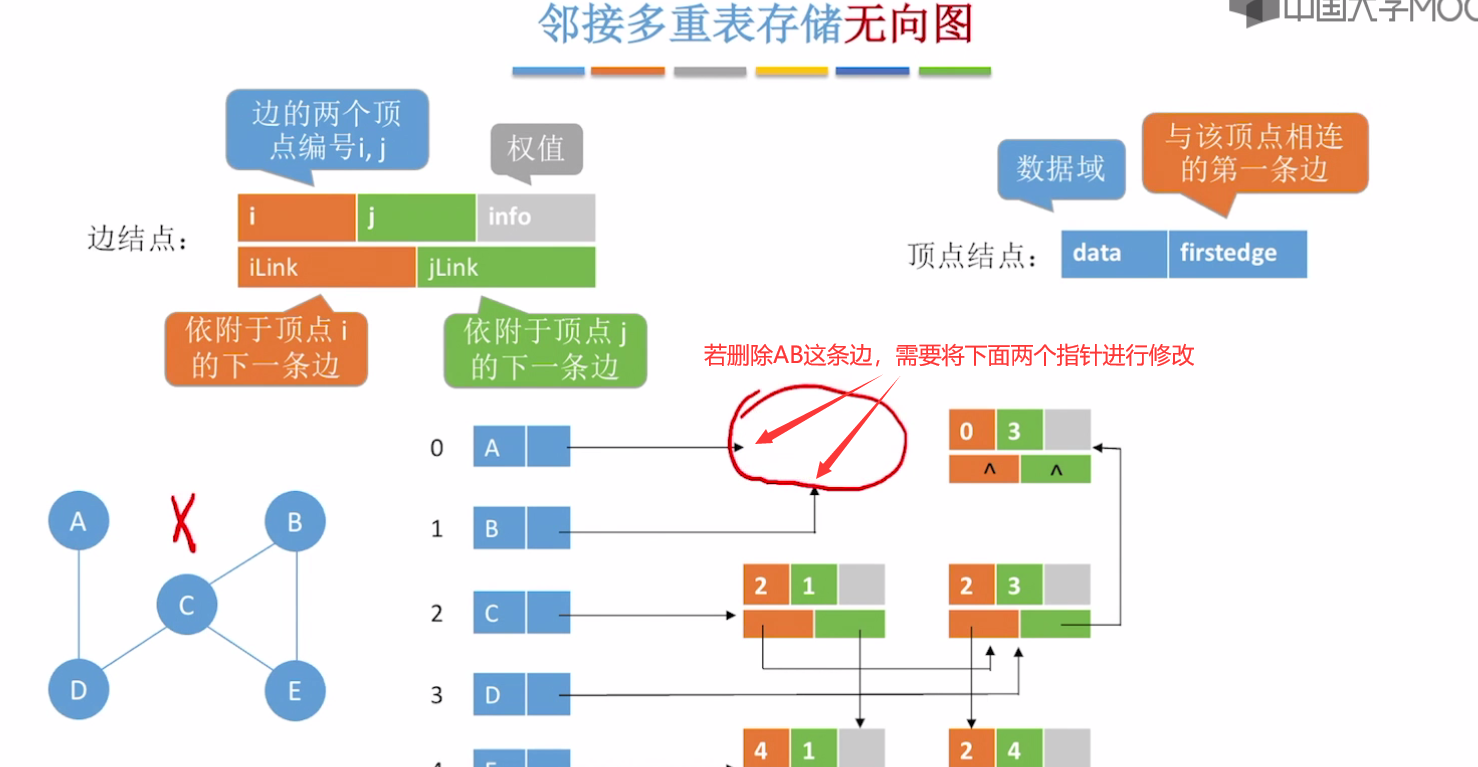
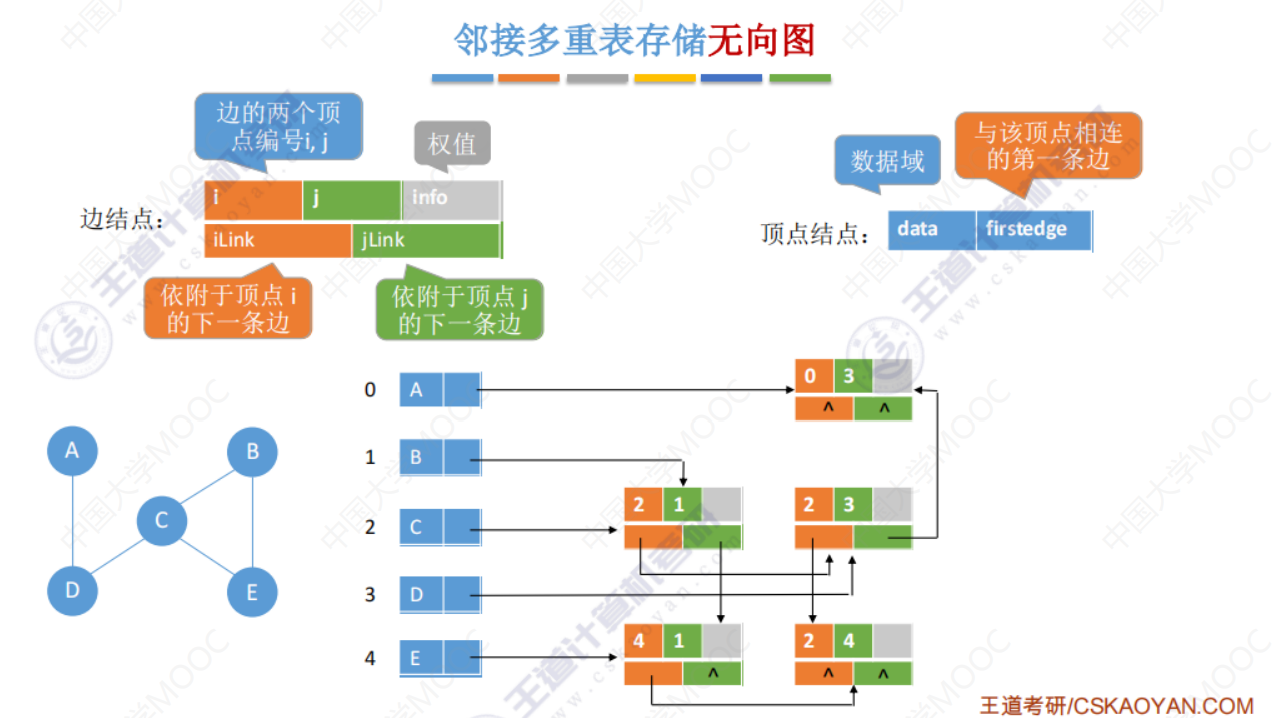
    在这里插入图片描述
    在这里插入图片描述

    删除一个顶点（同时也把与该顶点连接的边进行删除）

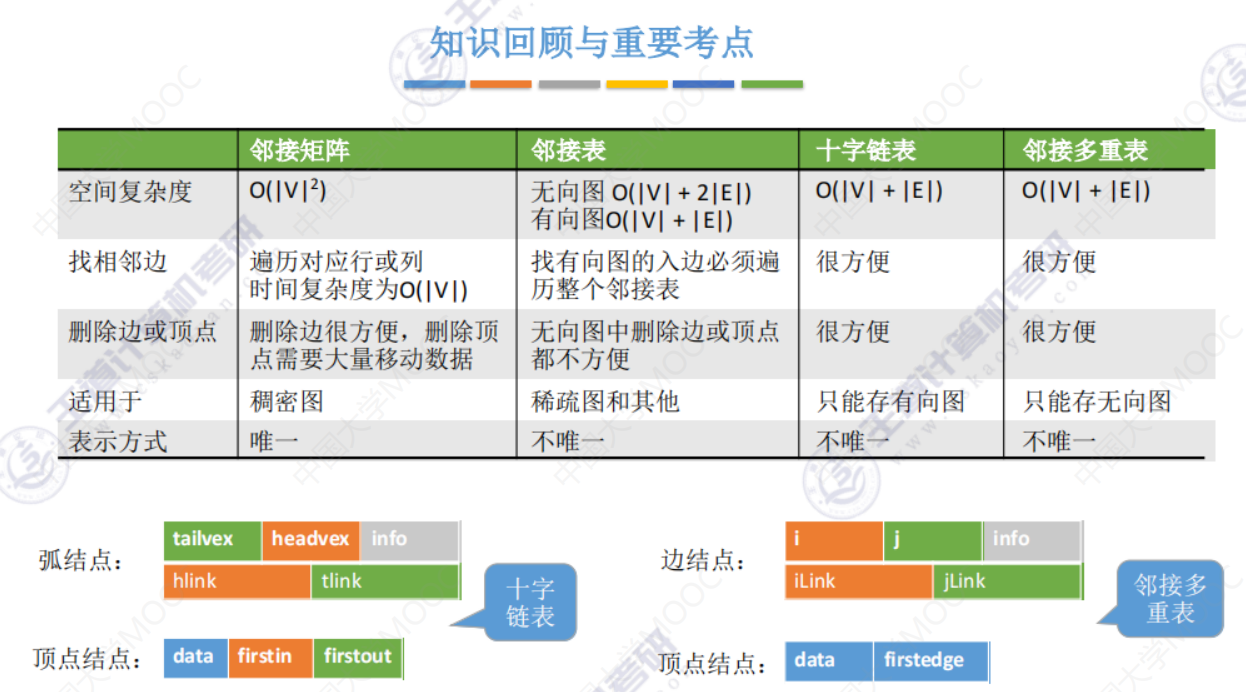
    在这里插入图片描述
    在这里插入图片描述

    邻接矩阵、邻接表、十字链表、邻接多重表 总结

    在这里插入图片描述

    6.2-4 图的基本操作

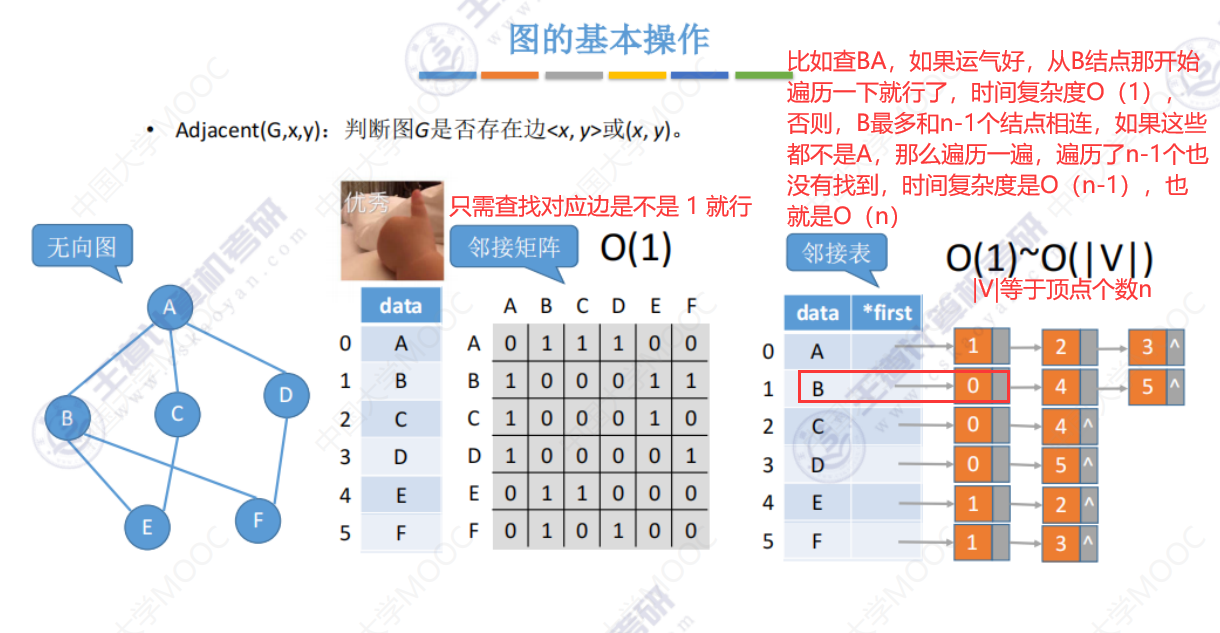
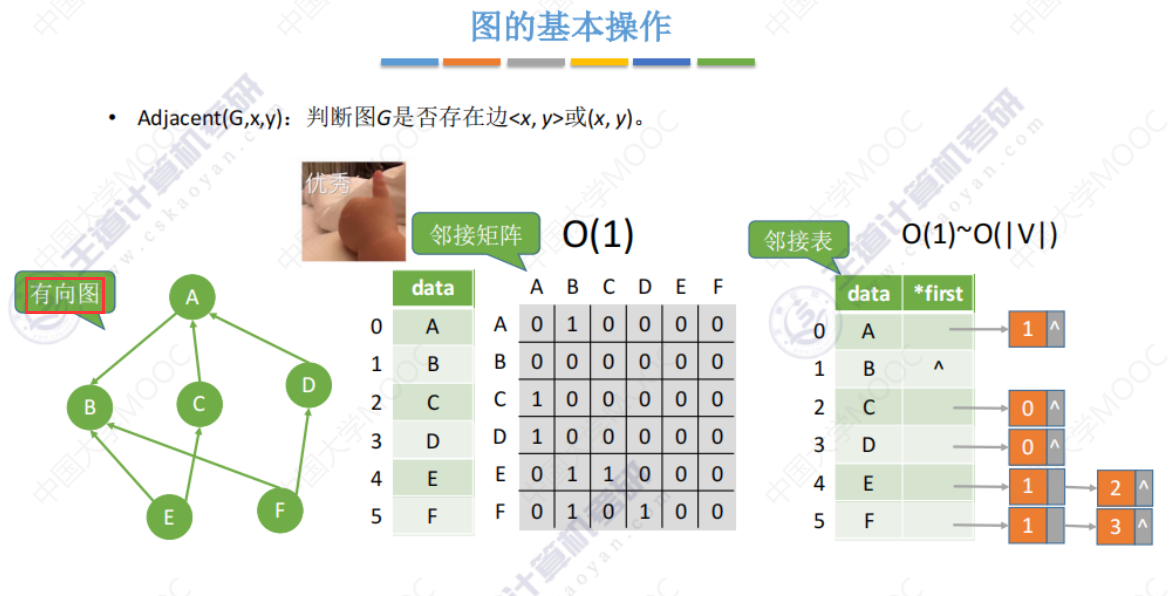
    在这里插入图片描述

    Adjacent（）

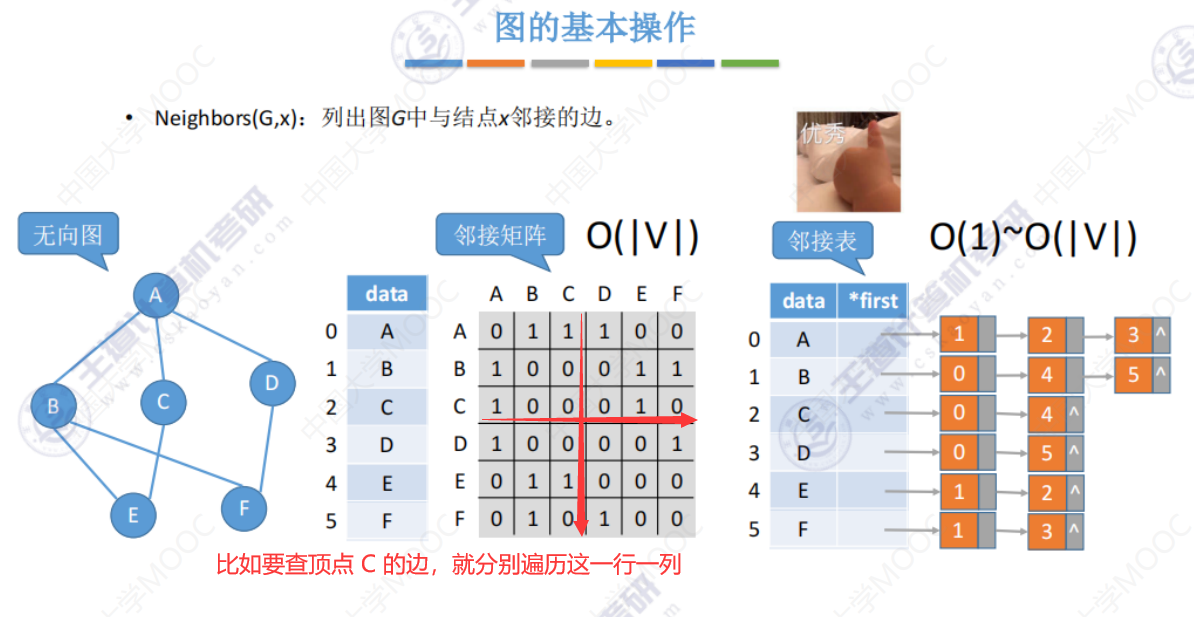
    在这里插入图片描述
    在这里插入图片描述

    Neighbors()

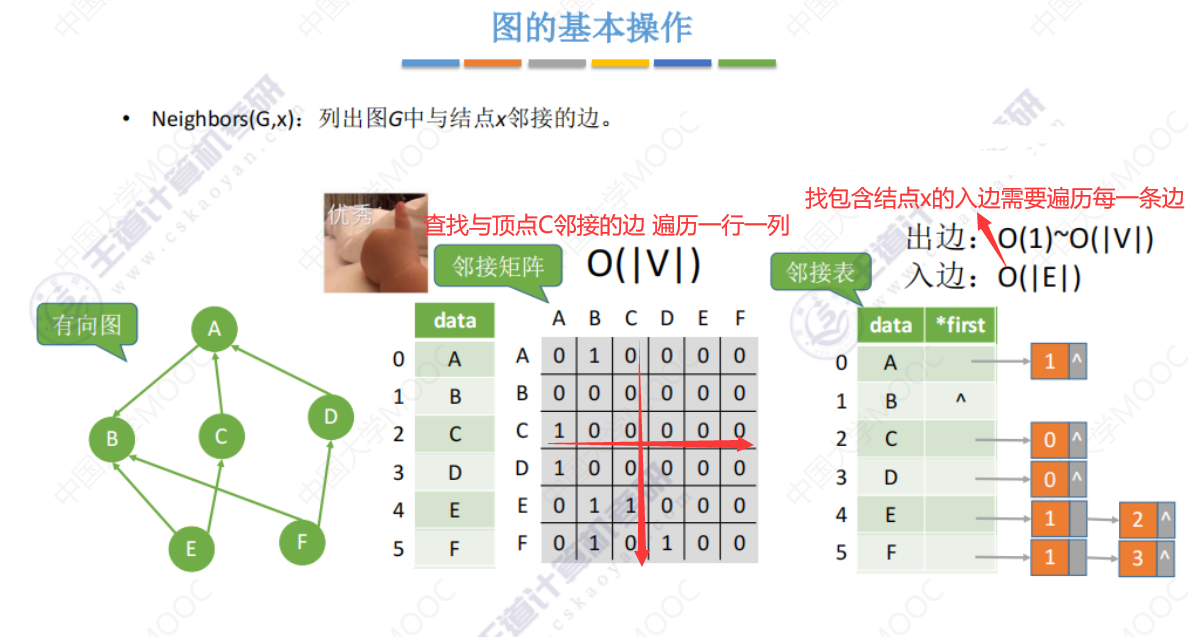
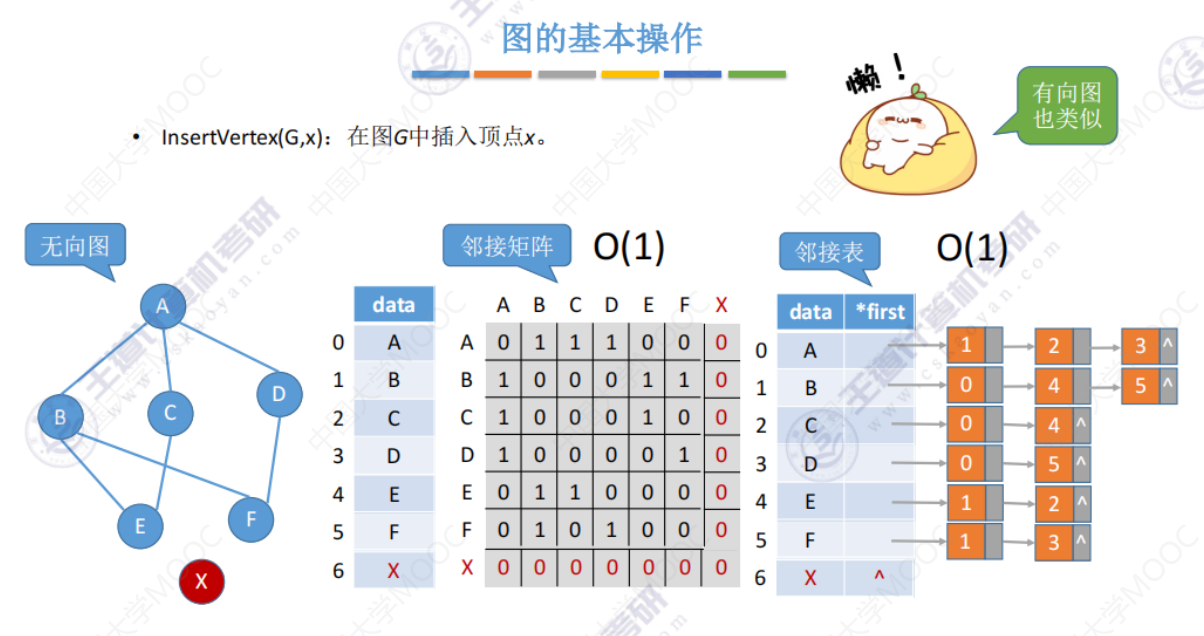
    在这里插入图片描述
    在这里插入图片描述

    InsertVertex()

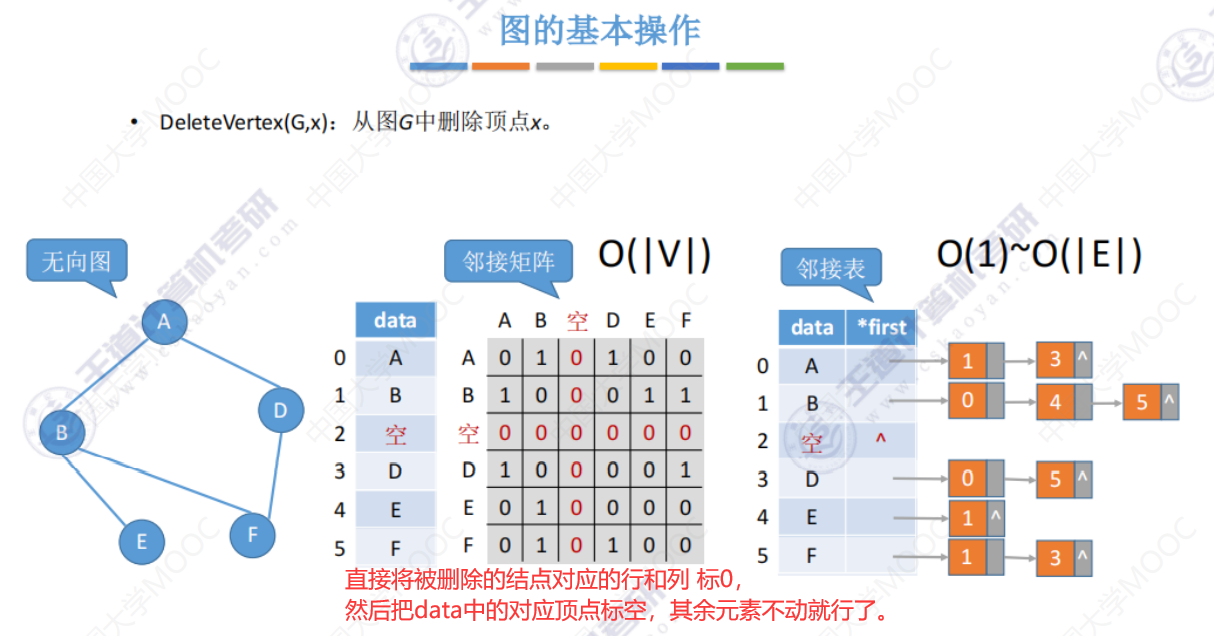
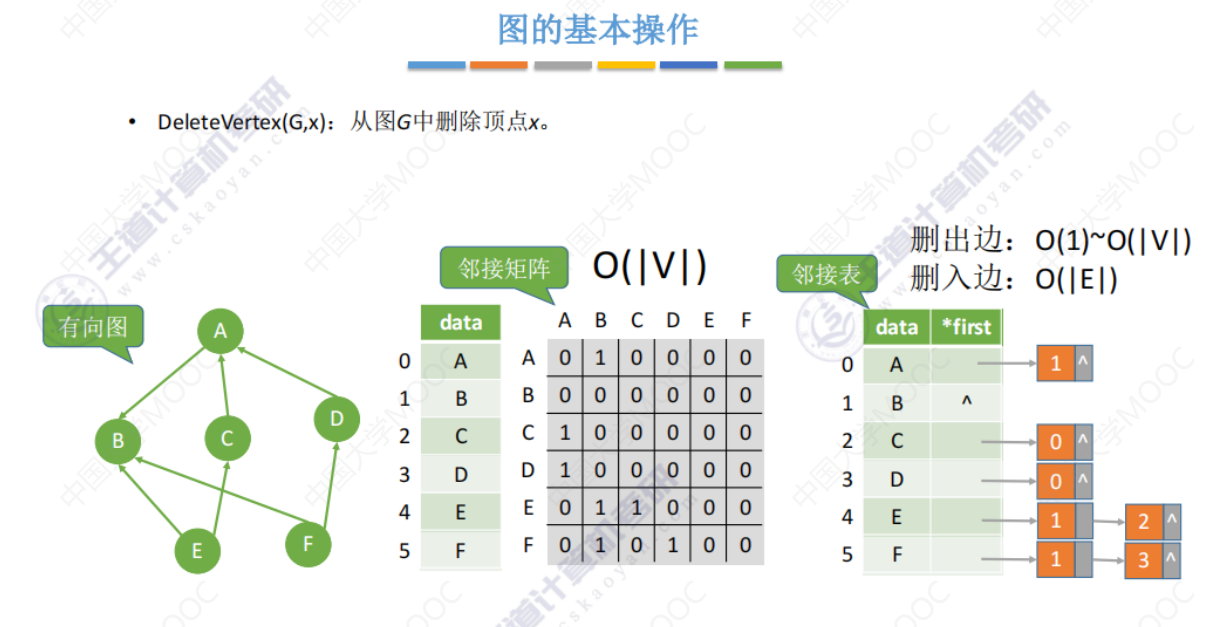
    在这里插入图片描述

    DeleteVertex()

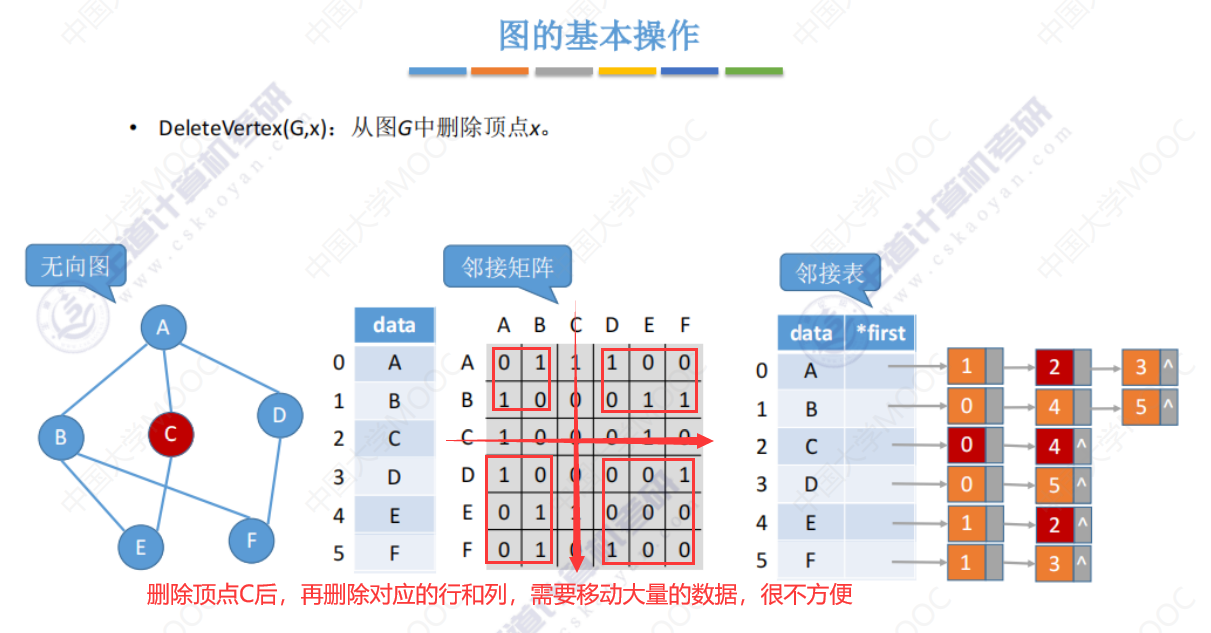
    在这里插入图片描述
    下图O(|E|)是 要遍历每一条边 来删除与 被删除结点 有关的边，如图中就是遍历每条边来删除与结点C有关的边。
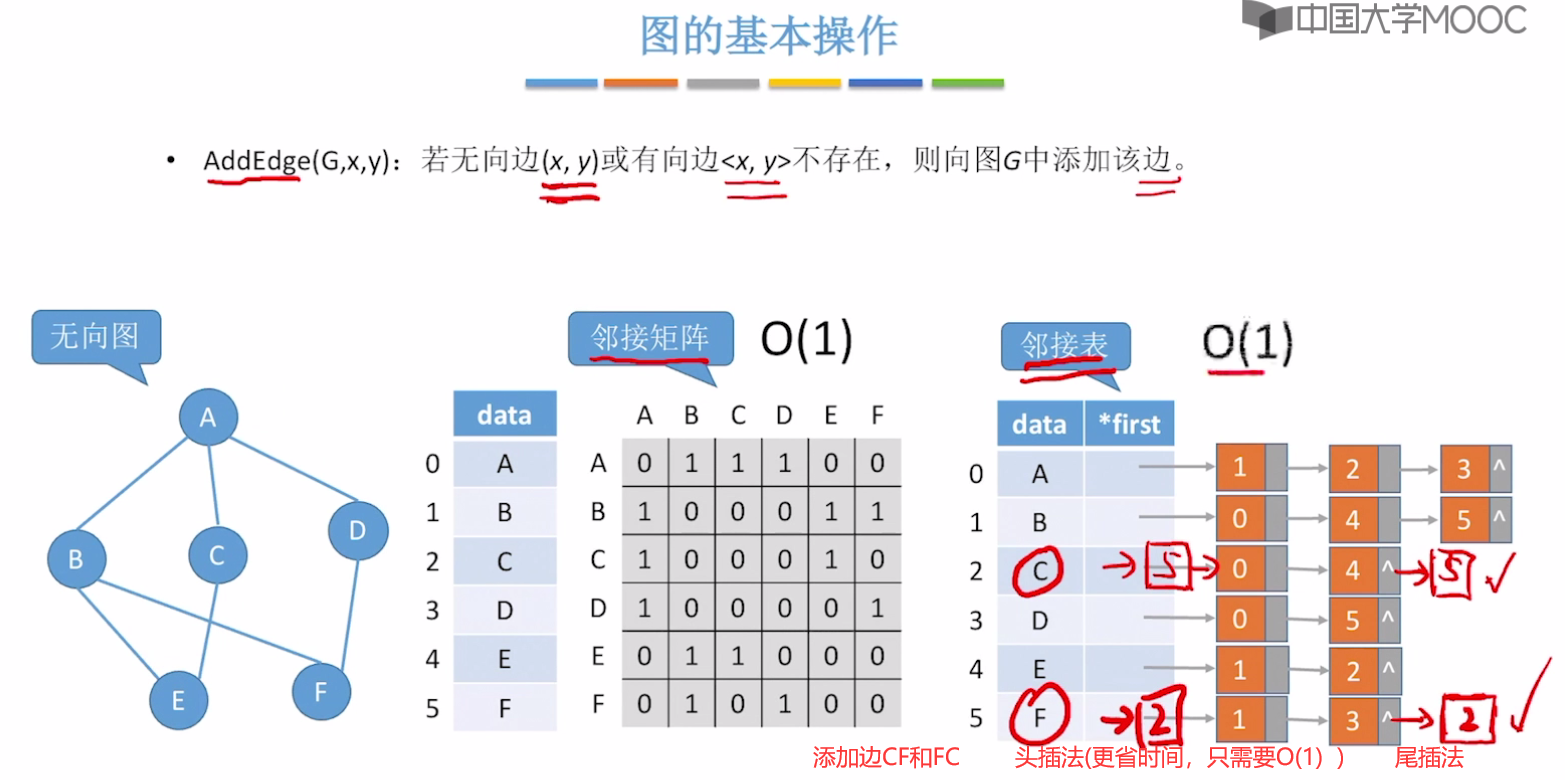
    在这里插入图片描述
    在这里插入图片描述

    AddEdge（）

    在这里插入图片描述

    RemoveEdge()

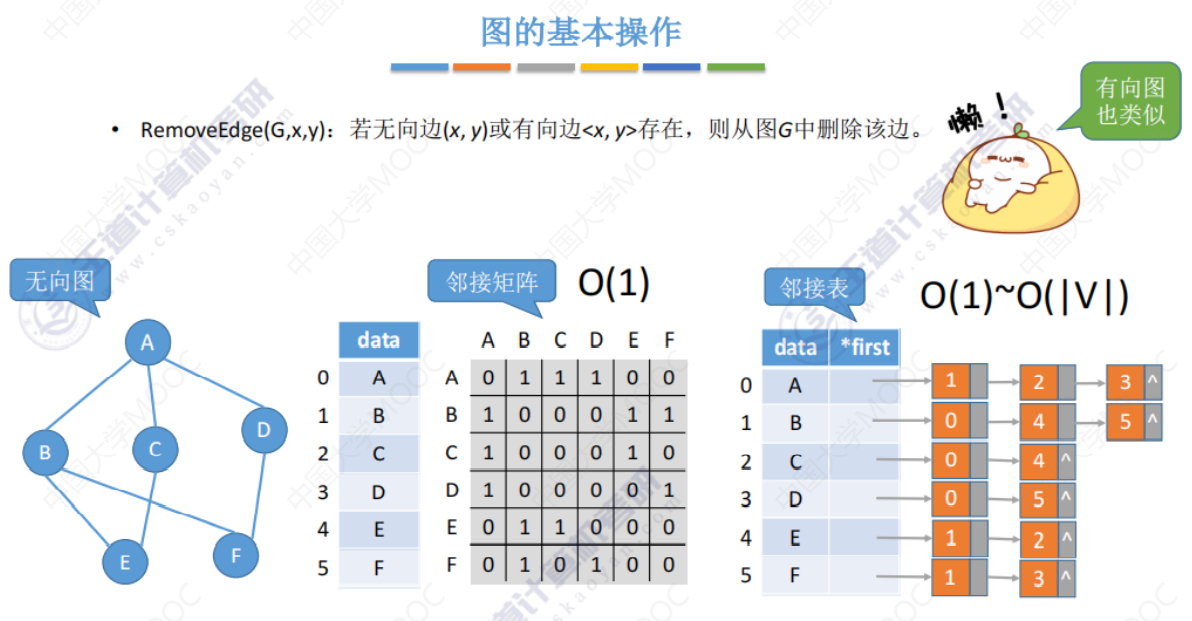
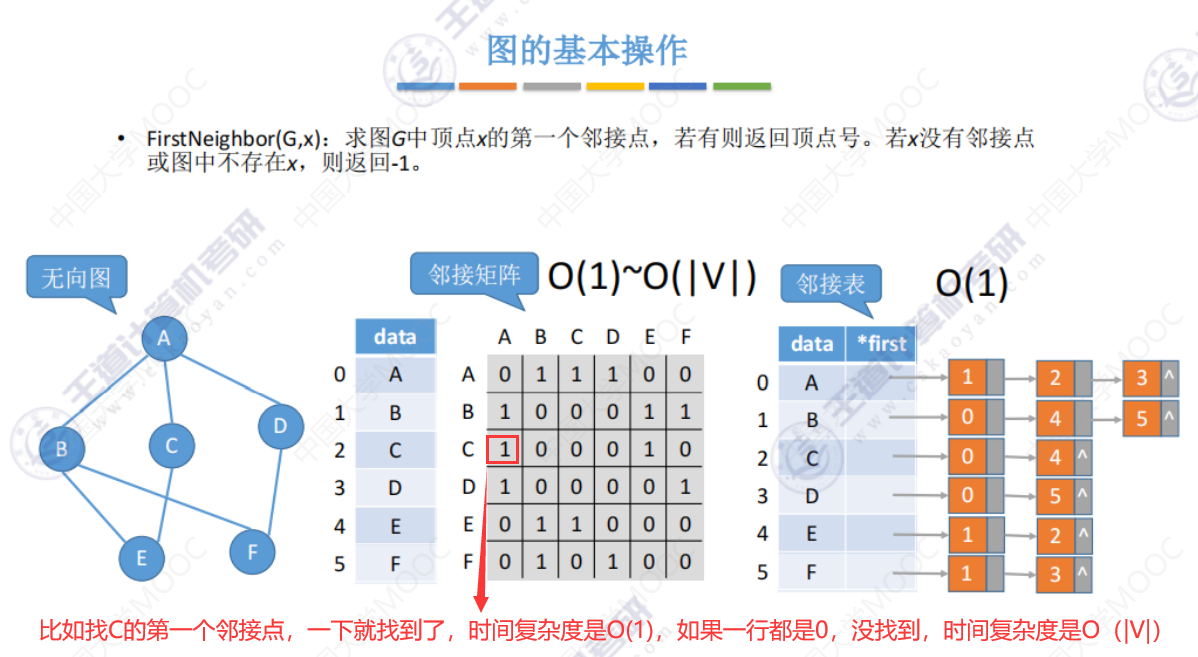
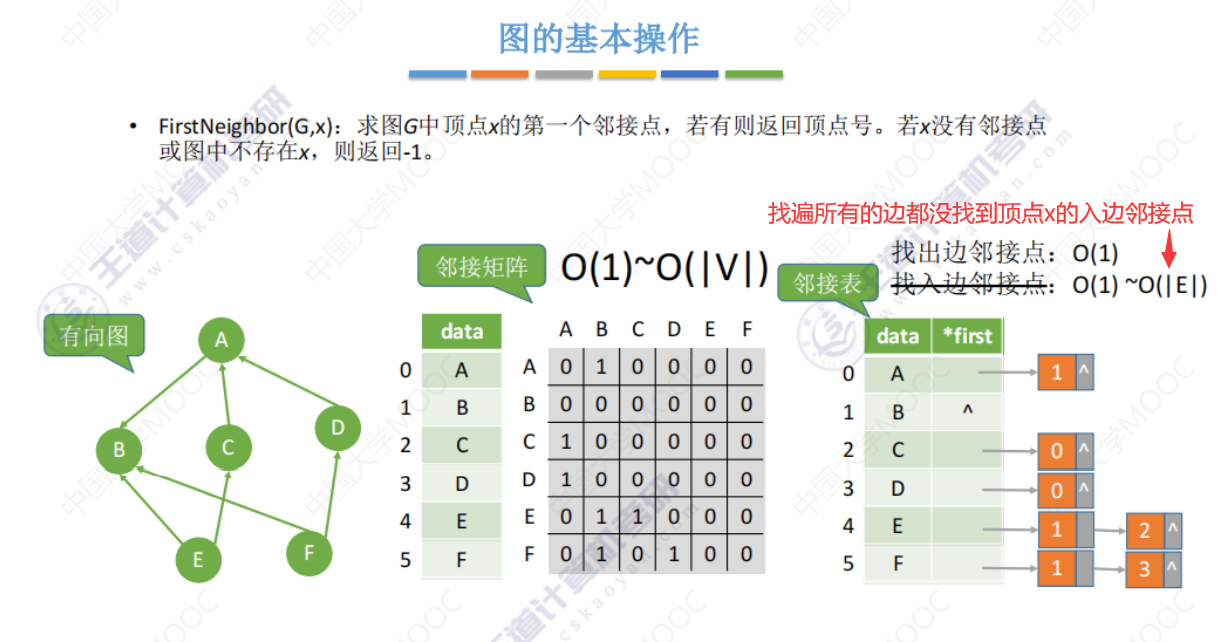
    在这里插入图片描述

    FirstNeighbor()

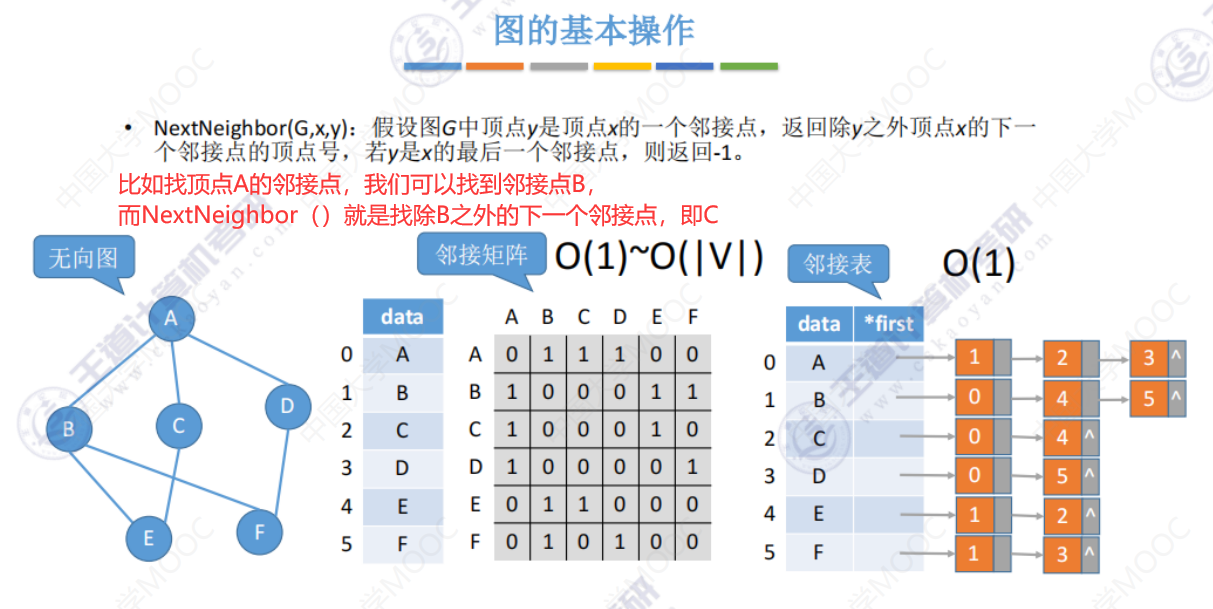
    在这里插入图片描述
    在这里插入图片描述

    NextNeighbor()

    在这里插入图片描述

    获取或设置权值

    获取或设置权值 即 找到对应的边，然后获取或设置权值（获取和设置权值的时间复杂度是O(1) ）。所以获取或设置权值的整体操作（包括找边和设置权值）和 只找边的时间复杂度相同。
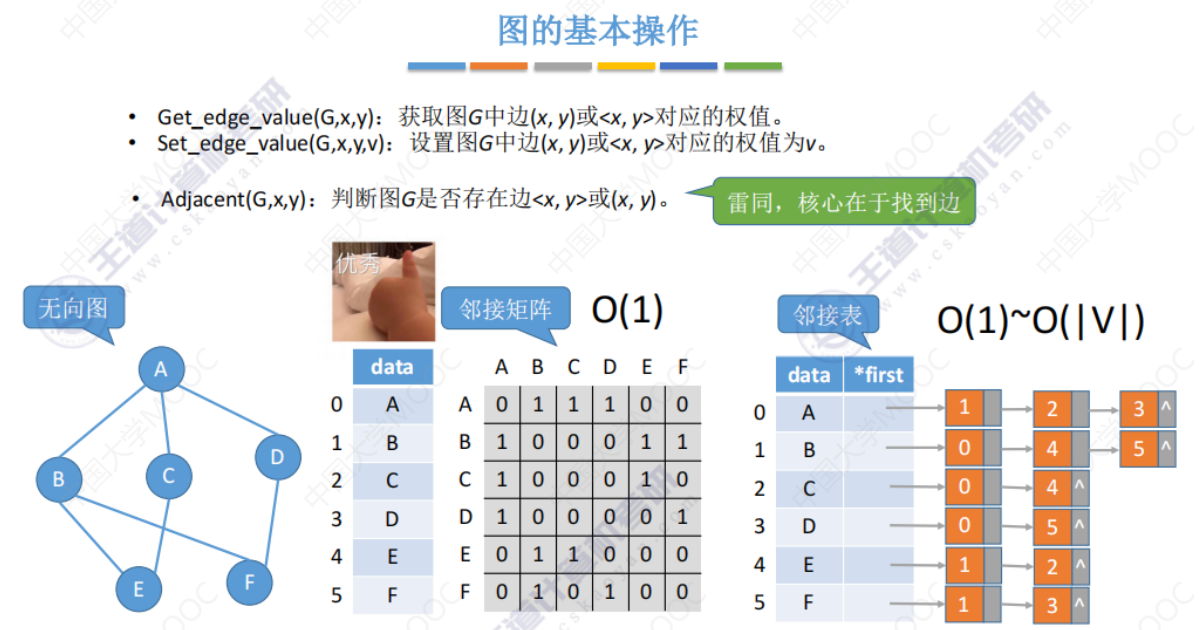
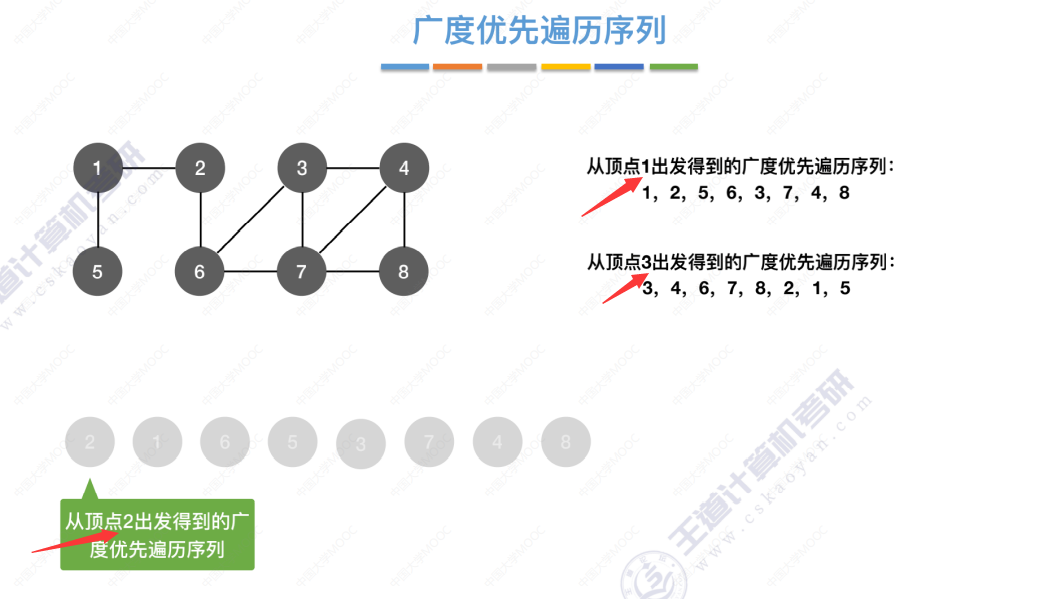
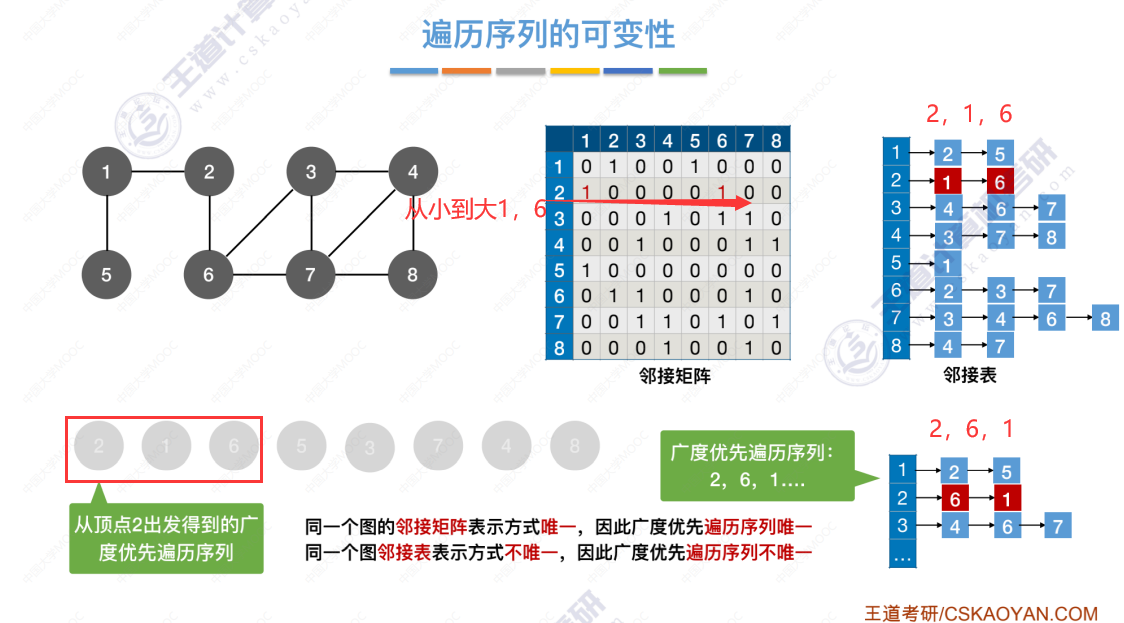
    在这里插入图片描述

    6.3-1 图的广度优先遍历

    广度优先遍历代码引入

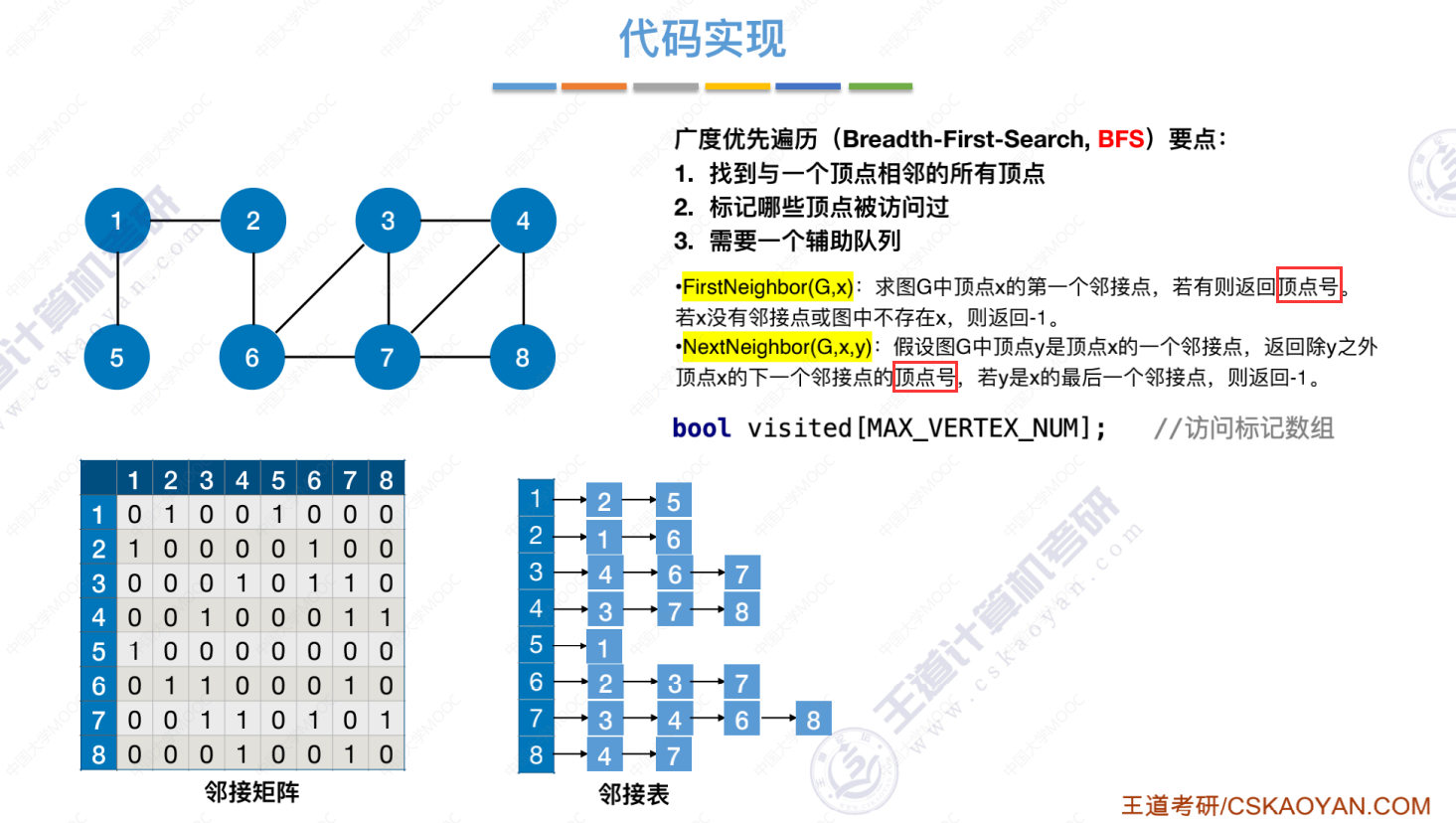
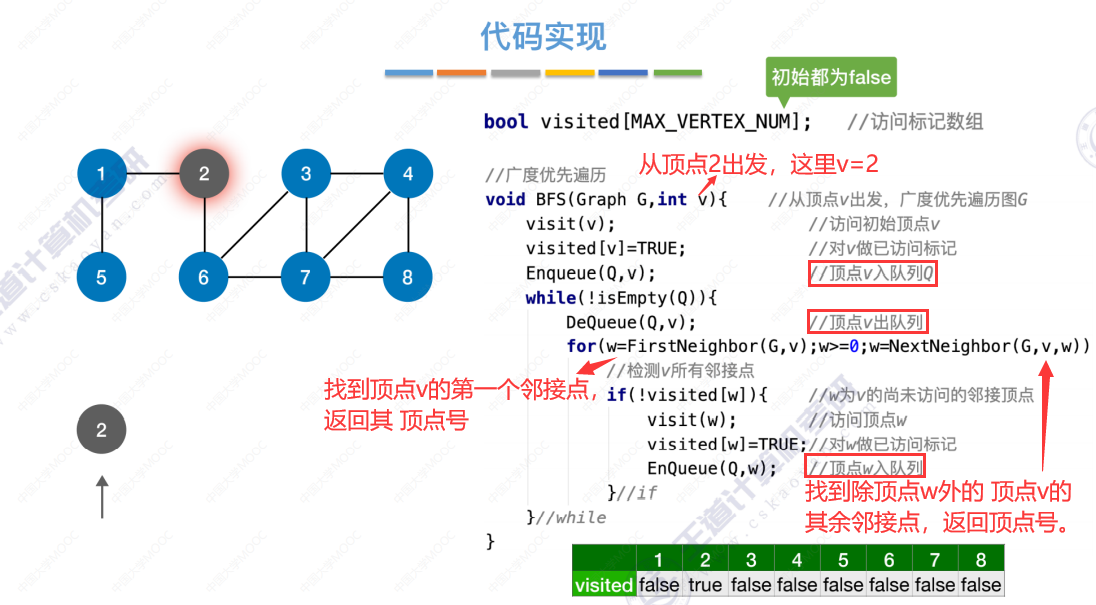
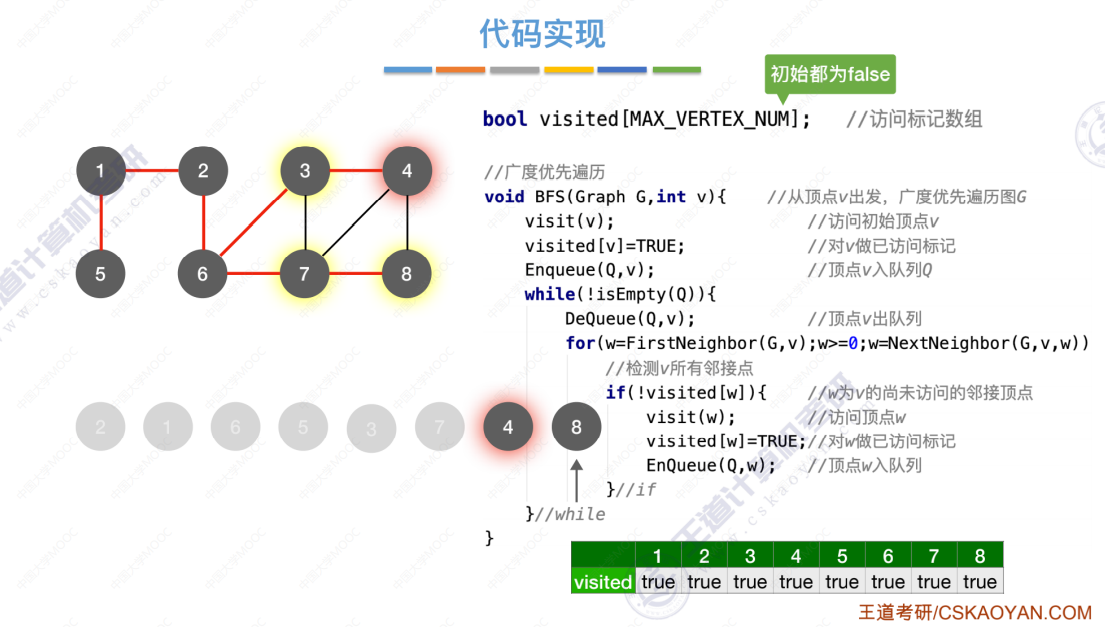
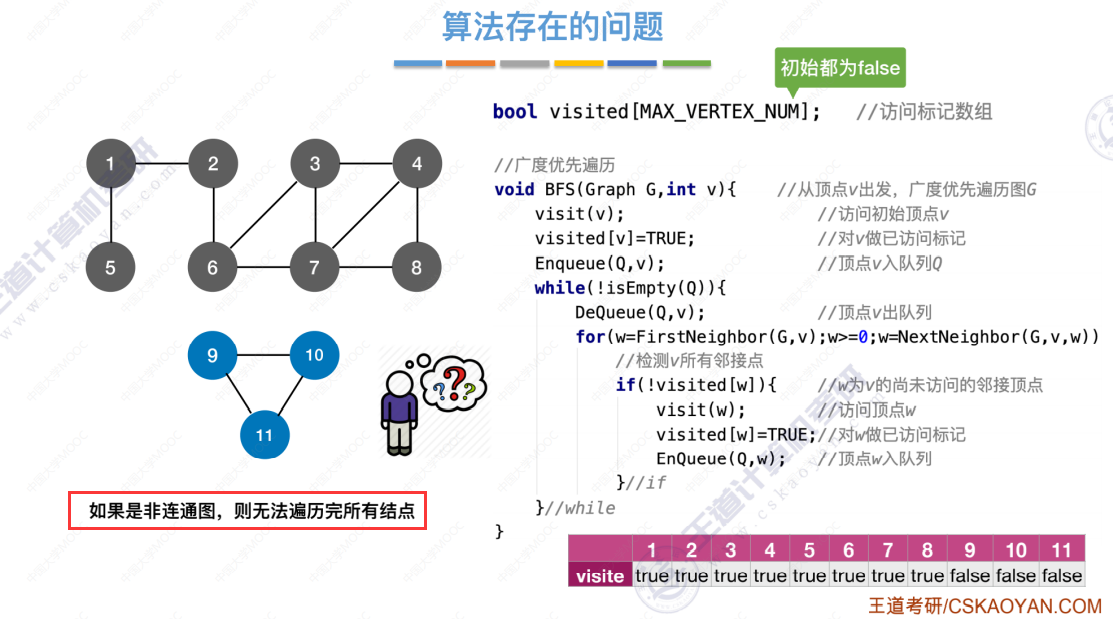
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述

    算法存在的问题

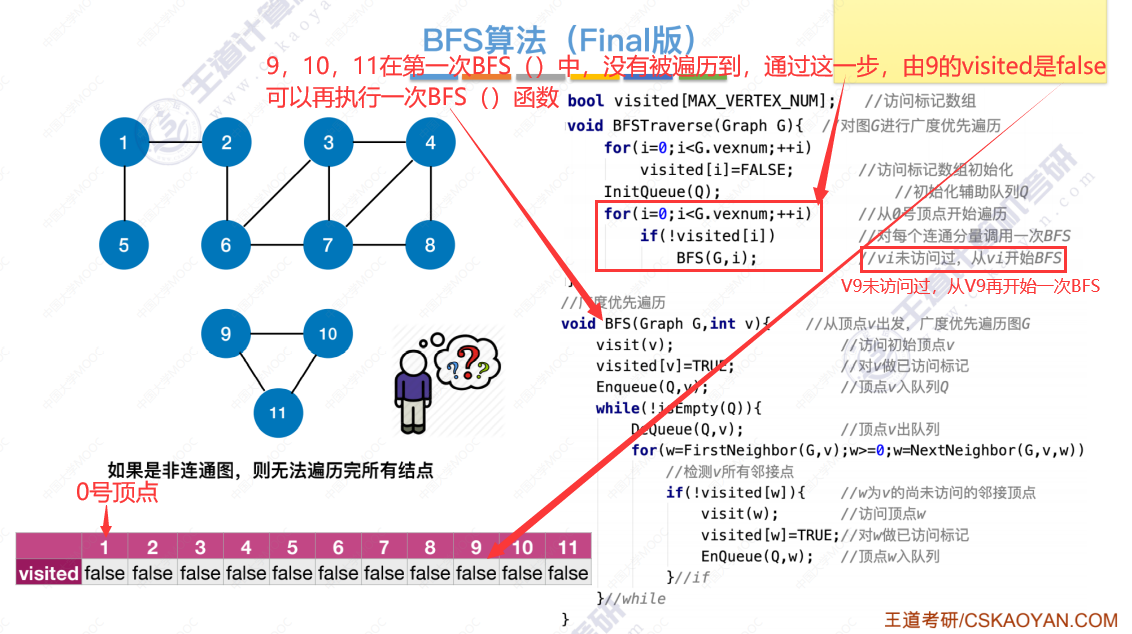
    在这里插入图片描述

    广度优先算法（Breadth-First-Search，BFS算法）最终版

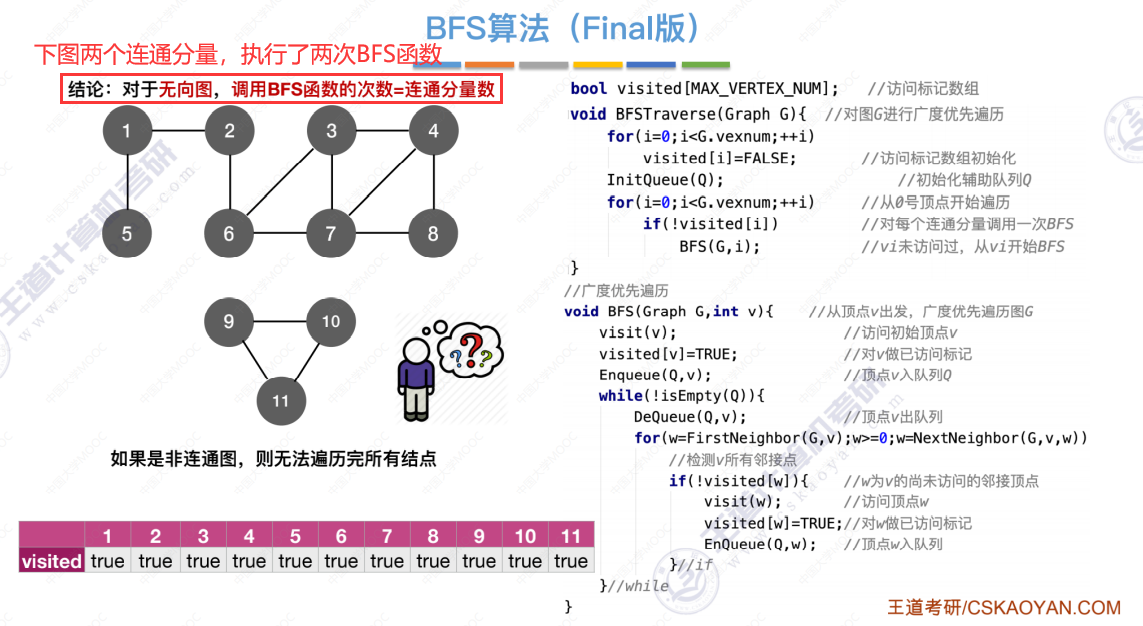
    在这里插入图片描述
    在这里插入图片描述

    算法分析

    空间复杂度

    最坏情况，要一次把所有邻接点（即其余结点装入辅助队列），此时空间复杂度最高。
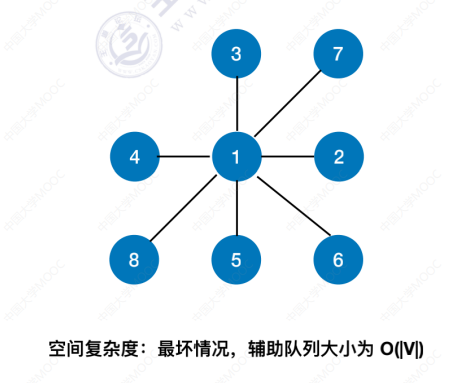
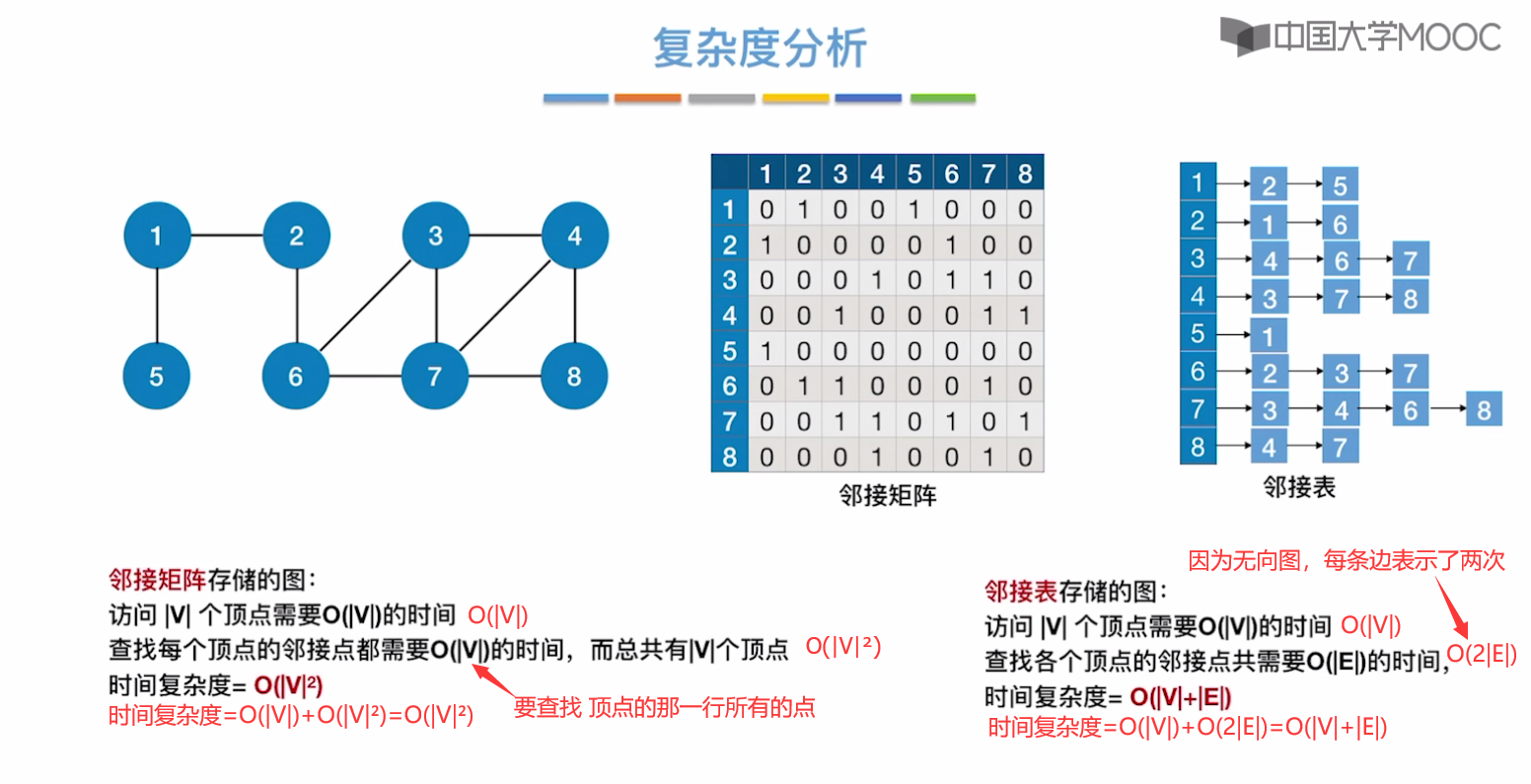
    在这里插入图片描述

    时间复杂度

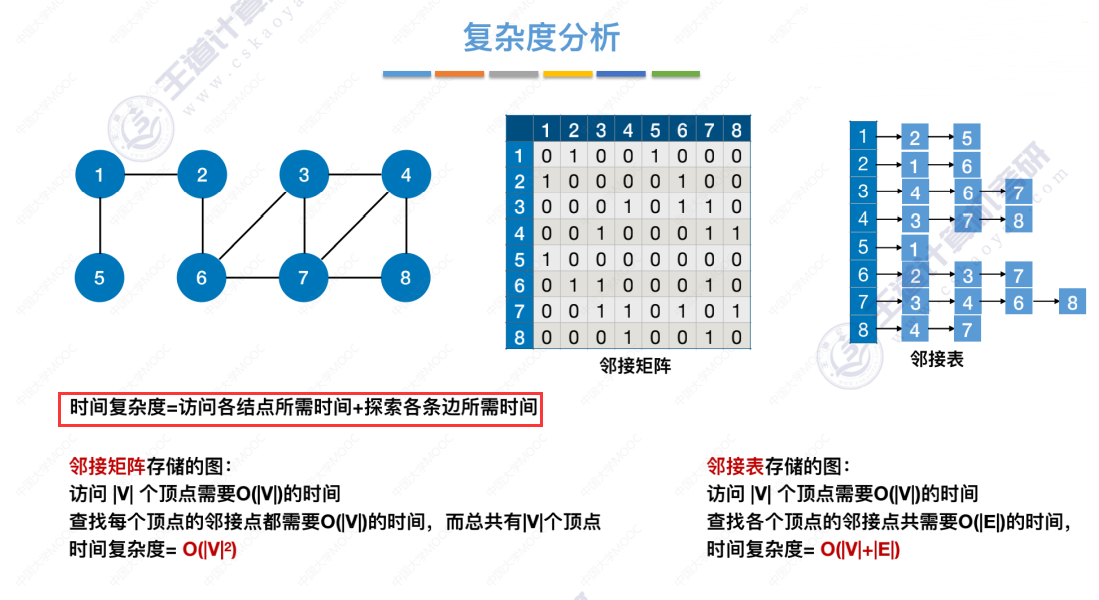
    算法时间开销主要是：访问各个顶点和查找每个顶点的邻接点。
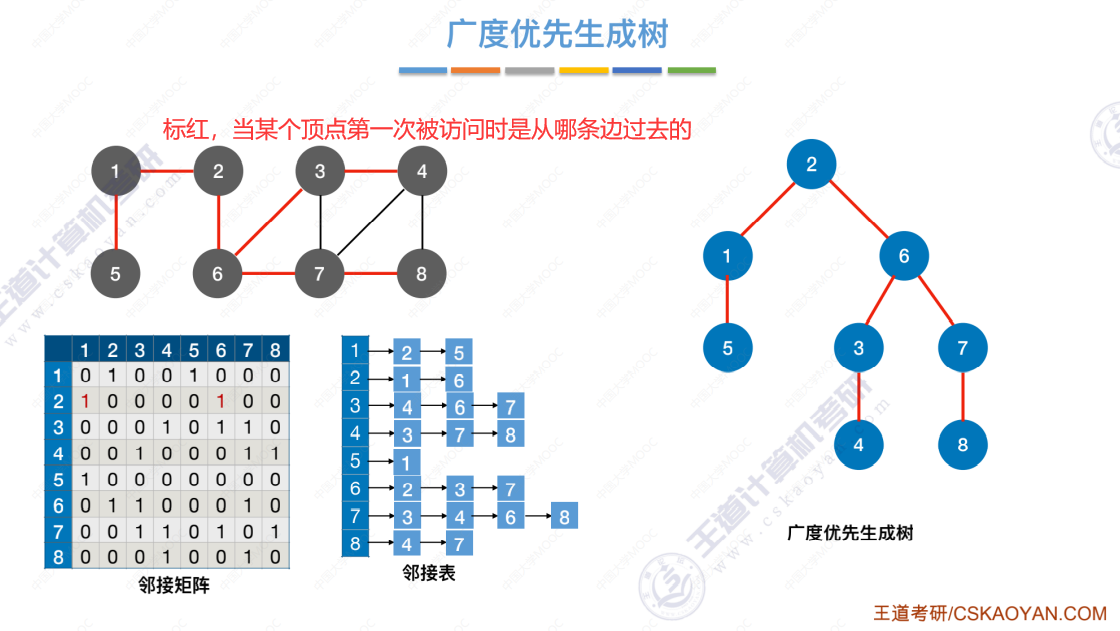
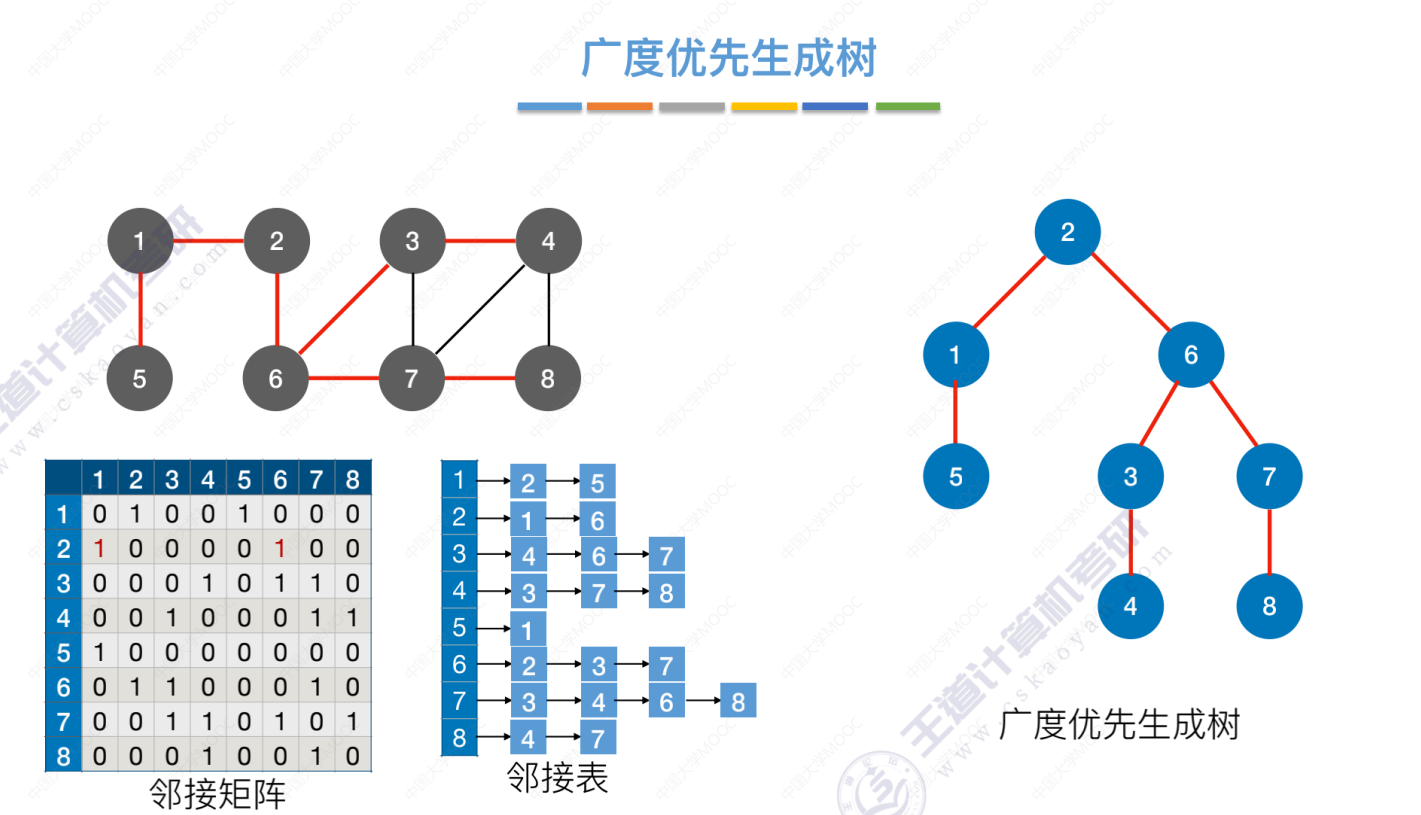
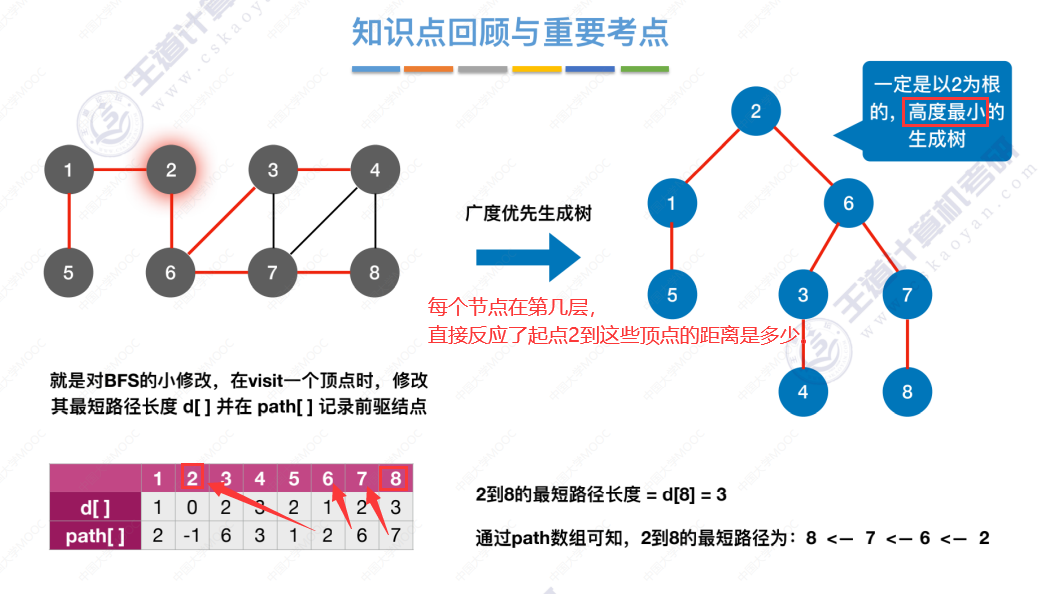
    在这里插入图片描述

    广度优先生成树

    标红，当某个顶点第一次被访问时是从哪条边过去的
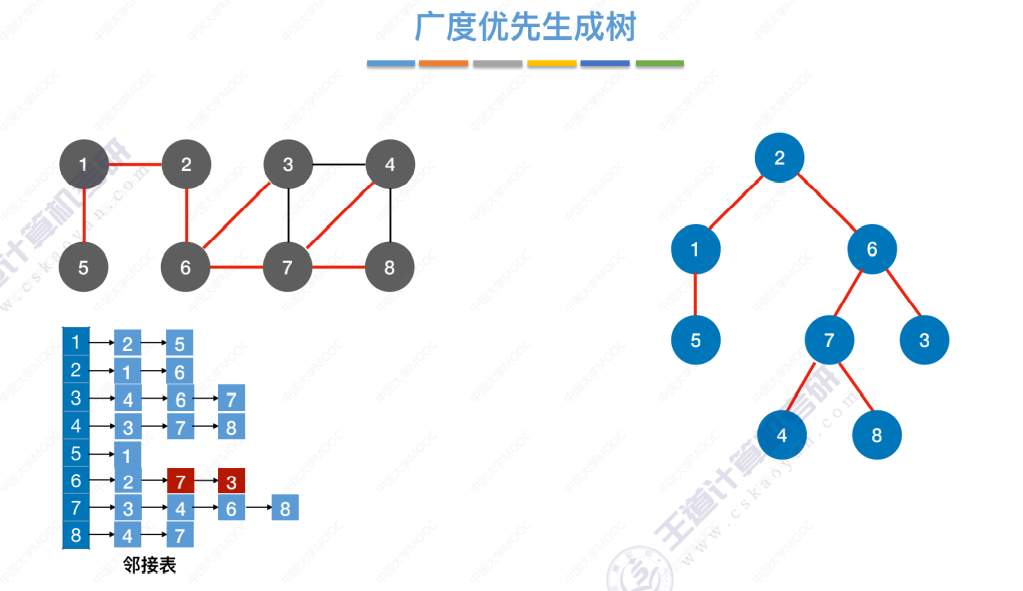
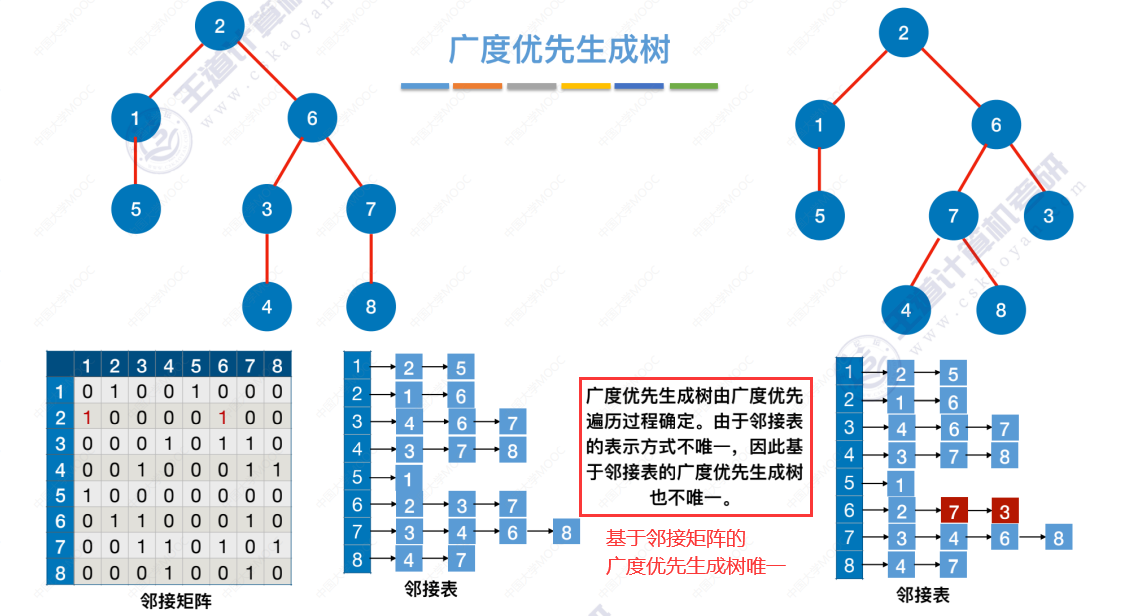
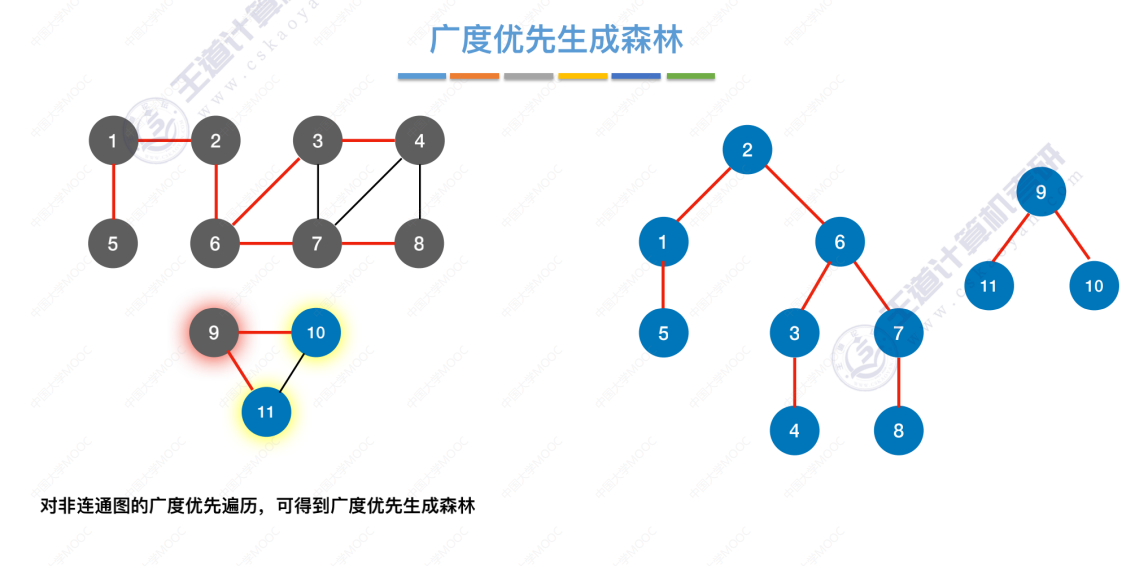
    在这里插入图片描述在这里插入图片描述
    在这里插入图片描述

    广度优先生成森林

    把广度优先生成树放在一起，就是广度优先生成森林。
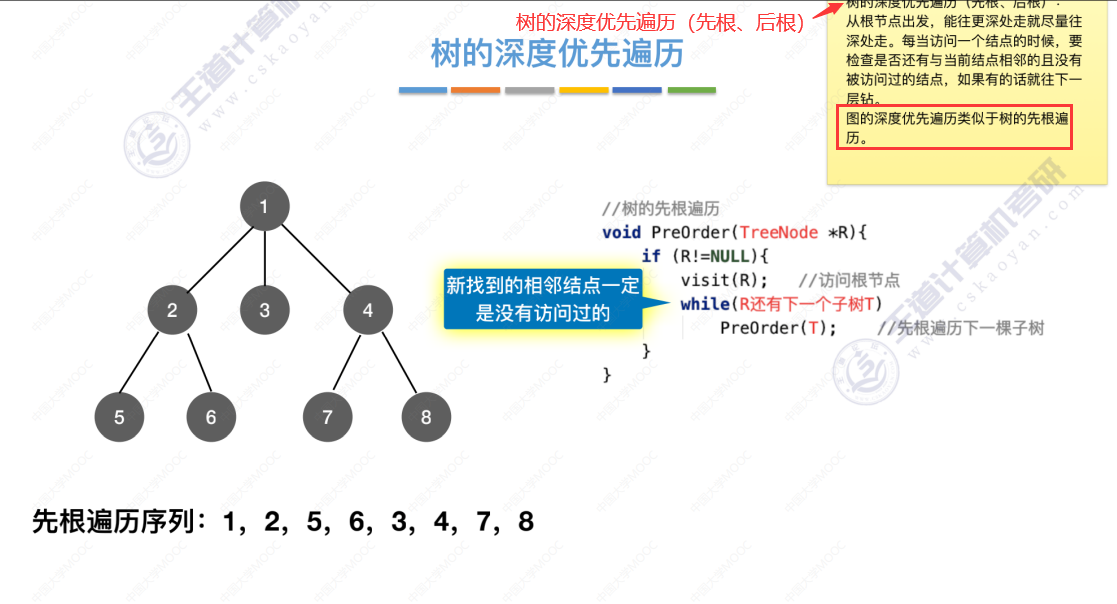
    在这里插入图片描述

    6.3-2 图的深度优先遍历

    图的深度优先遍历类似于树的先根遍历

    在这里插入图片描述

    图的深度优先遍历代码 引入

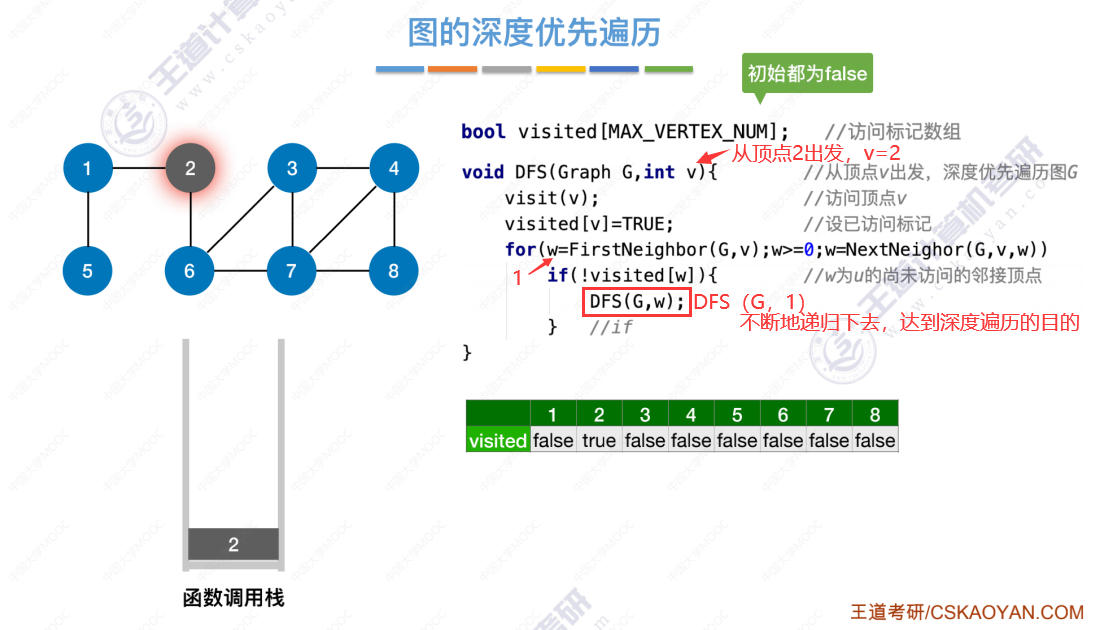
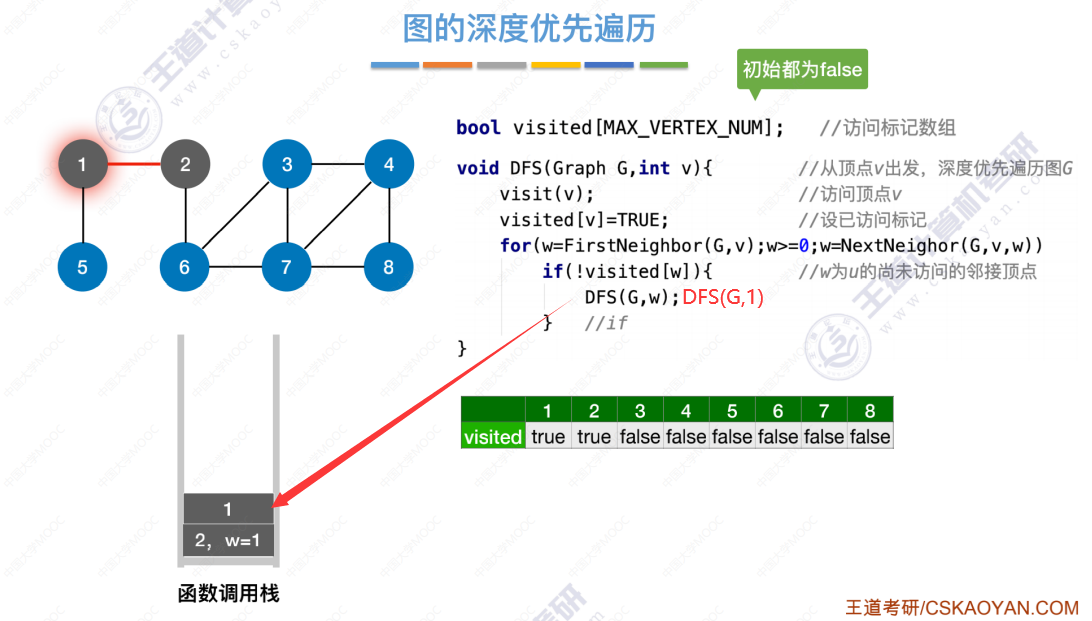
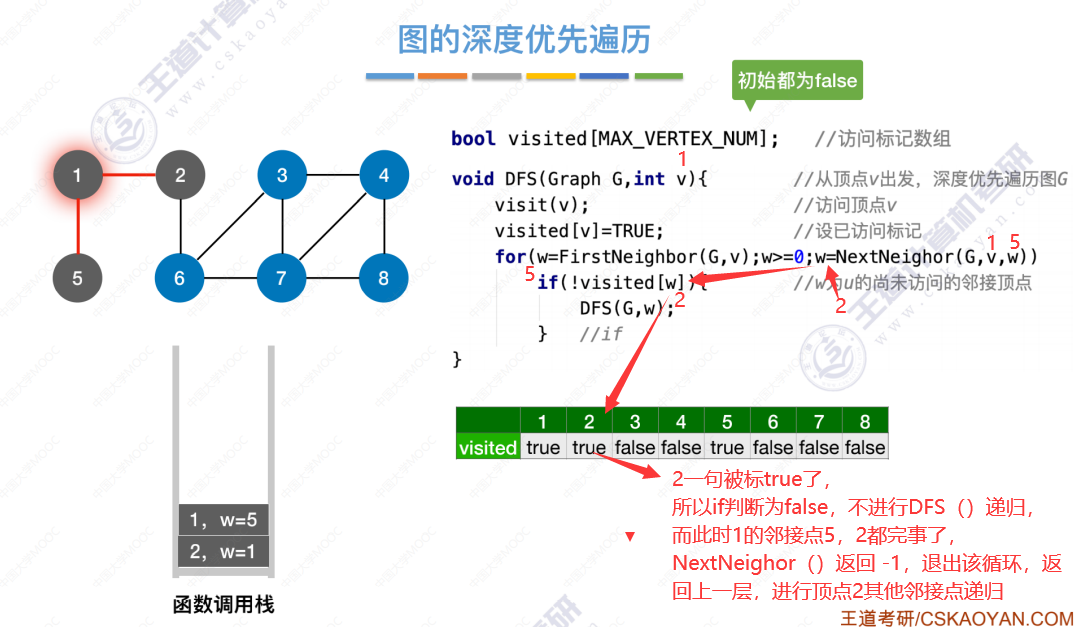
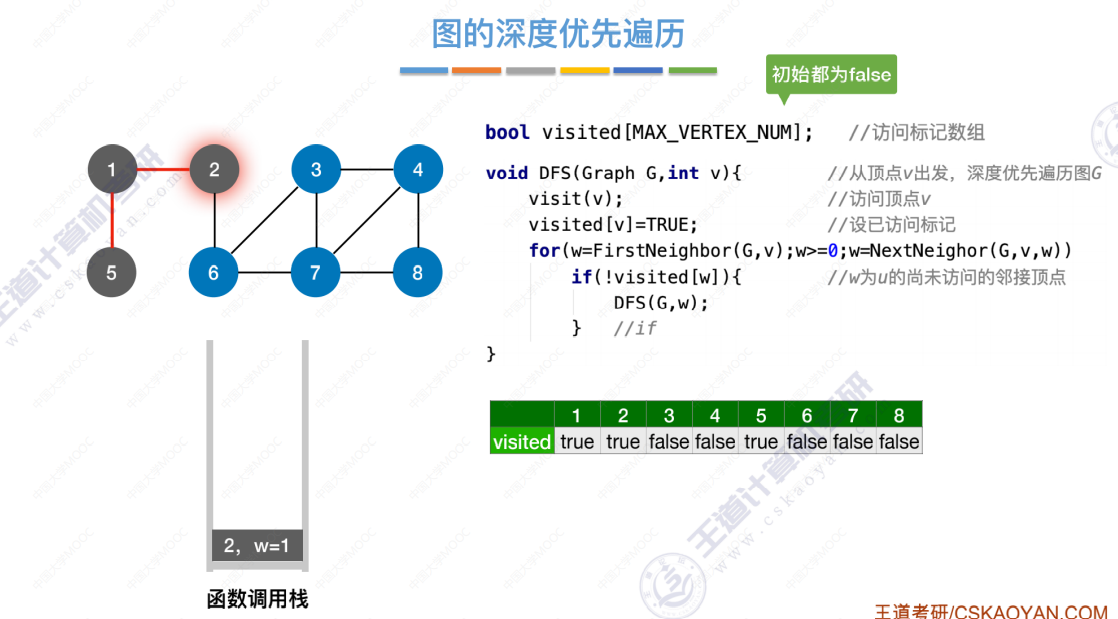
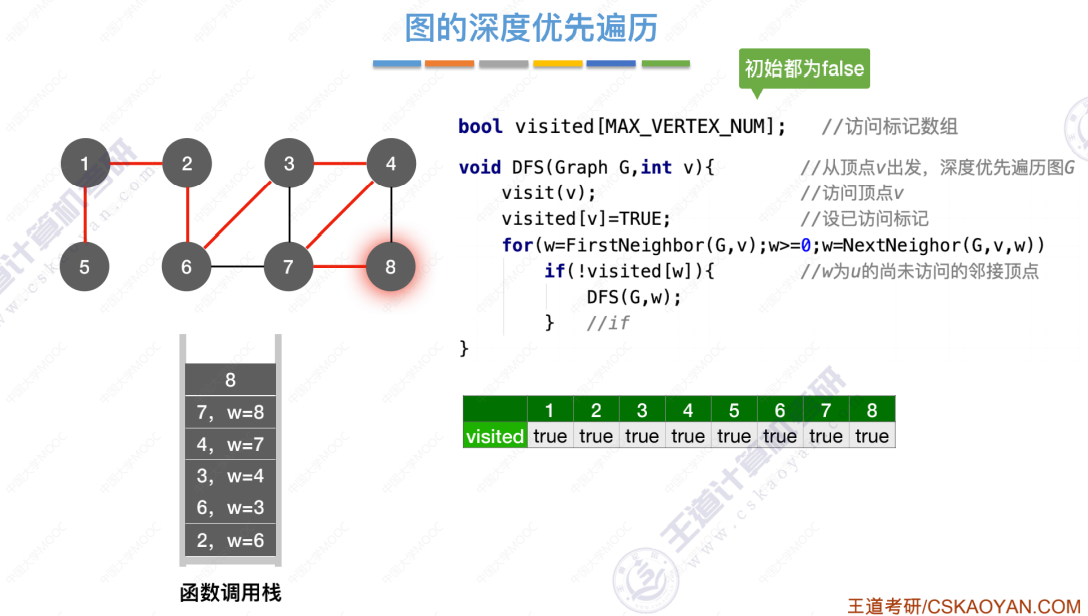
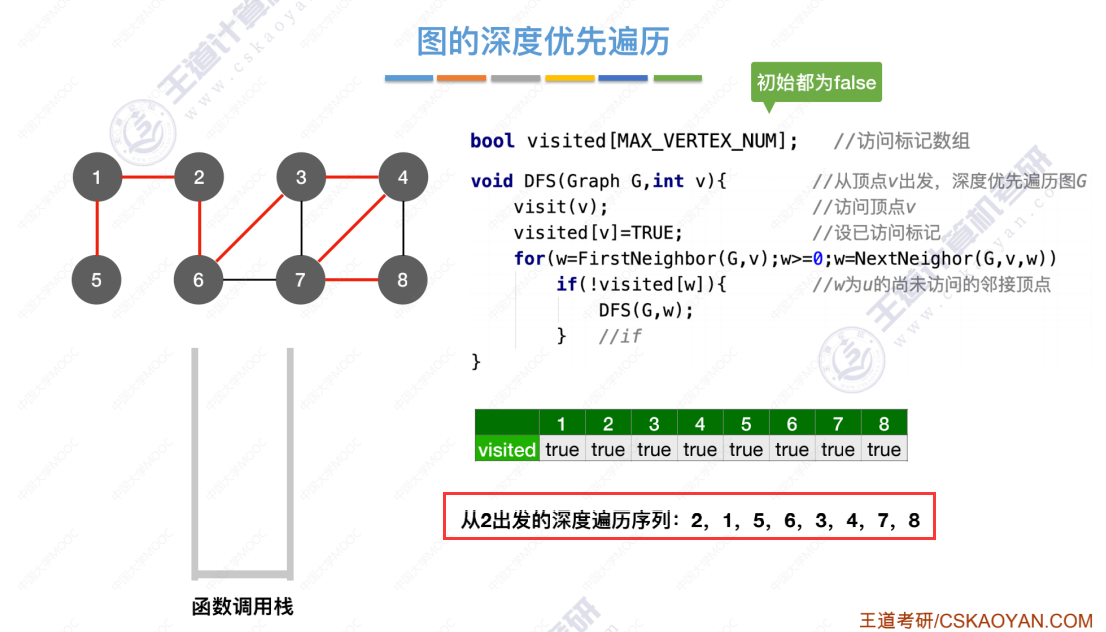
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述

    算法存在的问题（和广度优先存在的问题一样，无法处理非连通图，解决办法也一样）

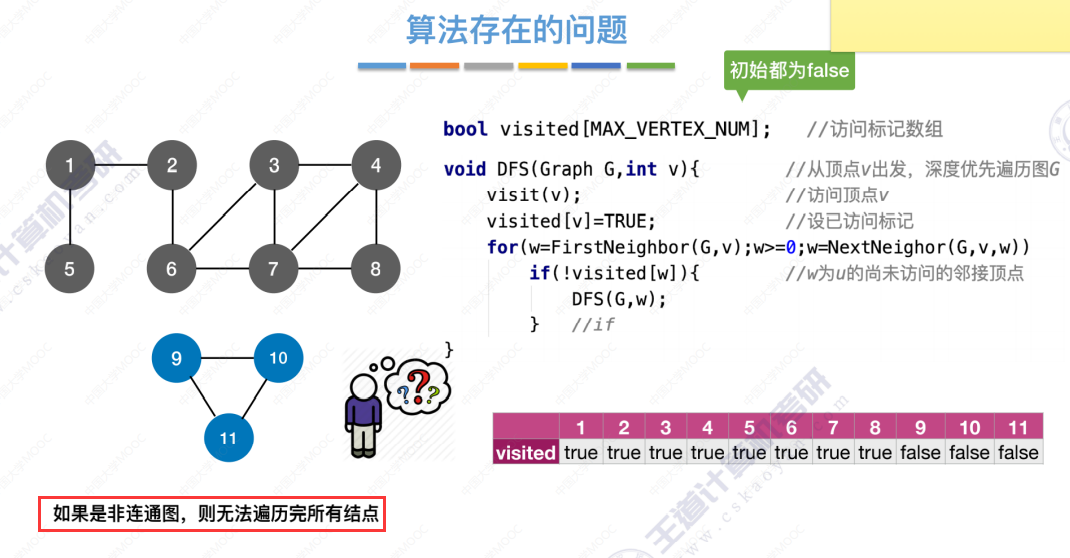
    在这里插入图片描述

    深度优先遍历算法（Depth-First-Search）最终版

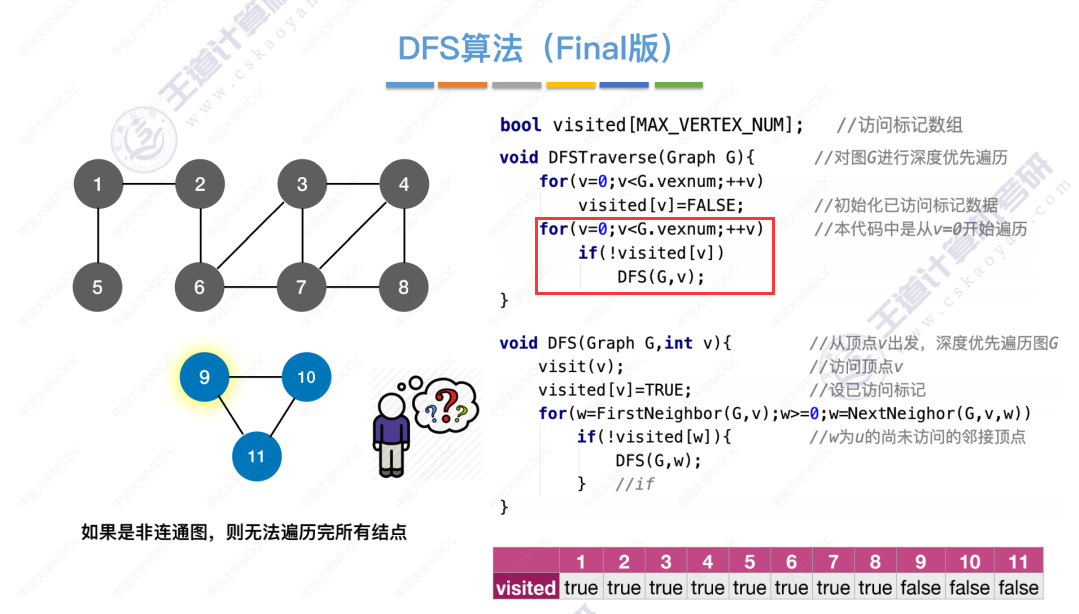
    在这里插入图片描述

    算法分析

    空间复杂度

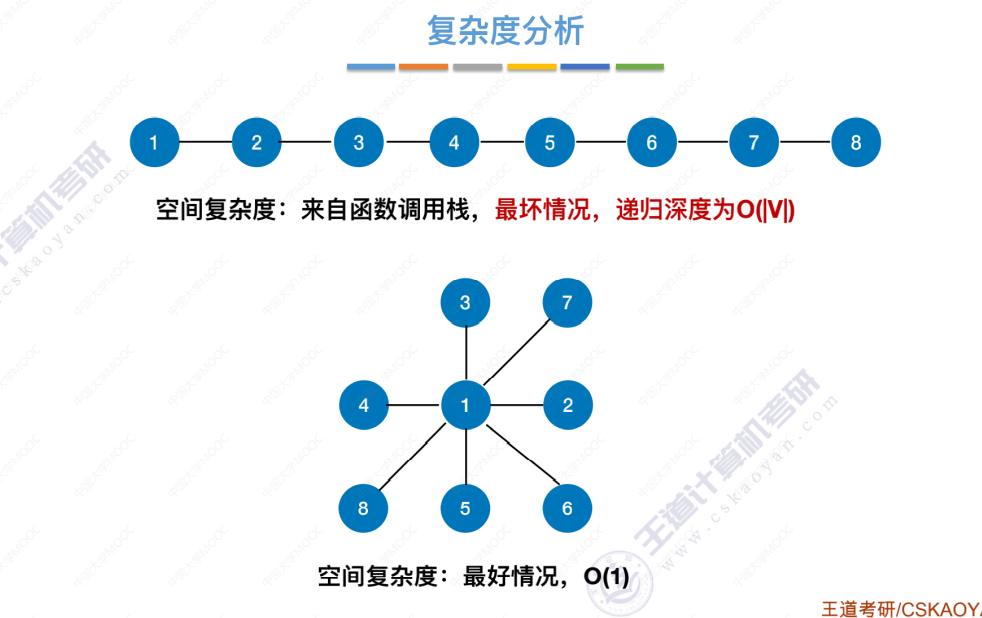
    在这里插入图片描述

    时间复杂度

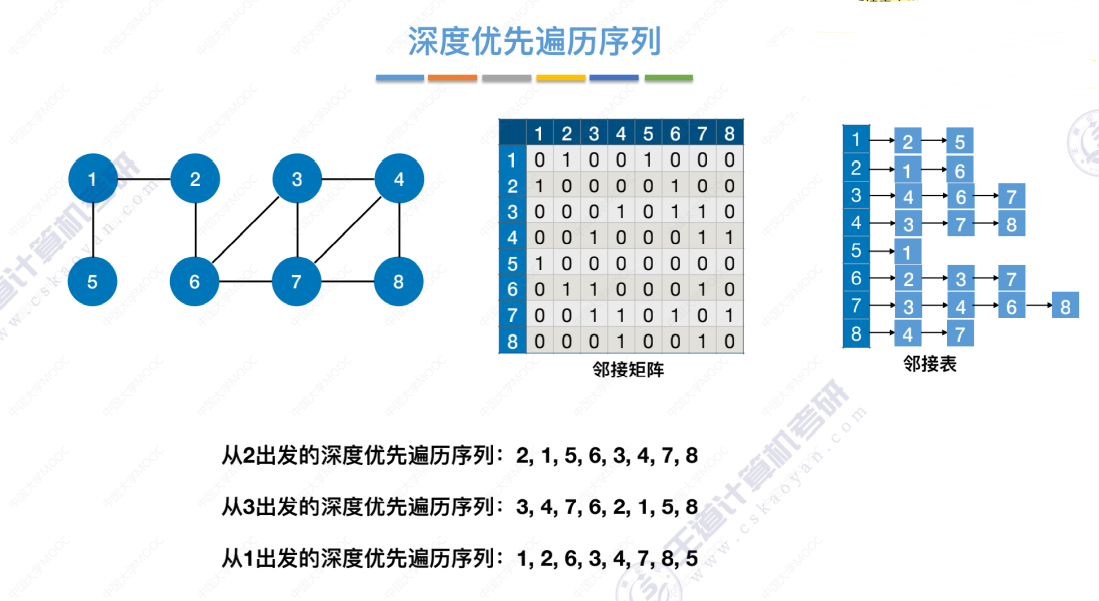
    在这里插入图片描述

    数据结构-图的源码
    tgz 4星 超过75%的资源 11KB
    下载

    深度优先遍历序列

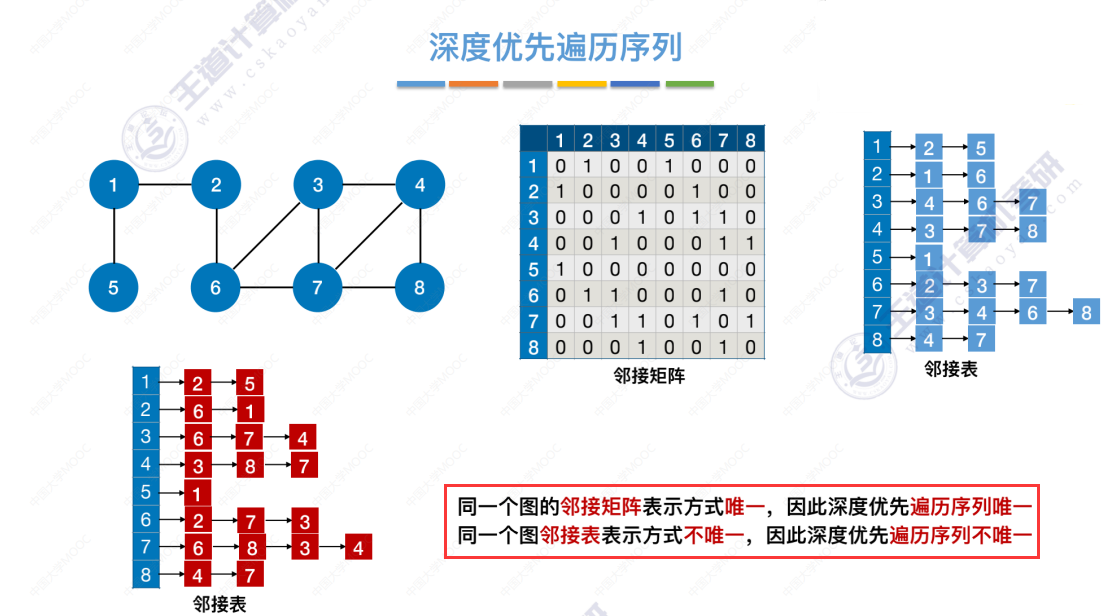
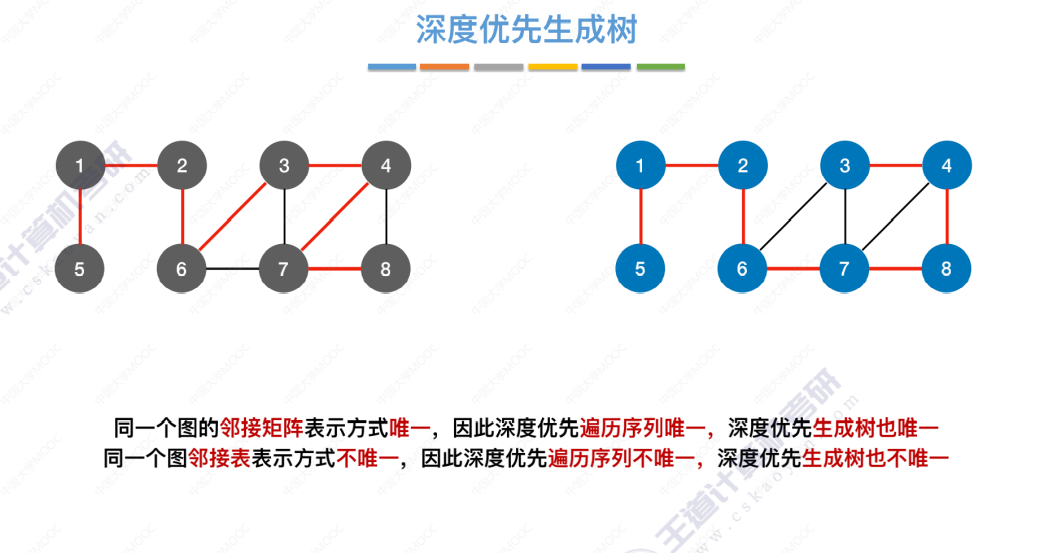
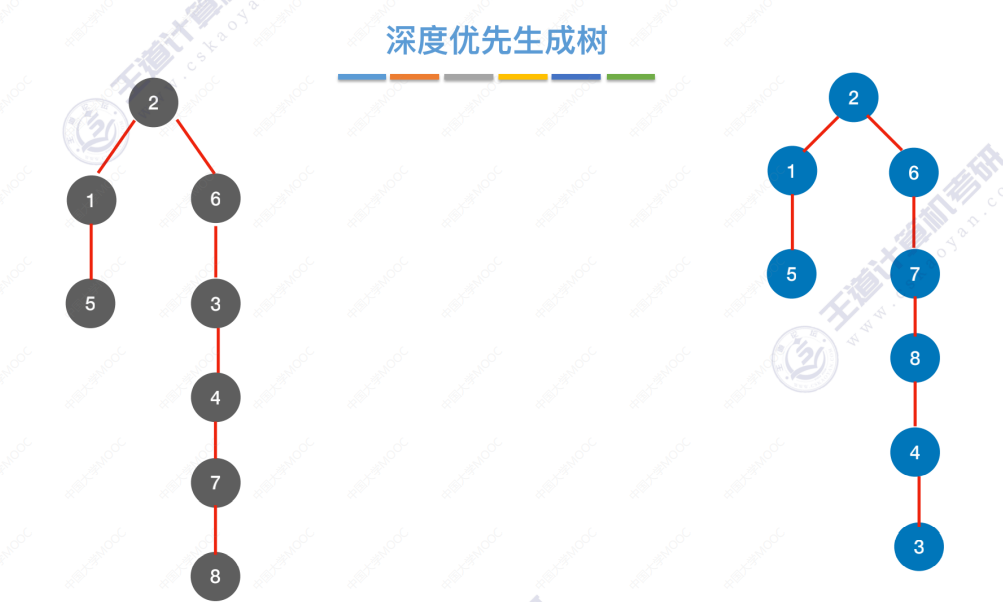
    在这里插入图片描述
    在这里插入图片描述

    深度优先生成树

    标红，当某个顶点第一次被访问时是从哪条边过去的，把标红的边 和 结点单独拿出来，未标红的边去掉，就形成了深度优先生成树。
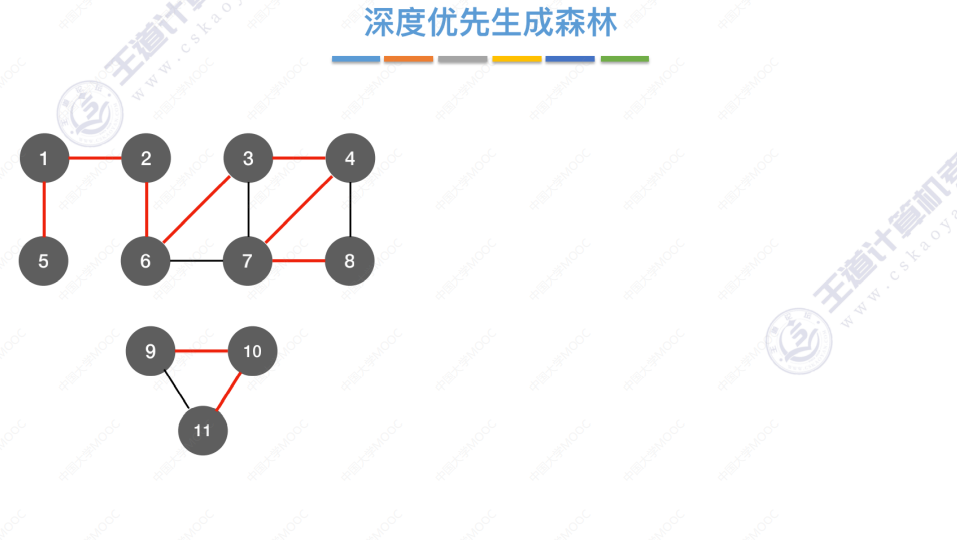
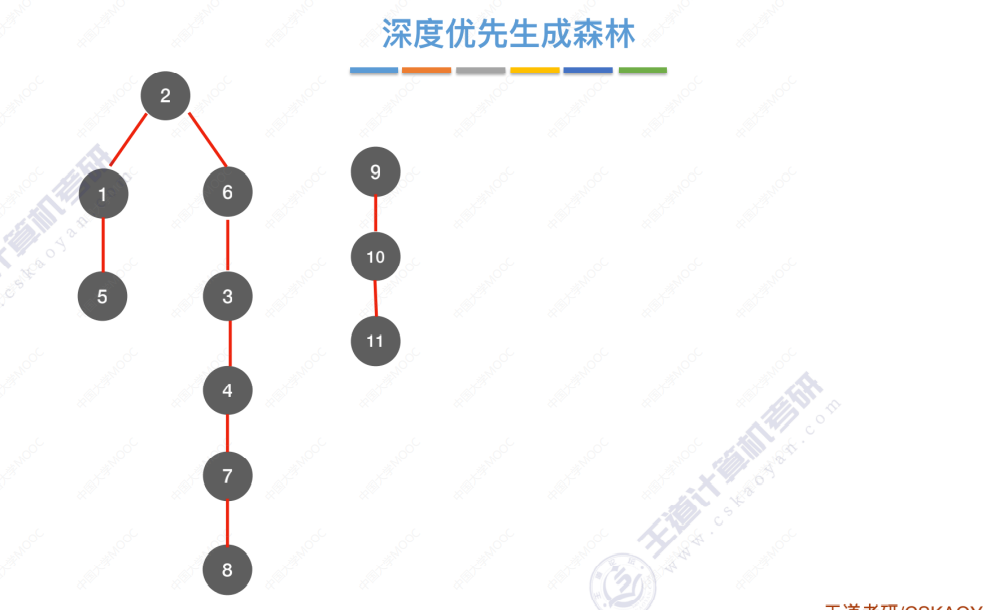
    在这里插入图片描述
    在这里插入图片描述

    深度优先生成森林

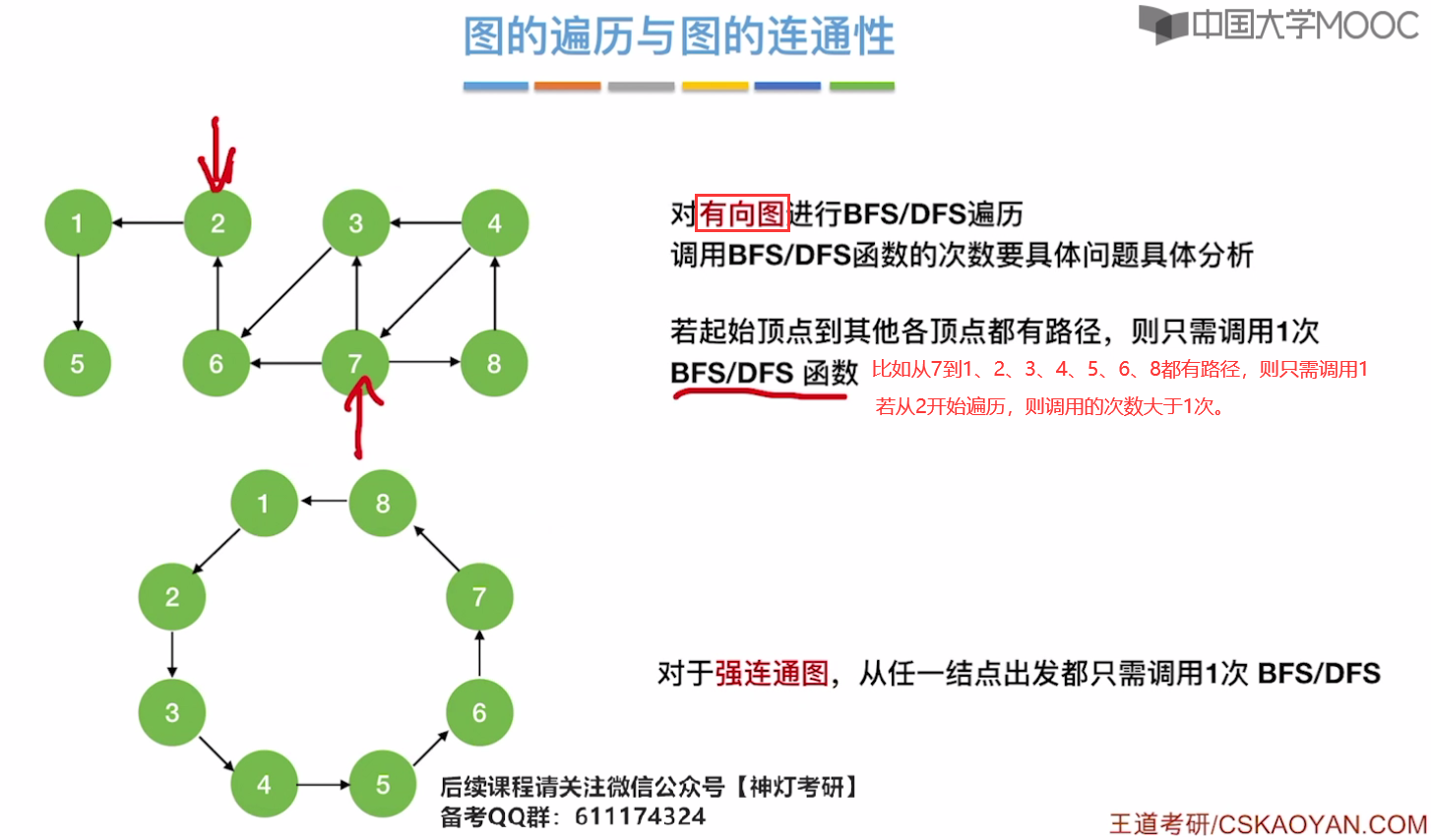
    在这里插入图片描述
    在这里插入图片描述

    图的遍历和图的连通性

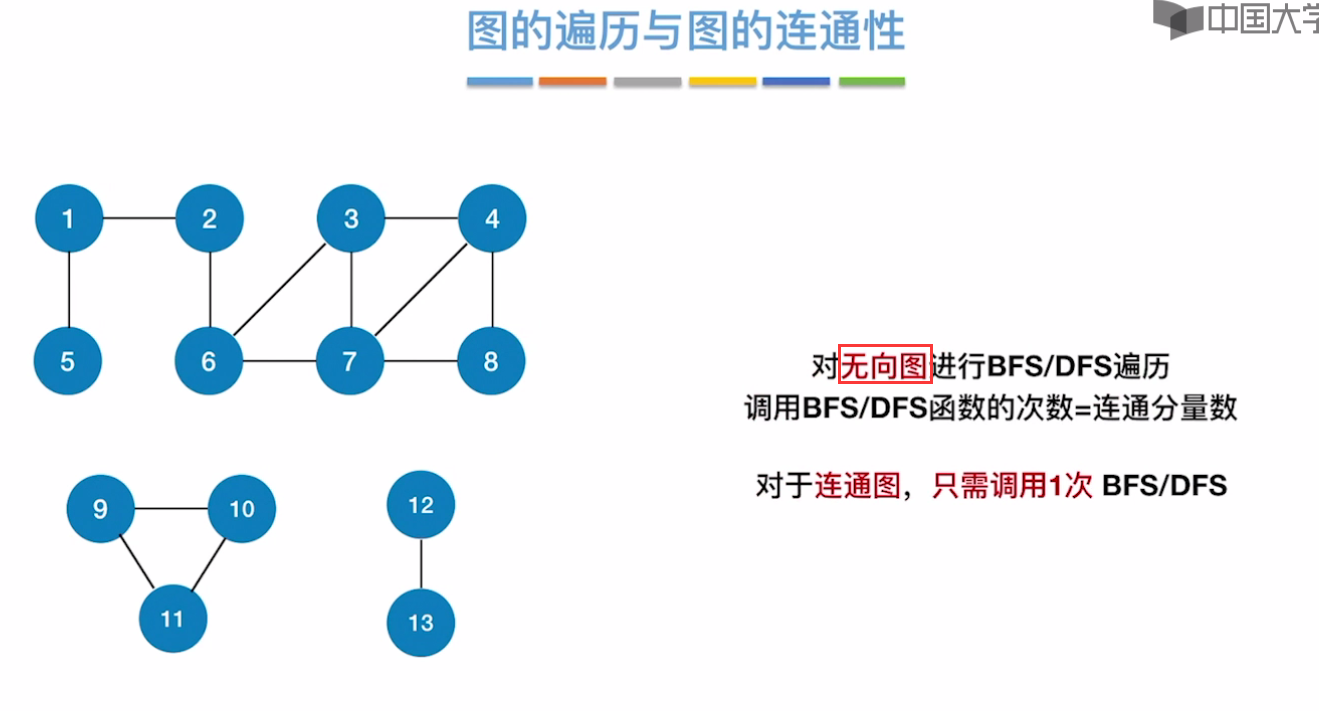
    在这里插入图片描述
    下图，如果7仅仅能和邻接顶点6、3、8有路径而和其余顶点5、1、2、4没有路径，那么调用次数也是要多于1次的。
    在这里插入图片描述

    6.4-1 最小生成树

    生成树是什么


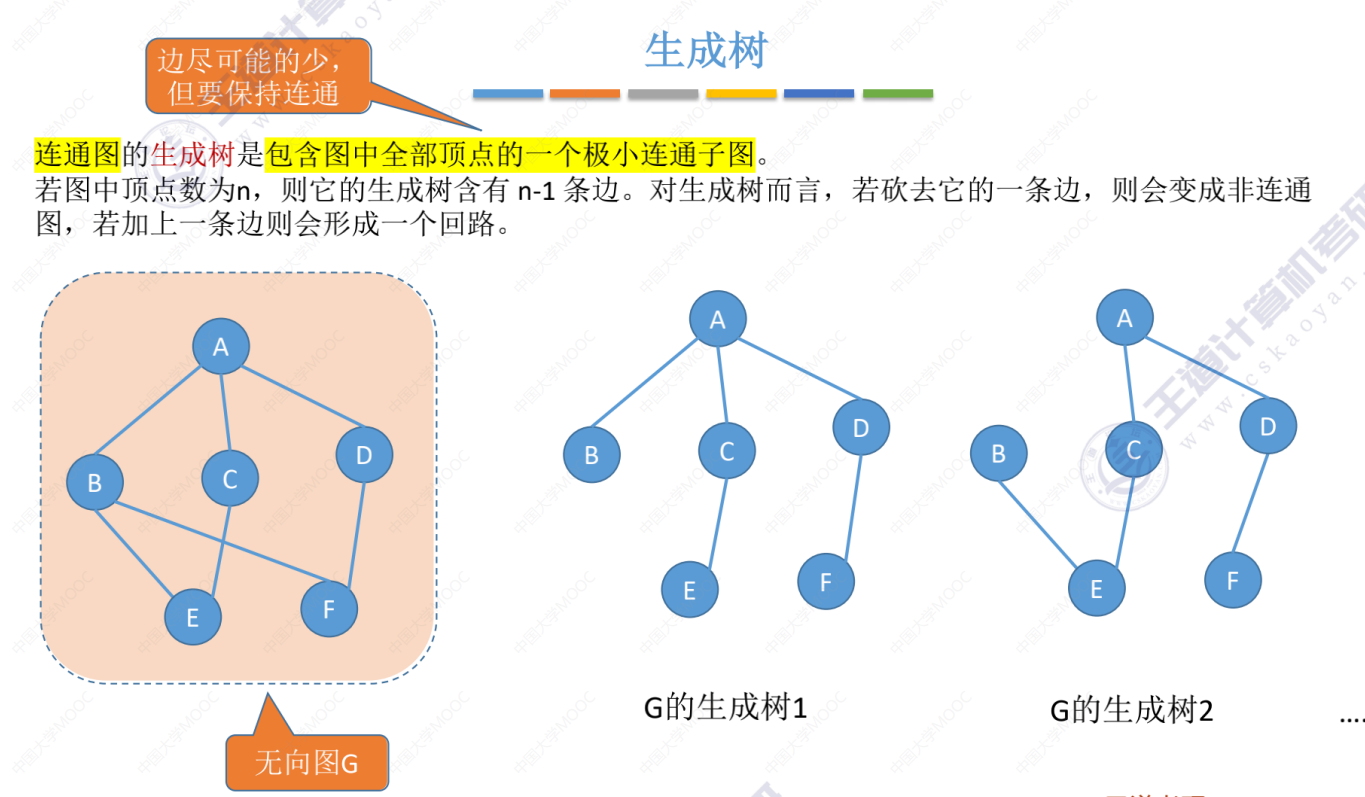
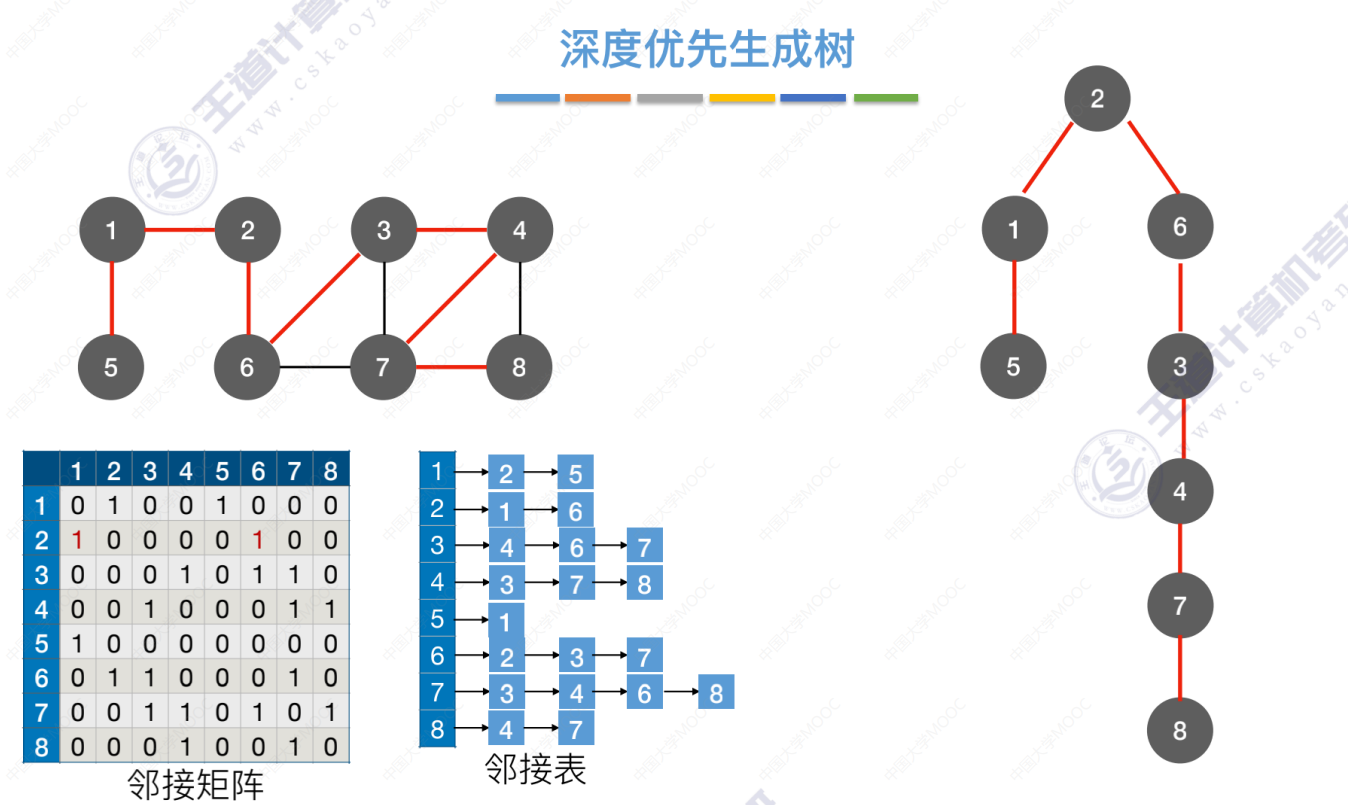
    在这里插入图片描述
    在这里插入图片描述

    最小生成树

    带权、连通、无向
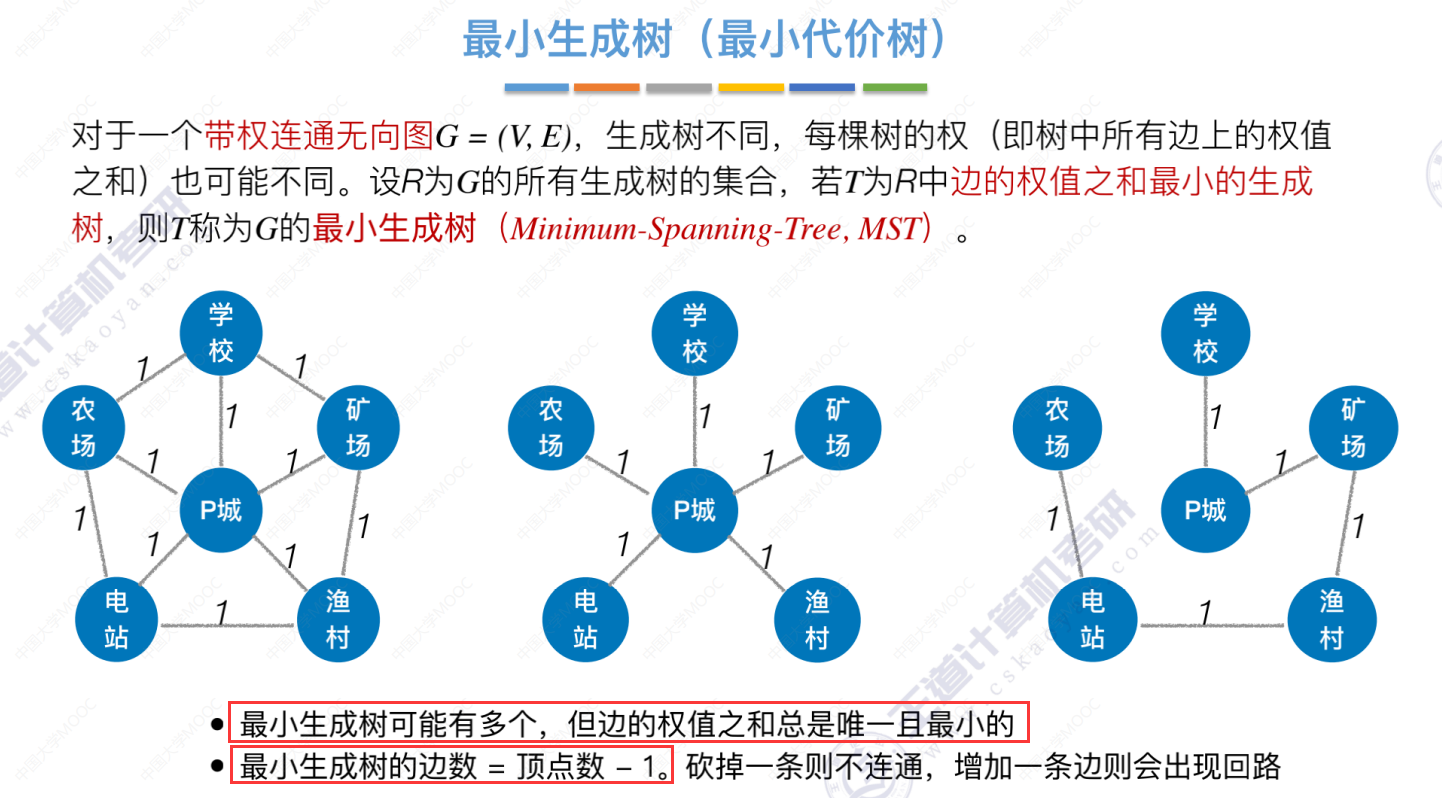
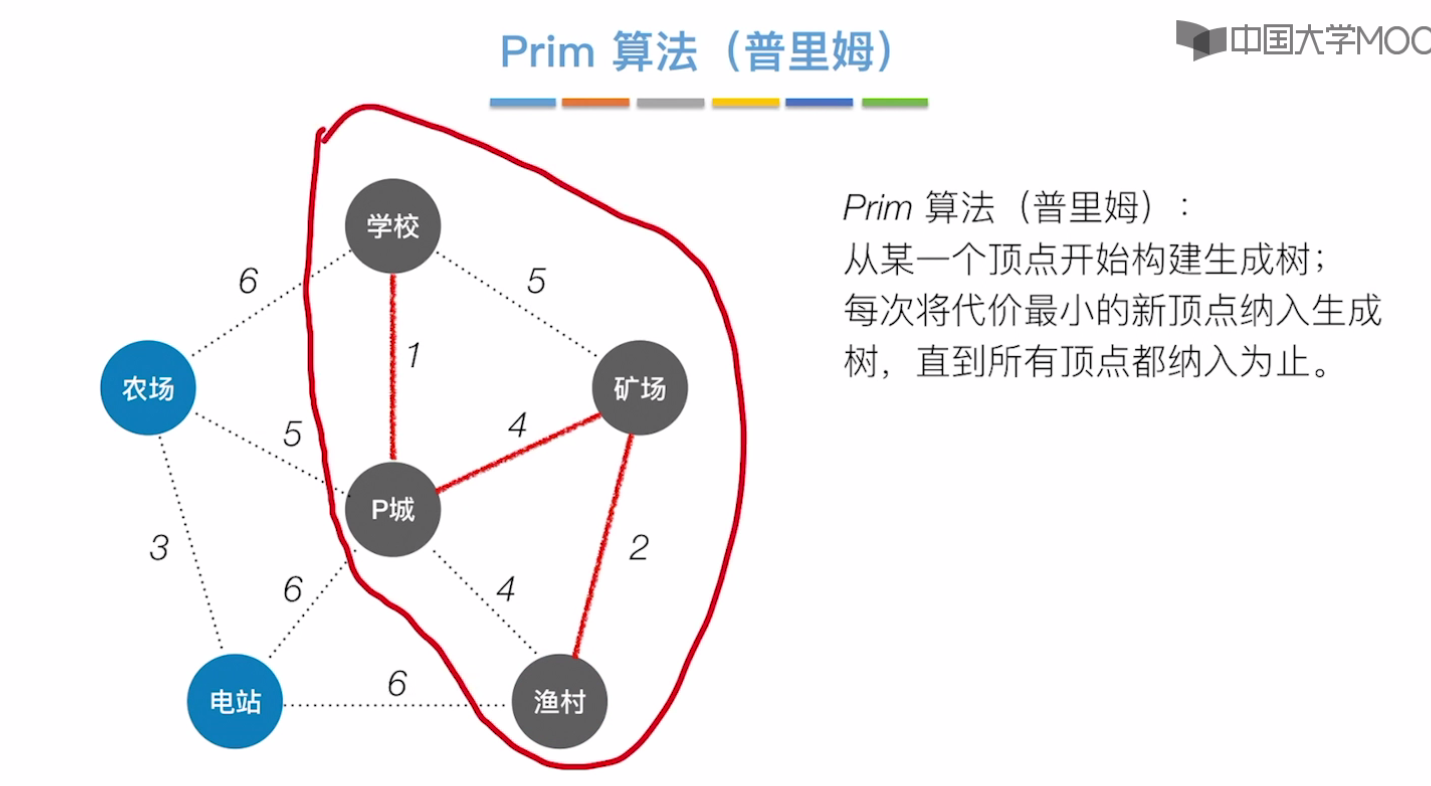
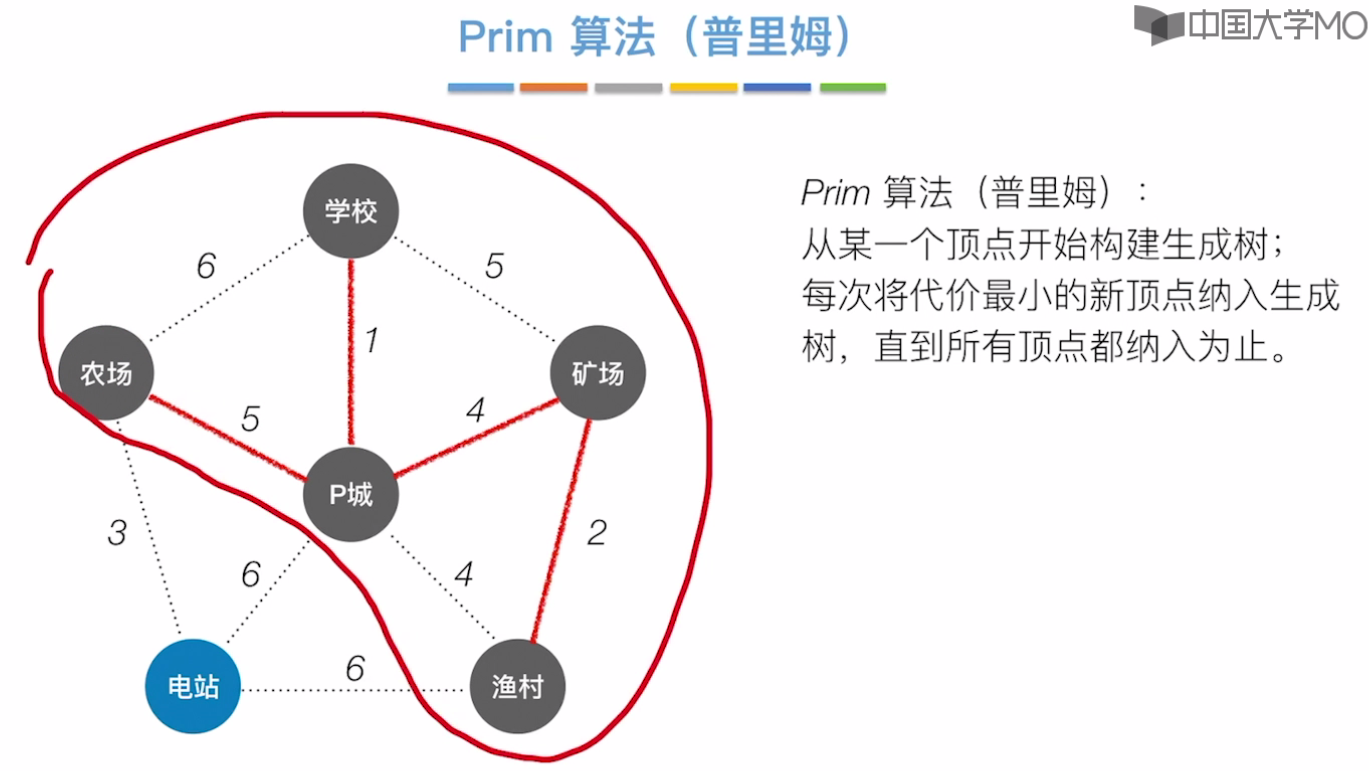
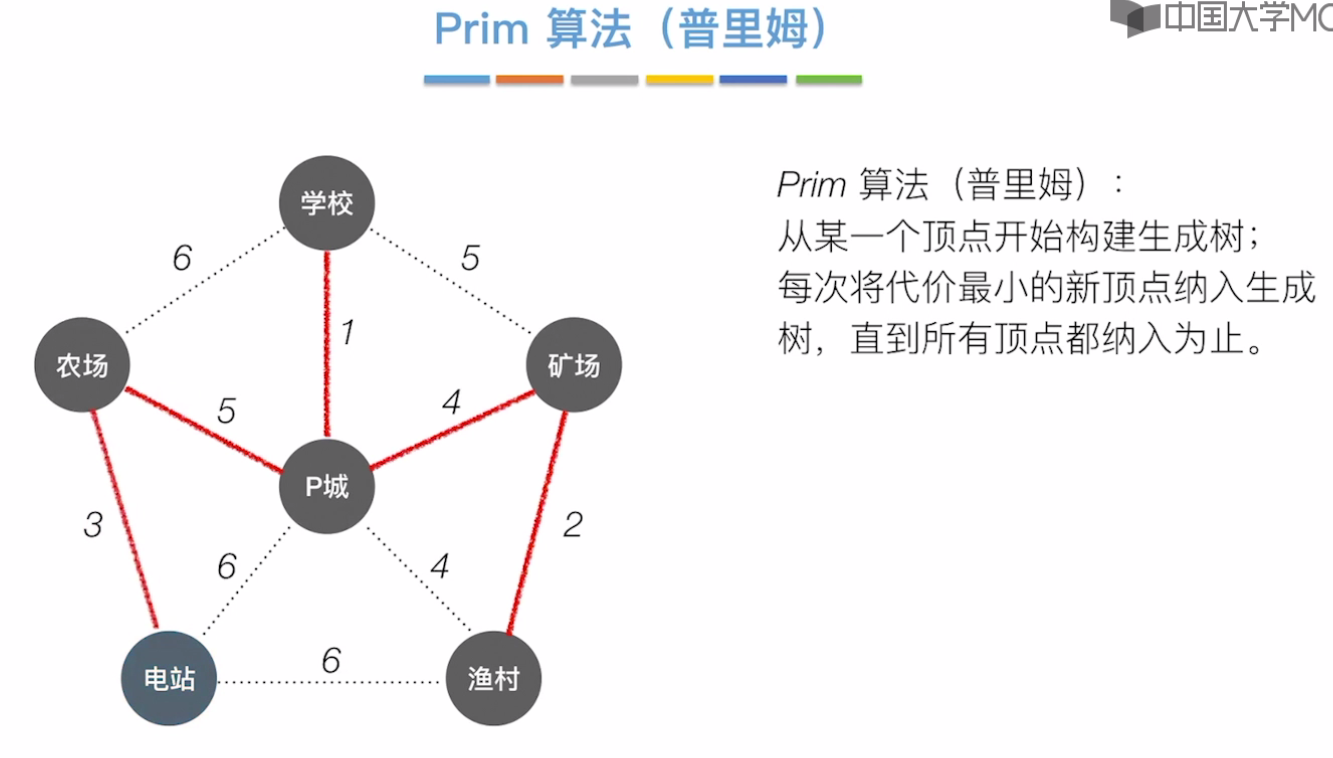
    在这里插入图片描述
    在这里插入图片描述

    Prim算法

    从p城出发

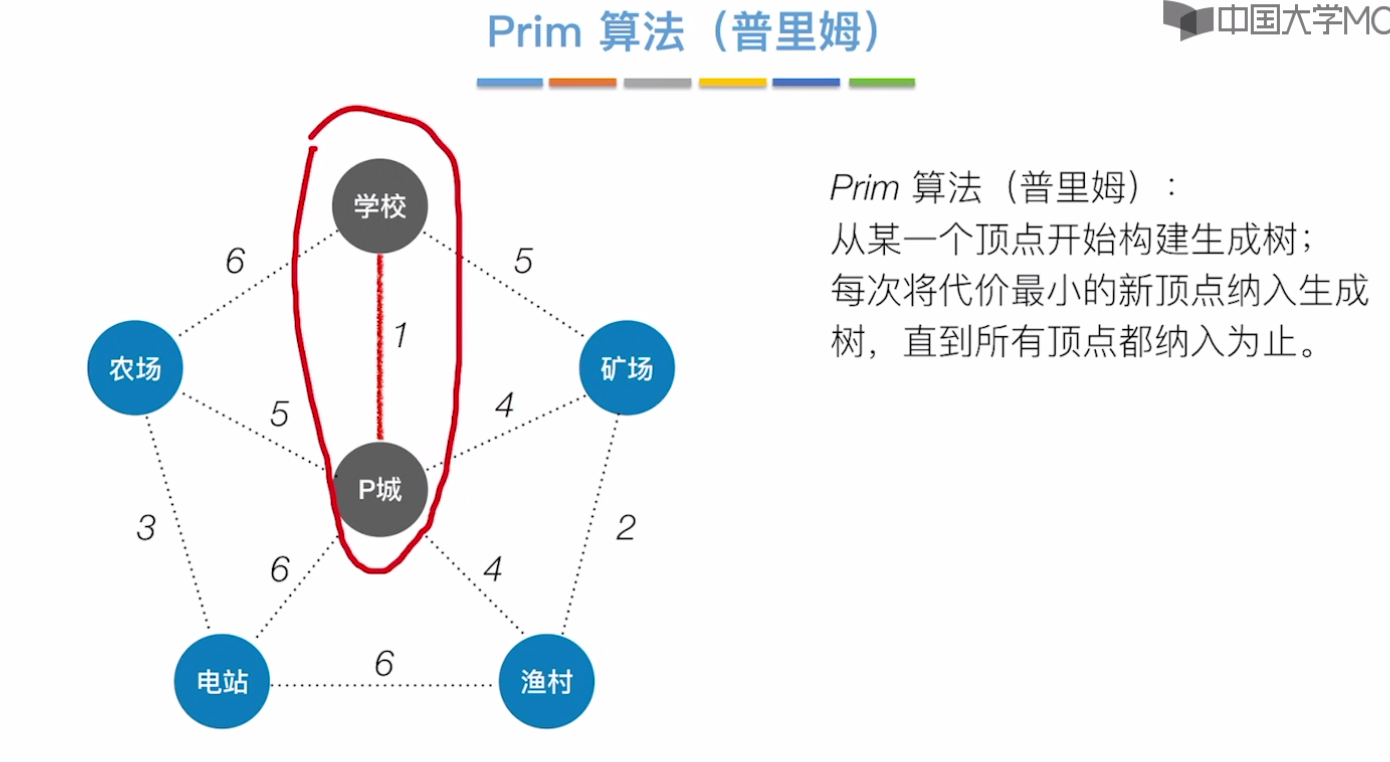
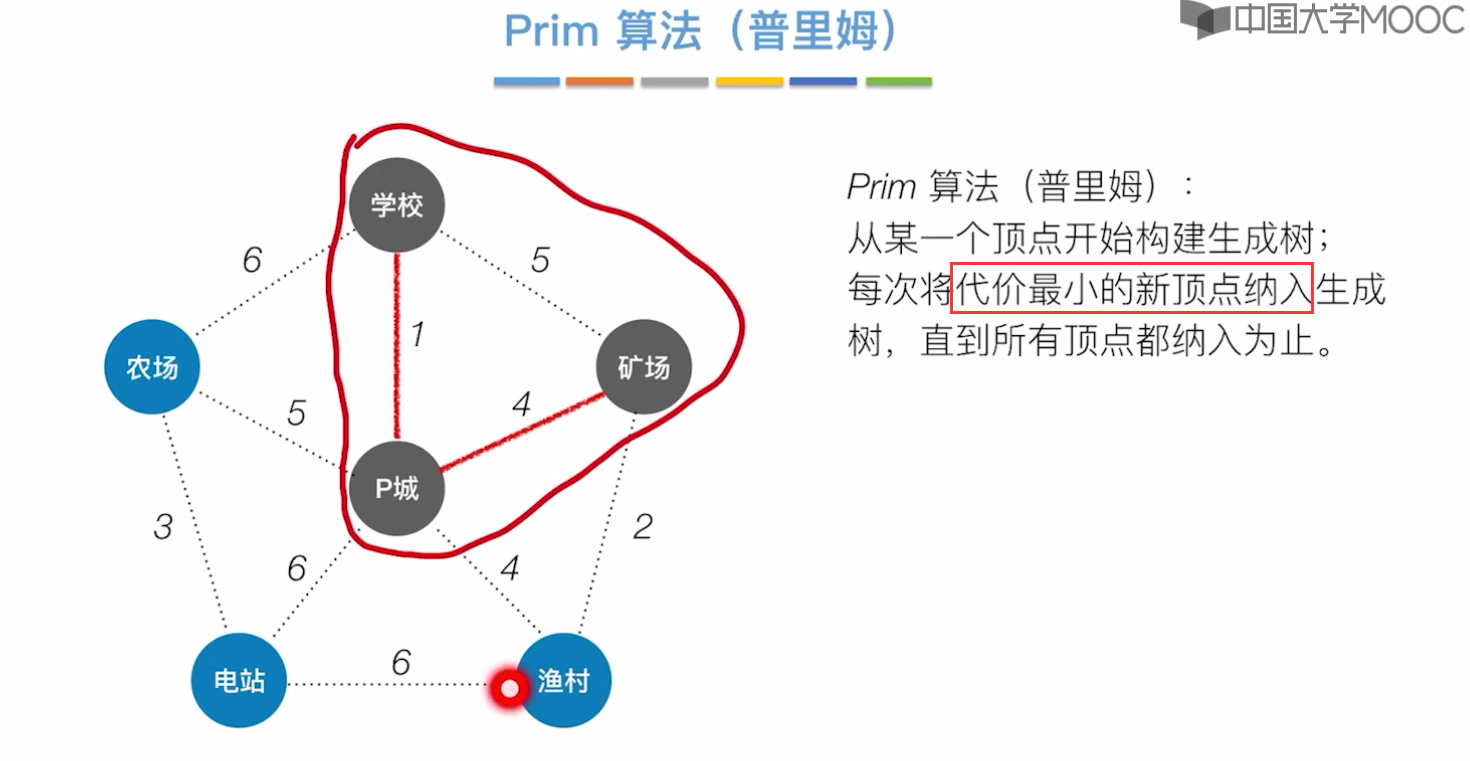
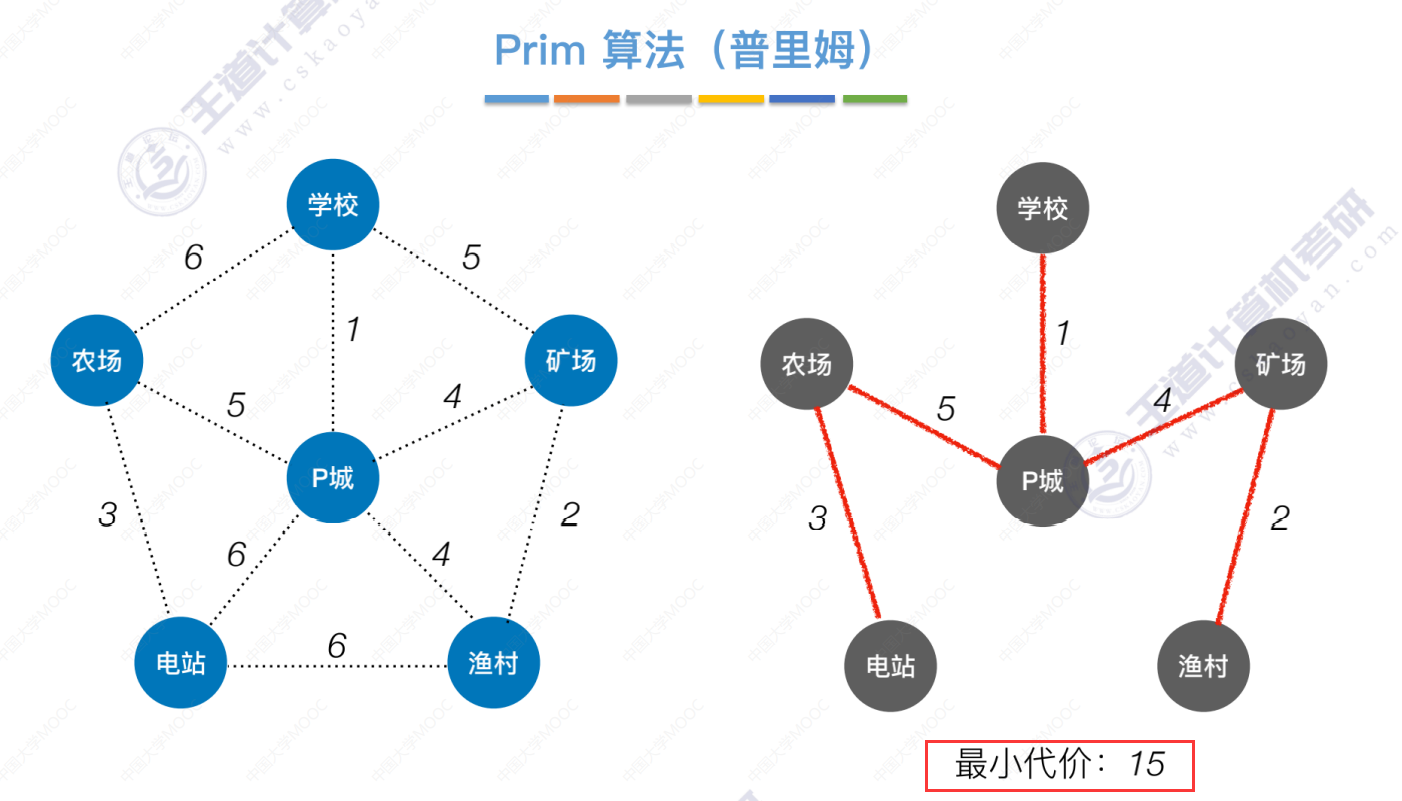
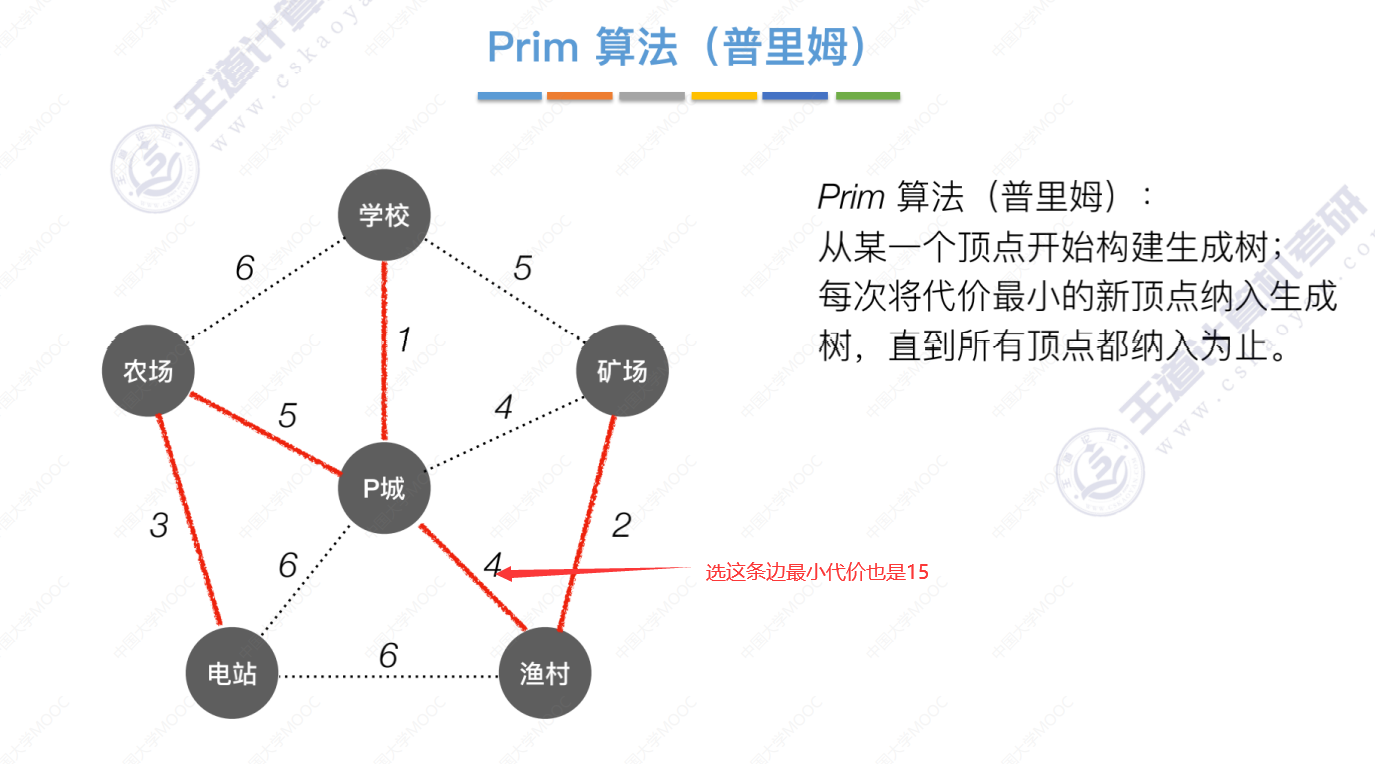
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述

    从农场出发

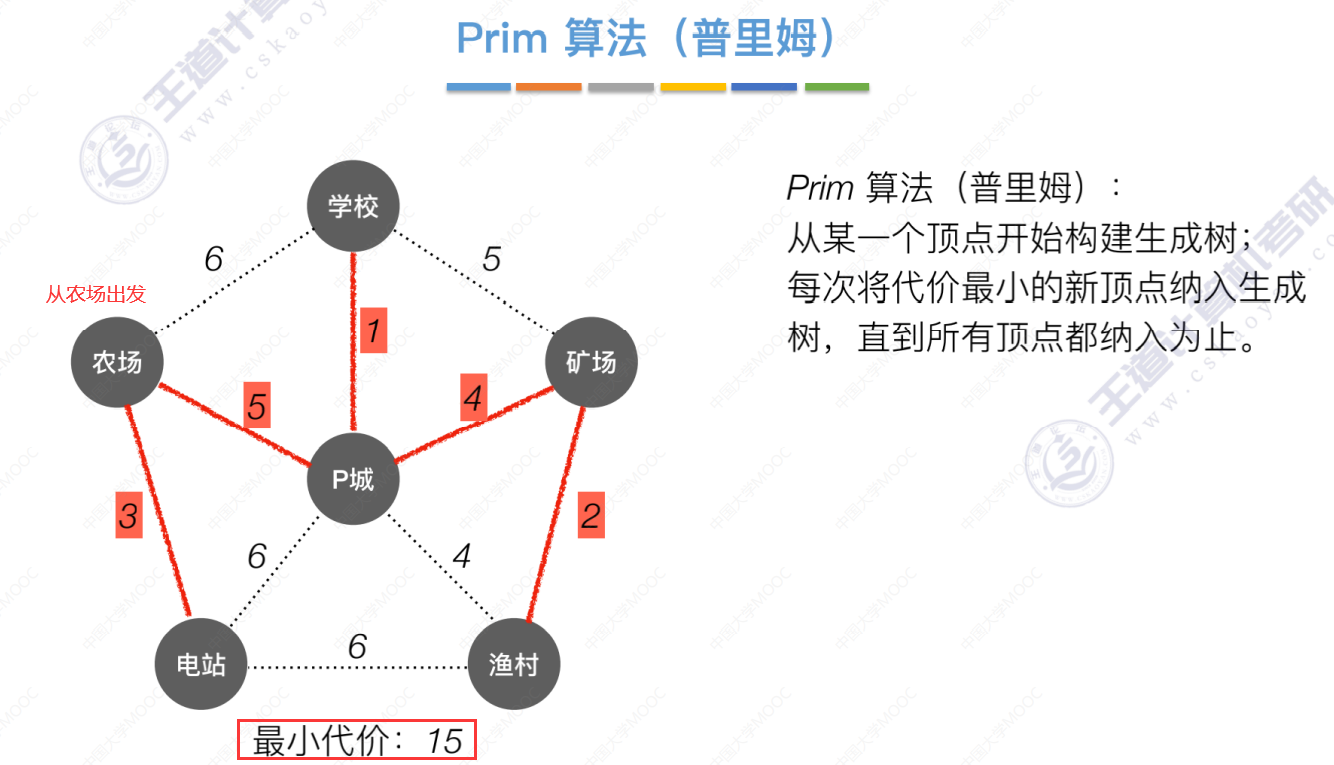
    在这里插入图片描述

    Kruskal算法

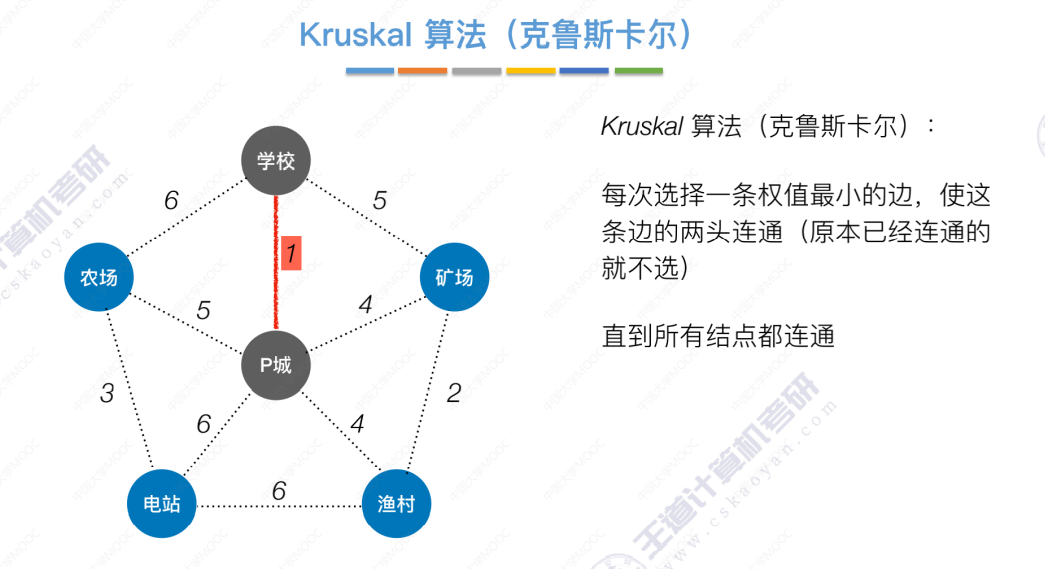
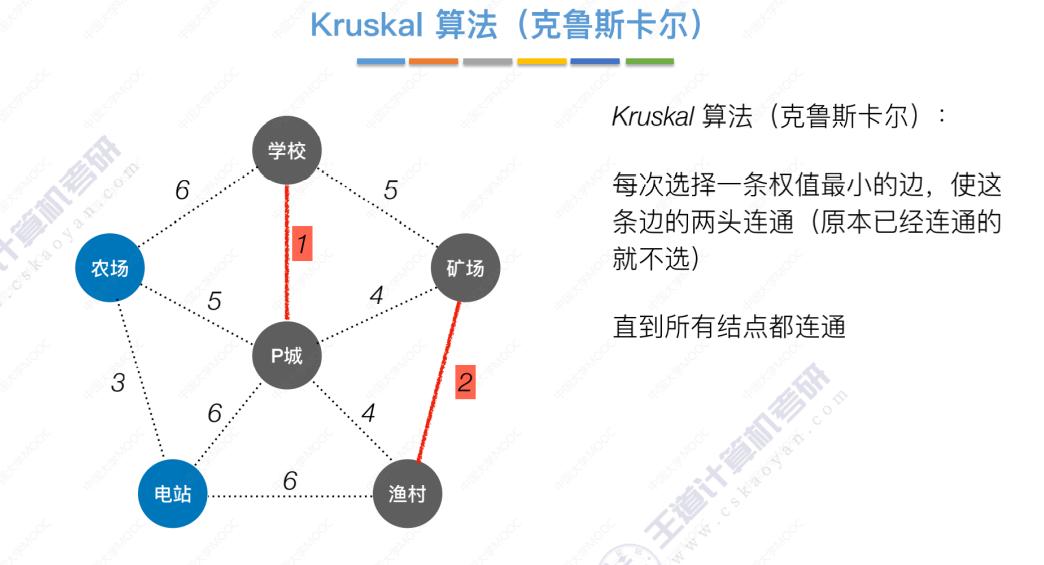
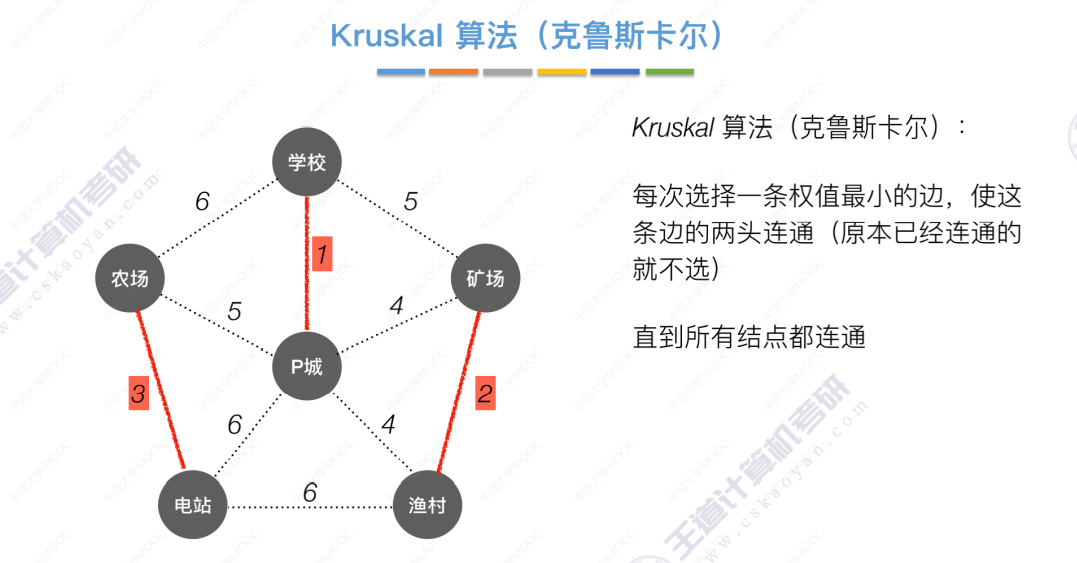
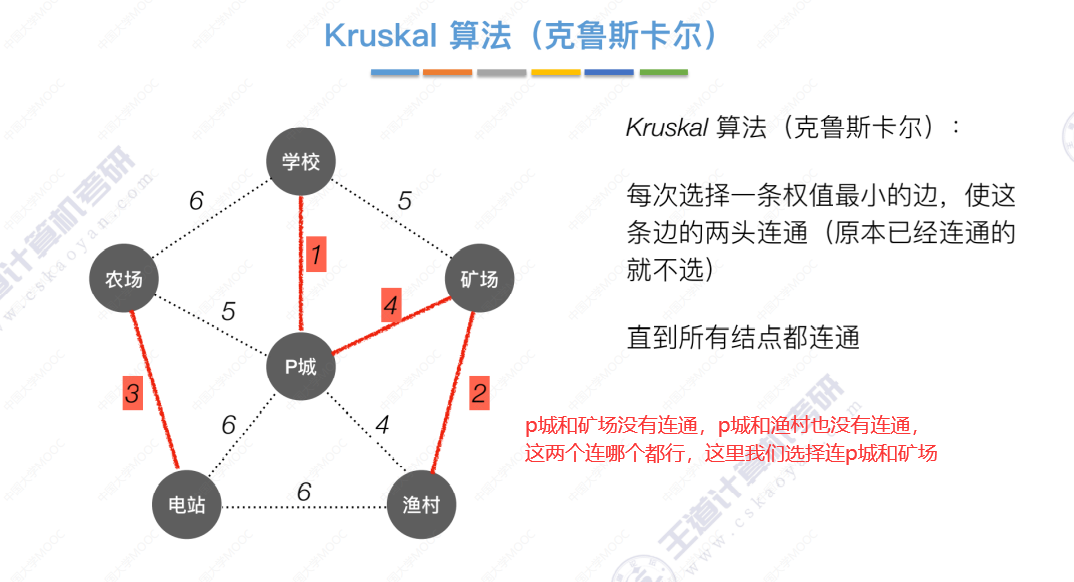
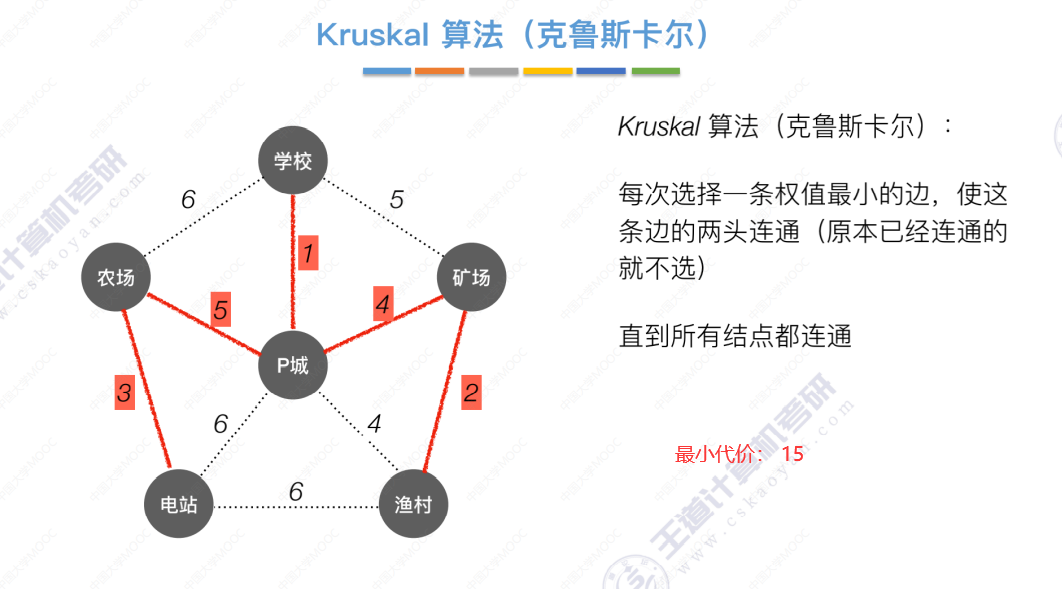
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    直到所有结点都连通，算法结束。

    Prim算法和Kruskal算法对比

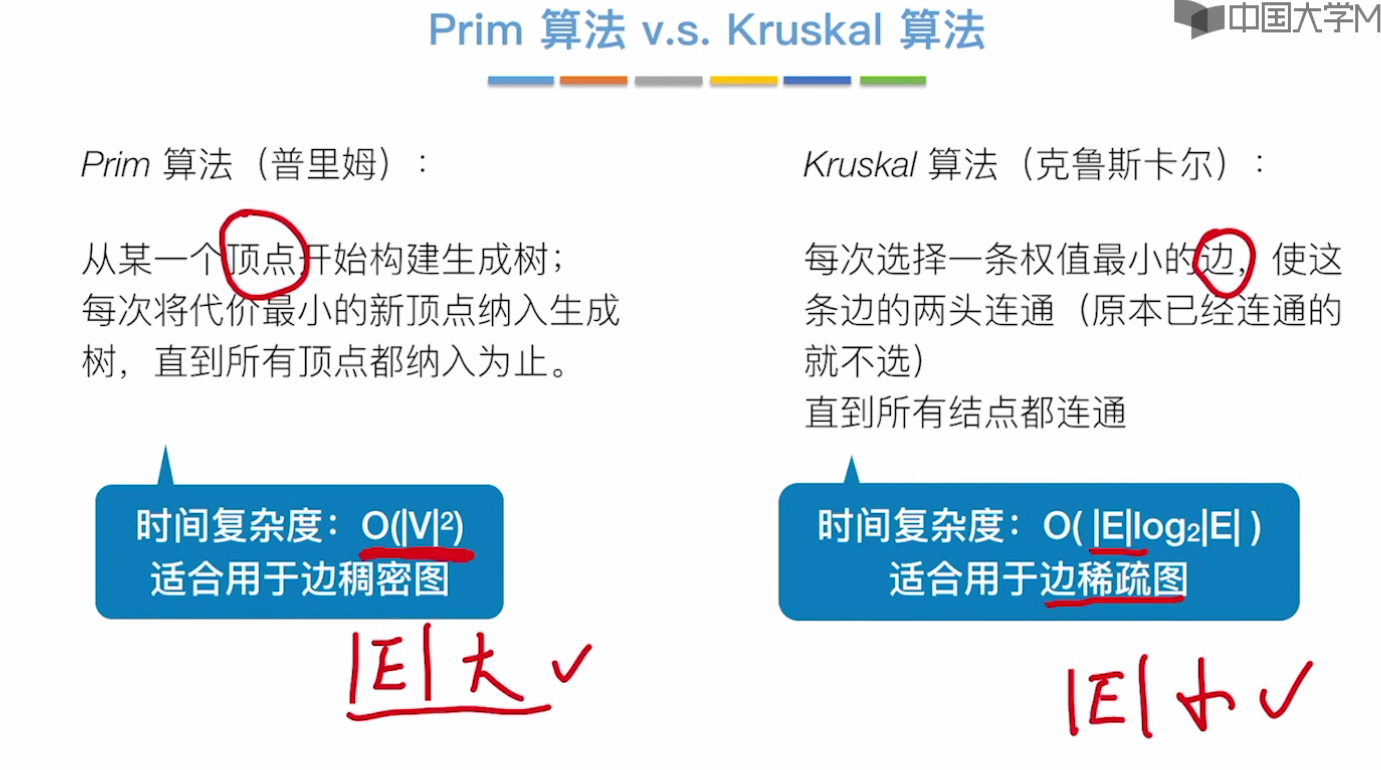
    在这里插入图片描述

    6.4-2 最短路径问题_BFS算法

    最短路径问题介绍

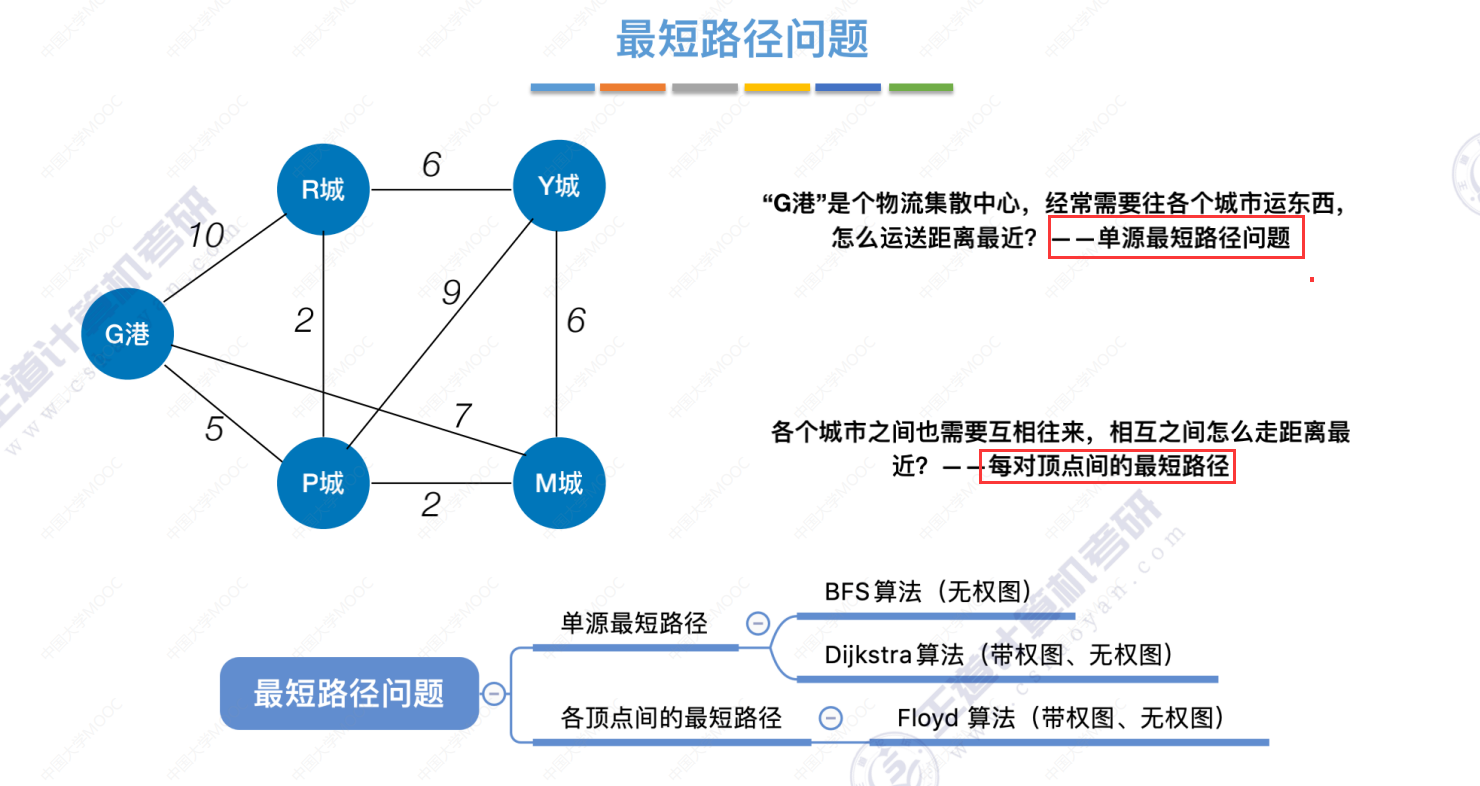
    在这里插入图片描述

    BFS(广度优先求最短路径)

    BFS算法求单源最短路径只适用于无权图，或所有边的权值都相同的图。

    引入

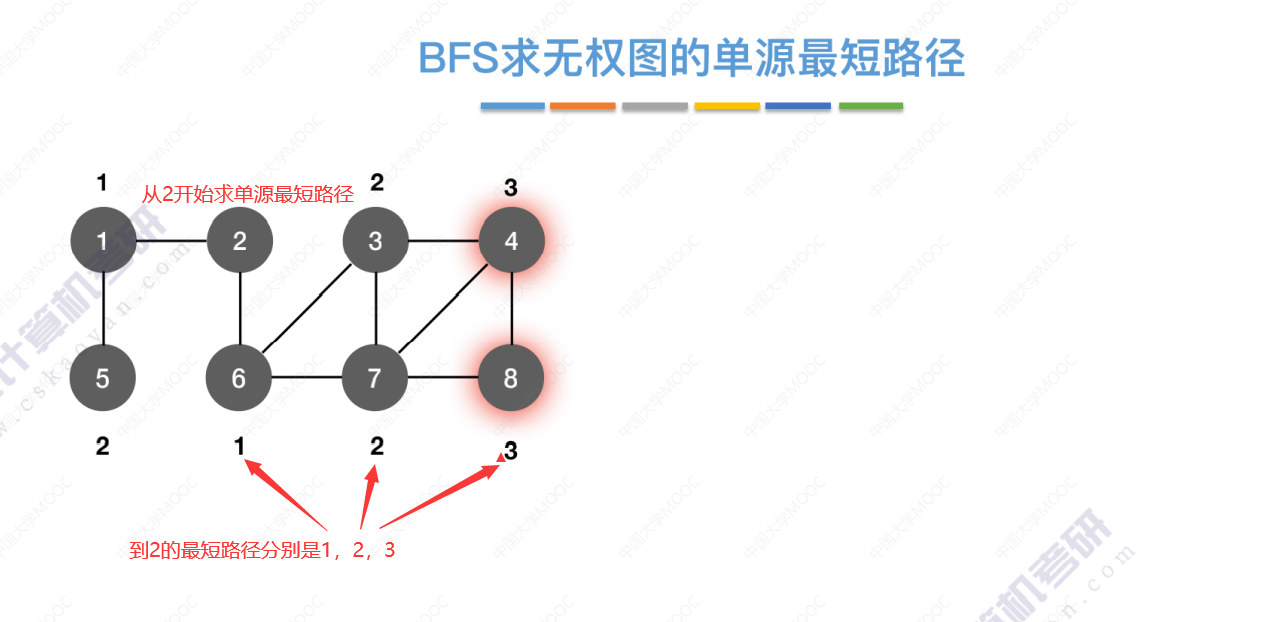
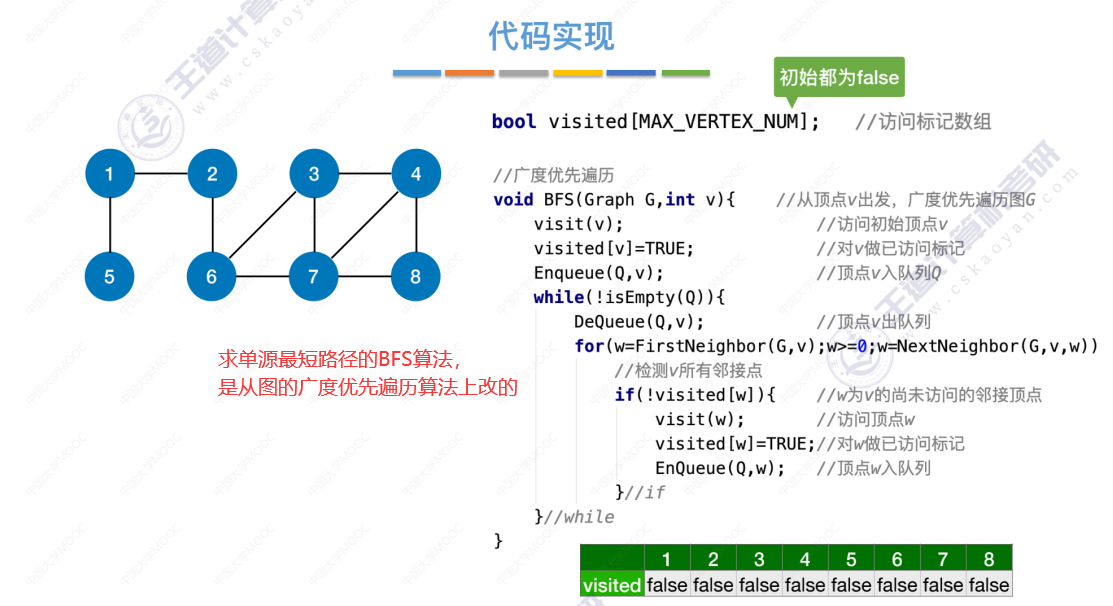
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述

    BFS求无权图的单源最短路径的代码实现

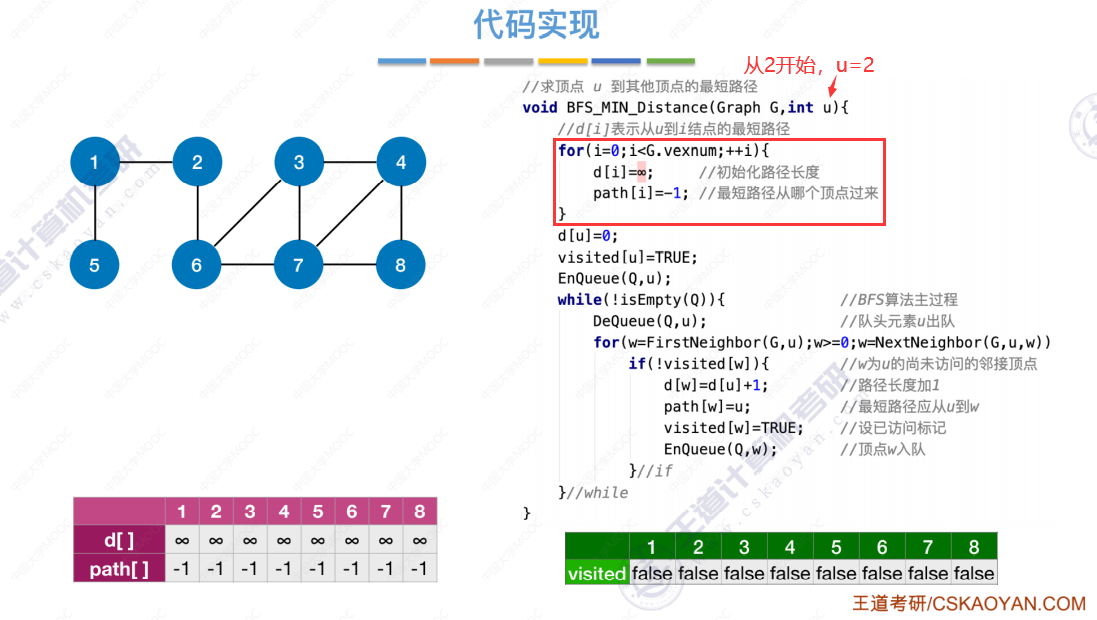
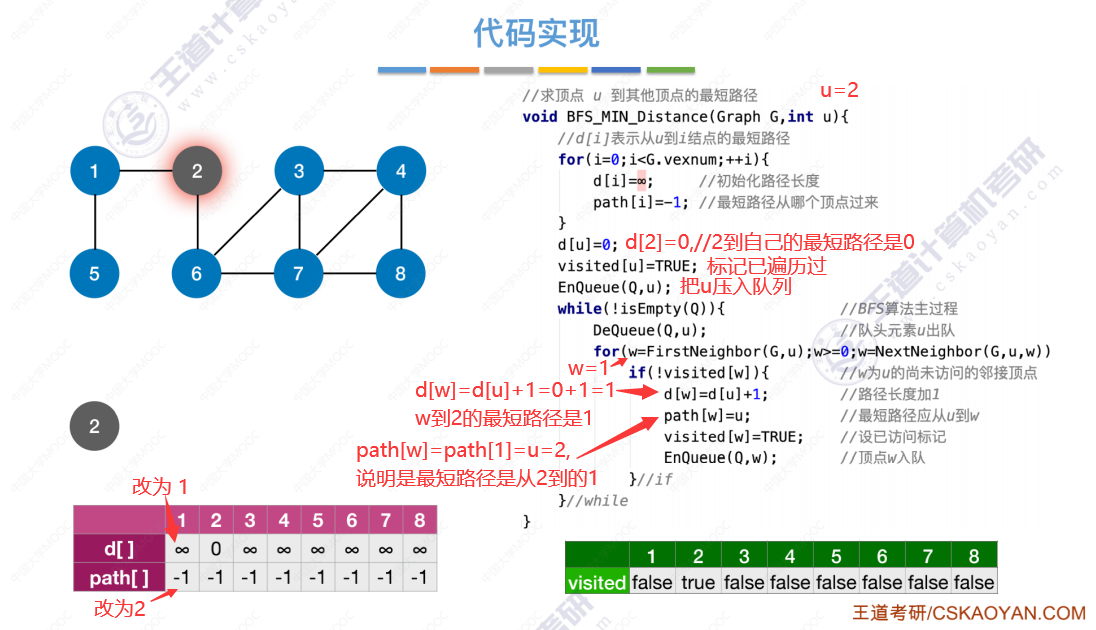
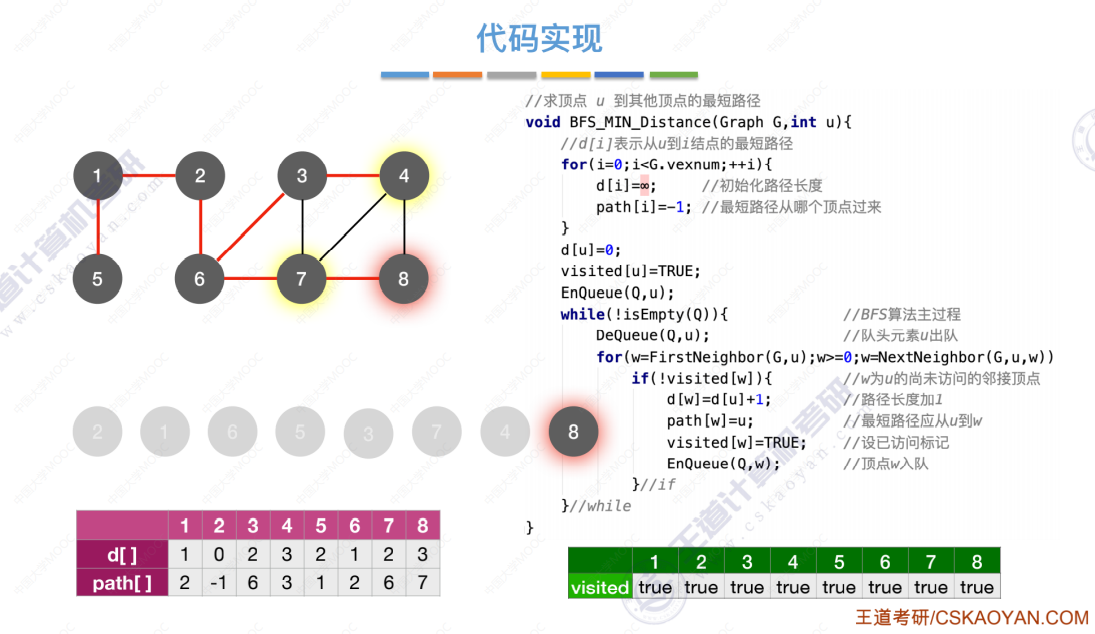
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    按照最短路径的求解方法生成的树，高度一定是最小的。
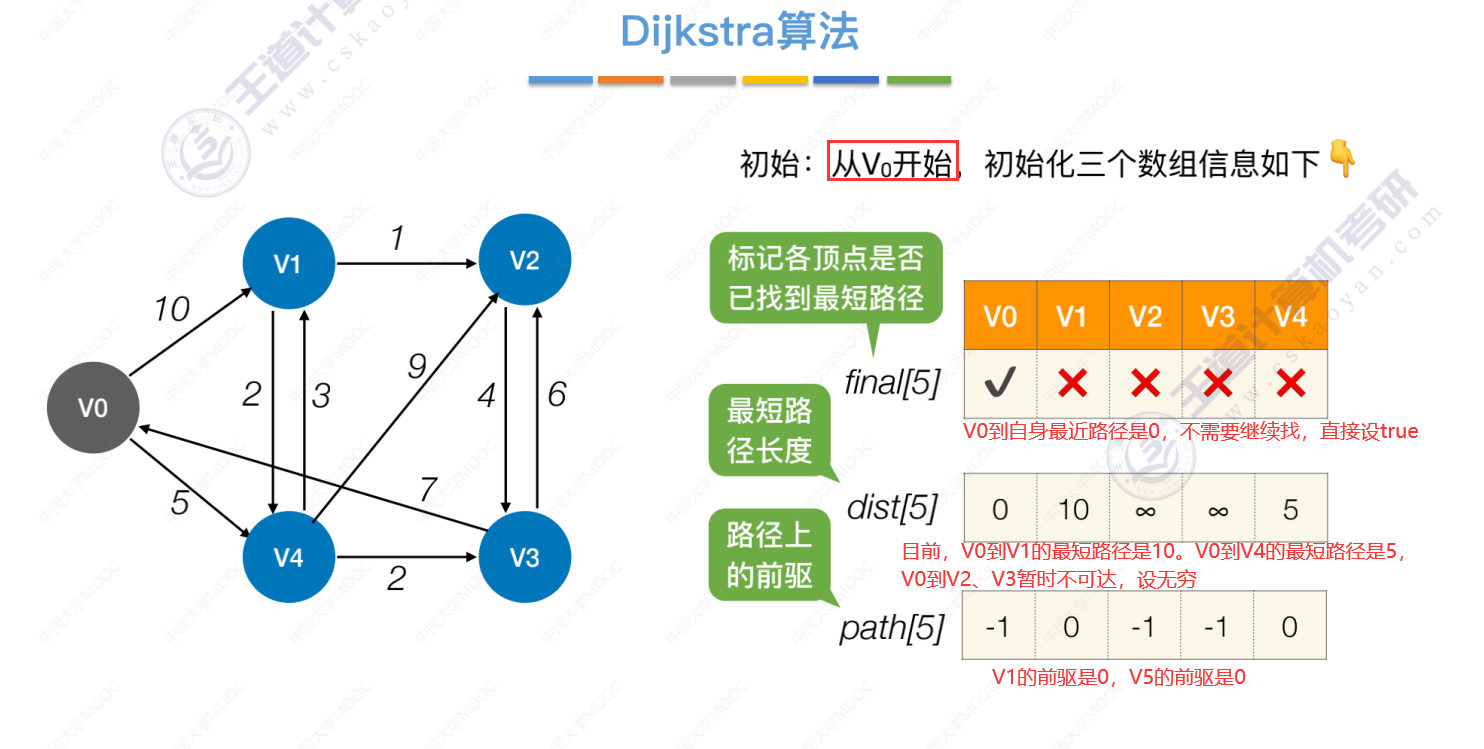
    在这里插入图片描述

    6.4-3 最短路径问题_Dijkstra算法（迪杰斯特拉算法）

    Dijkstra算法过程

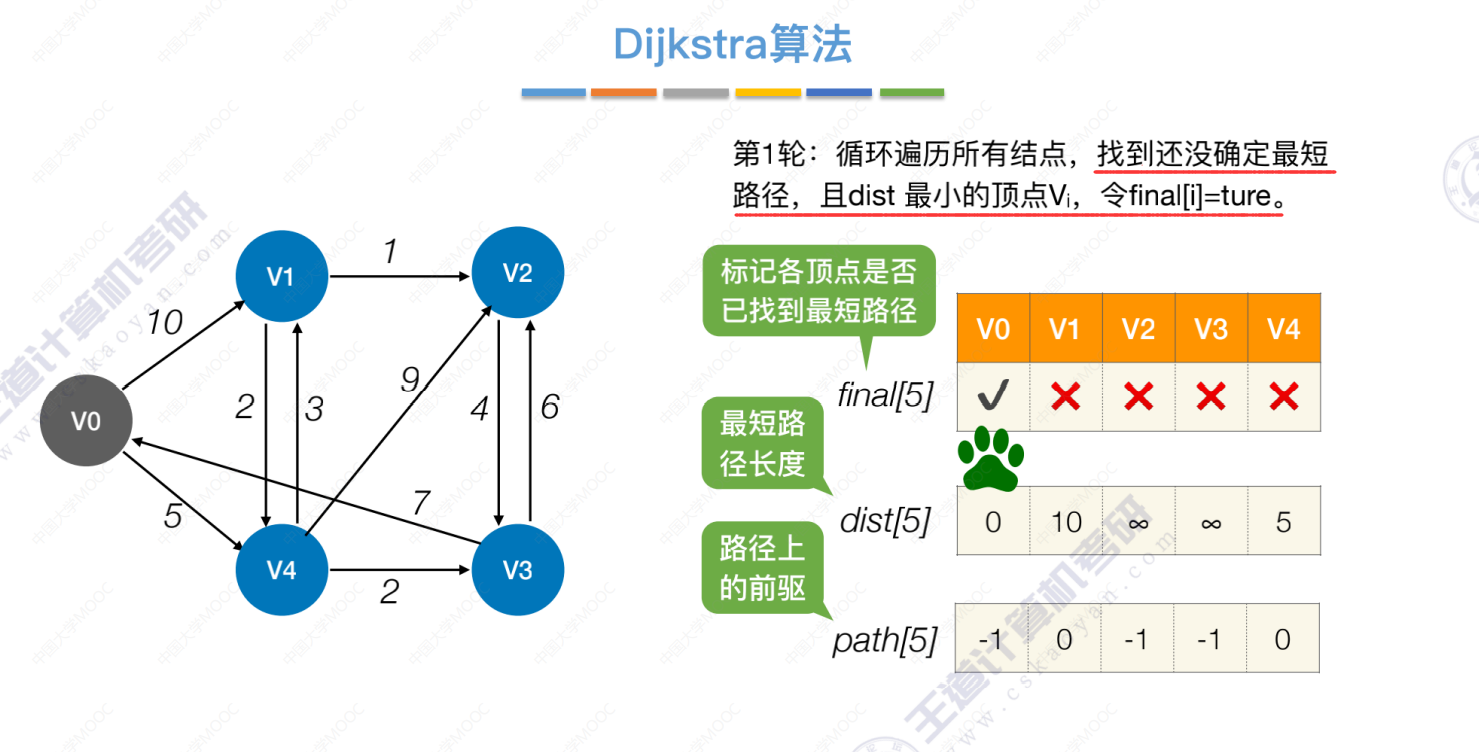
    初始化

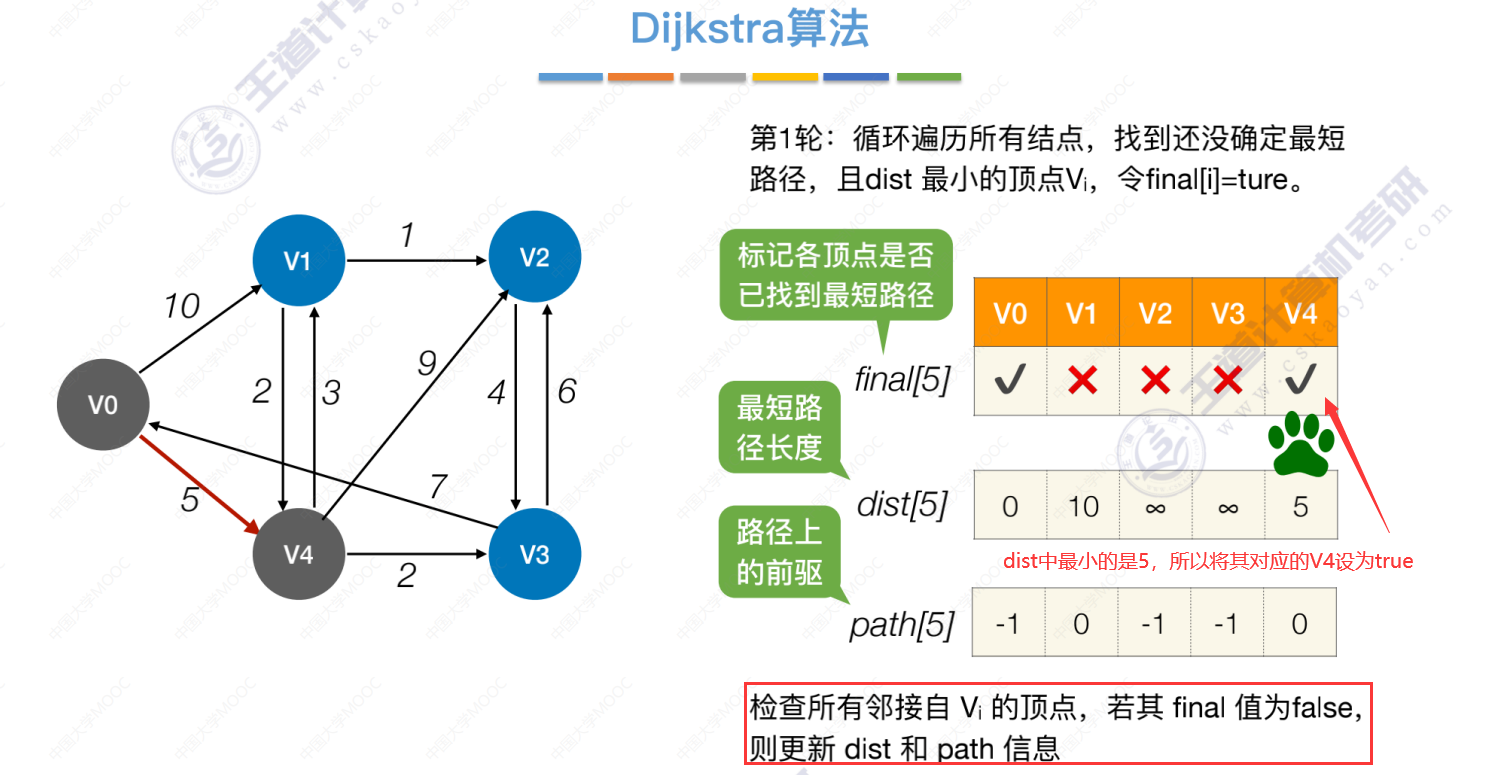
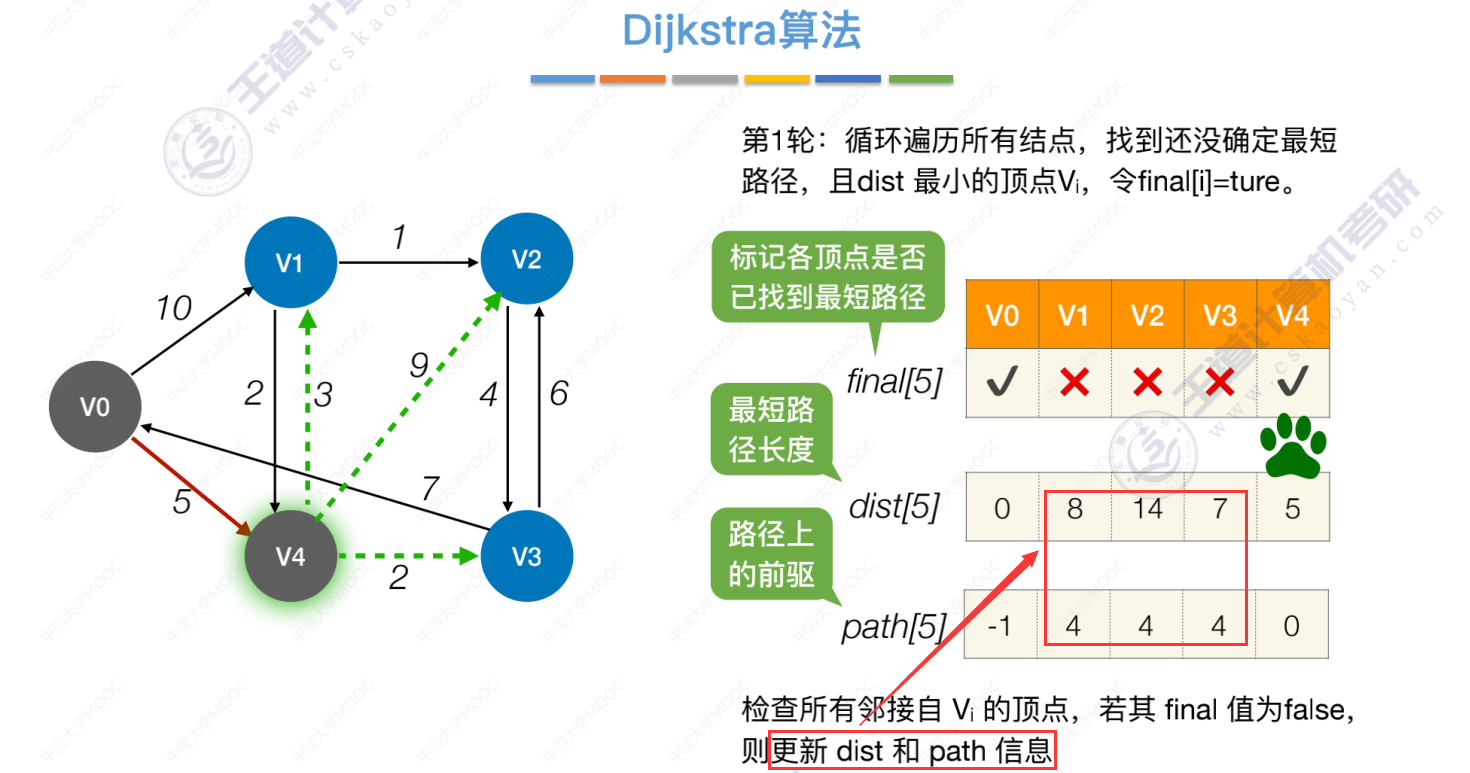
    在这里插入图片描述

    第1轮

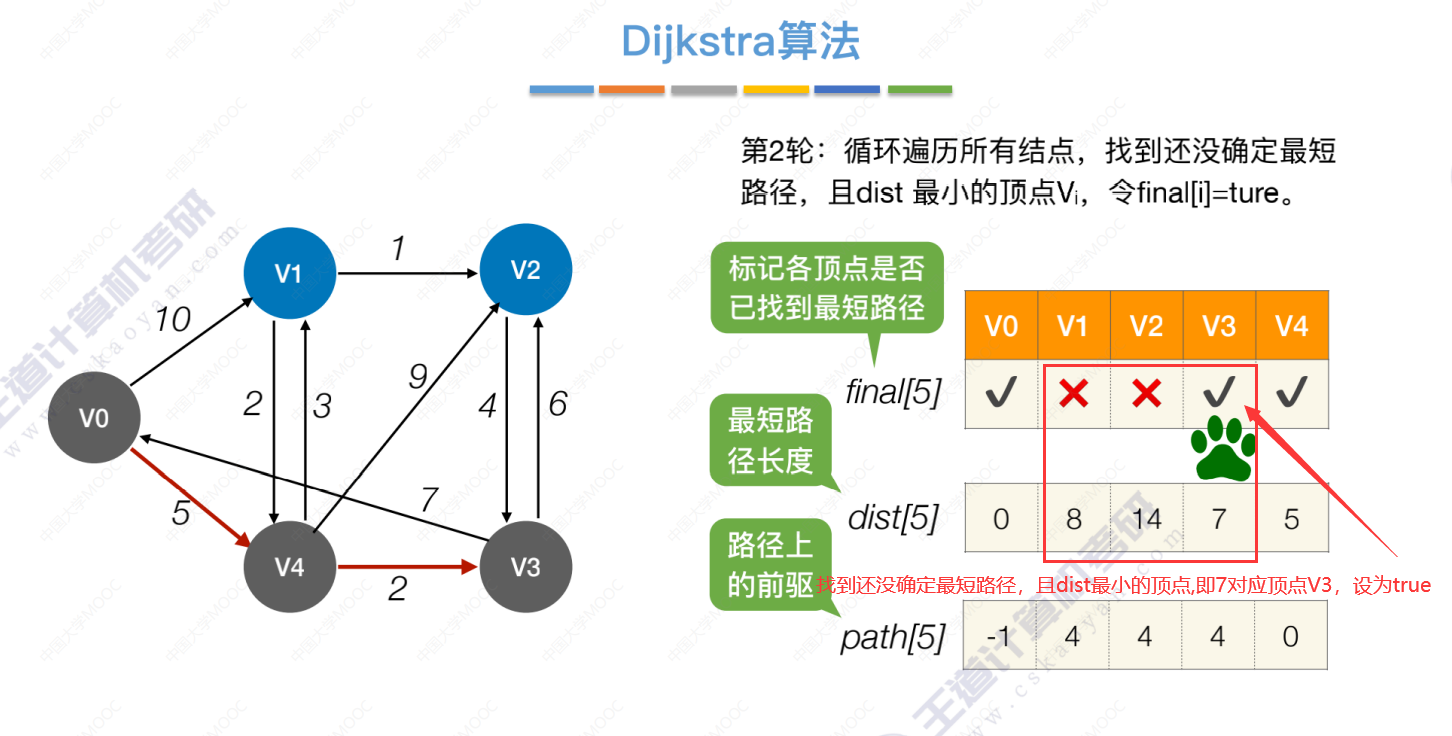
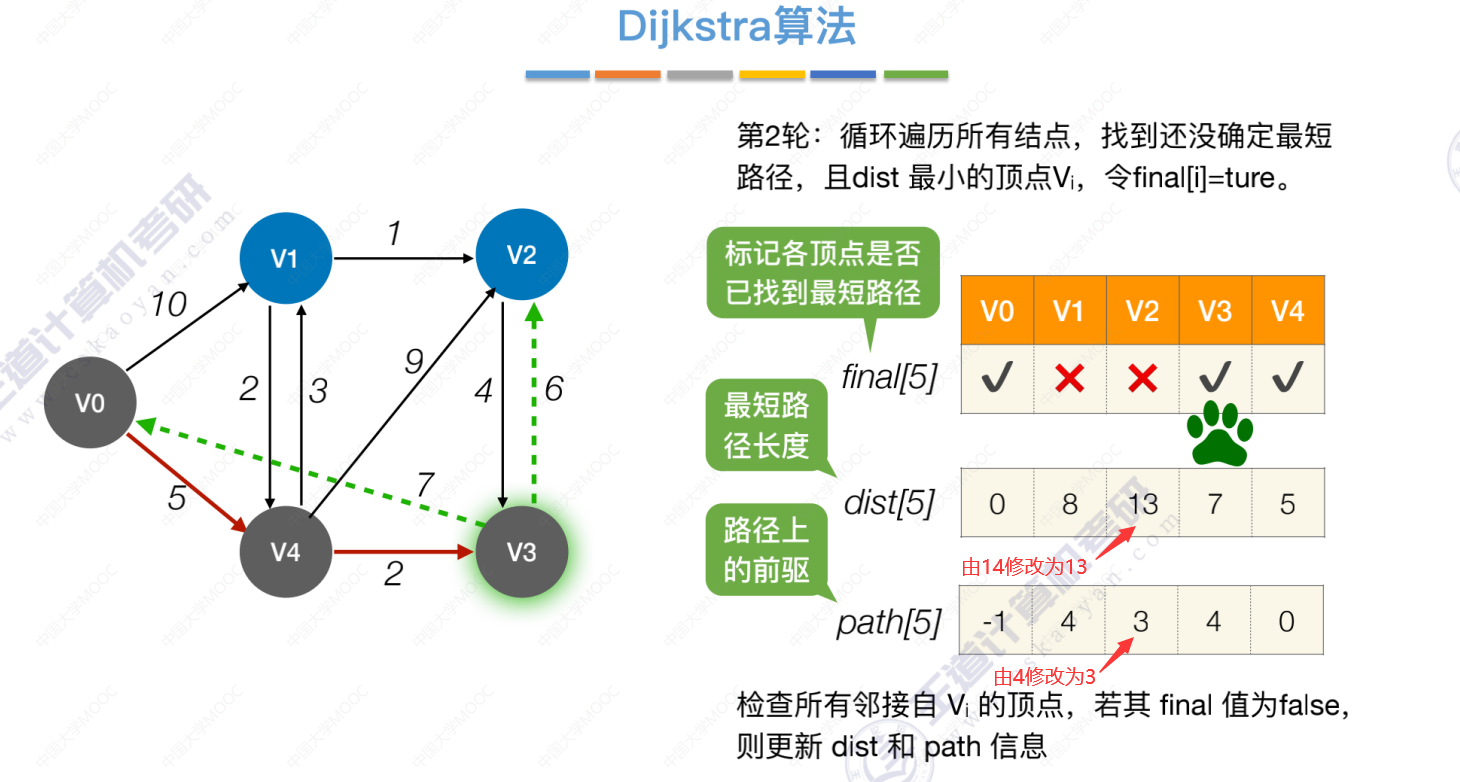
    在这里插入图片描述
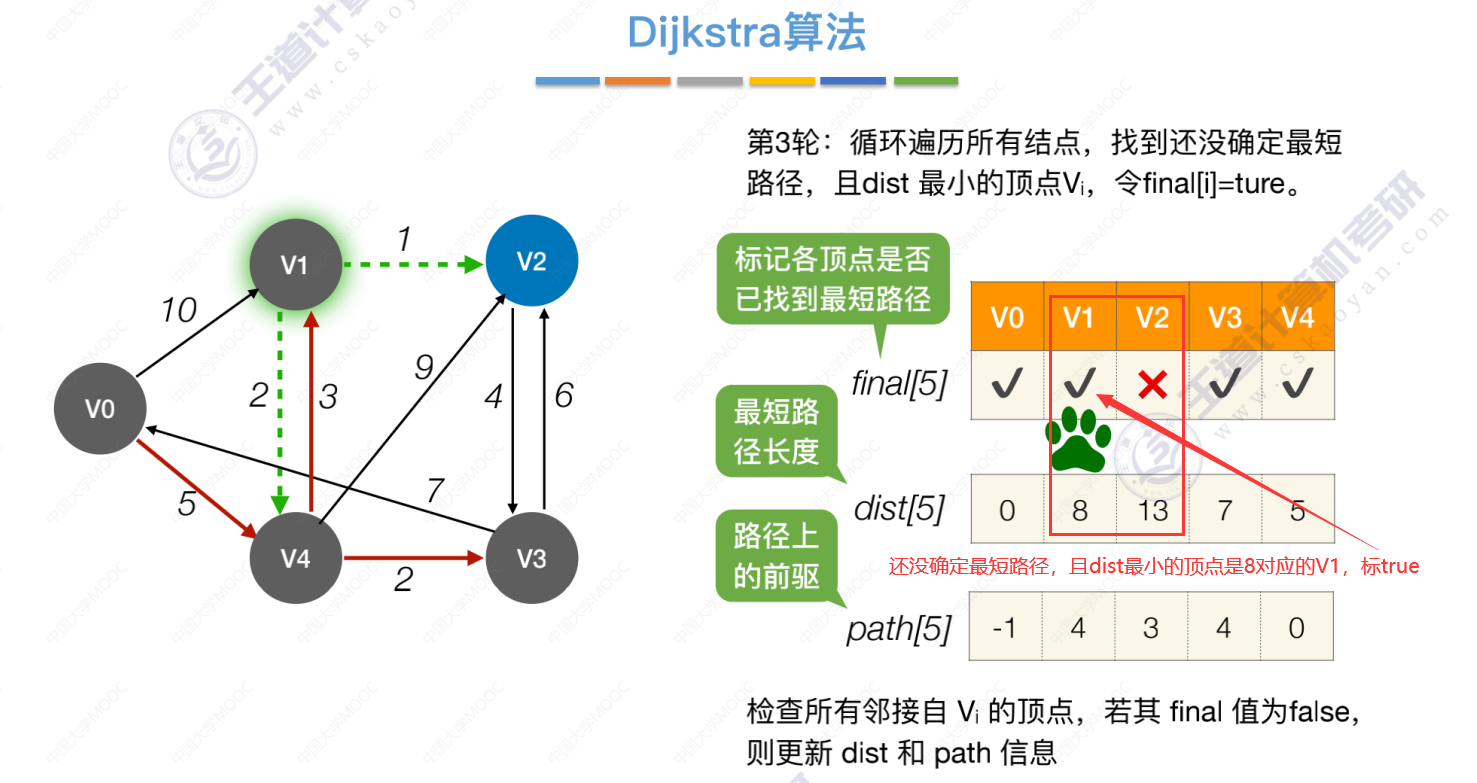
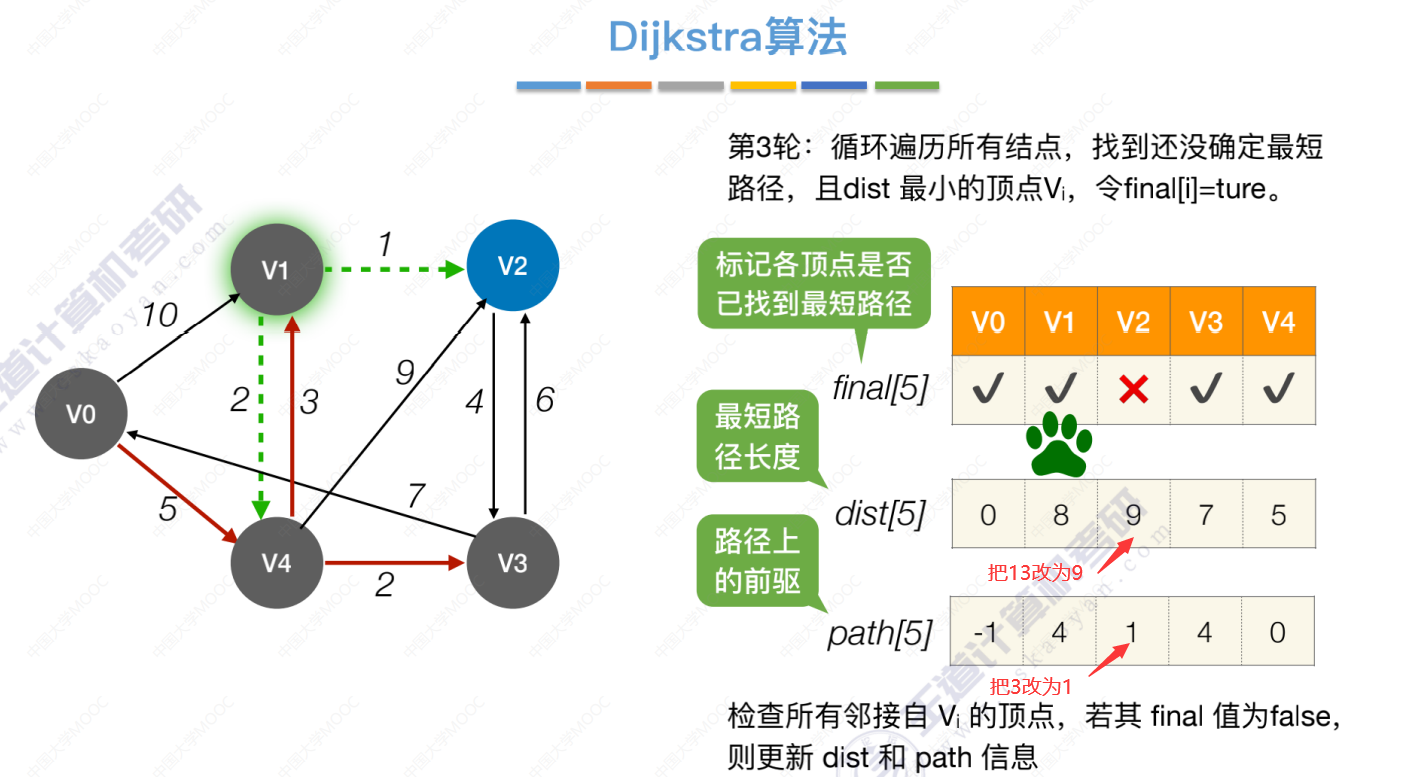
    在这里插入图片描述
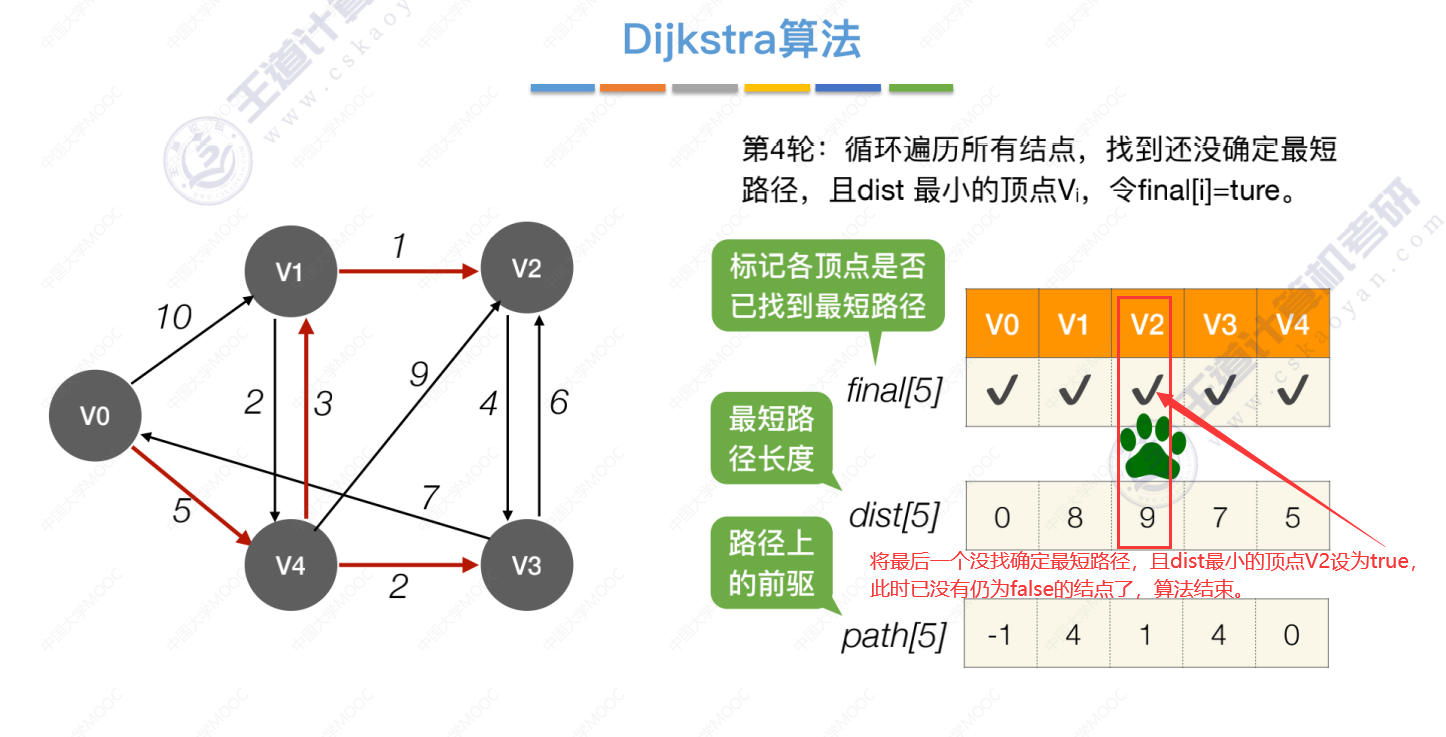
    在这里插入图片描述

    第2轮

    在这里插入图片描述
    在这里插入图片描述

    第3轮

    在这里插入图片描述
    在这里插入图片描述

    第4轮

    在这里插入图片描述

    如何使用数组信息？

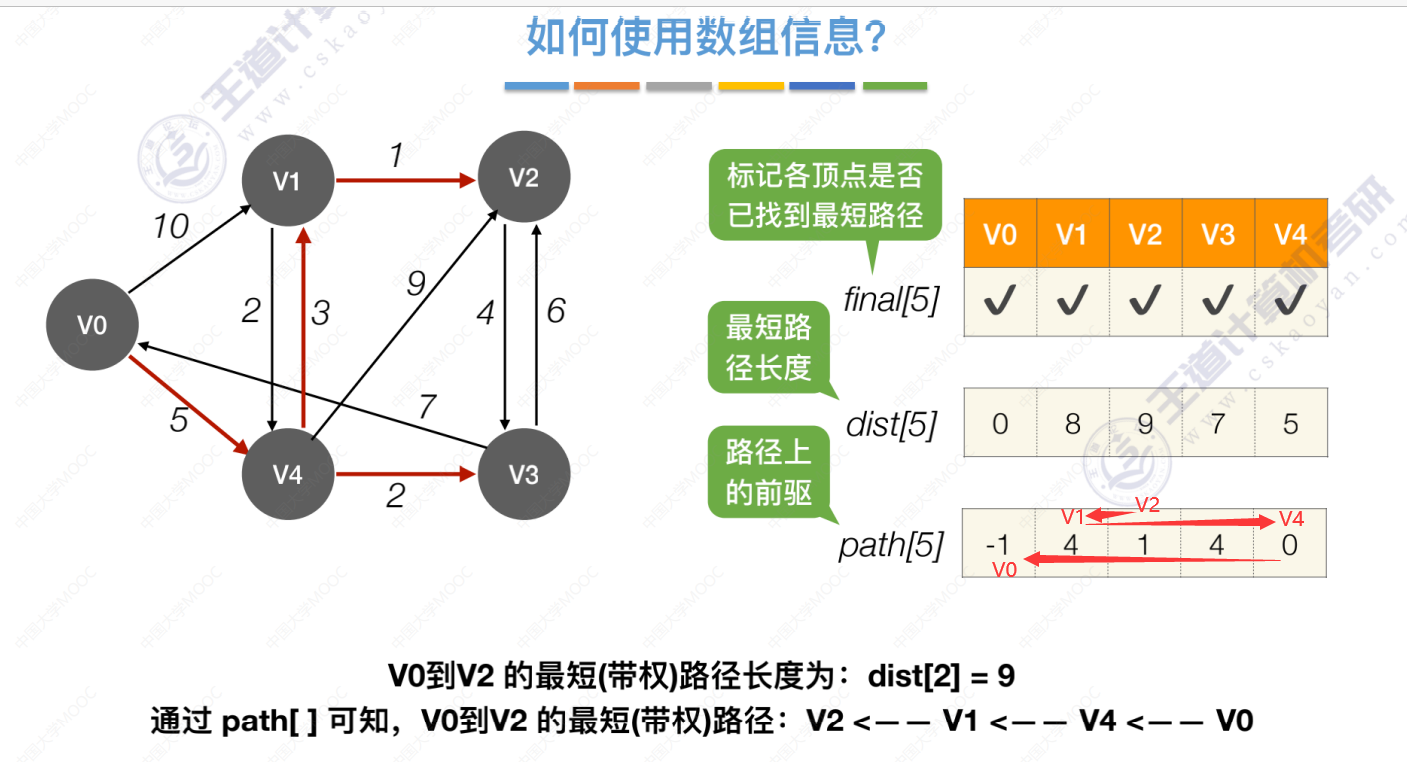
    在这里插入图片描述

    算法的时间复杂度

    每轮处理一个结点，（ 花费时间O(n) ）
    每处理一个结点要遍历一遍dist数组查找最小的。（ 花费时间O(n) ）
    时间复杂度 O(n²)
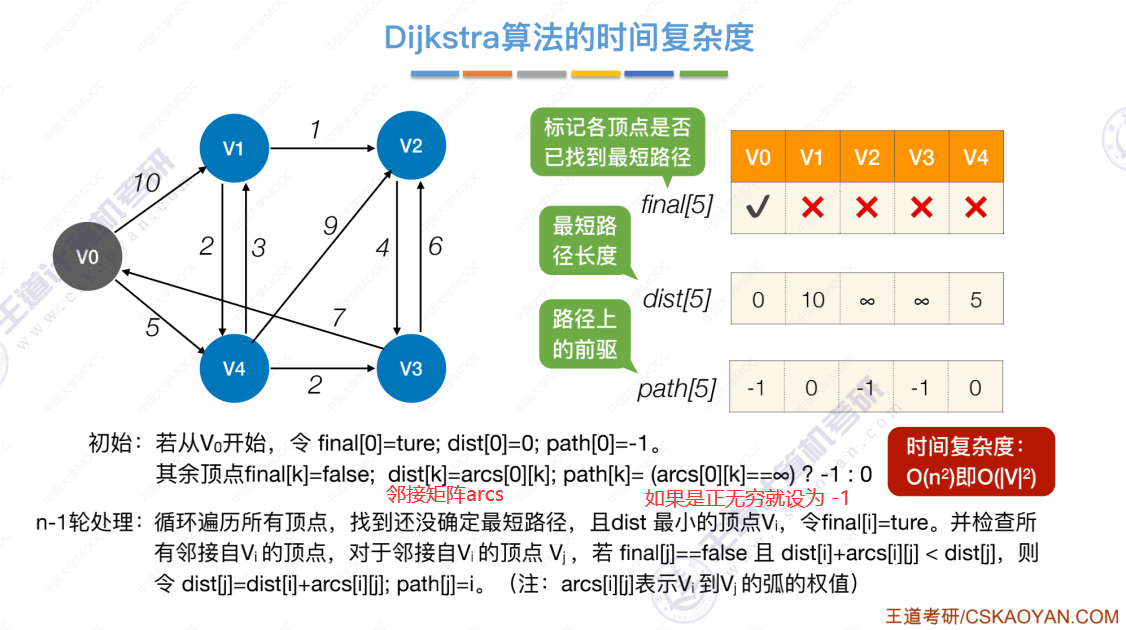
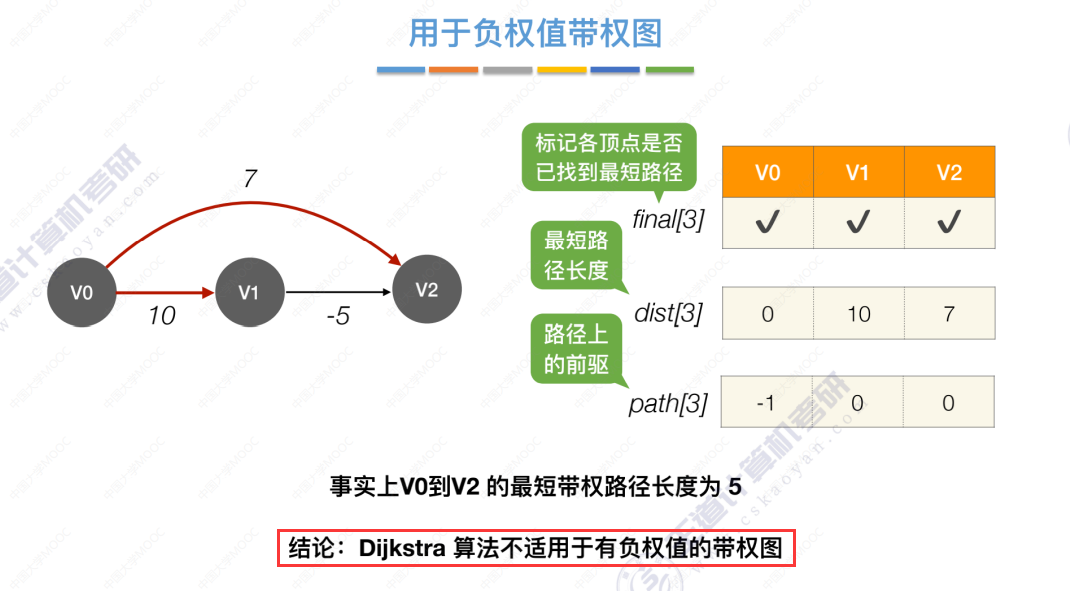
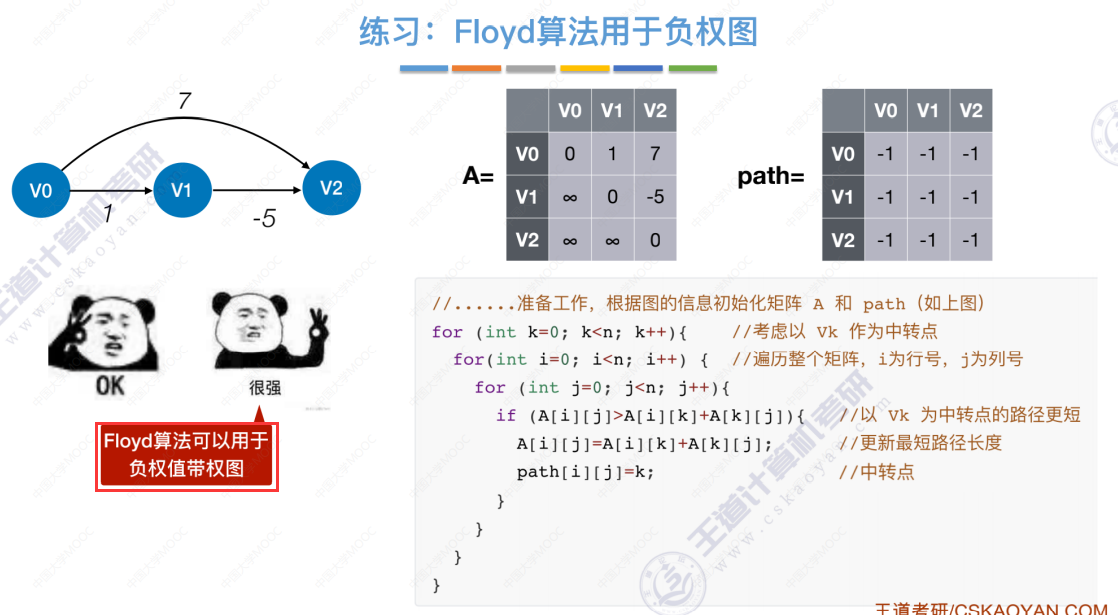
    在这里插入图片描述

    用于负权值带权图

    首先选择还没确定最短路径的，且dist中最小的值 的 对应顶点设为true。
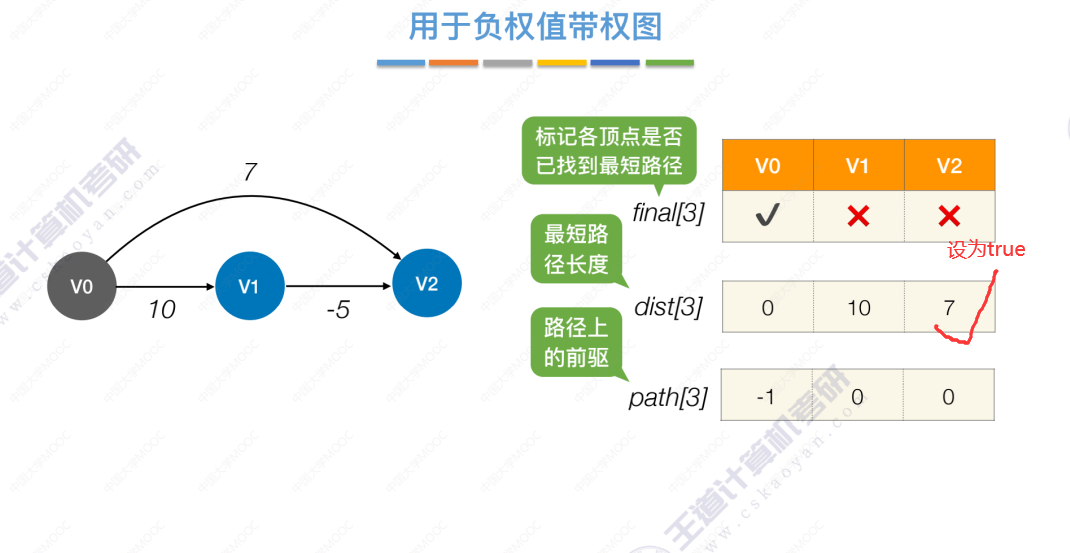
    在这里插入图片描述
    然后把V1设为true，算法结束。
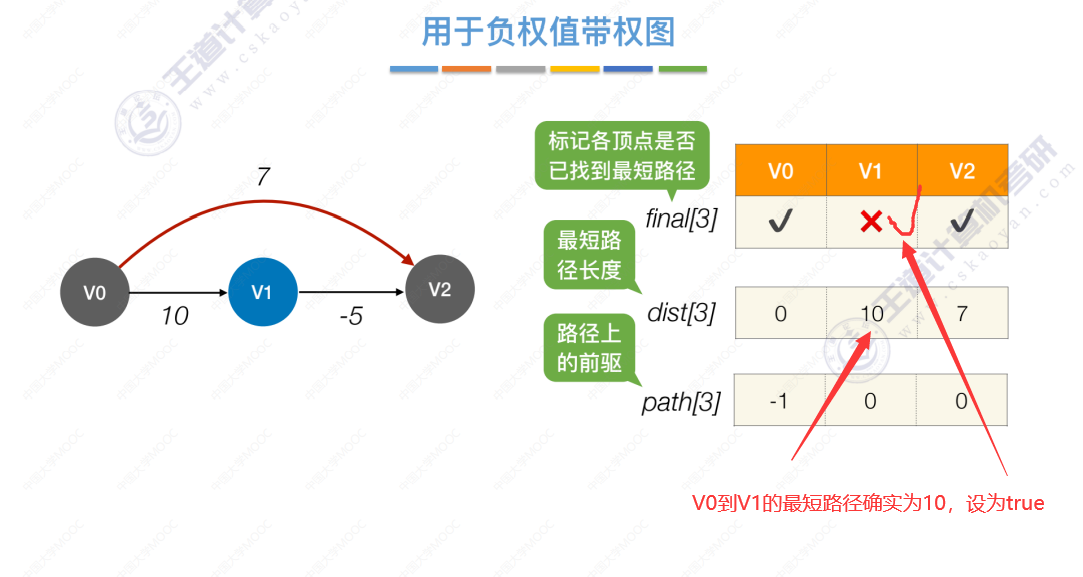
    在这里插入图片描述
    通过算法得出的V1到V2的最短路径是7，而实际最短路径是5，说明Dijkstra算法不适用于有负权值的带权图。
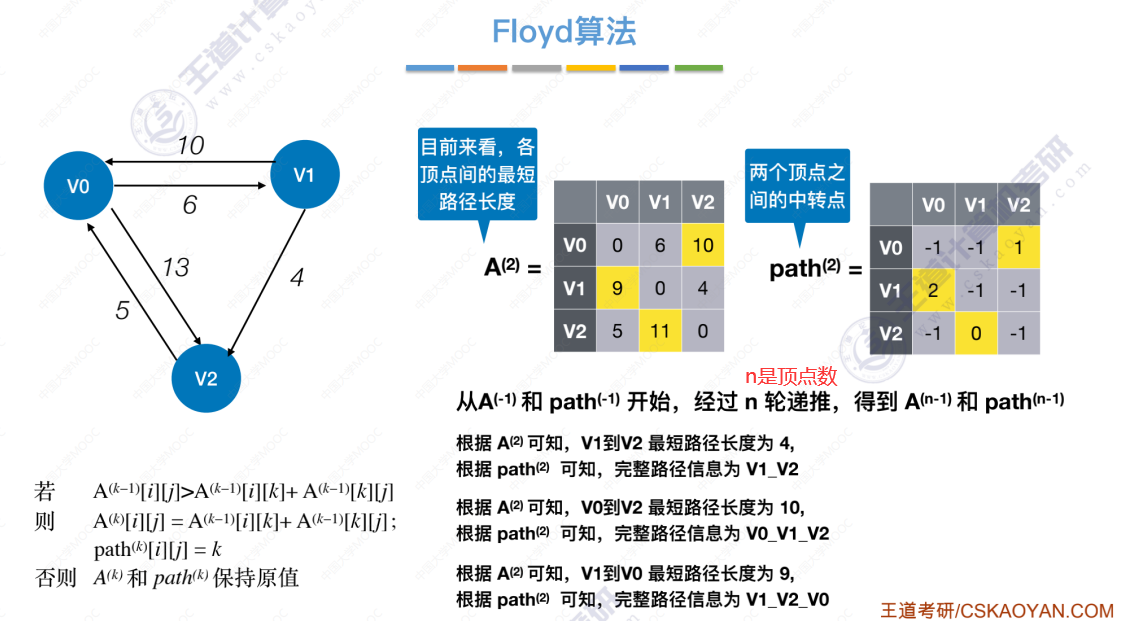
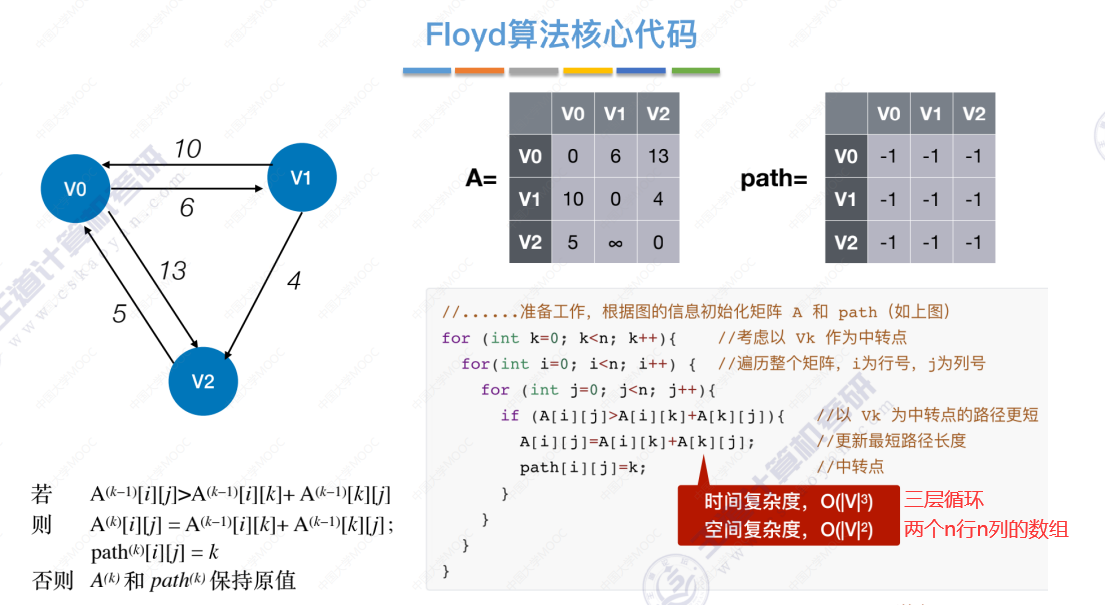
    在这里插入图片描述

    6.4-4 最短路径问题_Floyd算法（弗洛伊德算法）

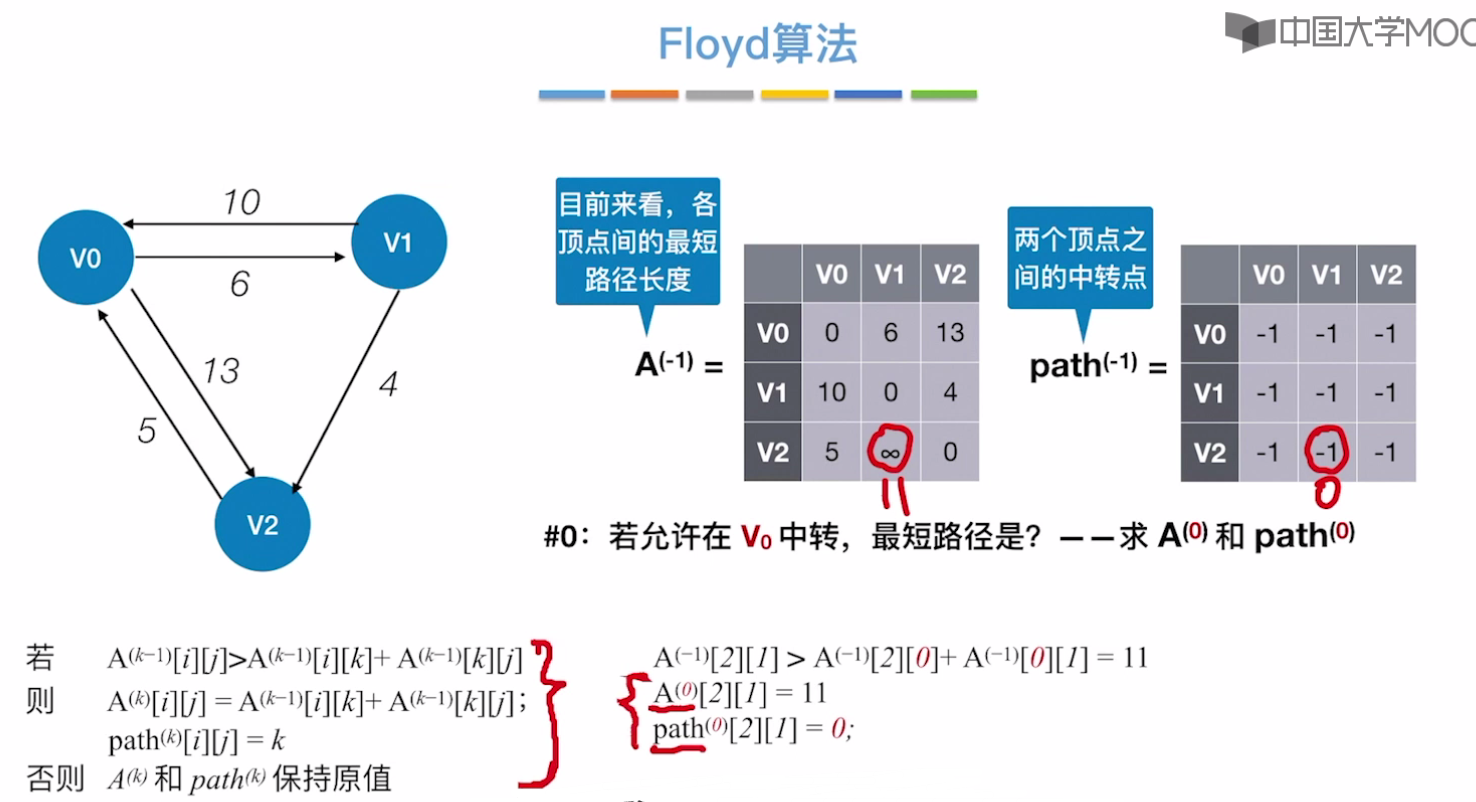
    在这里插入图片描述

    3个结点的弗洛伊德算法 演示

    允许V0中转后，仅会更新以下一处数据。
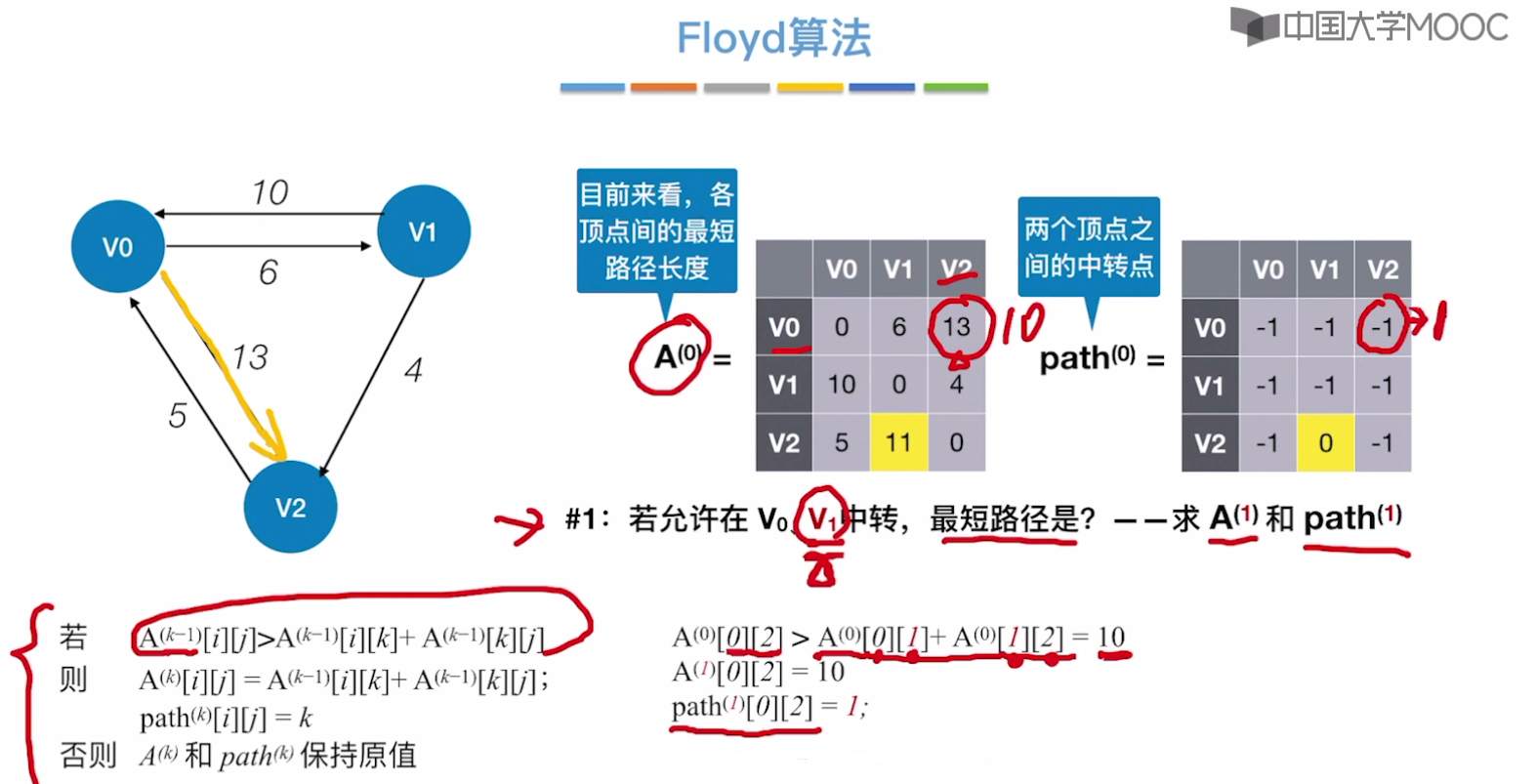
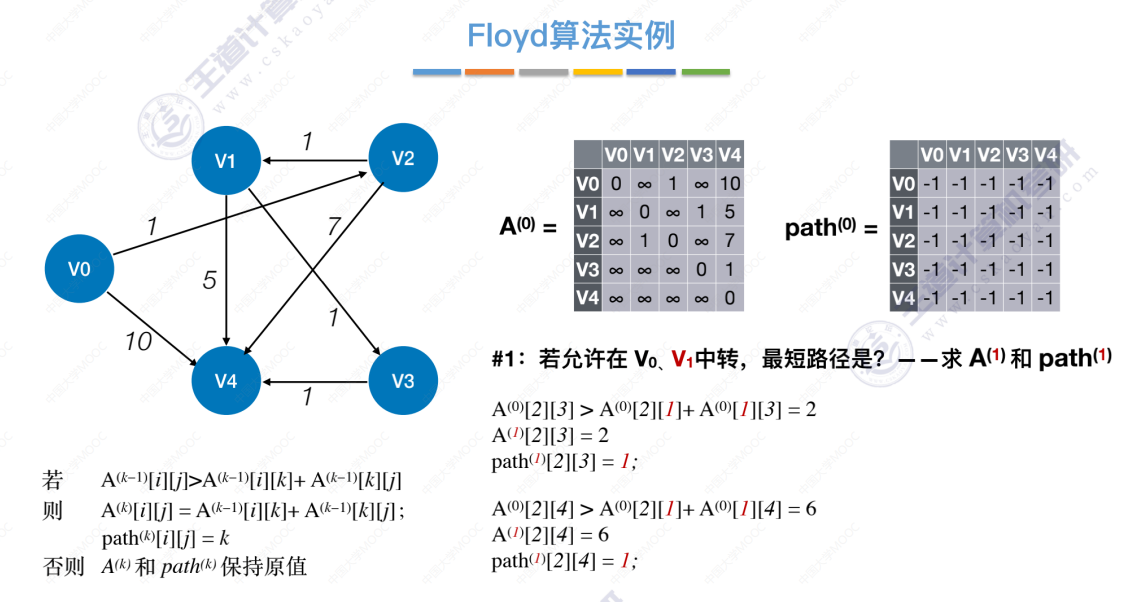
    在这里插入图片描述
    允许V0、V1中转后，仅会更新以下一处数据。
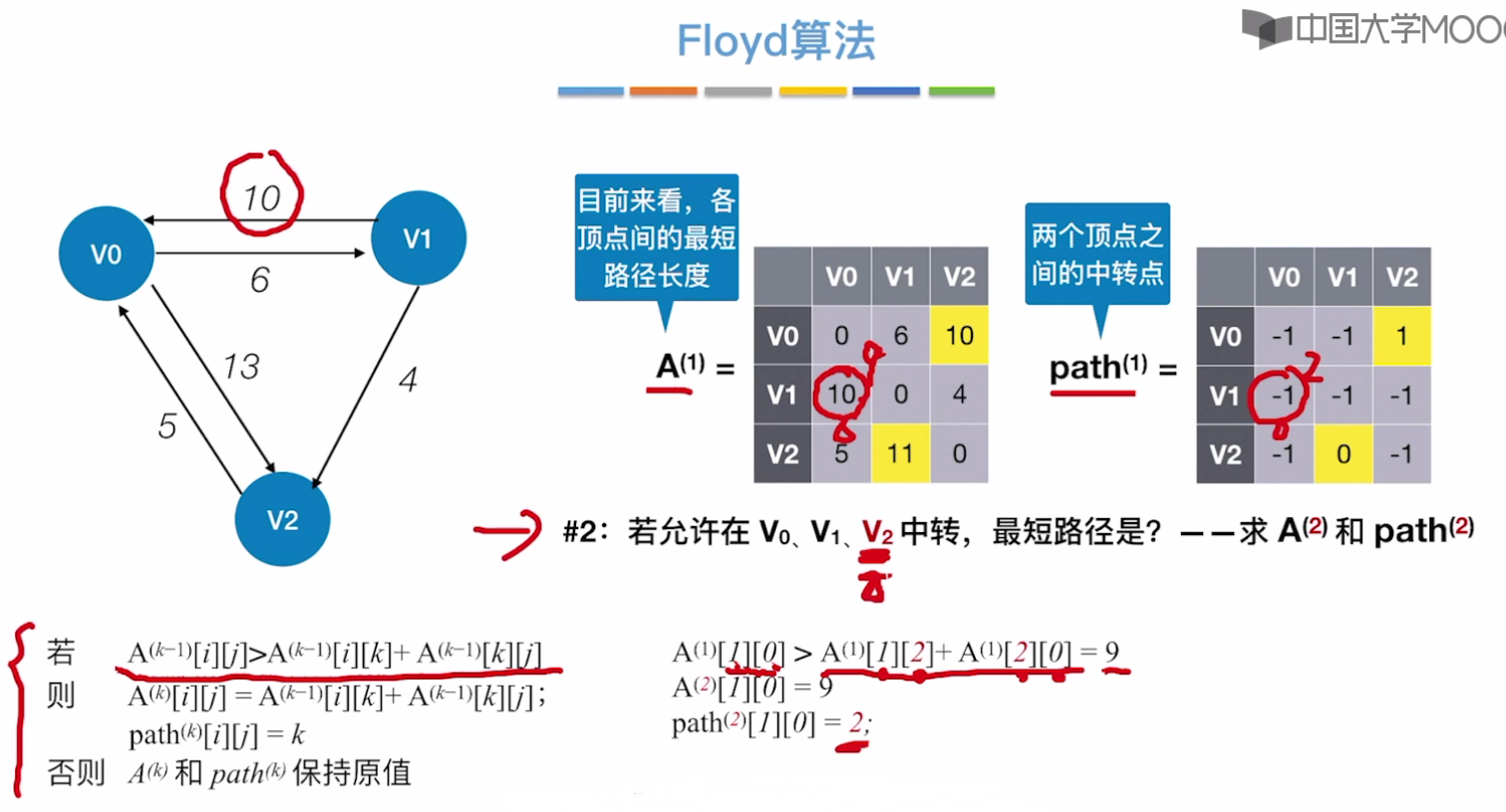
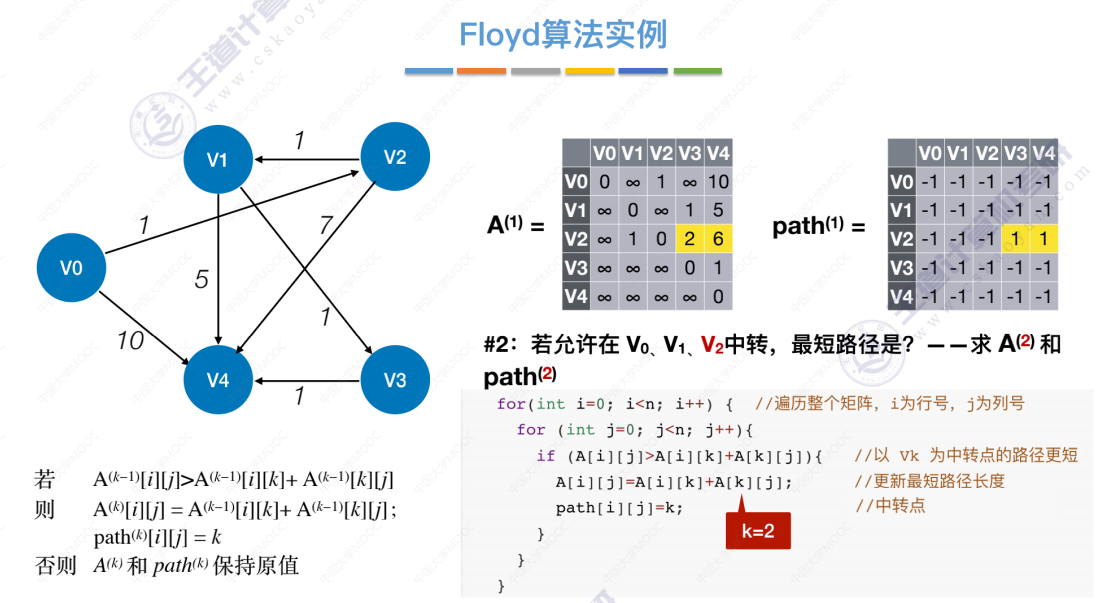
    在这里插入图片描述
    允许V0、V1、V2中转后，仅会更新以下一处数据。
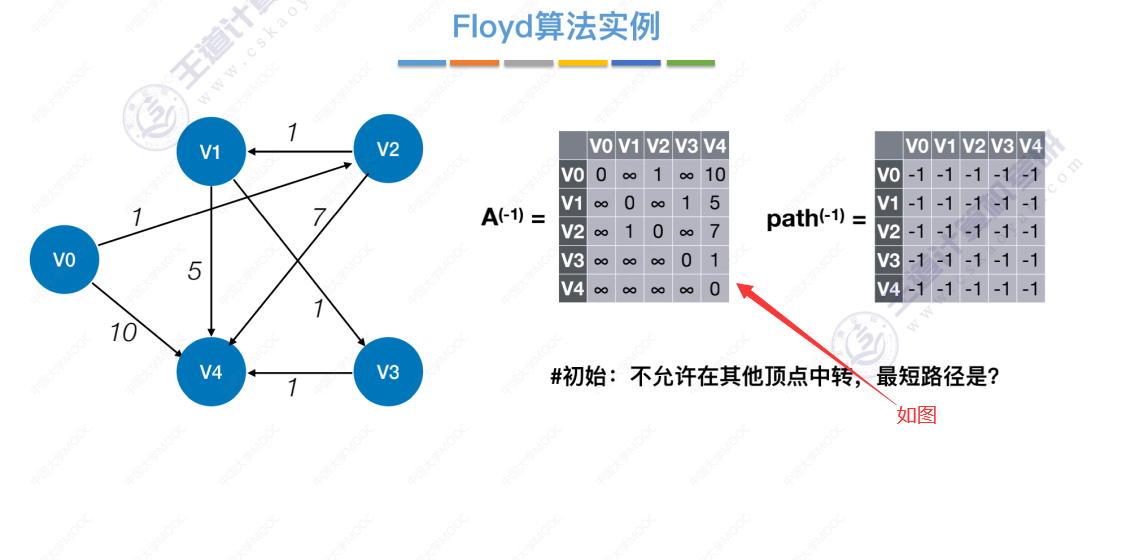
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述

    大于3个结点的弗洛伊德算法演示

    不允许中转点

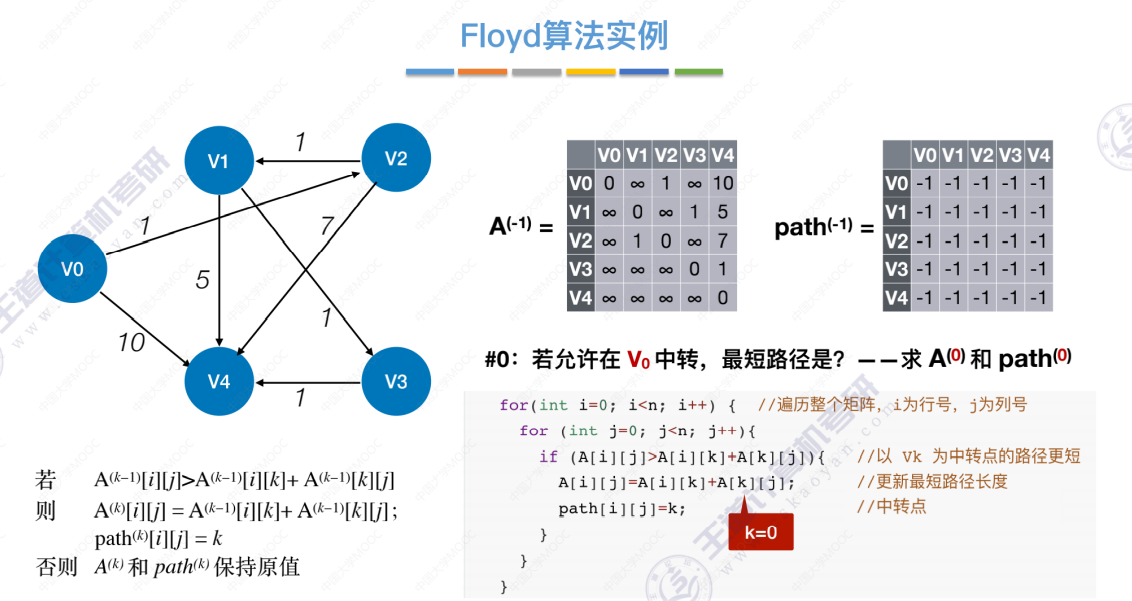
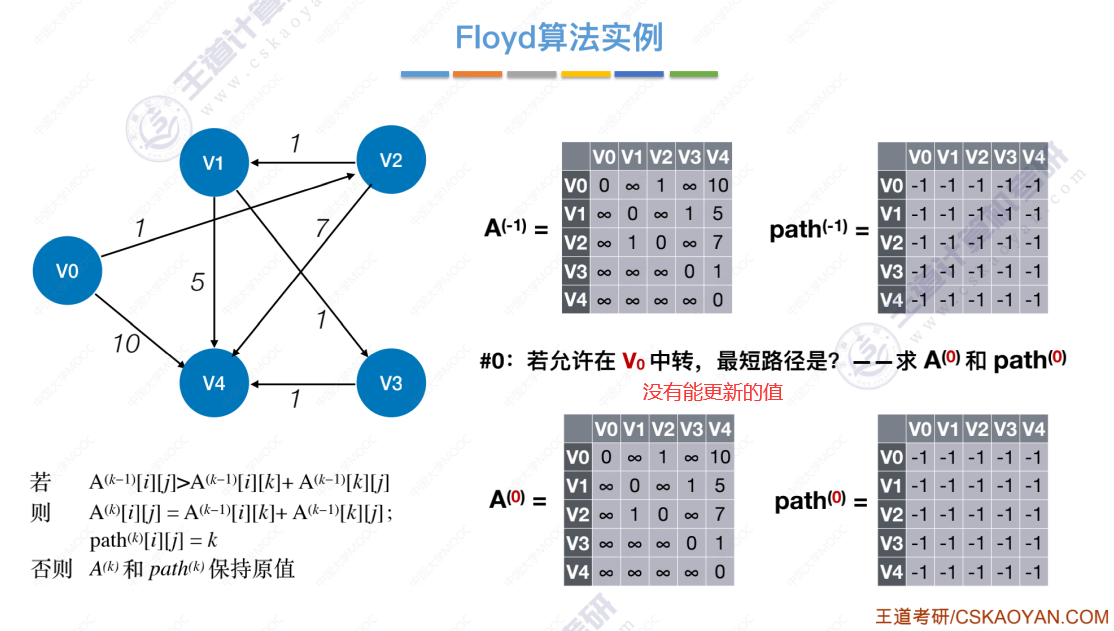
    在这里插入图片描述

    多目标最短路径模型及算法
    pdf 0星 超过10%的资源 314KB
    下载

    允许中转点V0

    在这里插入图片描述
    在这里插入图片描述

    允许中转点V0、V1

    在这里插入图片描述
    在这里插入图片描述

    允许中转点V0、V1、V2

    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述

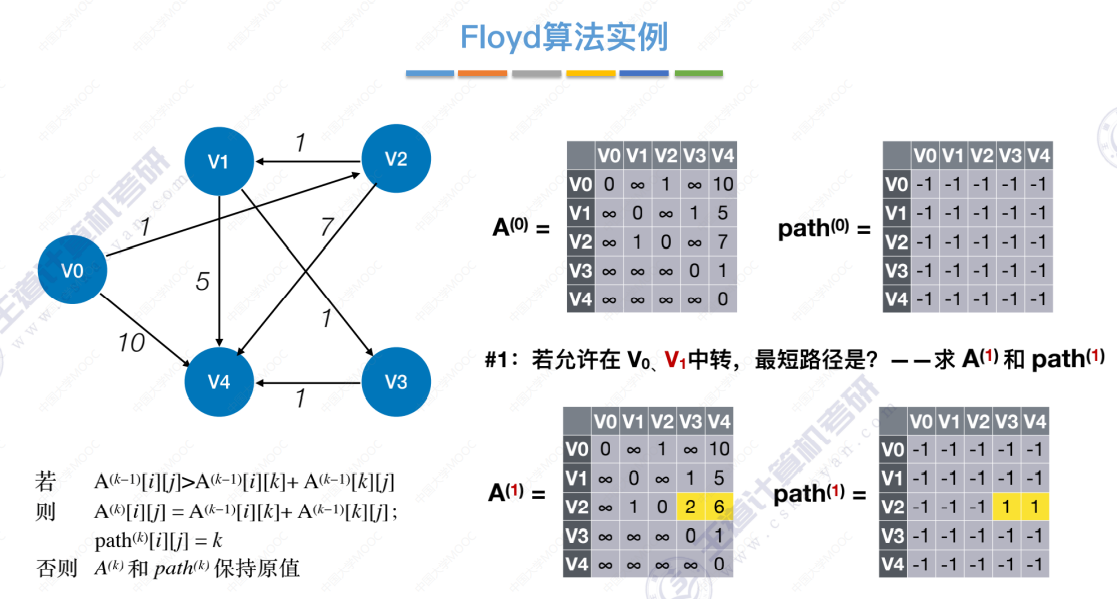
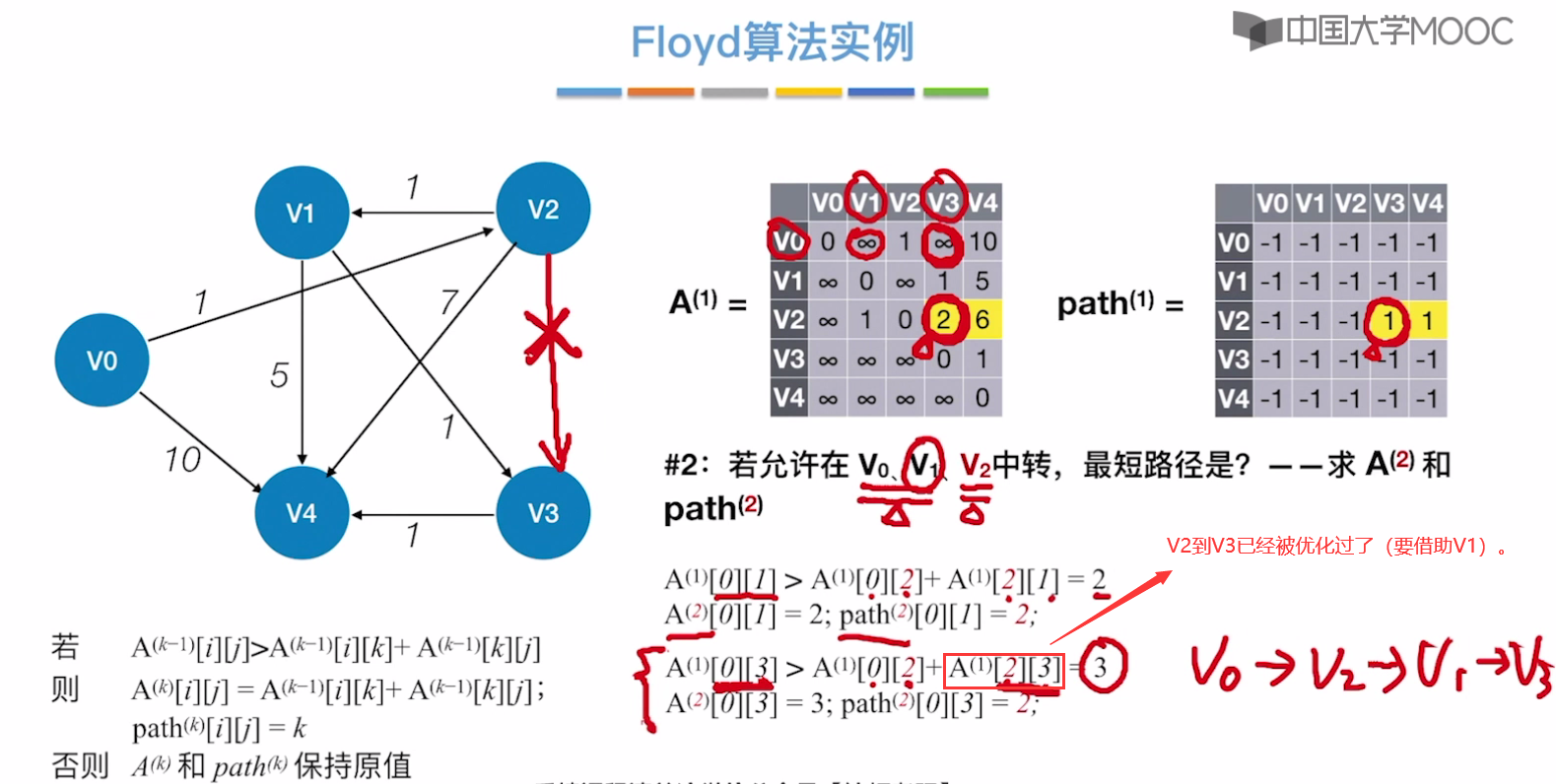
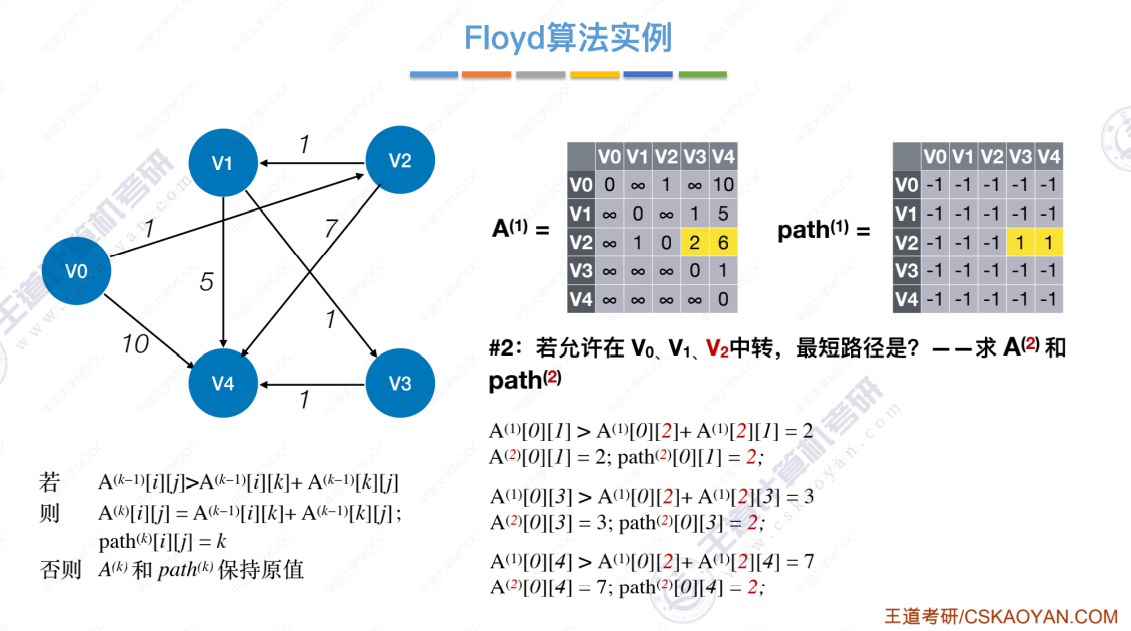
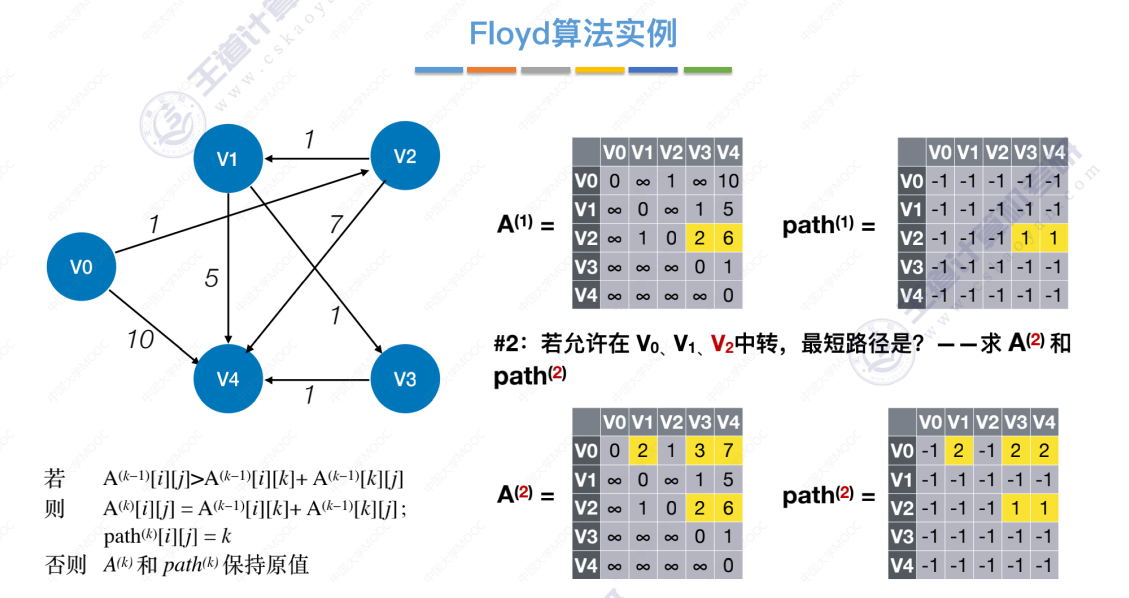
    允许中转点V0、V1、V2、V3

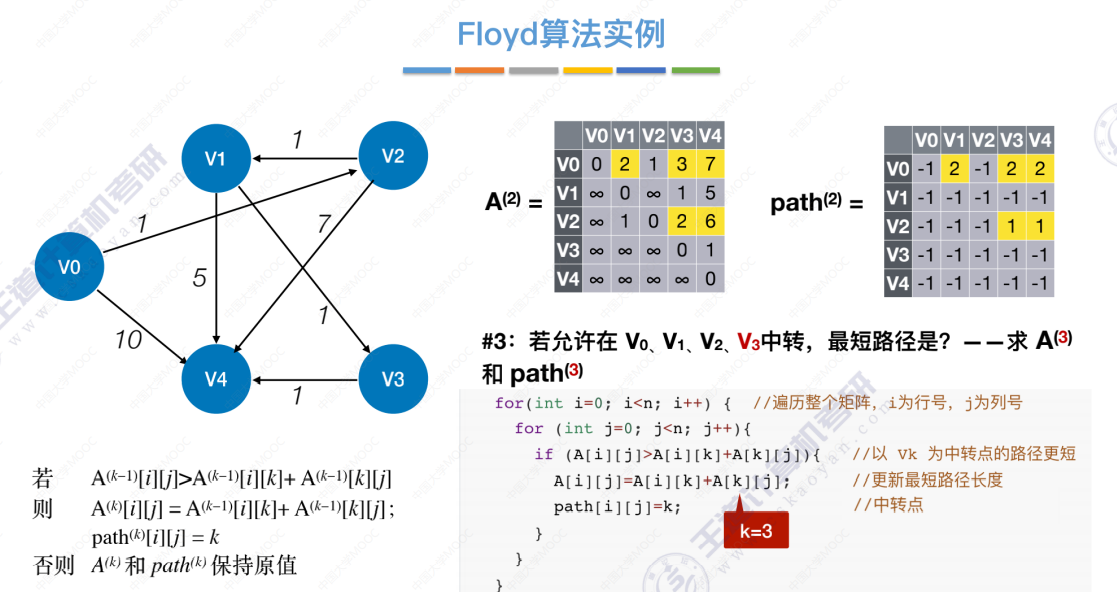
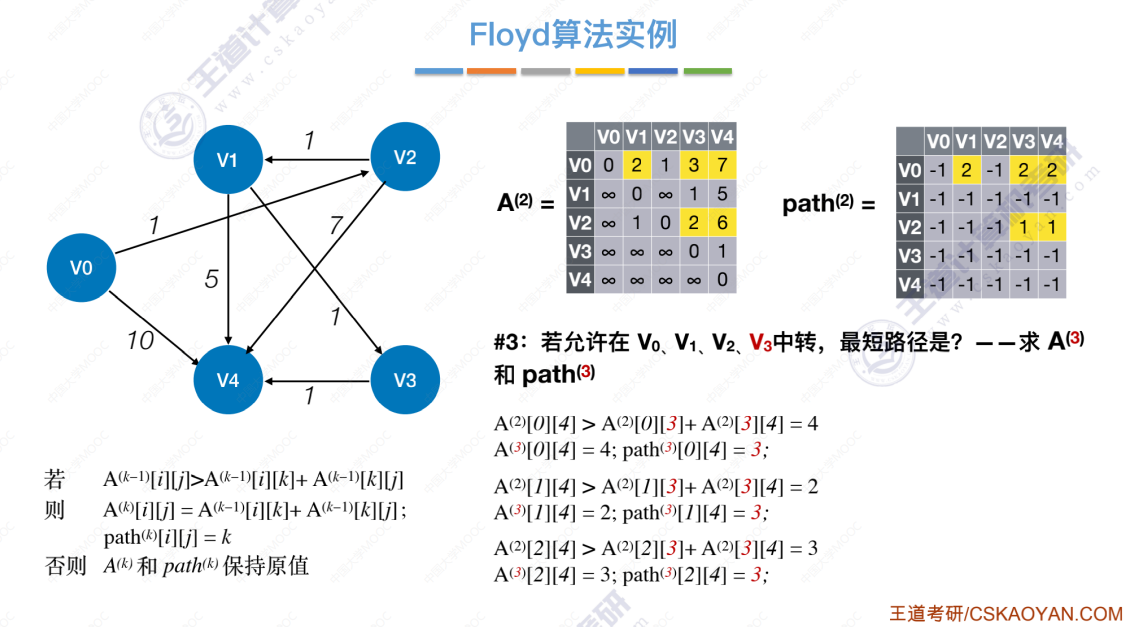
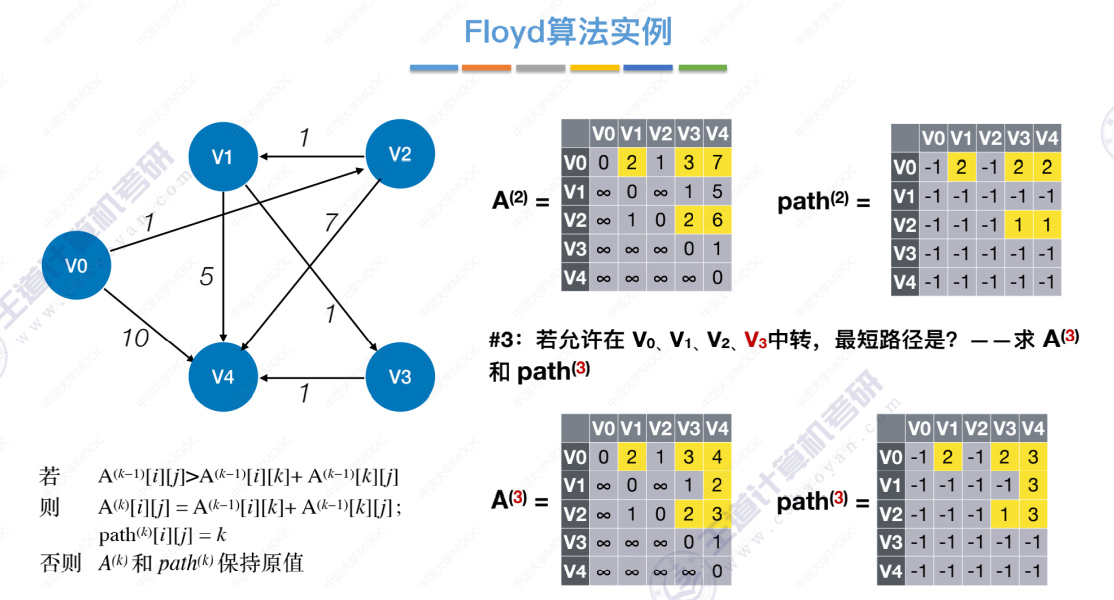
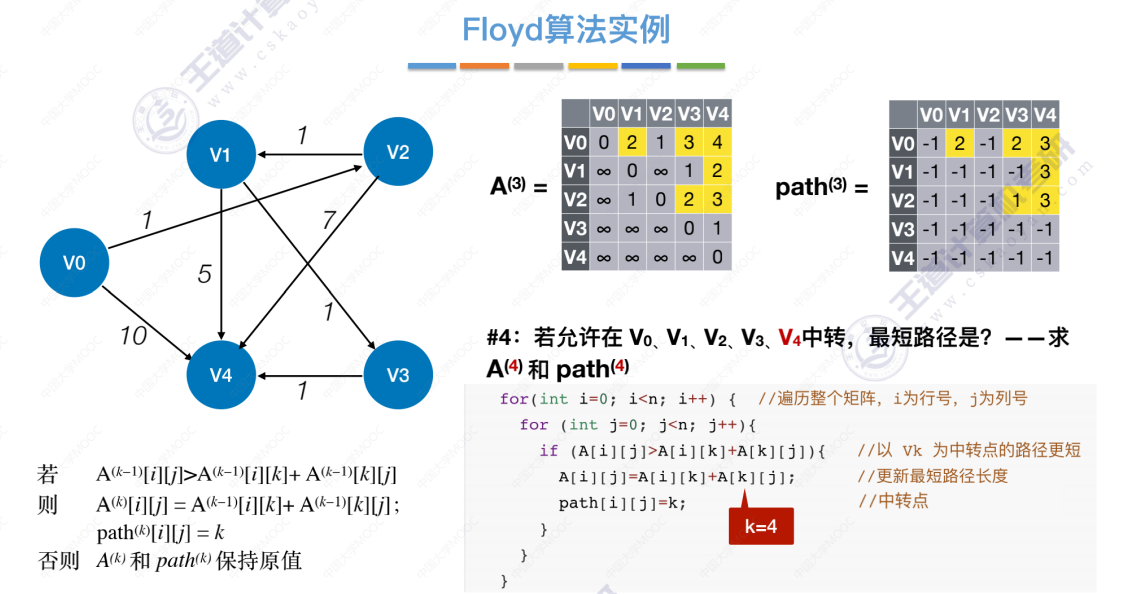
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述

    允许中转点V0、V1、V2、V3、V4

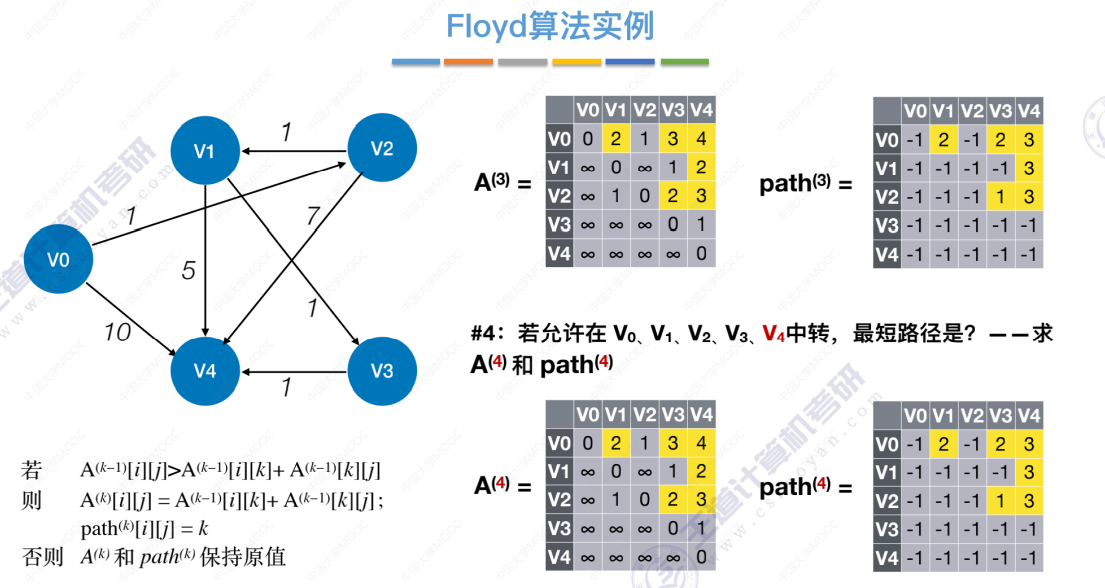
    在这里插入图片描述
    在这里插入图片描述

    使用数组信息（A、path）找出最短路径

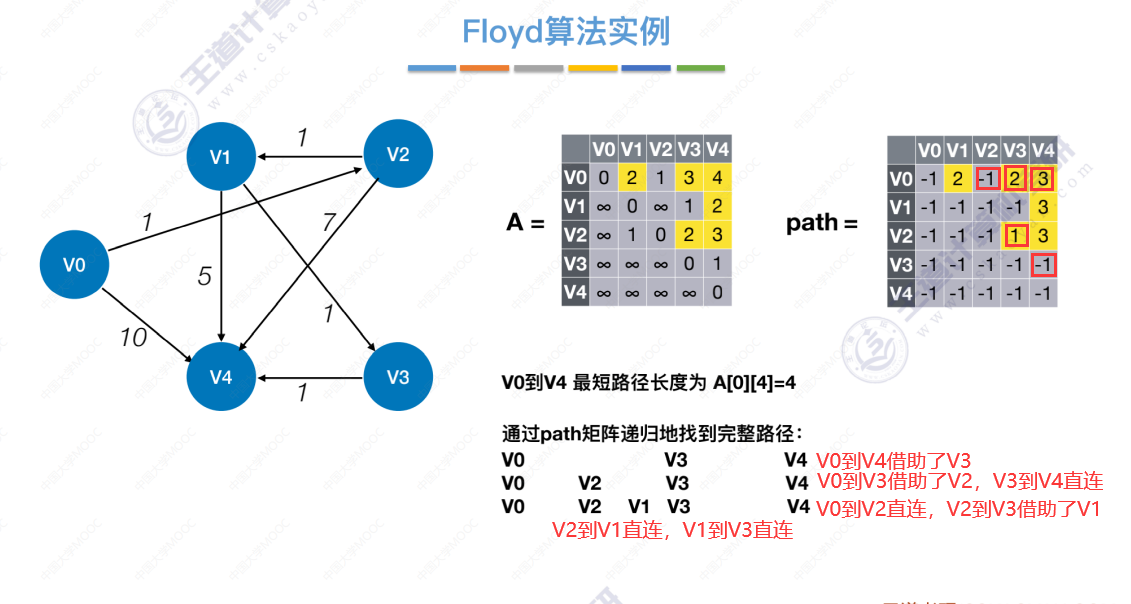
    在这里插入图片描述

    Floyd算法可以用于负权图

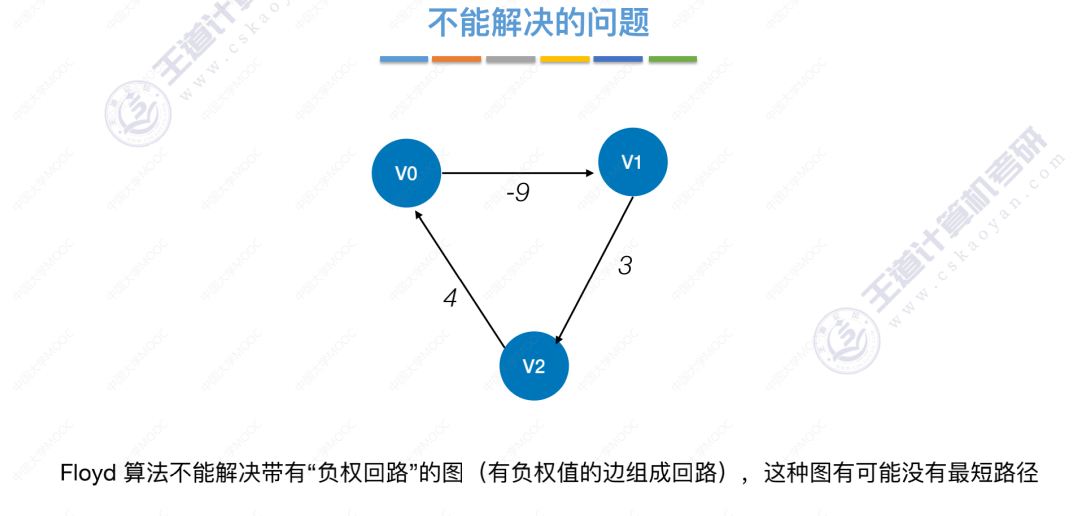
    在这里插入图片描述

    弗洛伊德算法不能解决的问题

    比如从V0走到V1是-9，
    如果V0->V1->V2->V0->V1是-9+(3+4±9)=-9±2=-11
    这样每走一圈，V0到V1的最短路径就更小一次，没有尽头，无穷无尽。
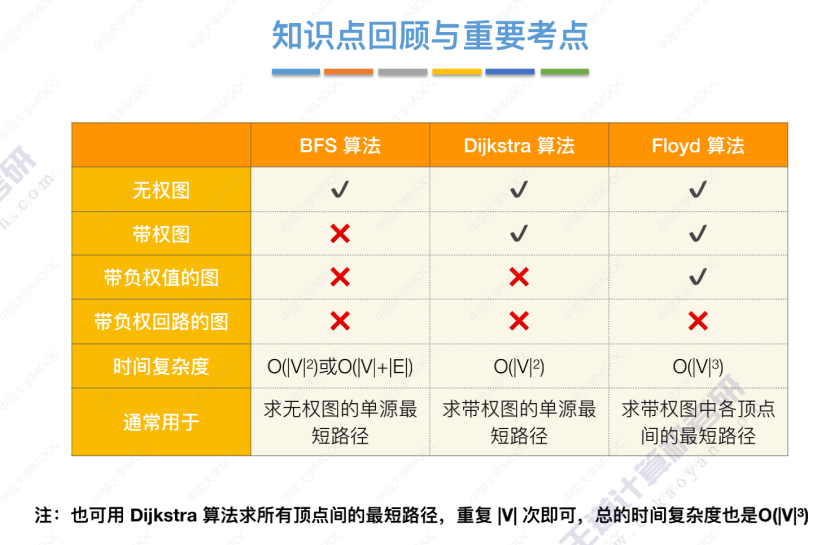
    在这里插入图片描述

    最小路径总结

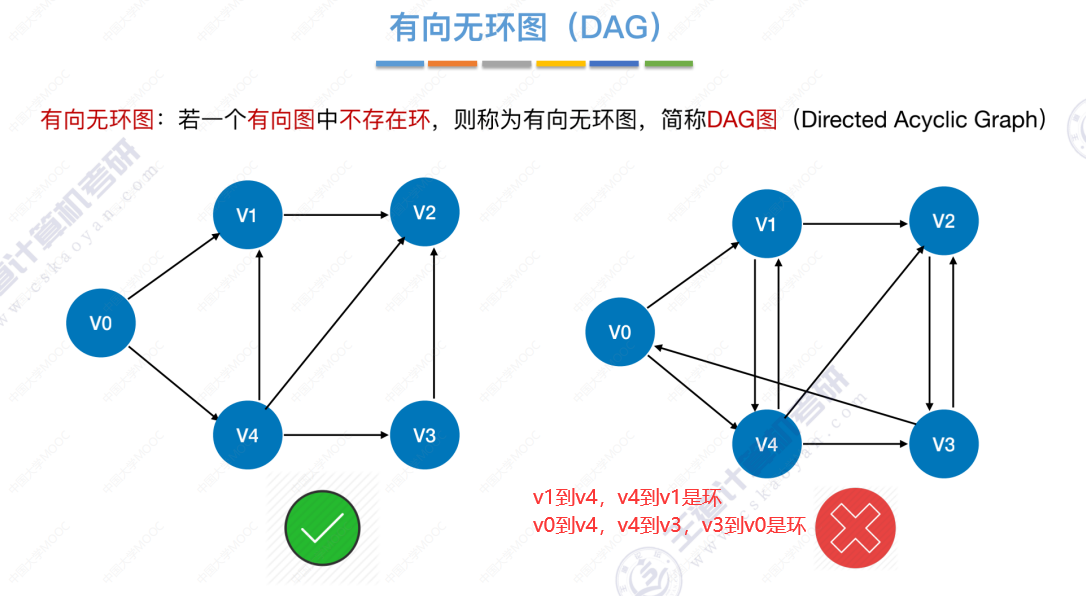
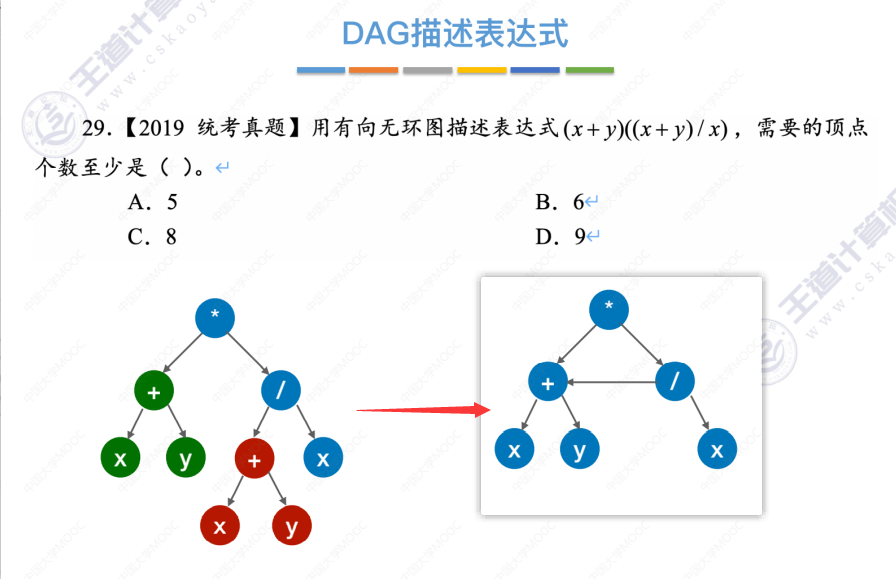
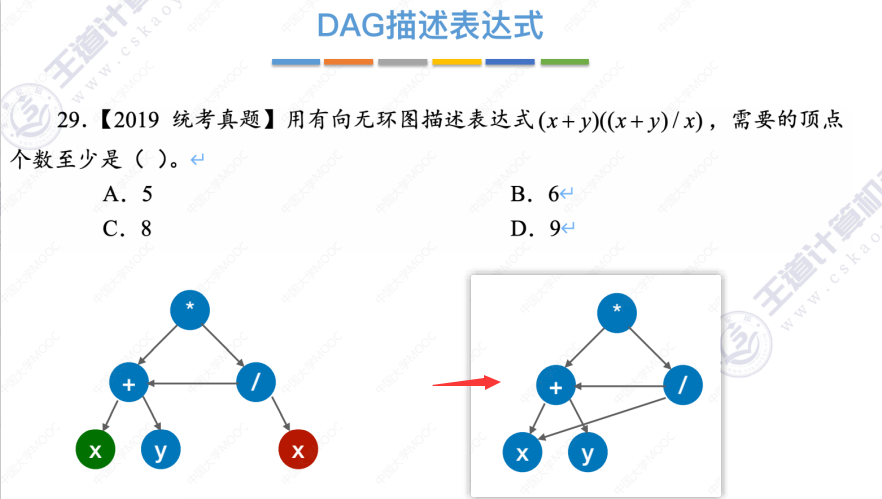
    在这里插入图片描述

    6.4-5 有向无环图描述表达式

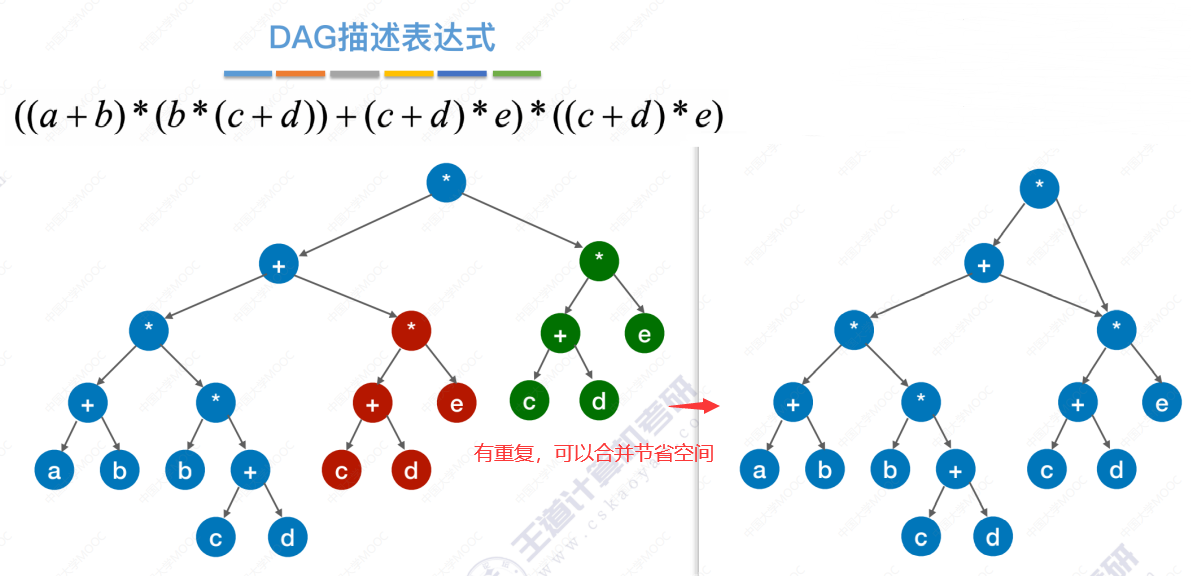
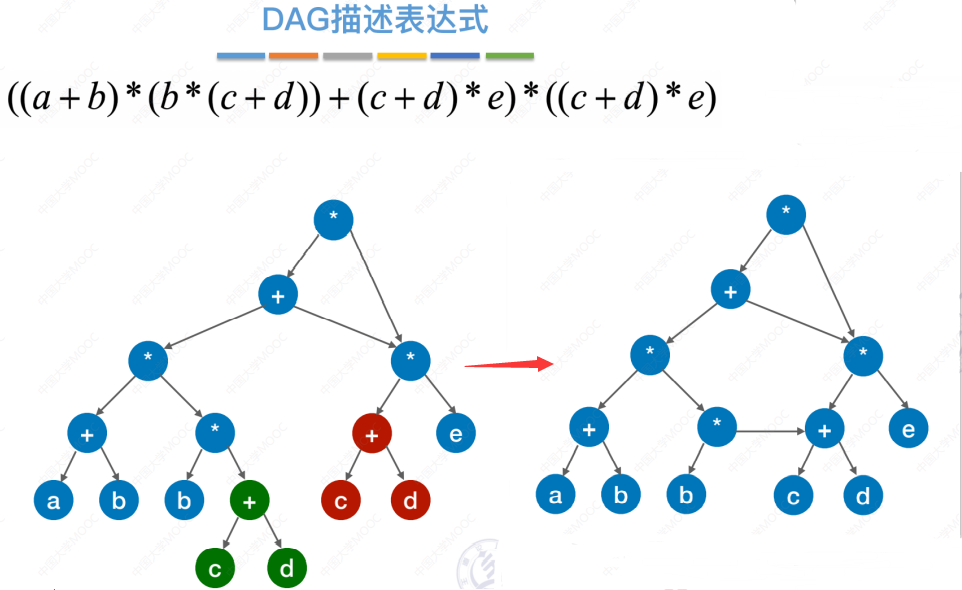
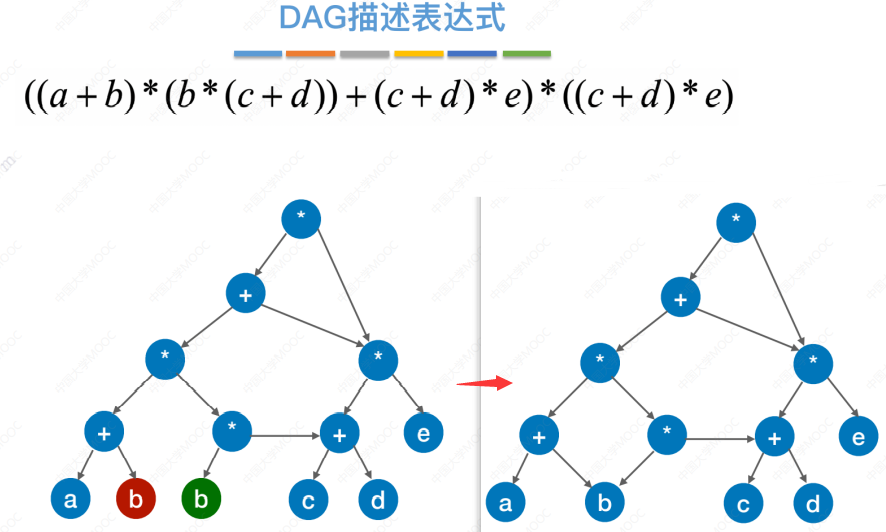
    在这里插入图片描述

    将一棵树简化成有向无环图的过程

    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述

    一道练习（答案是A.5）

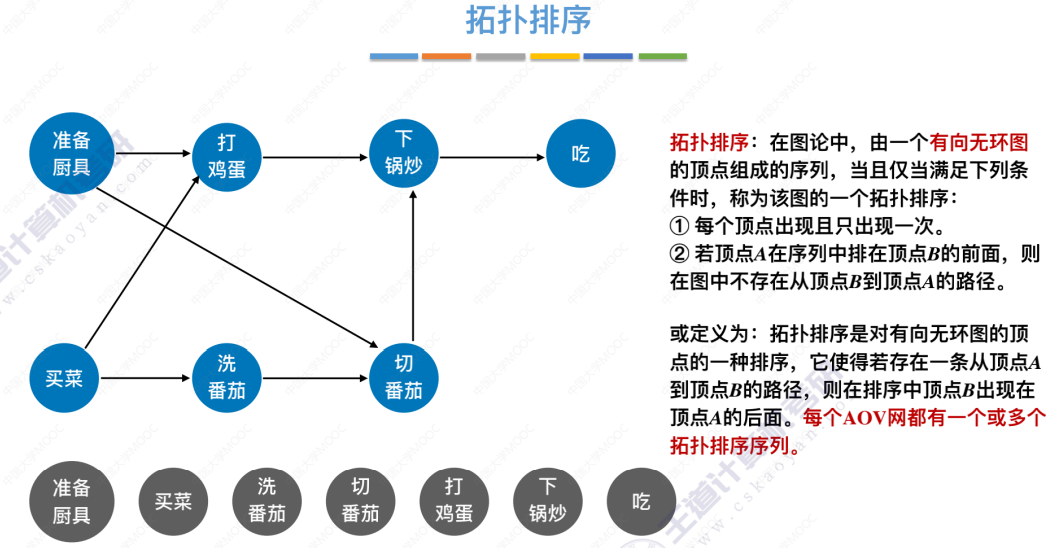
    在这里插入图片描述
    在这里插入图片描述

    6.4-6 拓扑排序

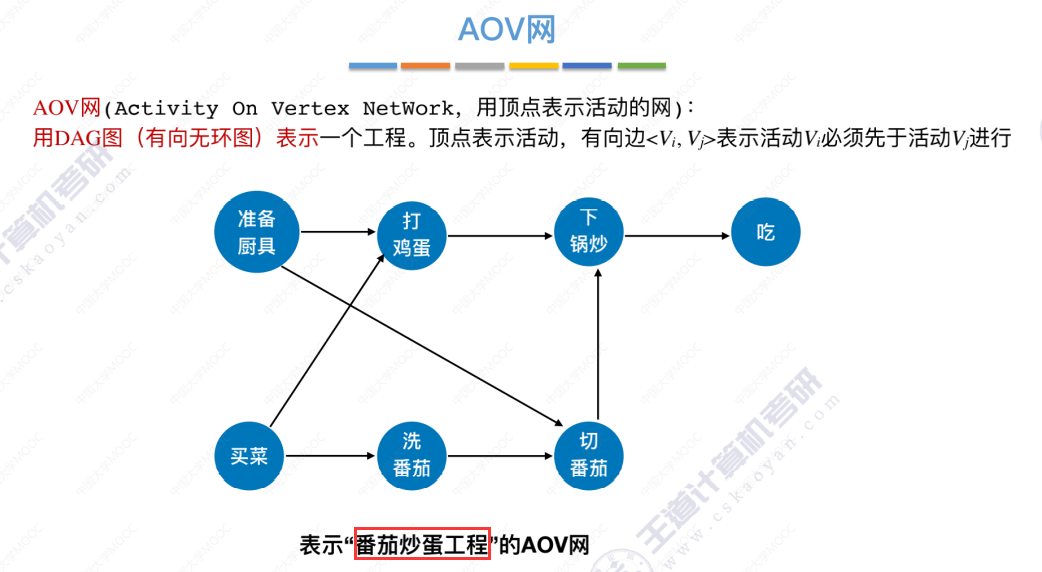
    AOV网

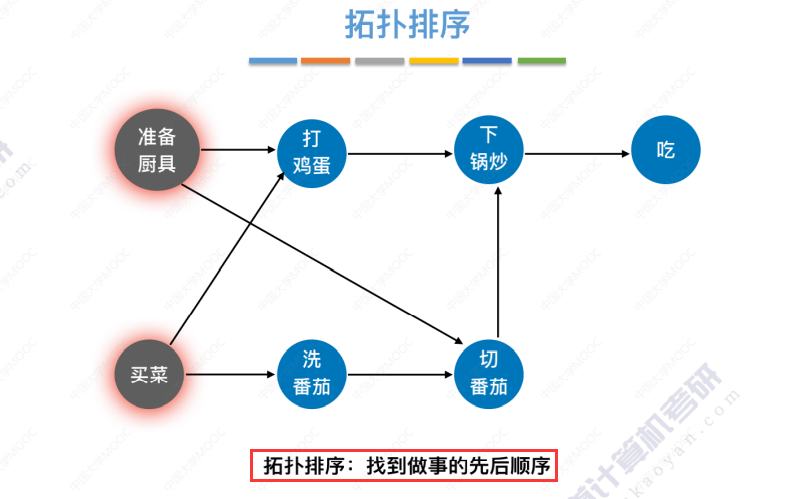
    在这里插入图片描述

    拓扑排序引入

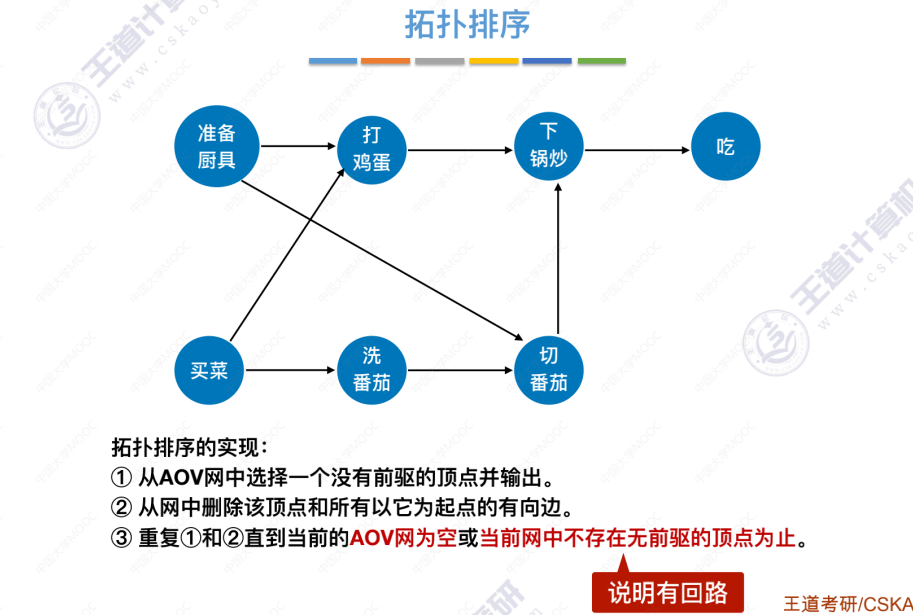
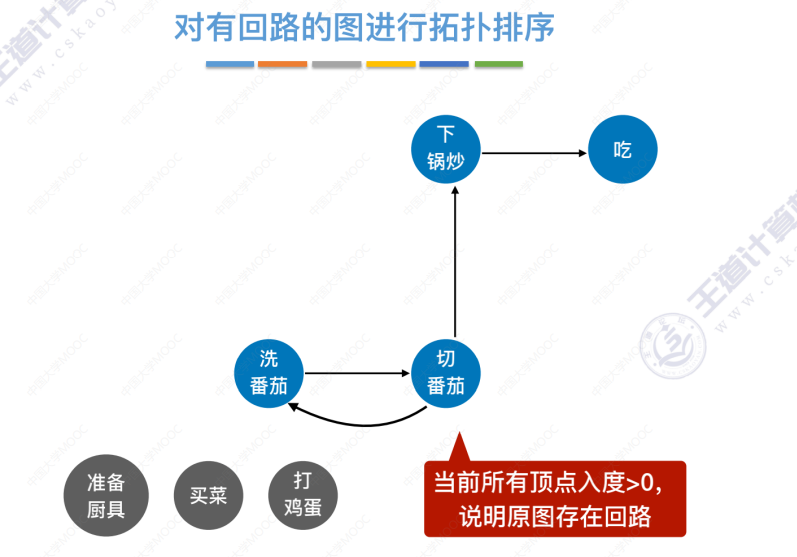
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述

    拓扑排序代码实现

    代码实现过程

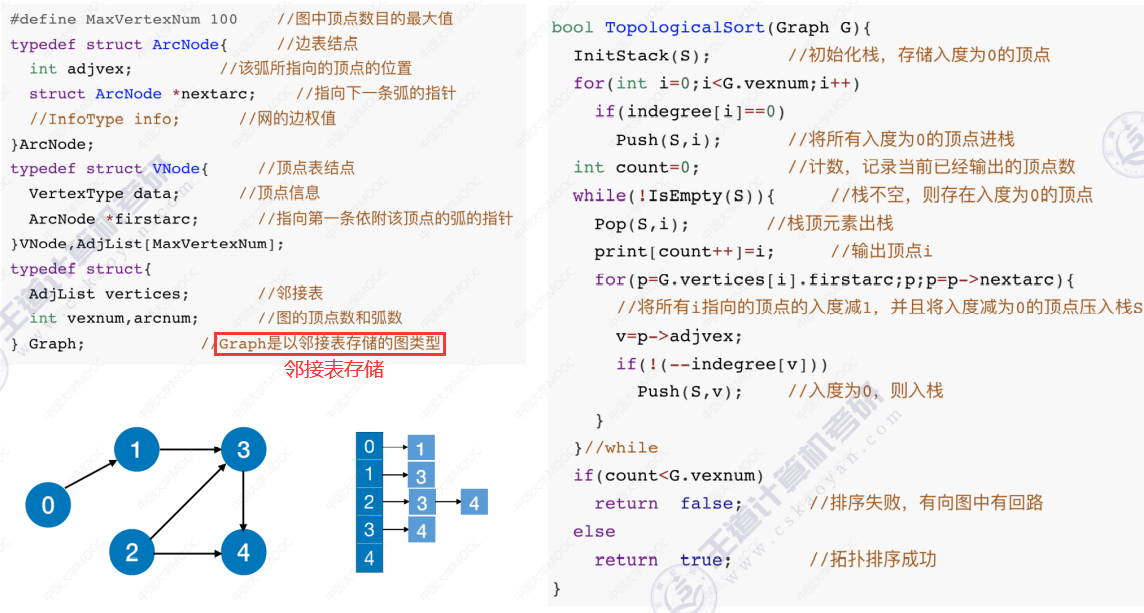
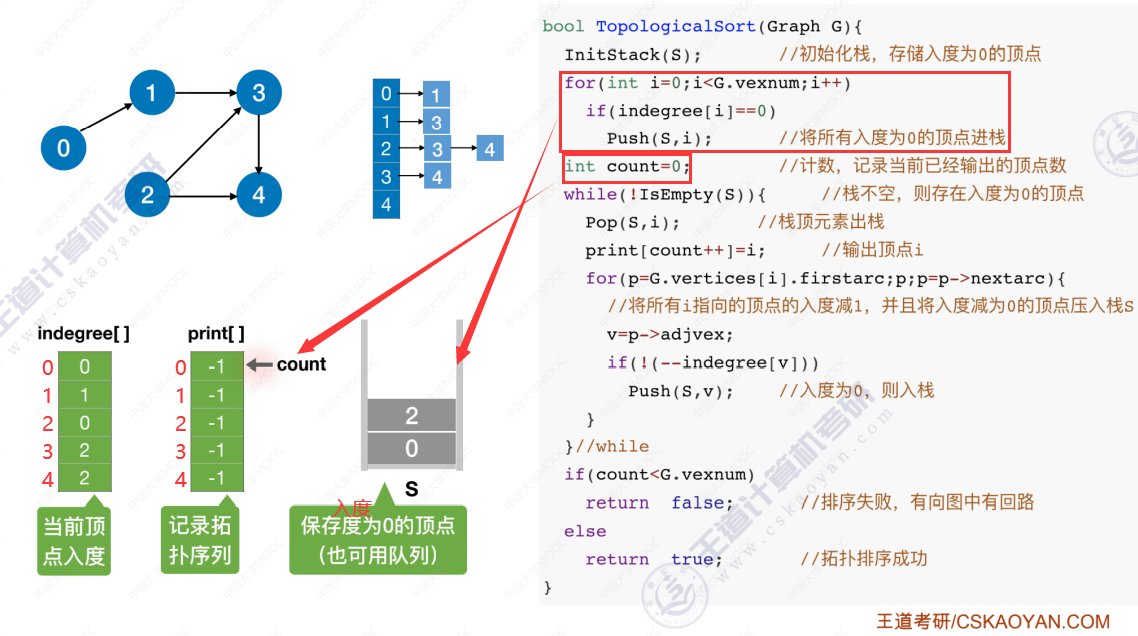
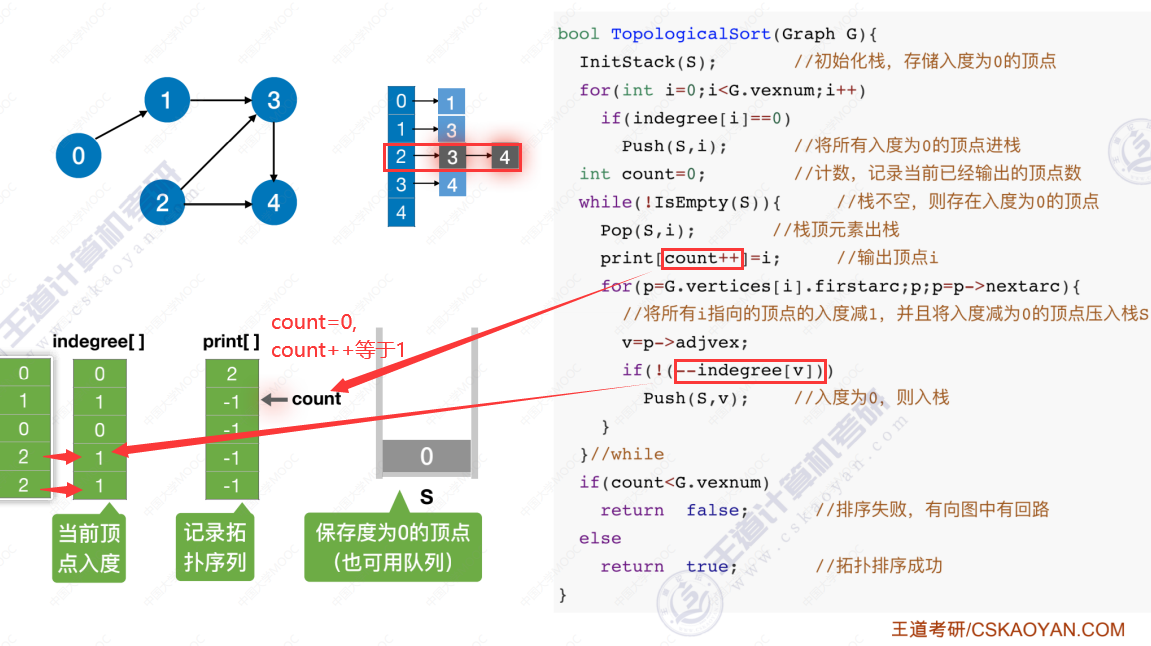
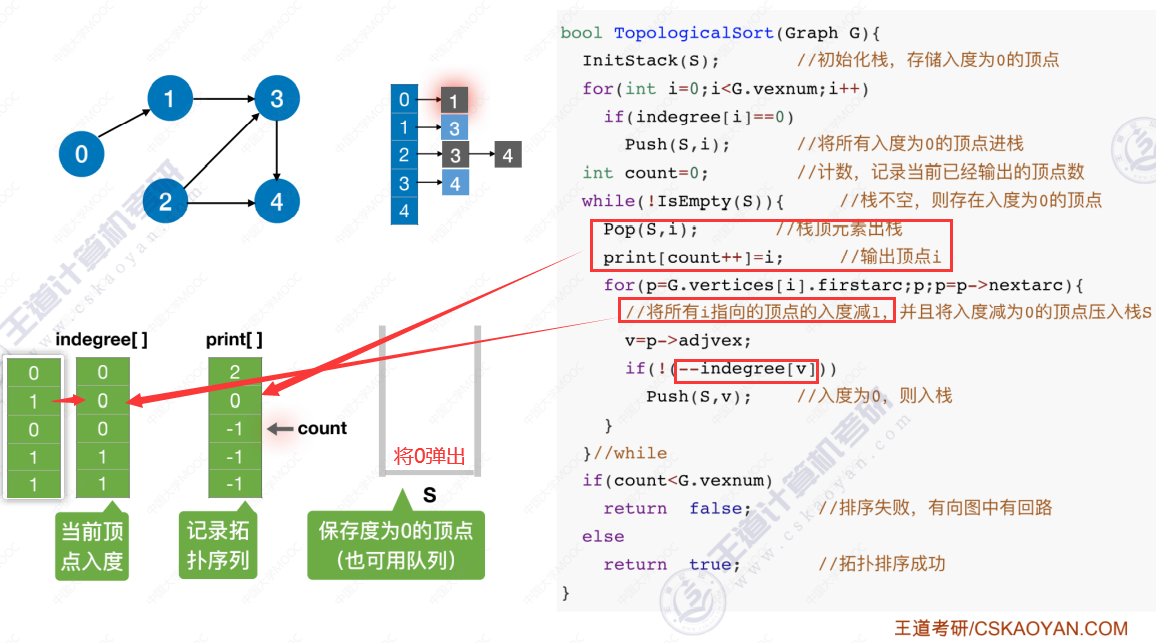
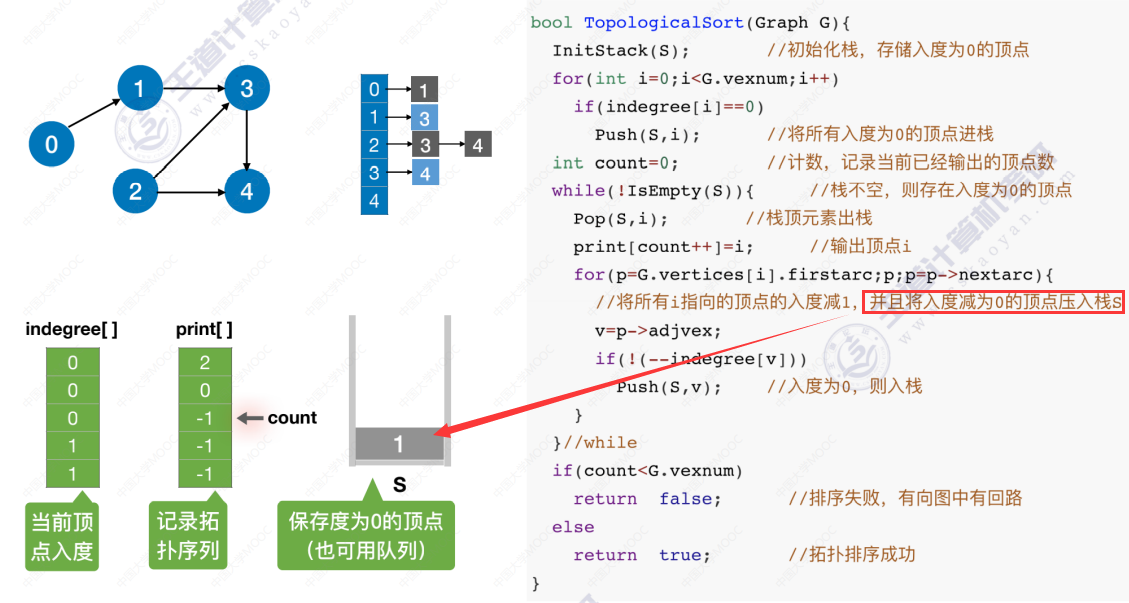
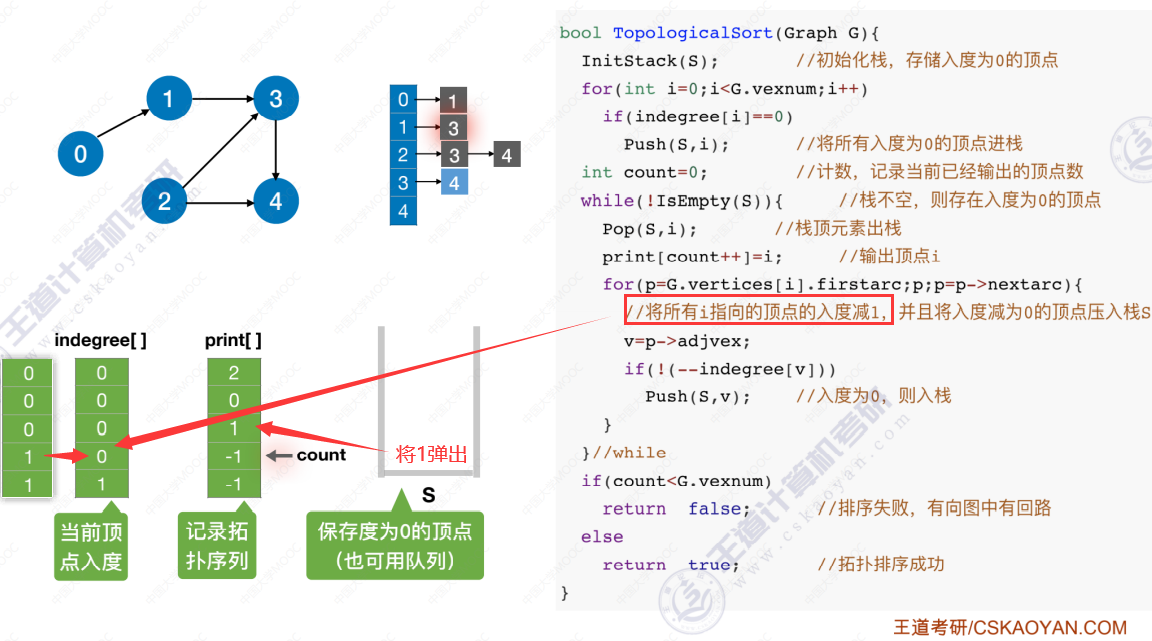
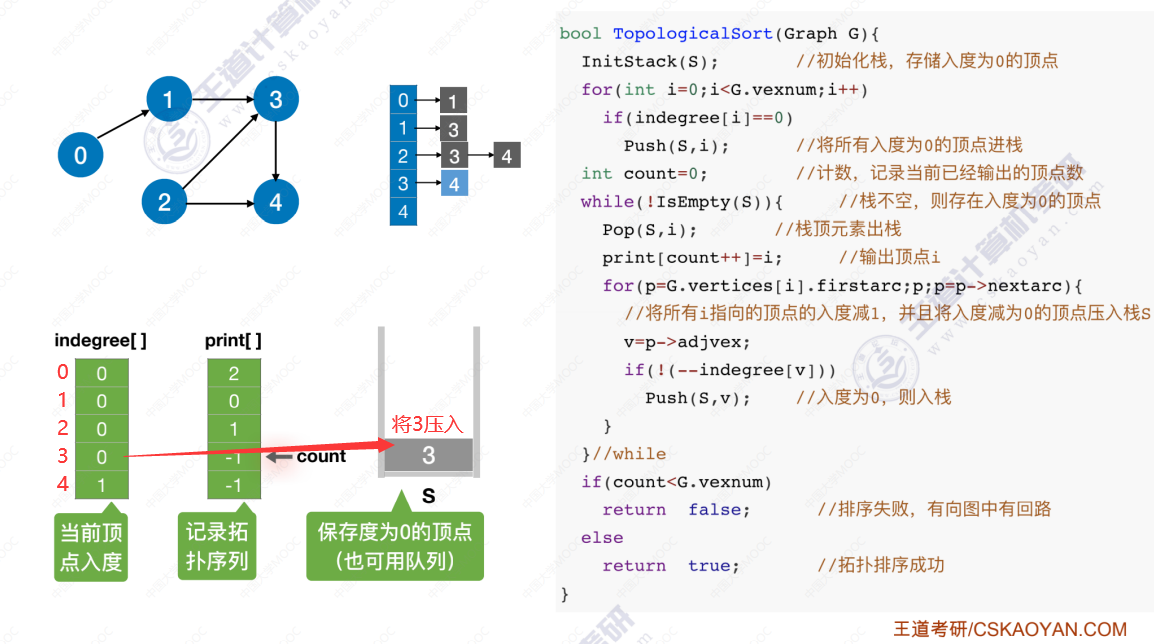
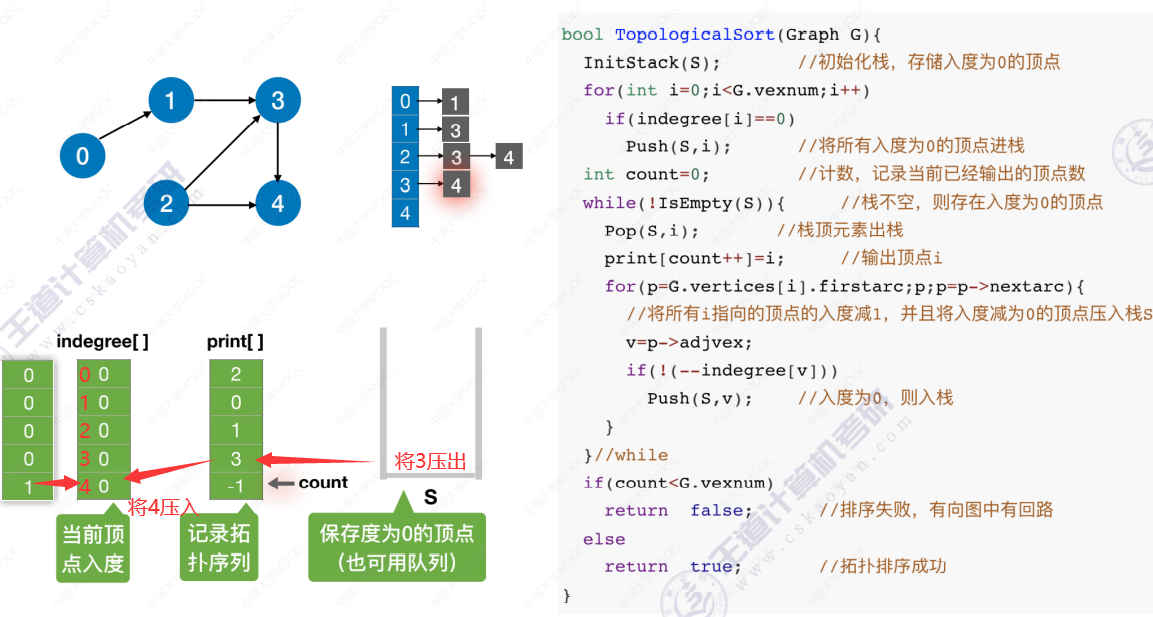
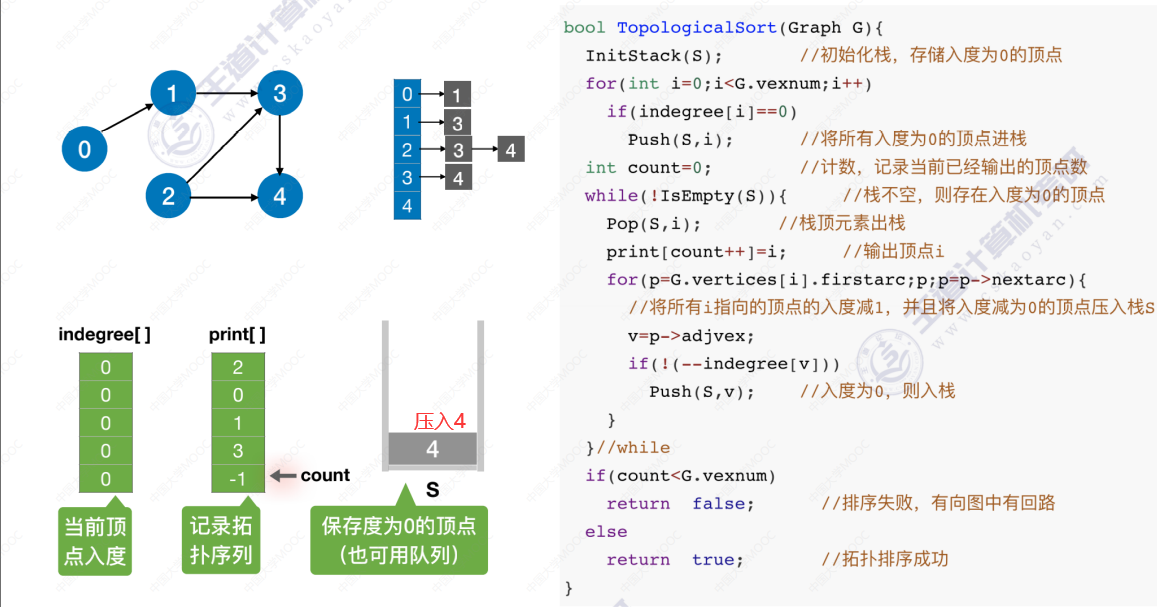
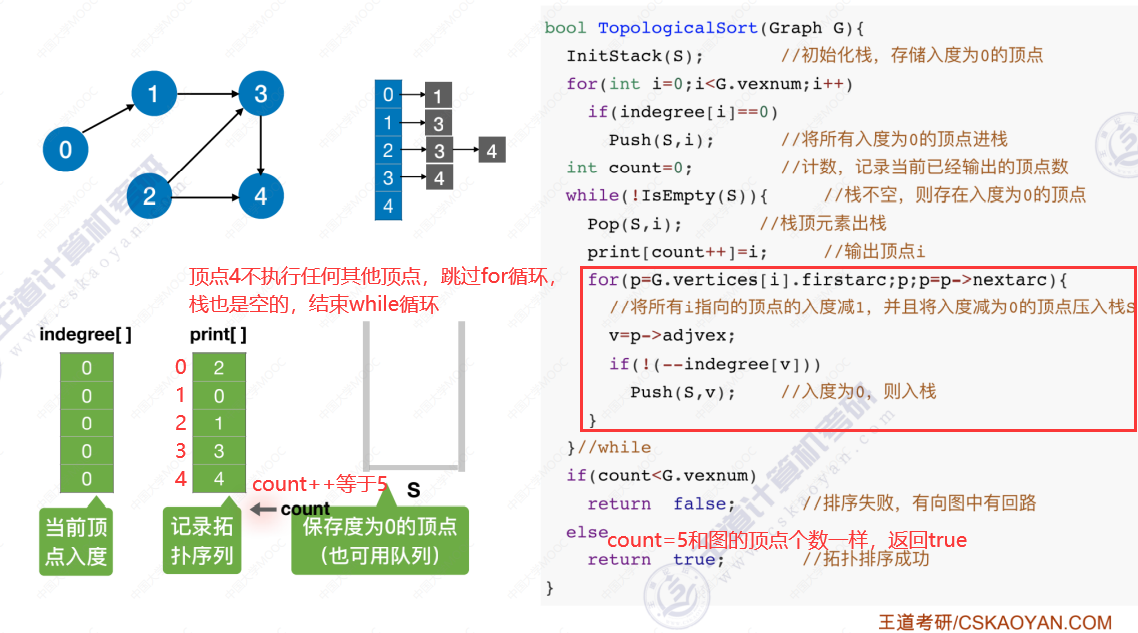
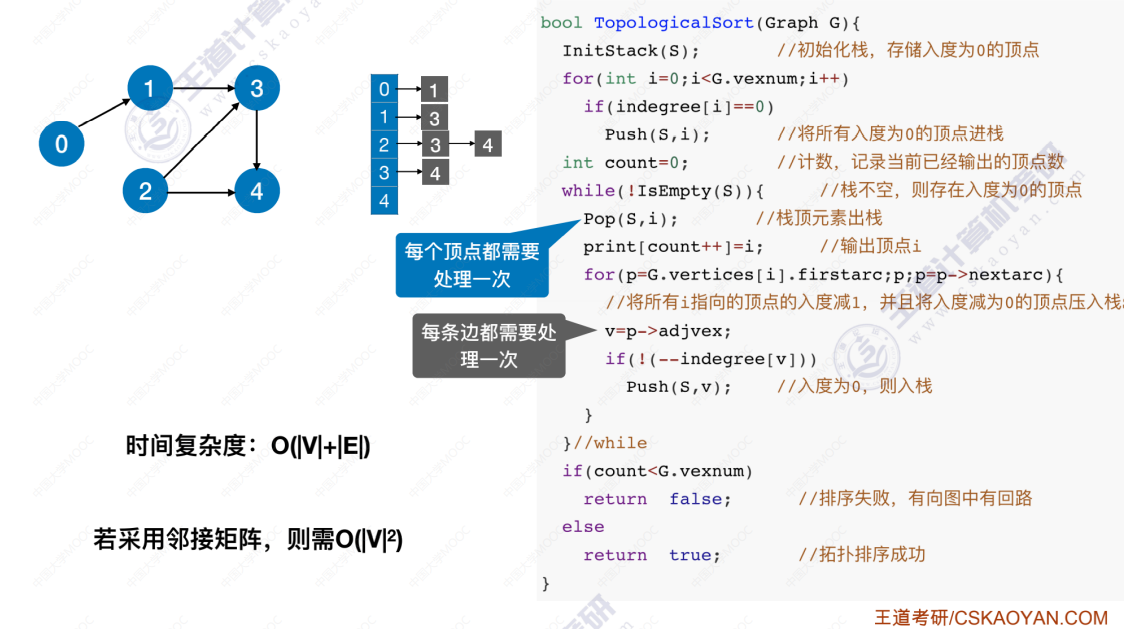
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述

    时间复杂度分析

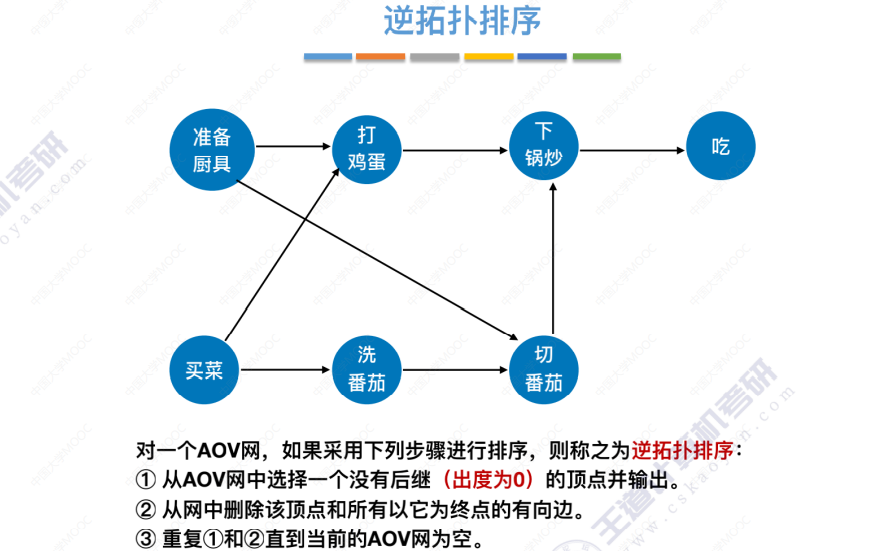
    在这里插入图片描述

    逆拓扑排序

    逆拓扑排序引入

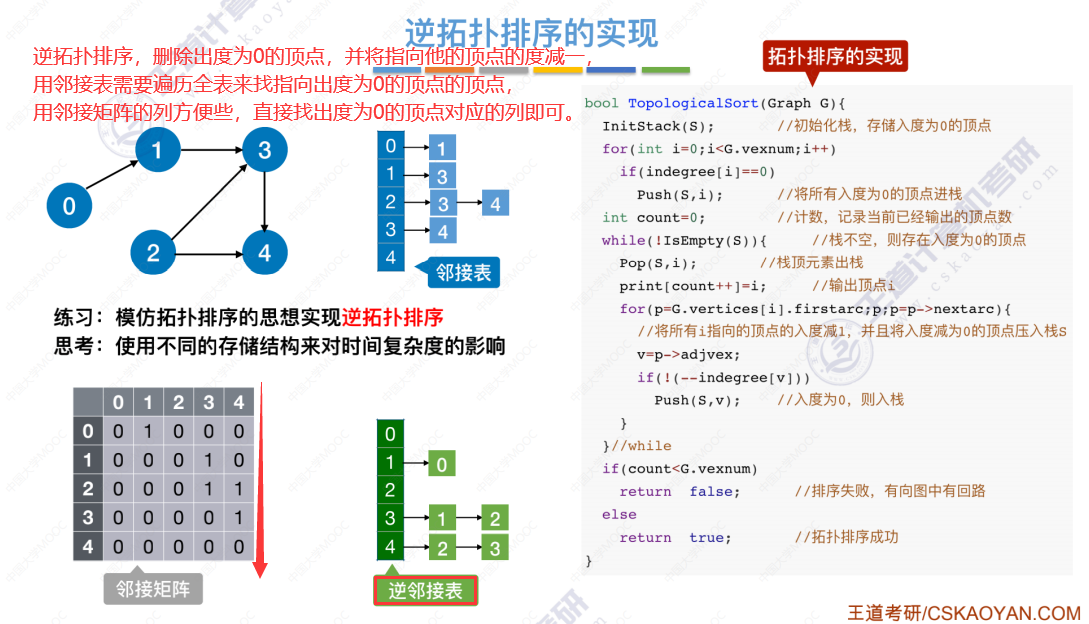
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述

    逆拓扑排序的实现（DFS算法深度优先）

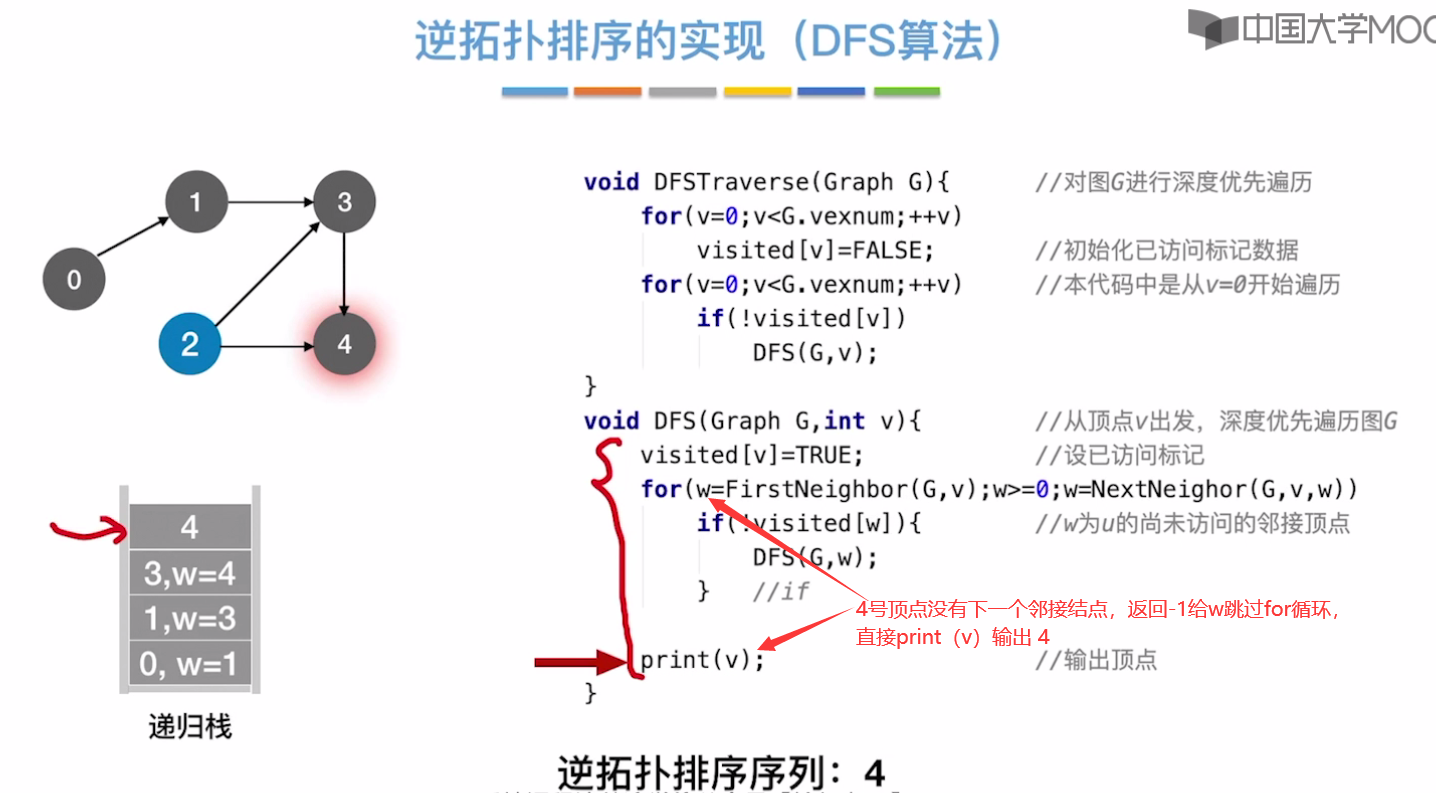
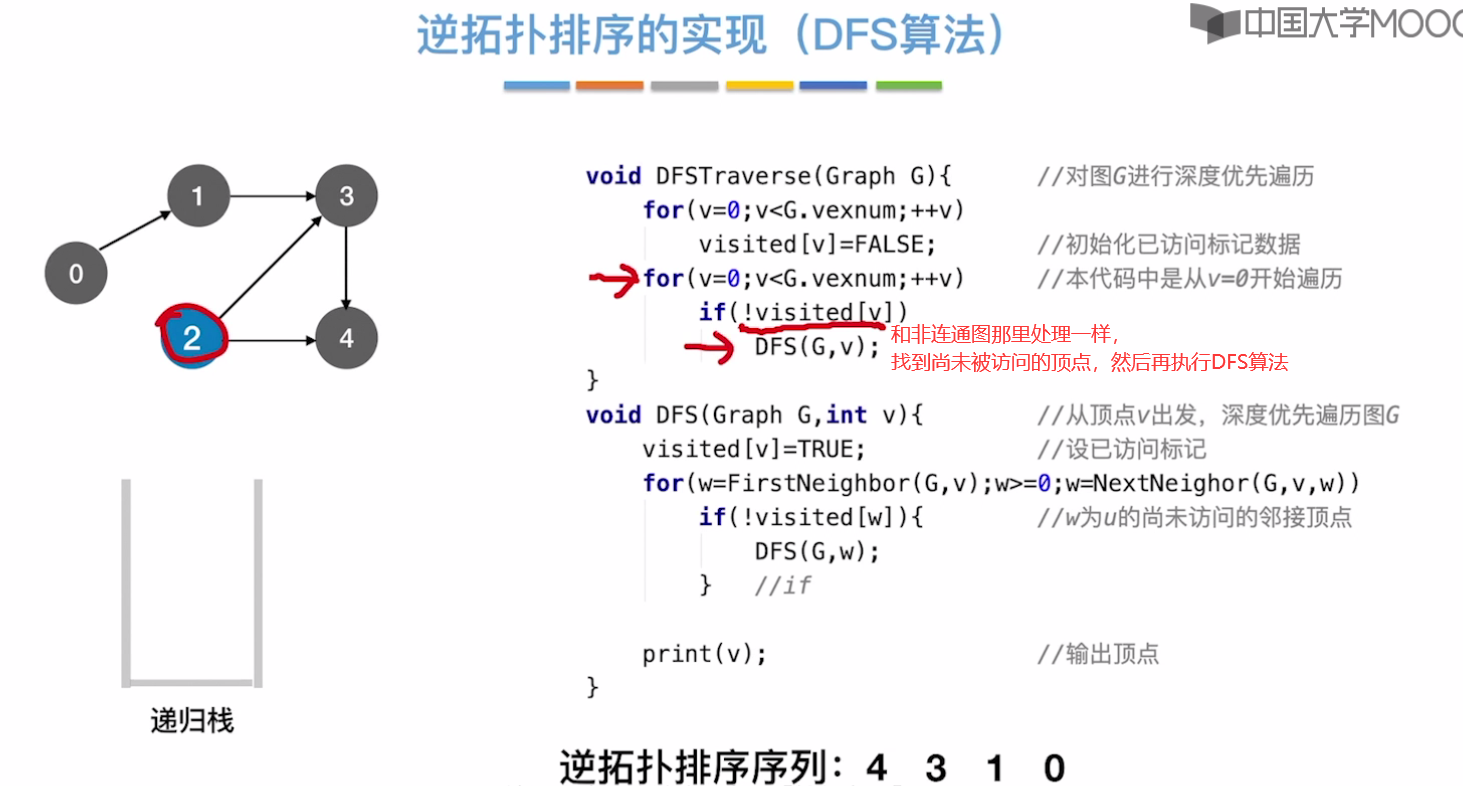
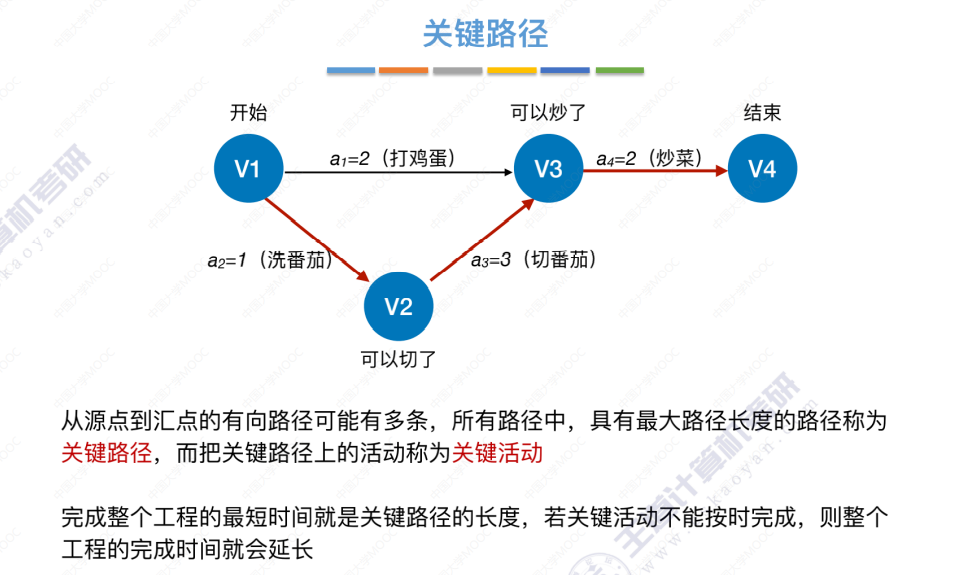
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述

    6.4-7 关键路径

    概念引入

    事件是一瞬间完成的。
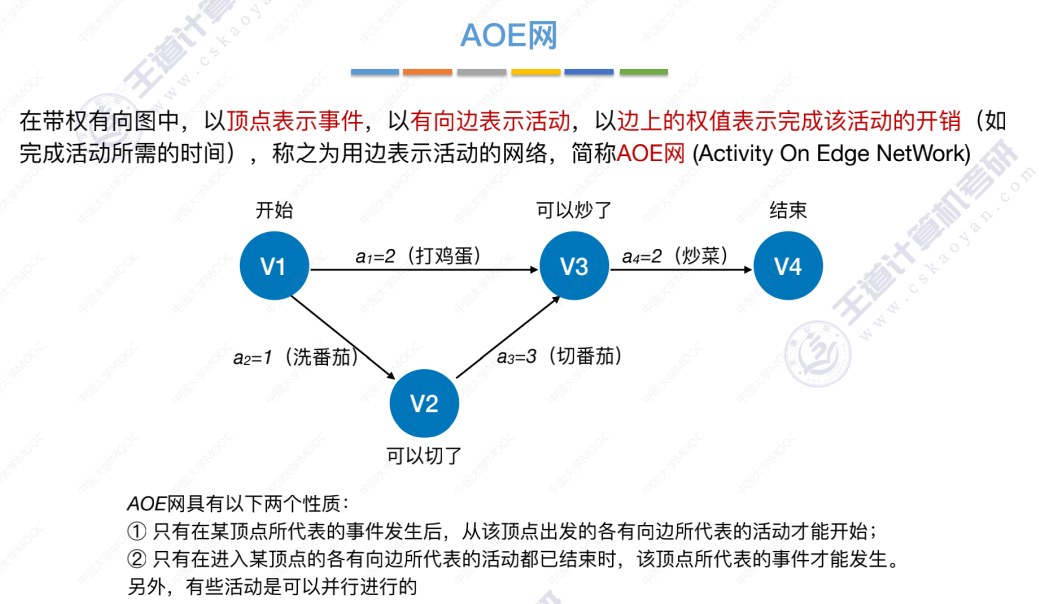
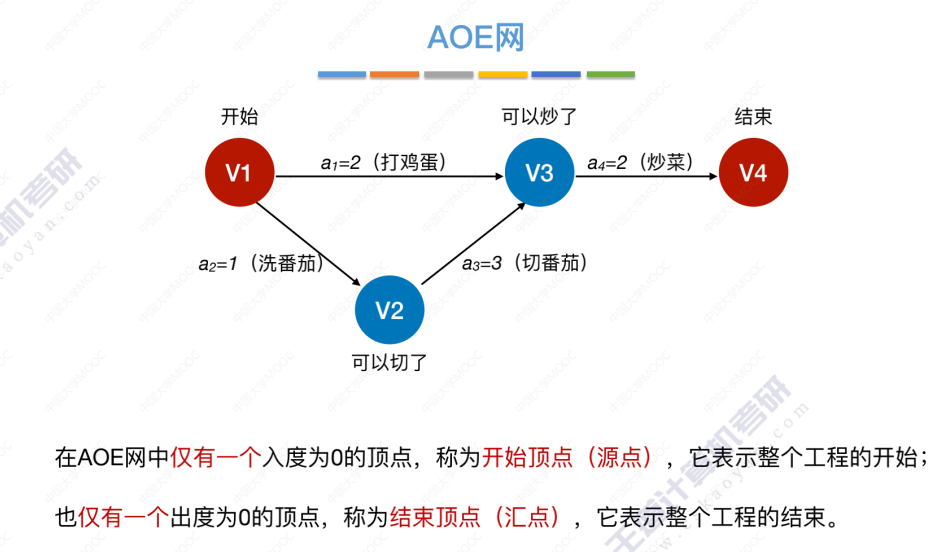
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述

    求关键路径的步骤

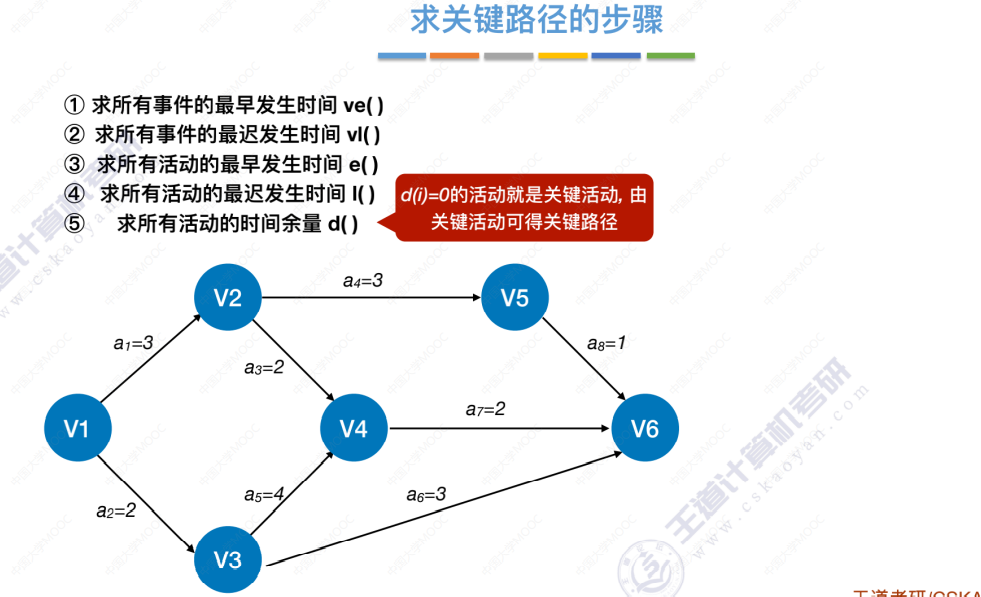
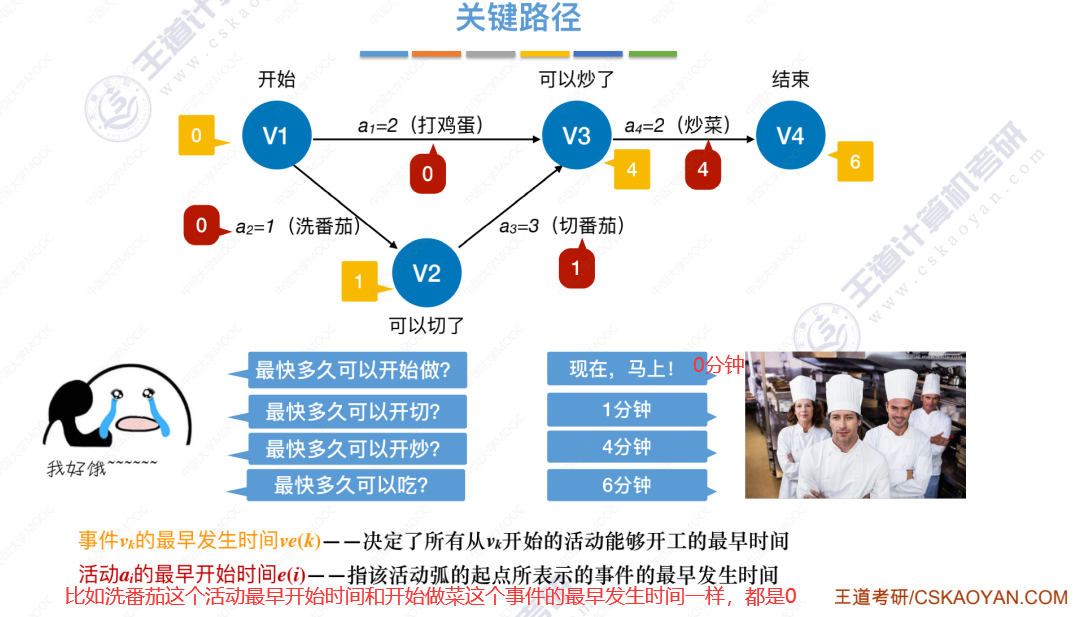
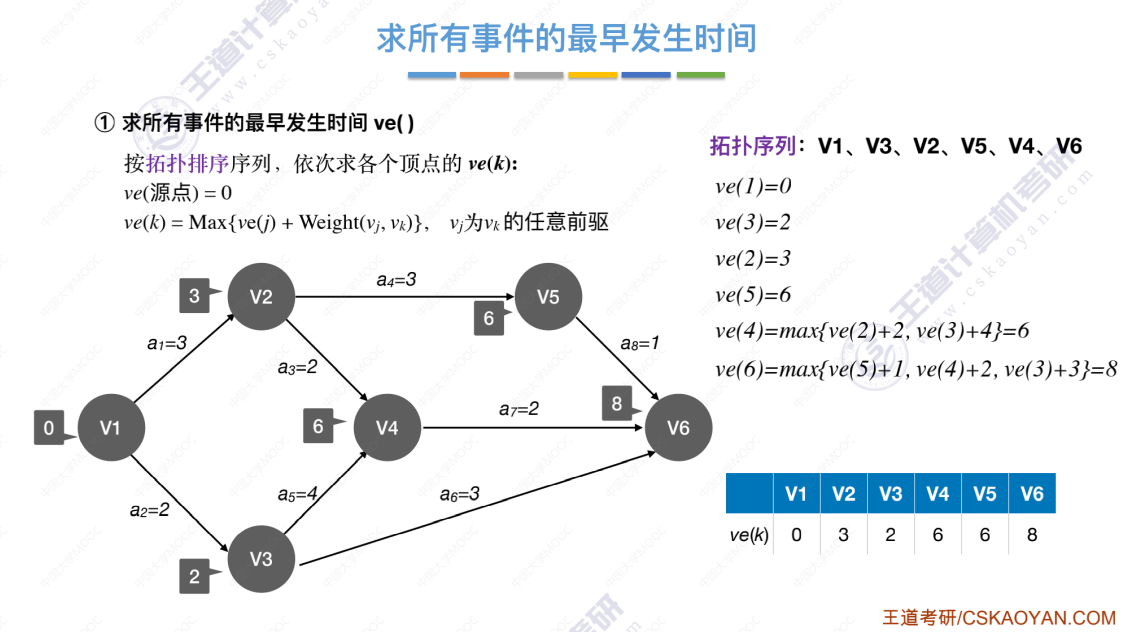
    在这里插入图片描述

    1、求所有 事件 的最早发生时间

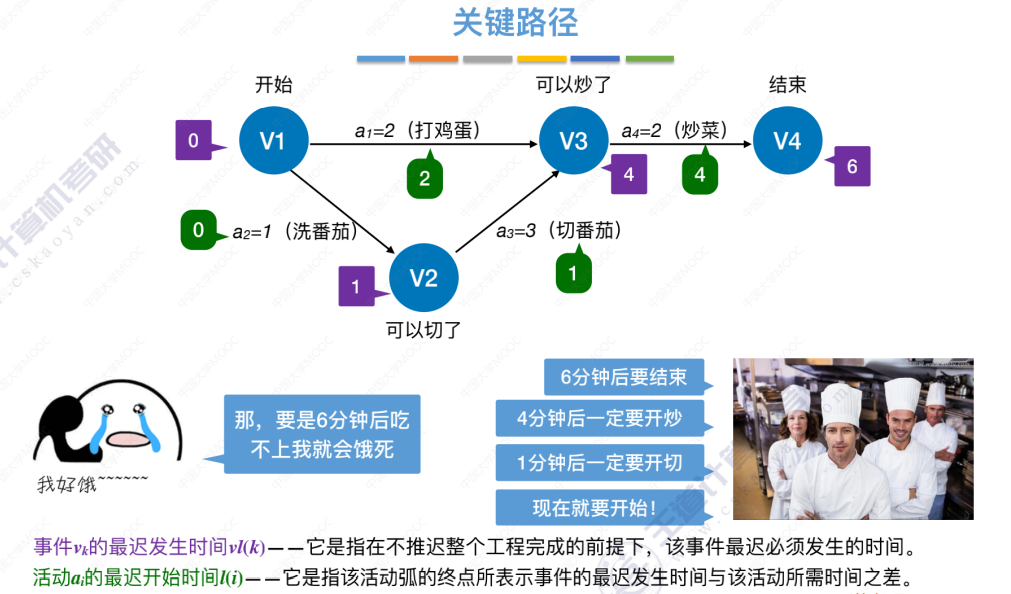
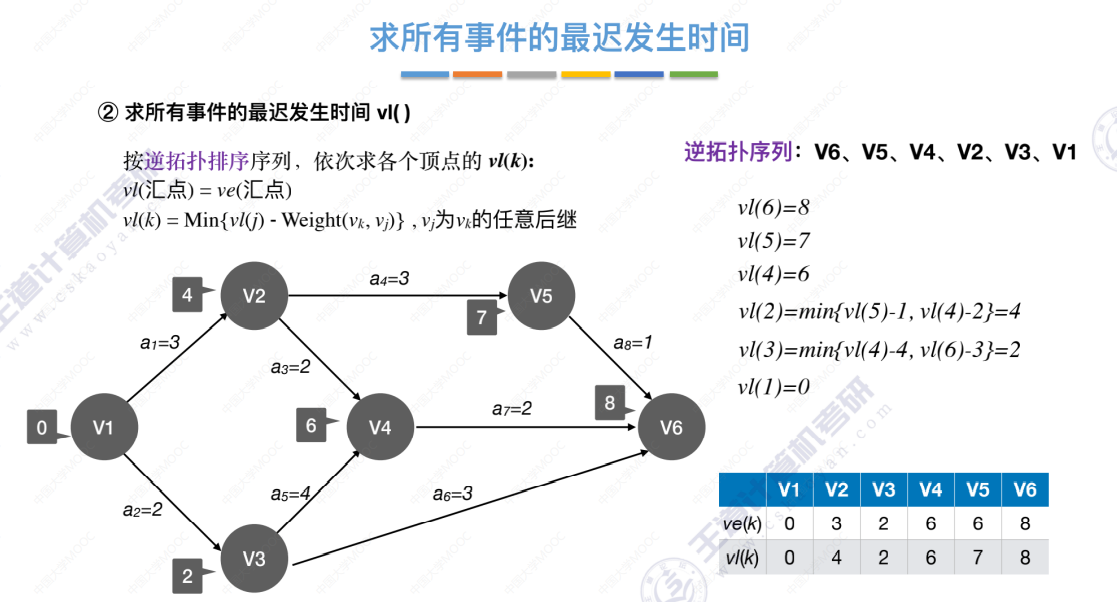
    在这里插入图片描述

    2、求所有 事件 的最迟发生时间

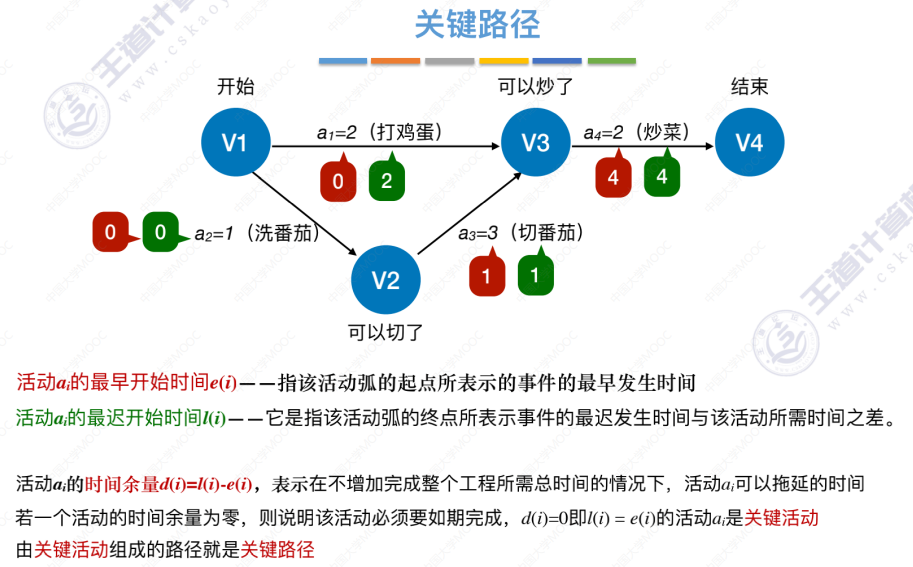
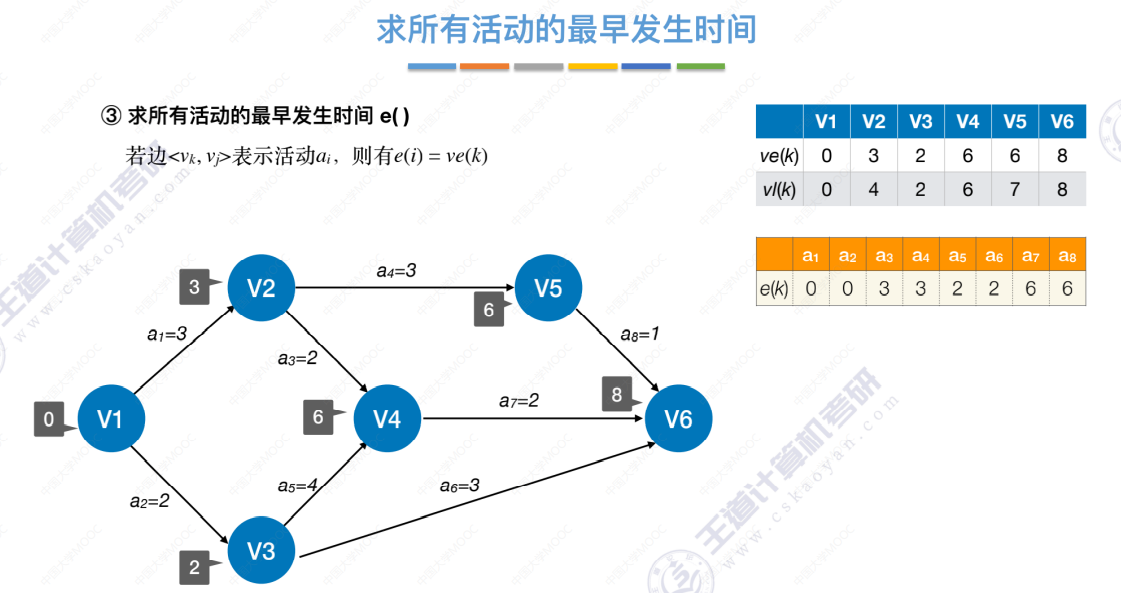
    在这里插入图片描述

    3、求所有 活动 的最早发生时间

    每个活动的最早发生时间，就是这个活动的弧尾所连的这个事件的最早发生时间
    在这里插入图片描述

    4、求所有 活动 的最迟发生时间

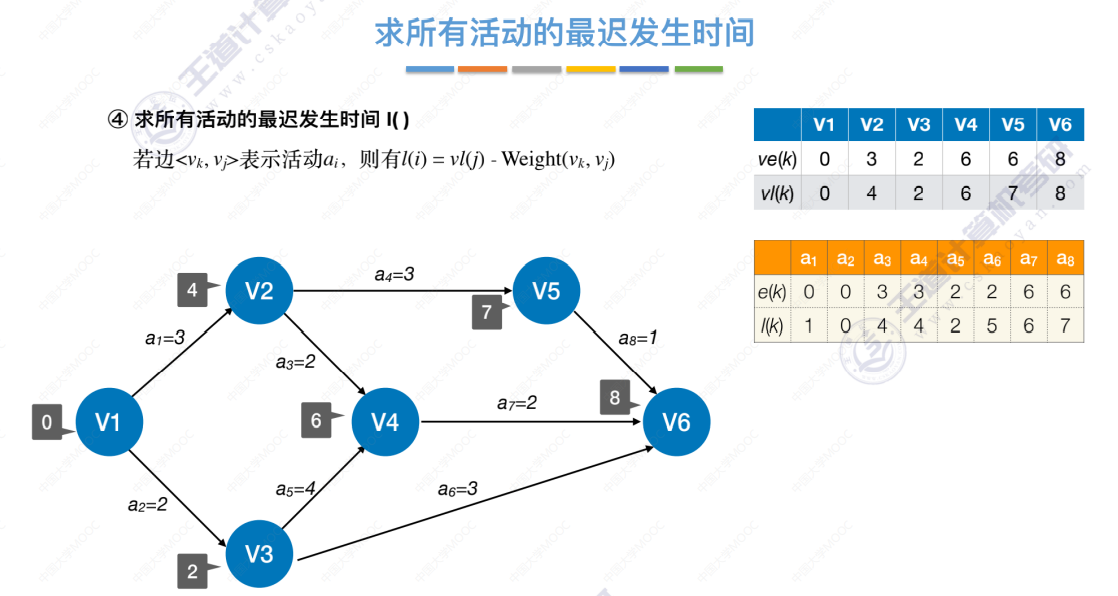
    在这里插入图片描述

    5、求所有 活动 的时间余量d（）

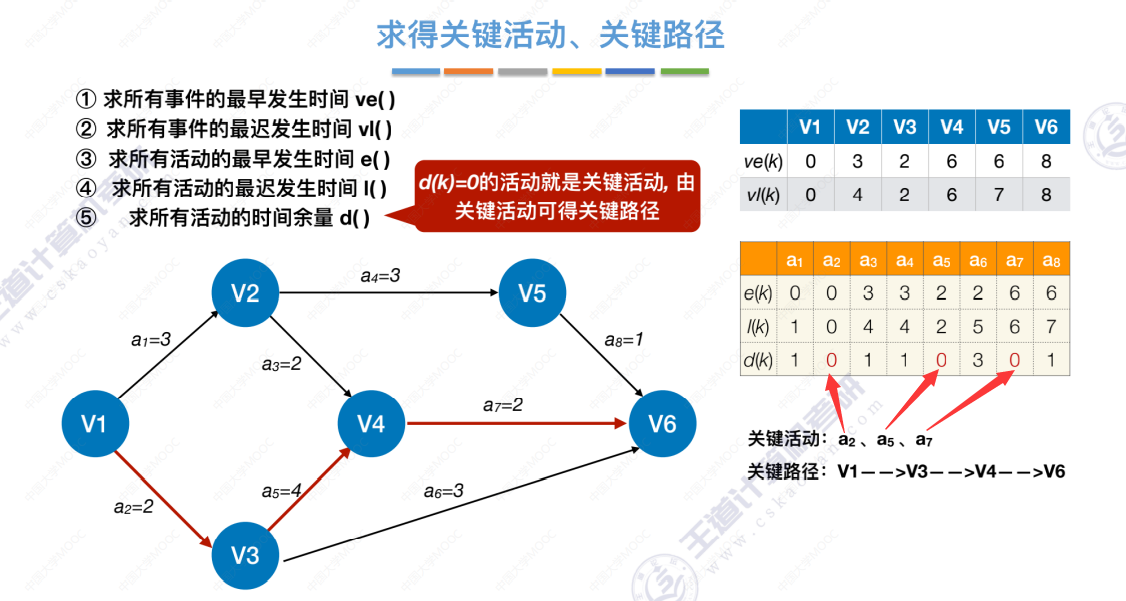
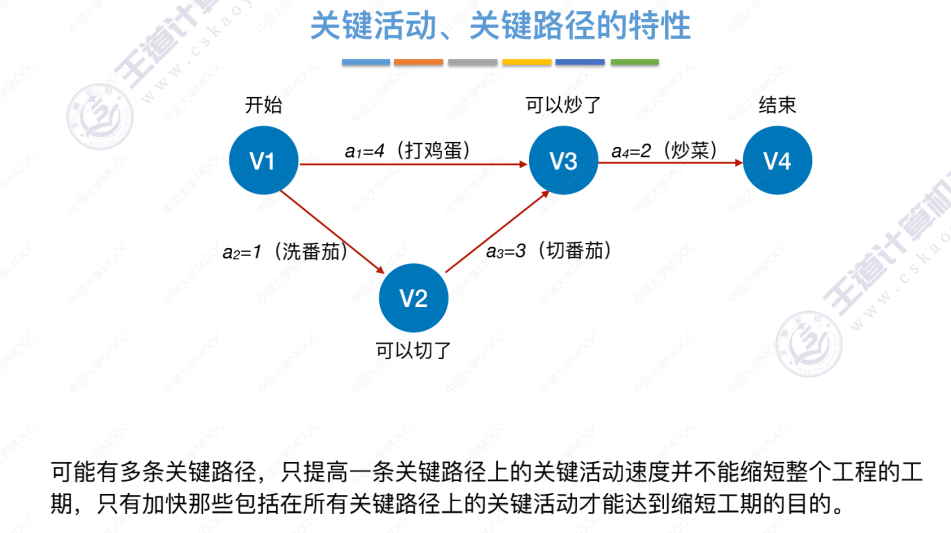
    在这里插入图片描述

    关键活动、关键路径的特性

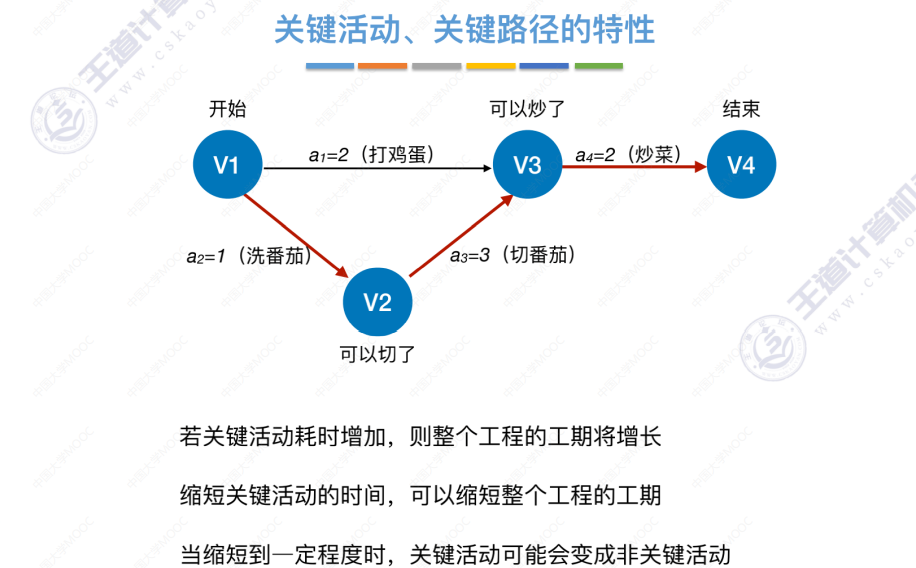
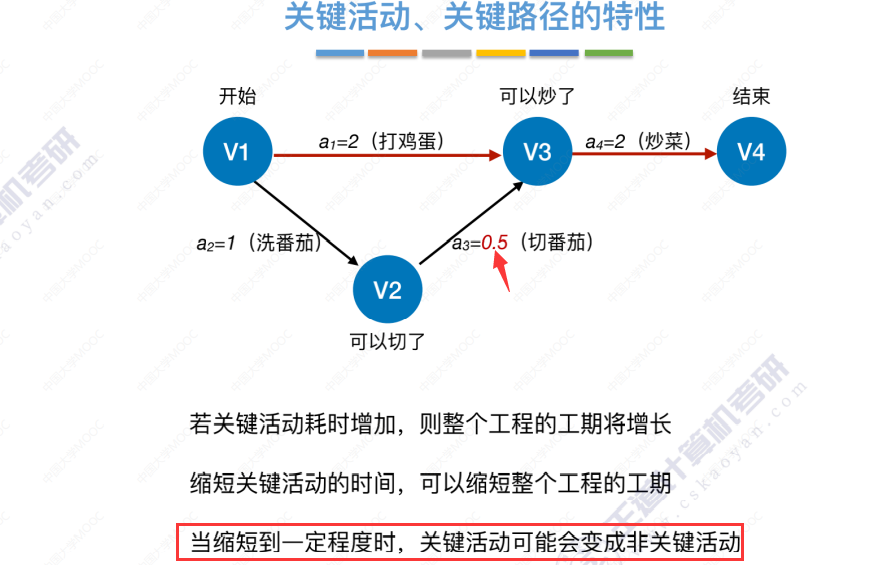
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述

  • 相关阅读:
    MySQL第四讲·如何正确设置主键？
    华为机试 - 最大社交距离
    Kuboard突然无法访问提示：Failed to connect to the database
    WEB自动化-04-Cypress 测试用例编写和组织
    室内渲染的艺术：创造理想空间的视觉魔法！
    cfssl自签证书
    从容器化到资源池化，数栈云原生技术实践探索之路
    域名解析中的A记录和CNAME什么意思
    java继承的优缺点分析
    数据挖掘学习笔记02——算法（分类、聚类、回归、关联）
  • 原文地址：https://blog.csdn.net/qq_32480989/article/details/126193687