目录

一、极大似然估计

二、误差的高斯分布与最小二乘估计的等价性

---

一、极大似然估计

x表示概率，θ表示要估计的参数。

我们定义一个极大似然函数，使这个函数最大。

直接对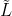求导比较麻烦，所以我们将似然函数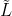转化成对数的形式，来求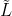的最大值

举个例子：

高斯分布和样本如下所示：

 定义对数似然函数：

要求L的最大值，就需要求导。

对u求偏导：

这个u实际上就是样本均值。

对σ求偏导：

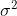 实际上就是方差。

那么，样本方差与极大似然估计的方差有什么区别呢？

答：极大似然估计出来的方差是有偏估计。

二、误差的高斯分布与最小二乘估计的等价性

x为n维的矩阵，y为实数。

我们定义一个多元线性方程

拟合误差为：

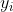为真实值，是拟合出来的值。 

 假设误差服从标准正态分布：

 我们定义一个极大似然函数：

 则最大化似然函数L，相当于最小化，即最小化拟合误差。

如何对J进行最小化呢？

求导得到：

 移项得到：​​​​​​​

 

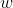我们对进行变换，和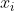为两个列向量，则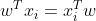是一个实数，最终变换为。

即得到：

 

则w等于：

对比之前讲到的最小二乘得到的结果

可以看到二者是相同的。

附链接：数学基础（二）逆矩阵、伪逆矩阵、最小二乘解、最小范数解