引入

大家都用过搜索引擎吧，在输入关键字时，下面的提示框会不断快速变化，里面的内容是一些以目前输入关键字开头的搜索记录，而且我们每次的搜索也会被加入到数据库中。

这个功能是怎么实现的呢？总不能遍历整个数据库呀，请看下文Trie树。

算法

理论

Trie树的基本功能是在支持插入、删除的情况下动态维护以一个前缀开头的所有字符串，那其存储有何特点？

1. 根节点为空（实现时令其存储特殊字符，如#），其余每个结点存一个字符；
2. 每个结点所有子结点存储字符各不相同；
3. 对于每个字符串，树中都有且仅有一条链使从上到下将此链中所有字符拼接后为此字符串；
4. 所以，一个点可以表示一个字符串（后续称其为此点的字符串），以此点子树结点结尾的字符串均以此点的字符串为前缀；
5. 因每个结点只存一个字符，使用时需注意空间。

---

刚才的叙述可能有些不好理解，让我们来看一个具体的案例，如图为以字符串"az",“app”,“apple”,“iak”,“ice”,“iakioi”,"iaknoi"构造的Trie树：

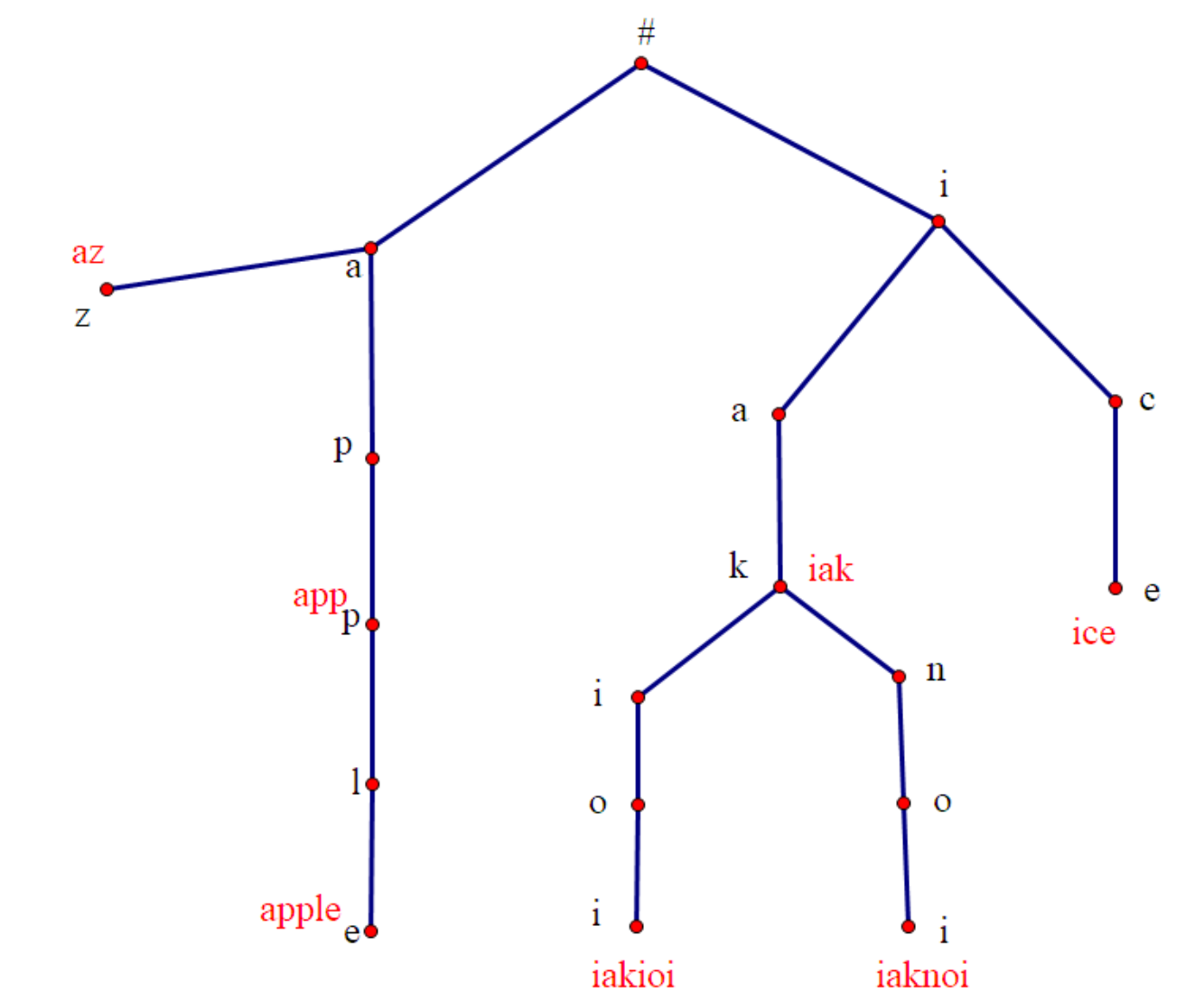
实现

为方便实现，假设所有字符串均由小写字母构成。

---

初始化
令$N$为需要的结点个数（即所有字符串长度之和），令$L$为每个结点最大子结点数（即字符串每位有多少种可能）。

• 定义$t_u{,}_c$为编号$u$的结点的值为$c$的子结点编号，不存在则为$-1$；
• 定义$cn{t}_u$为以编号为$u$结点结尾的字符串数量（即所有字符串中$u$的字符串的数量）；
• 定义$k$为不含根节点的结点总数。

const int N = 1e5 + 5, L = 26;
struct Trie {
	int t[N][L], cnt[N], k;
	void init() {
		memset(t, -1, sizeof t);
		memset(cnt, 0, sizeof cnt);
		k = 0;
	}
};
1
2
3
4
5
6
7
8
9

插入
在树中找到其前缀的链，若不能完全包含这个字符串则新建剩下的结点。

void insert(char *s) {
	int u = 0;	// u: 当前结点
	for (int i = 0; s[i]; ++i) {	// 寻找前缀链
		int &v = t[u][s[i] ^ 'a'];	// 下一位结点
		if (v == -1) {	// 若没有：新建
			v = ++k;
        }
		u = v;	// 迭代
	}
	++cnt[u];	// 记录结束位置
}
1
2
3
4
5
6
7
8
9
10
11

删除
同理，沿链寻找其结束结点，将此位置结束的字符串数$-1$即可。

void erase(char *s) {
	int u = 0;
    for (int i = 0; s[i]; ++i) {
        int v = t[u][s[i] ^ 'a'];
        if (v == -1) {
            return ;
        }
        u = v;
    }
    if (cnt[u]) {
        --cnt[u];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13

查询
同理，返回：此字符串出现次数。

int find(char *s) {
	int u = 0;
    for (int i = 0; s[i]; ++i) {
        int v = t[u][s[i] ^ 'a'];
        if (v == -1) {
            return 0;
        }
        u = v;
    }
    return cnt[u];
}
1
2
3
4
5
6
7
8
9
10
11

最终代码

const int N = 1e5 + 5, L = 26;
struct Trie {
	int t[N][L], cnt[N], k;
	void init() {
		memset(t, -1, sizeof t);
		memset(cnt, 0, sizeof cnt);
		k = 0;
	}
    void insert(char *s) {
        int u = 0;
        for (int i = 0; s[i]; ++i) {
            int &v = t[u][s[i] ^ 'a'];
            if (v == -1) {
                v = ++k;
            }
            u = v;
        }
        ++cnt[u];
    }
    int find(char *s) {
        int u = 0;
        for (int i = 0; s[i]; ++i) {
            int v = t[u][s[i] ^ 'a'];
            if (v == -1) {
                return 0;
            }
            u = v;
        }
        return cnt[u];
    }
    void erase(char *s) {
        int u = 0;
        for (int i = 0; s[i]; ++i) {
            int v = t[u][s[i] ^ 'a'];
            if (v == -1) {
                return ;
            }
            u = v;
        }
        if (cnt[u]) {
            --cnt[u];
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

习题

最大异或对

题意：给定一个数组$a_{\mathrm{1...}n}$，求 m a x { a i x o r a j } max\{a_i xor a_j\} max{ai​xoraj​}。
题解：考虑在线处理，求出目前值和之前值的最大异或再取最大，如何求出？因为异或为二进制运算，则从前往后每次考虑当前位最优，即如果有的话就取目前二进制位的取反，这里就需要Trie的维护，只不过存储的不是字符串而是二进制位。

字符串拼接

题意：给定一个字符集$S$和一个字符串$T$，求用$S$中字符串拼接成$T$的方案数。
题解：很容易想到dp，定义$f_i$为$T$前$i$位的答案；递推式也显而易见，若$T_{j...i}$在$S$中出现过，$f_i+=f_j-1$，这里是否出现就需要用Trie维护。

最长公共前缀期望

题意：给定字符集，求其中任意两个字符串最长公共前缀的期望值。
题解：我们知道$E=\sum P\times X$，所以我们可以在以此字符集建立的Trie中枚举当前点$u$是最长公共前缀结尾的情况数再除以总情况数即可。对于以$u$为结尾的情况，我们分三种情况讨论：第一种，两个串的结尾在$u$两个子树中；第二种，一个以$u$结尾，另一个以其子树中点结尾；第三种，均以$u$结尾。

今天的复习内容就到这里，感谢收看~