1.算术三元组的数目

6136. 算术三元组的数目

题目描述

代码分析

我的解题思路就是模拟，两个for循环（因为数据范围小，比较快就做出来了）
看题解，还有哈希表和三指针。
哈希表：先用哈希表保存所有值，遍历所有值的时候，看是否有nums[i] -diff和nums[i]+diff即可，真的确实简单。
三指针：利用三个指针遍历三个点，因为是严格递增，所以当找到遍历下个结点时，其余两个指针也是在原本基础上加，这样对于空间是O(1)，注意需要判断指针是否在范围内。

AC代码

class Solution {
public:
    int vis[205];
    int arithmeticTriplets(vector<int>& nums, int diff) {
        memset(vis,0,sizeof(vis));
        int res=0;
        int size=nums.size();
        for(int i=0;i<size;i++)
        {
            int pre=nums[i];
            int mid=1;
            for(int j=i+1;j<size;j++)
            {
                if(vis[j])continue;
                if(nums[j]-pre>diff)break;
                else if(nums[j]-pre==diff)
                {
                    pre=nums[j];
                    mid++;
                    vis[j]=1;
                }
            }
            if(mid>=3)res+=mid-2;
        }
        return res;
    }
};

// 哈希表
class Solution {
public:
    int arithmeticTriplets(vector<int>& nums, int diff) {
        unordered_map<int,int> m;
        int res=0;
        for(auto it:nums)m[it]++;
        for(auto it:nums)
            if(m[it-diff]&&m[it+diff])res++;
        return res;
    }
};

// 三指针
class Solution {
public:
    int arithmeticTriplets(vector<int>& nums, int diff) {
        int i=0,j=1,k=2,res=0;
        int size=nums.size();
        for(i=0;i<size;i++)
        {
            while(j<size&&nums[j]-nums[i]<diff)j++;
            if(j==size||nums[j]-nums[i]!=diff)continue;
            while(k<size&&nums[k]-nums[j]<diff)k++;
            if(k<size&&nums[j]-nums[i]==diff&&nums[k]-nums[j]==diff)res++;
        }
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57

2.受限条件下可到达节点的数目

6139. 受限条件下可到达节点的数目

题目描述

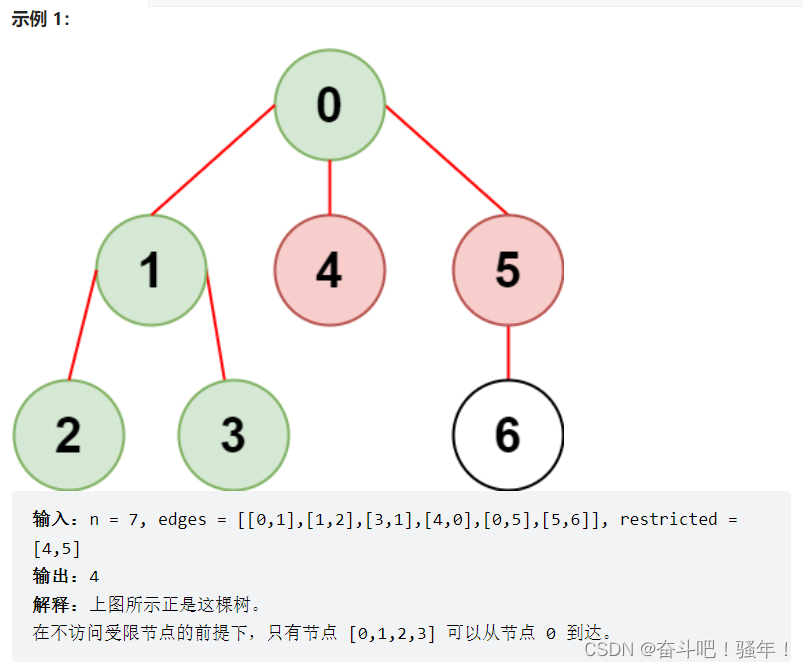
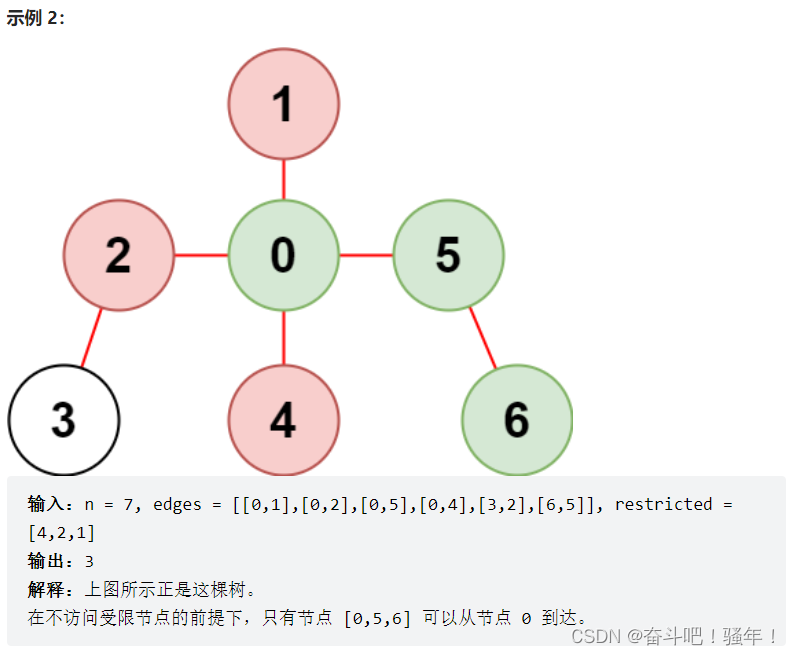
代码分析

这道题其实就是考图的遍历，用BFS和DFS都可以，我用的BFS。
我们用数组保存结点是否访问，那么受限的点我们标记已经访问即可

AC代码

class Solution {
public:
    unordered_map<int,vector<int>> m;
    int vis[100010];
    int reachableNodes(int n, vector<vector<int>>& edges, vector<int>& restricted) {
        memset(vis,0,sizeof(vis));
        // 邻接表存图
        for(auto it:edges)
        {
            int a=it[0],b=it[1];
            m[a].push_back(b);
            m[b].push_back(a);
        }
        // 将不能到达的点置为已访问
        for(auto it:restricted)vis[it]=1;
        
        queue<int> q;
        q.push(0);
        vis[0]=1;
        while(!q.empty())
        {
            int s=q.front();
            for(auto it:m[s])
            {
                if(!vis[it])q.push(it);
                vis[it]=1;
            }
            q.pop();
        }
        int res=0;
        for(int i=0;i<n;i++)if(vis[i])res++;
        return res-restricted.size();
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

3.检查数组是否存在有效划分

6137. 检查数组是否存在有效划分

题目描述

代码分析

这道题使用动态规划，dp[i] 表示从起点到当前点是否可以有效划分
这道题只要想到走阶梯就可以了，我们可以走两步或者走三步，问是否能到达终点
那么根据题目给出的三个条件就可以写出三个状态转移方程（解题下标是从下标0开始，这里为了方便从1开始）
1.dp[i-2]&&nums[i]==nums[i-1]
2.dp[i-3]&&nums[i]-nums[i-1]==1&&nums[i-1]-nums[i-2]==1
3.dp[i-3]&&nums[i]==nums[i-1]&&nums[i-1]==nums[i-2]
意思就是如果在红色箭头处可以划分为true，那么当前黑色箭头处也就为true

AC代码

class Solution {
public:
    int dp[100010];
    bool validPartition(vector<int>& nums) {
        memset(dp,0,sizeof(dp));
        dp[0]=1;
        for(int i=1;i<nums.size();i++)
        {
            if(dp[i-1]&&nums[i]==nums[i-1])dp[i+1]=1;
            if(i>1)
            {
                if(dp[i-2]&&nums[i]-nums[i-1]==1&&nums[i-1]-nums[i-2]==1)dp[i+1]=1;
                if(dp[i-2]&&nums[i]==nums[i-1]&&nums[i-1]==nums[i-2])dp[i+1]=1;
            }
        }
        if(dp[nums.size()])return true;
        else return false;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

4.最长理想子序列

6138. 最长理想子序列

题目描述

代码分析

使用哈希表对DP进行空间优化
哈希表保存以某个字母为结尾的最大值，当前最大值就遍历哈希表中范围的字母即可

AC代码

class Solution {
public:
    unordered_map<int,int> m;
    int longestIdealString(string s, int k) {
        int res=1;
        m[s[0]]=1;
        for(int i=1;i<s.size();i++)
        {
            // 求出当前字母绝对值差的范围
            int minc=s[i]-k,maxc=s[i]+k;
            if(minc<'a')minc='a';
            if(maxc>'z')maxc='z';
            // 用中间
            int mid=1;
            for(int j=minc;j<=maxc;j++)
            {
                mid = max(mid,m[j]+1);
            }
            m[s[i]]=mid;
            res=max(res,m[s[i]]);
        }
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

总结感想

这次其实总体来说都不难，但是我在第三题想了很久没想出来（其实如果想到走阶梯那么很快就想出来了），动态规划的题不能细想，太往里面想容易出不来。其他的题虽然做出来了，但是还是要学习大佬们更简单的做法。
多总结反思，多刷题！！！