知识点

---

---

模板题：洛谷 B3609 [图论与代数结构 701] 强连通分量

题目描述

给定一张 n 个点 m 条边的有向图，求出其所有的强连通分量。

注意，本题可能存在重边和自环。

输入格式

第一行两个正整数 n ， m ，表示图的点数和边数。

接下来 m 行，每行两个正整数 u 和 v 表示一条边。

输出格式

第一行一个整数表示这张图的强连通分量数目。

接下来每行输出一个强连通分量。第一行输出 1 号点所在强连通分量，第二行输出 2 号点所在强连通分量，若已被输出，则改为输出 3 号点所在强连通分量，以此类推。每个强连通分量按节点编号大小输出。

输入输出样例

输入 #1

6 8
1 2
1 5
2 6
5 6
6 1
5 3
6 4
3 4

输出 #1

3
1 2 5 6
3
4

说明/提示

对于所有数据，，。

---

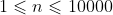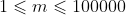#include 
#include 
#include 
#include 
#include 
using namespace std;
int n,m;
const int maxn=1e6+5;
struct node
{
	int to,next;
}edge[maxn<<1];
int head[maxn],num=0,cnt=0,ans=0,top=0;
int dfn[maxn],low[maxn],stac[maxn],color[maxn],size[maxn];
bool vis[maxn];
inline int read()
{
	int x=0,f=1;
	char c=getchar();
	while(c<'0'||c>'9')
	{
		if(c=='-') f=-1;
		c=getchar();
	}
	while(c>='0' && c<='9')
	{
		x=(x<<3)+(x<<1)+(c^48);
		c=getchar();
	}
	return x*f;
}
 
inline void add(int u,int v)
{
	edge[++num].to=v;
	edge[num].next=head[u];
	head[u]=num;
}
 
inline void tarjan(int u)
{
	dfn[u]=low[u]=++cnt;
	vis[u]=1;
	stac[++top]=u;
	for(int i=head[u];i!=-1;i=edge[i].next)
	{
		int v=edge[i].to;
		if(!dfn[v])
		{
		tarjan(v);
		low[u]=min(low[u],low[v]);	
		} 
		else if(vis[v])
			{
				low[u]=min(low[u],dfn[v]);
			}	
	}
	
	if(dfn[u] == low[u])
	{
		ans++;
		color[u]=ans;
		while(stac[top]!=u)
		{
			vis[stac[top]]=0;
			color[stac[top]]=ans;
			--top;
		}
		vis[u]=0;
		--top;
	}
}
 
int main()
{
	n=read(); m=read();
	memset(head,-1,sizeof(head));
	for(int i=1;i<=m;++i)
	{
		int u=read(),v=read();
		add(u,v);
	}
	
	for(int i=1;i<=n;++i)
	{
		if(!dfn[i]) tarjan(i);
	}
	
	bool pr[maxn];
	printf("%d\n",ans);
 
	for(int i=1;i<=n;++i) //这道题的难点就在于最后的输出
	{
		if(pr[i] == 1) continue; //用pr[]标记是否已经输出过
			printf("%d ",i); //没有输出过就输出
			pr[i]=1; //标记，防止重复查找
							
		for(int j=i+1;j<=n;++j)
		{
			if(color[j] == color[i]) //节点j与节点i在同一个强连通分量中
			{
				printf("%d ",j);
				pr[j]=1;
			}
		}
		printf("\n");
	}
	return 0;
}

---

相关练习

1 . 洛谷 P2863 [USACO06JAN]The Cow Prom S 

题目描述

有一个 n 个点，m 条边的有向图，请求出这个图点数大于 1 的强联通分量个数。

输入格式

第一行为两个整数 n 和 m。

第二行至 m+1 行，每一行有两个整数 a 和 b，表示有一条从 a 到 b 的有向边。

输出格式

仅一行，表示点数大于 1 的强联通分量个数。

输入输出样例

输入 #1

5 4
2 4
3 5
1 2
4 1

输出 #1

1

说明/提示

数据规模与约定

对于全部的测试点，保证，，。

---

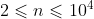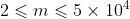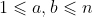#include 
#include 
#include 
#include 
#include 
using namespace std;
int n,m;
const int maxn=1e6+5;
struct node{
	int to,next;
}edge[maxn<<1];
int head[maxn],num=0,cnt=0,top=0,ans=0,sum=0;
int dfn[maxn],low[maxn],stac[maxn],color[maxn],size[maxn];
/* 
    dfn[]用于统计节点是第几个进入dfs递归的；
    low[]用于统计从节点i能到达的已标记过的最远节点；
    stac[]手打栈；
    color[]用于将同一个强连通分量的节点标记为一样的数字，俗称染色；
    size[]用于统计在一个强连通分量中的节点数量，因为只有一个节点也可以被看作一个强连通分量，因此要初始化为1；
*/
 
bool vis[maxn];
inline int read()
{
	int x=0,f=1;
	char c=getchar();
	while(c<'0'||c>'9')
	{
		if(c=='-') f=-1;
		c=getchar();
	}
	while(c>='0' && c<='9')
	{
		x=(x<<3)+(x<<1)+(c^48);
		c=getchar();
	}
	return x*f;
}
 
inline void add(int u,int v)
{
	edge[++num].to=v;
	edge[num].next=head[u];
	head[u]=num;
}
 
inline void tarjan(int u)
{
	dfn[u]=low[u]=++cnt; //输入进来的时候，dfn[]和low[]都标记为第cnt个进入的节点
	vis[u]=1;
	stac[++top]=u; //将节点u存入栈中
	for(int i=head[u];i!=-1;i=edge[i].next)
	{
		int v=edge[i].to; 
		if(!dfn[v]) //如果与节点i相连的节点v没有被找过
		{
		tarjan(v);
		low[u]=min(low[u],low[v]);	//low[]标记为能找到的最早的节点；
		}
		else 
		{
			if(vis[v])
			{
				low[u]=min(low[u],dfn[v]); //dfn[v]也可以改为low[v];
			}
		}	
	}
 
	if(dfn[u] == low[u]) //u为强联通分量的根,也就是能到达的最小节点
	{
		ans++; //统计第几个强连通分量的集
		vis[u]=0;
		while(stac[top]!=u) 
		{
			color[stac[top]]=ans; //染色
			vis[stac[top]]=0; //弹出栈vis恢复
			top--; 
			size[u]++; //强连通分量集内的节点个数加1；
		}
		color[stac[top]]=ans;
		top--;
		if(size[u]>1) sum++;	
	}
	
}
 
int main()
{
	n=read(); m=read();
	memset(head,-1,sizeof(head));
	for(int i=1;i<=m;++i)
	{
		int u=read(),v=read();
		add(u,v);
	}
 
	for(int i=1;i<=n;++i) //在此题中没有这一段初始化就会84pts
	{
		size[i]=1;
	}
 
	for(int i=1;i<=n;++i)
	{
		if(!dfn[i]) //如果该点没有被统计过
		tarjan(i); //继续查找
	}
	printf("%d",sum);
	return 0;
}