一图了解原码、反码、补码的演进历史

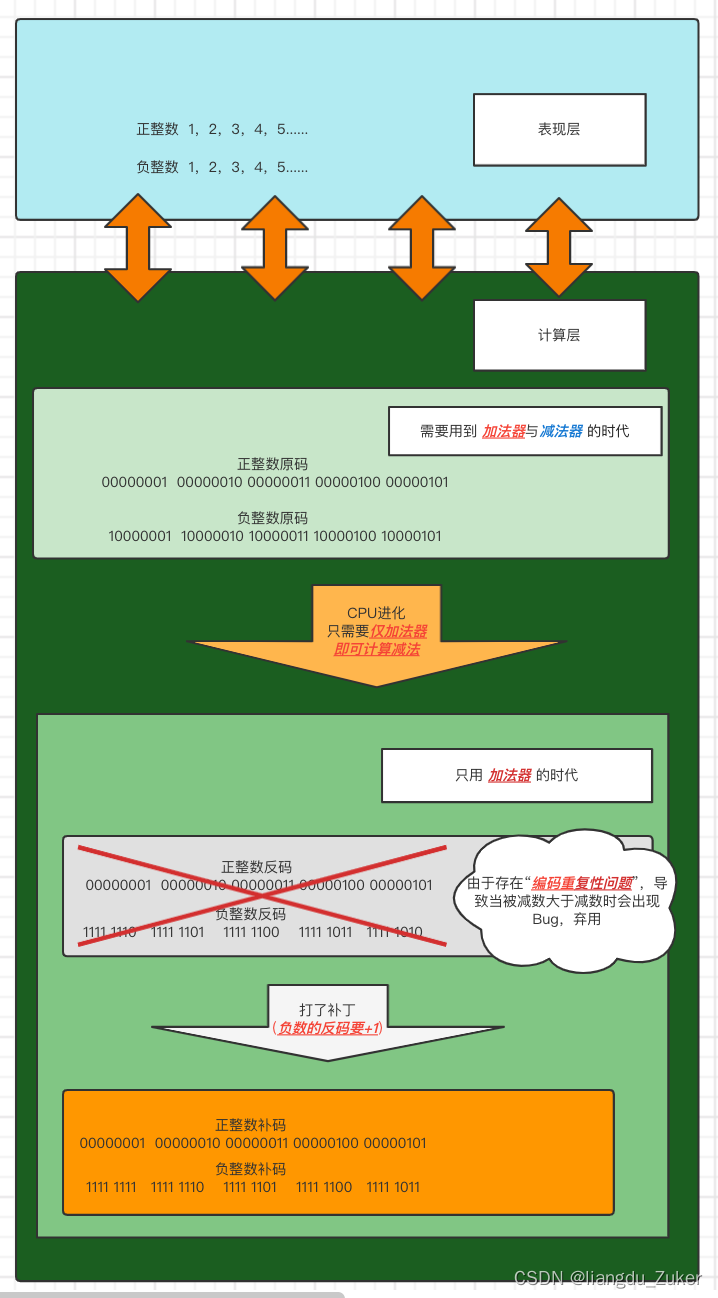
计算机，用二进制运算解决了 十进制数加减乘除的问题。

• 我们可以将其分为 “表示层” 和 “计算层”
• 其中计算层由 “加减法器时代” ，精简化为 “仅用加法器的时代”，也就是“原码” 进化到 “反补码” 的时代。
• 而由于 “反码” 存在 “编码重复问题” 被抛弃，升级为 “补码”。

演示反码的Bug

先说明，反码的Bug 是反码本身存在 “编码重复性” 问题所导致的（即存在多个 编码对应 1个值，类似人们身份证的重名。）

1.演示反码能正常工作的场景

（两正和两负数的场景不展开演示了，有兴趣可以自行研究“是否受编码重复性影响？”）：
-8 + 2 = -6
原码： 1000 1000 + 0000 0010 = 1000 0110
反码： 1111 0111 + 0000 0010 = 1111 1001 （原码 1000 0110 -6 ）
补码： 1111 1000 + 0000 0010 = 1111 1010 （原码 1000 0110 -6 ）

2. 演示反码不能正常工作的场景

8 - 2 = 6
原码： 0000 1000 + 1000 0010 = 0000 0110
反码： 0000 1000 + 1111 1101 = 0000 0101（原码 0000 0101 5 ）
补码： 0000 1000 + 1111 1110 = 0000 0110 （原码 0000 0110 6 ）
由于 溢出导致进位，而反码存在重复问题（原码的 0 可以用 0000 0000 表示，也可以用 1000 0000 表示，所以涉及到进位溢出时，会比预期值少 1）

3.演示反码不能正常工作的临界场景

3 - 2 = 1
原码： 0000 0011 + 1000 0010 = 0000 0110
反码： 0000 0011 + 1111 1101 = 0000 0000（原码 0000 0000 0 ）
补码： 0000 0011 + 1111 1110 = 0000 0001 （原码 0000 0001 1 ）

4. 演示反码碰巧能正常工作的临界场景

这个时候虽然也发生溢出进位，但由于结果刚好是 -0，负0也是0，所以侥幸命中正确值 0 。
2 - 2 = 0
原码： 0000 0010 + 1000 0010 = 0000 0110
反码： 0000 0010 + 1111 1101 = 1111 1111（原码 1000 0000 0 ）
补码： 0000 0010 + 1111 1110 = 0000 0000 （原码 0000 0000 0 ）

总结

• 我们可以理解反码的问题是“编码重复性”引起的（即存在多个 编码对应 1个值，类似人们身份证的重名。）

• 补码通过移动（反码+1）解决了这个问题，

• 补码的设计思路，个人理解，类似我们写算法处理边界问题时采用“哨兵模式”。

• 当然我觉得解决“编码重复性”问题的方法，还是有很多种的，比如 “ case by case ” 就是一种粗暴的手段。