系列文章目录

数据结构 —— 顺序表
数据结构 —— 单链表
数据结构 —— 双向链表

---

---

前言

数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。数据结构是一种十分优秀的解决实际问题的模板，是先进思想的结晶。博主将会用代码结合大量图解，对数据结构进行深度剖析，以便大家更好的学习数据结构的思想。

一、示例问题：酒店住宿

1.住宿需求

某公司需要一串连续的房间让员工住宿，但不清楚有多少员工将会入住

2.住宿管理

公司：首先安排了 3 个员工入住酒店

酒店：安排了 3 个连续房间 1 - 3 号房间

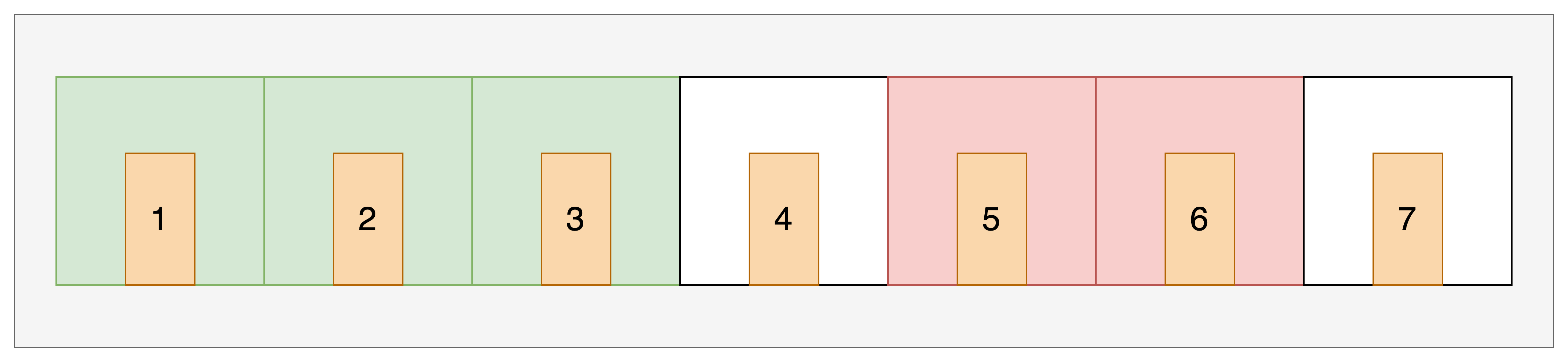
公司：又安排了 2 个员工入住

酒店：

1. 后面的 4 号房间空闲，但 5 号房有其他人入住，无法直接向后开辟房间
2. 重现寻找连续的 5 个房间

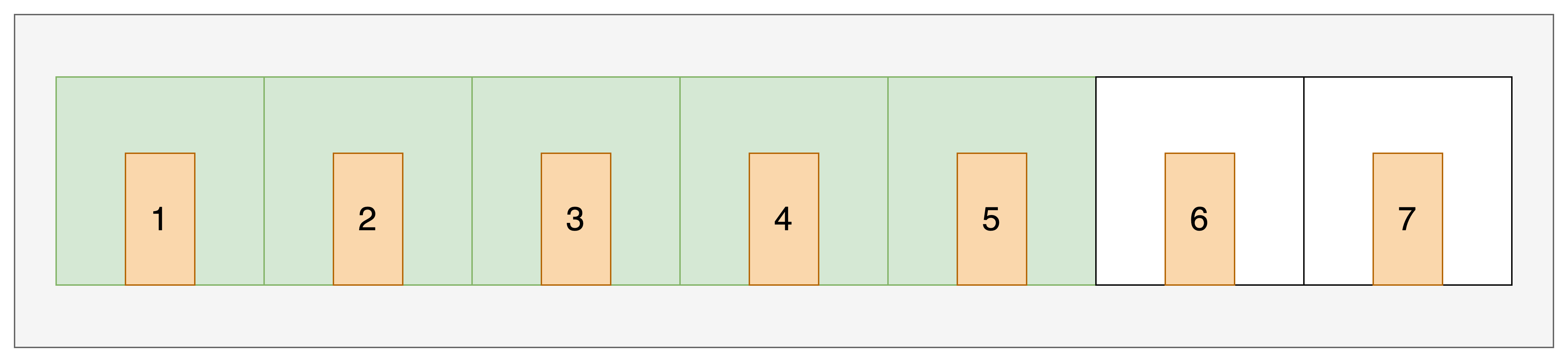
公司：又安排了 2 个员工入住

酒店：后面的 6 号和 7 号房间均空闲，直接向后面开辟两个房间

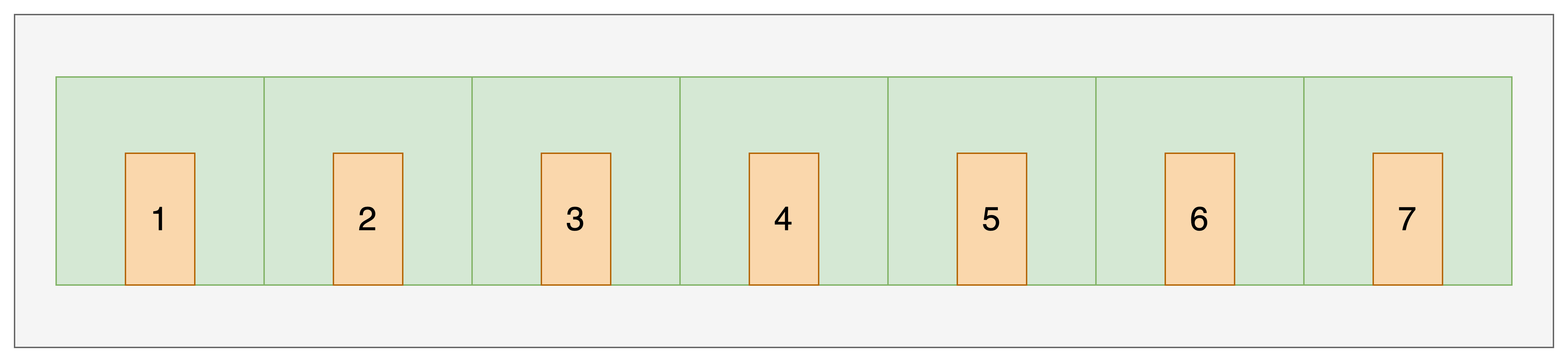
到此酒店成功满足了该公司的需求，通过这个示例问题引出了我们下面将要讲的顺序表，它们可以完美的描述并解决上述问题。

二、顺序表的概念

1.定义

顺序表：用一段地址连续的存储单元依此存储线性表的数据元素

顺序表就像是军训时，同学们站成一排，从左往右报数，每个人对应一个序号，这些序号是一个接着一个的有序排列。数组就是顺序表的一种，每个位置站着一名同学，他的序号就是数组的下标，通过序号就能找到那个同学。

2.结构

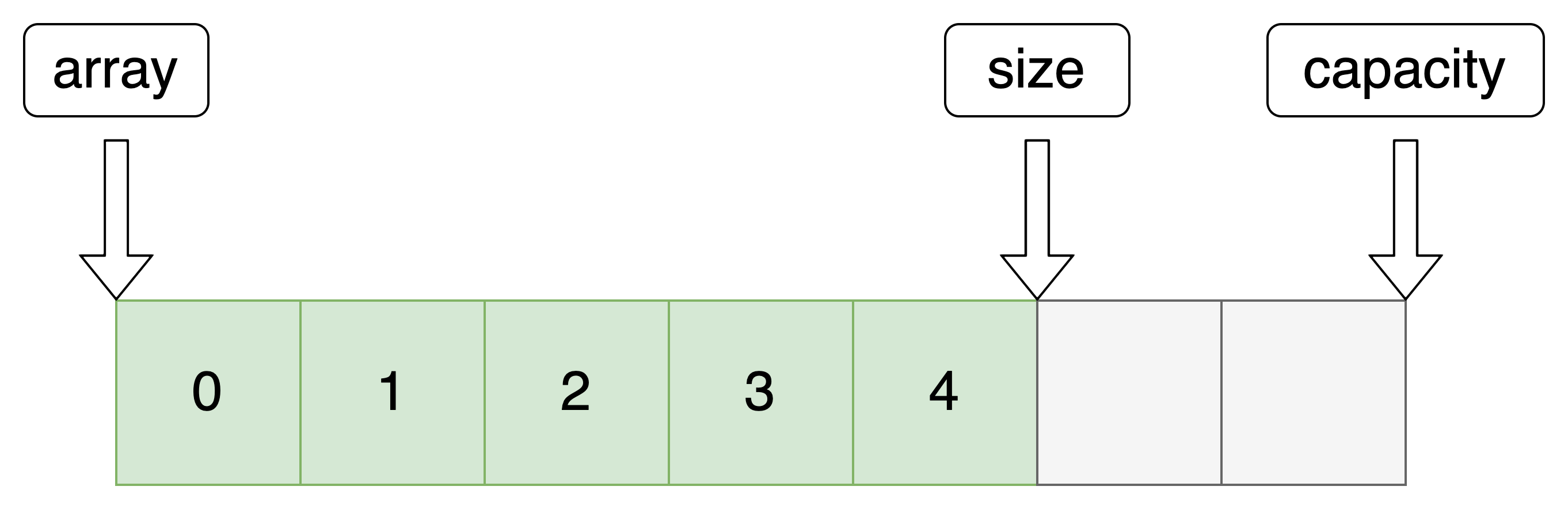
顺序表的结构类型

//重定义类型
typedef int SeqDateType;	//便于更改存储类型

//顺序表类型
typedef struct SeqList {
    SeqDateType *array;  	//顺序表
    int size;        		//有效数据的个数
    int capacity;    		//总容量
}SeqList;
1
2
3
4
5
6
7
8
9

3.存储

存储：用动态开辟的一维数组来实现顺序表的存储结构

三、顺序表的接口函数

1.初始化

对顺序表的内容进行初始设置

//初始化
void SeqListInit(SeqList *pq) {
    assert(pq);
    pq->array = NULL;				//指针置空
    pq->capacity = pq->size = 0;	//大小和容量赋值为0
}
1
2
3
4
5
6

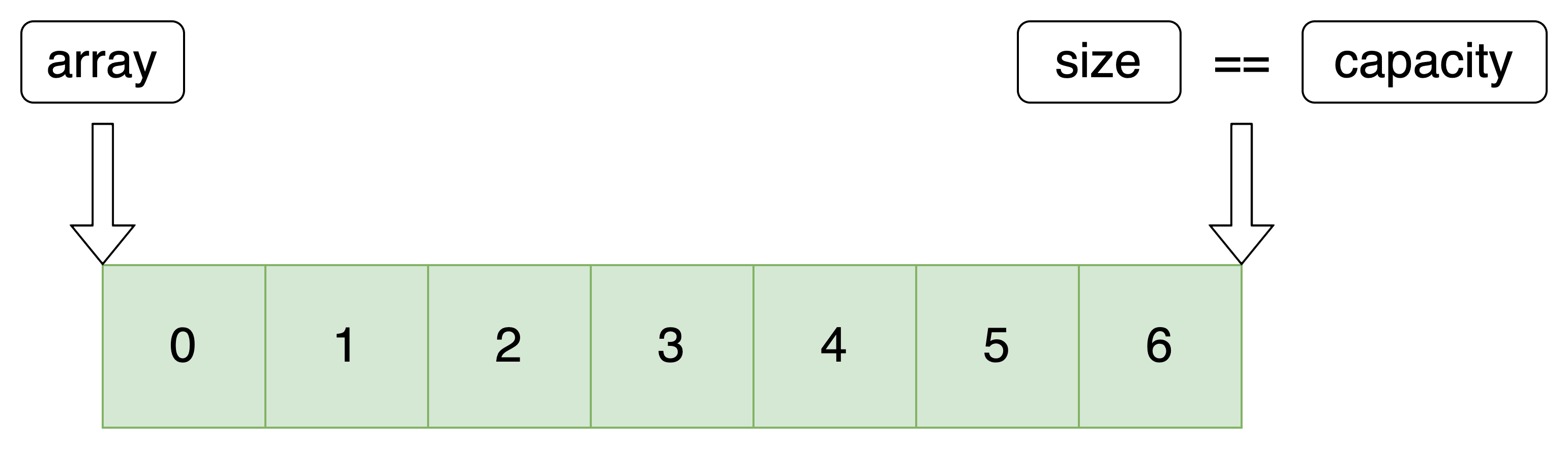
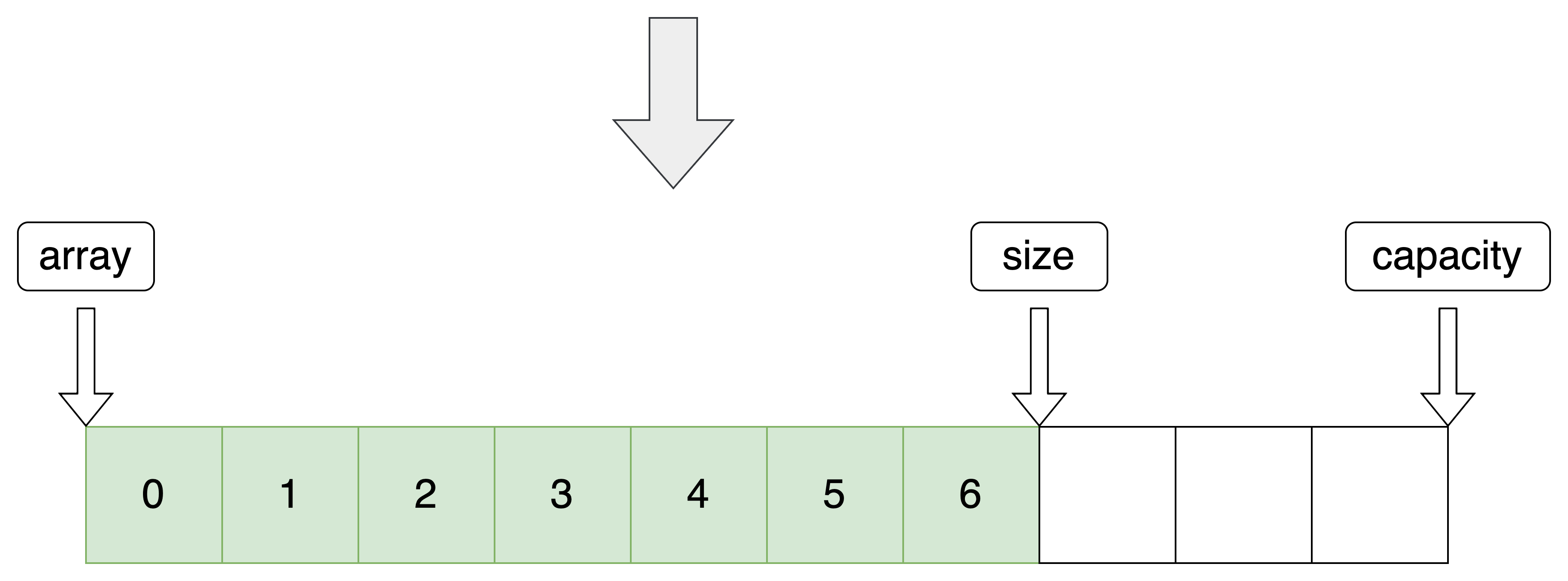
2.容量检查

判断是否达到最大容量

• 达到最大容量 —— 扩容
• 没有达到最大容量 —— 不扩容

//判断是否存满
void SeqCheckCapacity(SeqList *pq) {
    assert(pq);
    if (pq->size == pq->capacity) {
        int newcapacity = (pq->capacity == 0) ? 4 : (pq->capacity * 2);  //判断是否开辟空间 若没有自动开辟
        SeqDateType *newA = (SeqDateType *) realloc(pq->array, sizeof(SeqDateType) * newcapacity);
        if (newA == NULL) {
            perror("realloc fail:");
            exit(-1);
        }
        pq->array = newA;
        pq->capacity = newcapacity;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

达到最大容量 —— 扩容

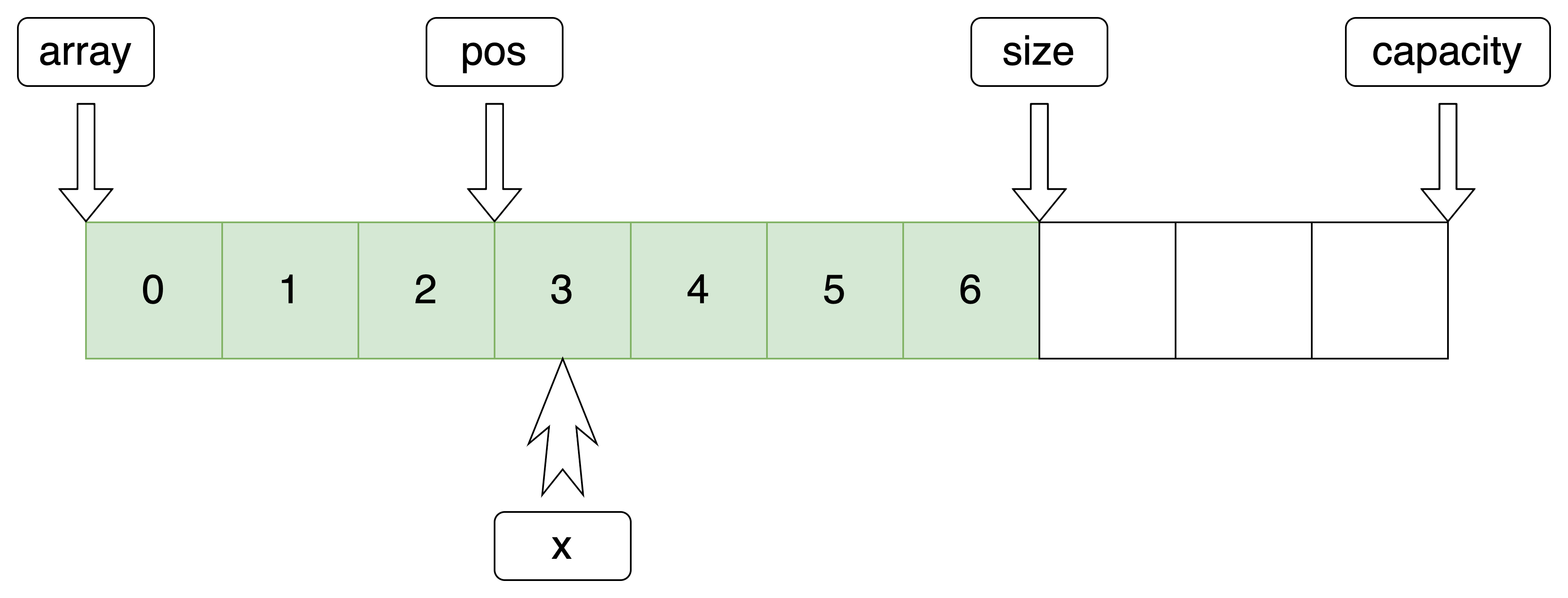
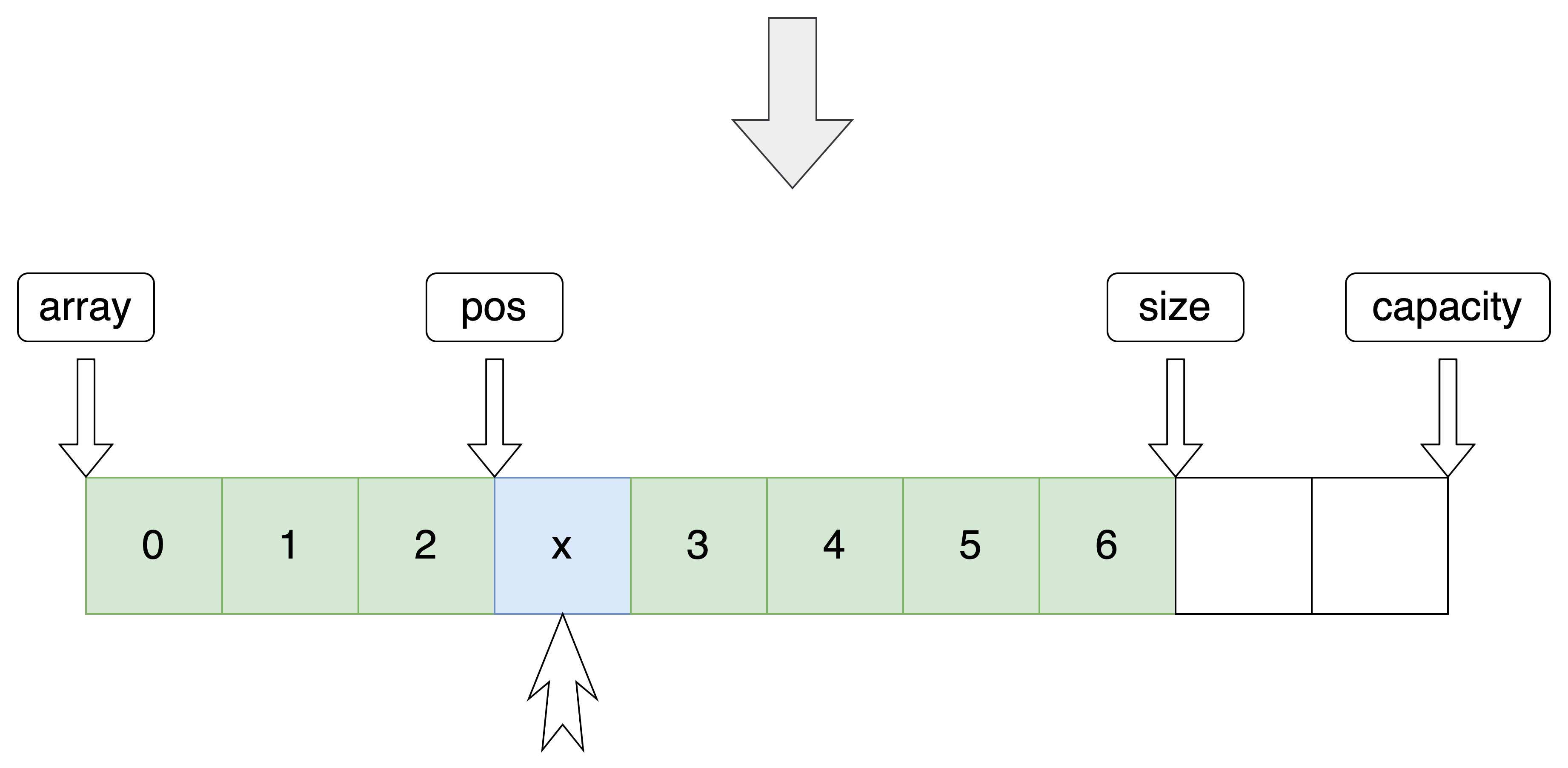
3.指定位置插入

指定位置 pos 插入数据

//指定位置插入
void SeqListInsert(SeqList *pq, int pos, SeqDateType x) {
    assert(pq);
    assert(pos >= 0 && pos <= pq->size);
    //判断扩容
    SeqCheckCapacity(pq);
    //向后推移
    int end = pq->size;
    while (end > pos) {
        pq->array[end] = pq->array[end - 1];
        end--;
    }
    pq->array[pos] = x;
    pq->size++;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

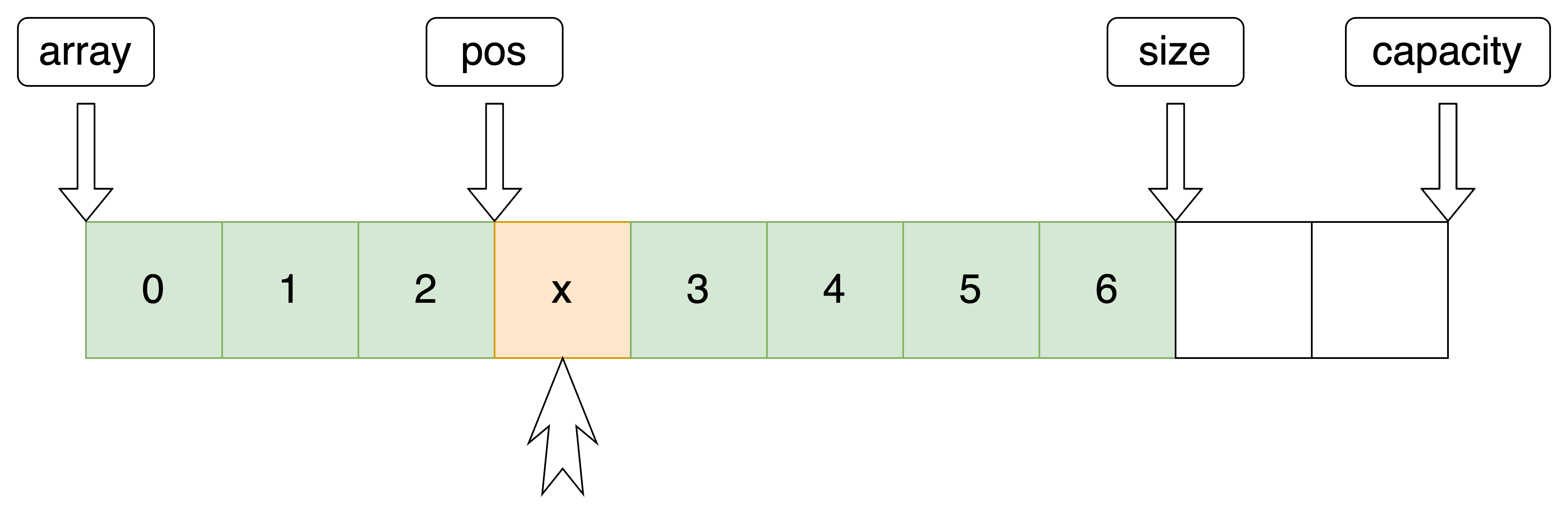
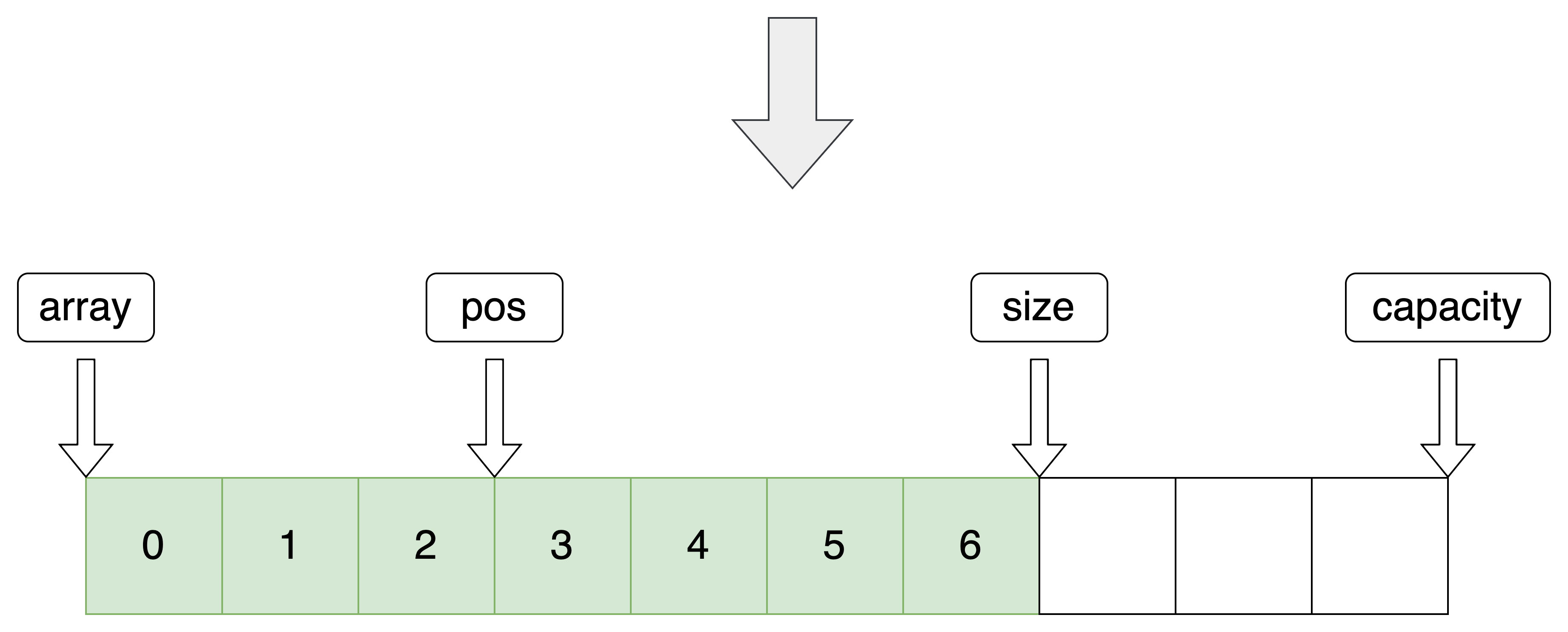
4.指定位置删除

删除指定位置 pos 的数据

//指定位置删除
void SeqListErase(SeqList *pq, int pos) {
    assert(pq);
    assert(pos < pq->size);
    //向前推移
    for (int i = pos + 1; i < pq->size; i++) {
        pq->array[i - 1] = pq->array[i];
    }
    pq->size--;
}
1
2
3
4
5
6
7
8
9
10

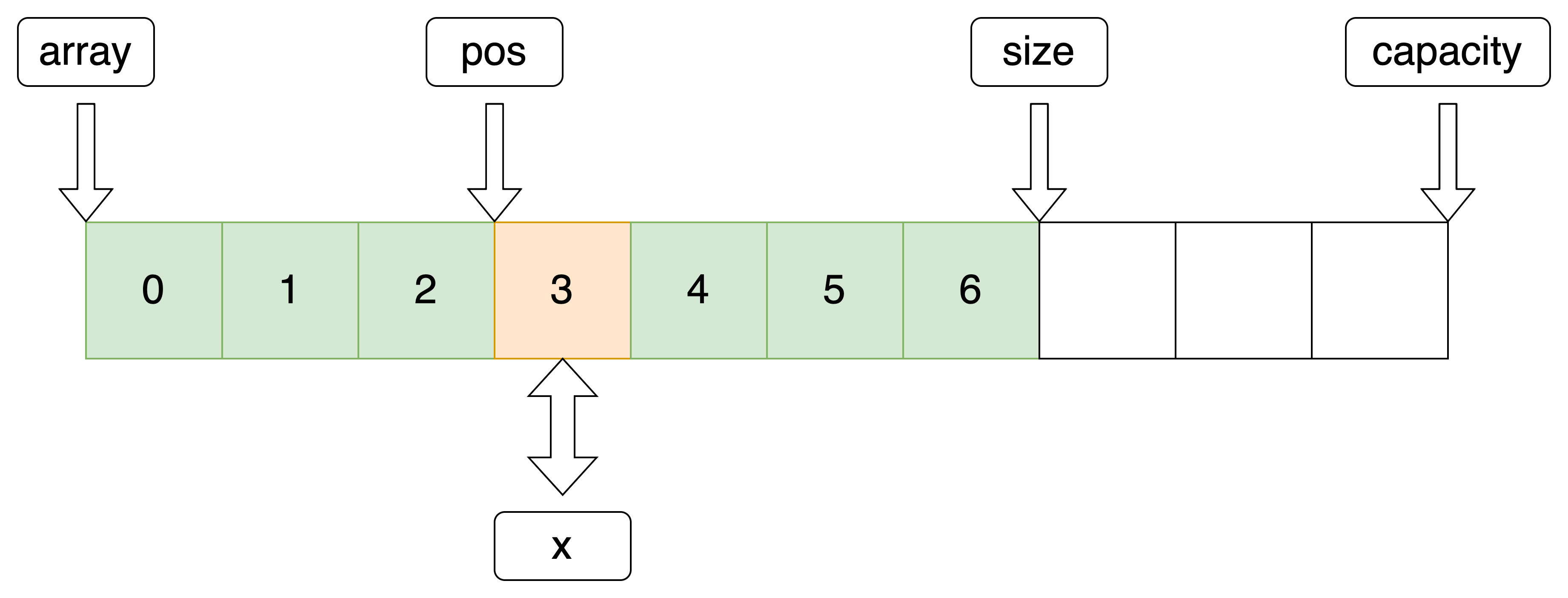
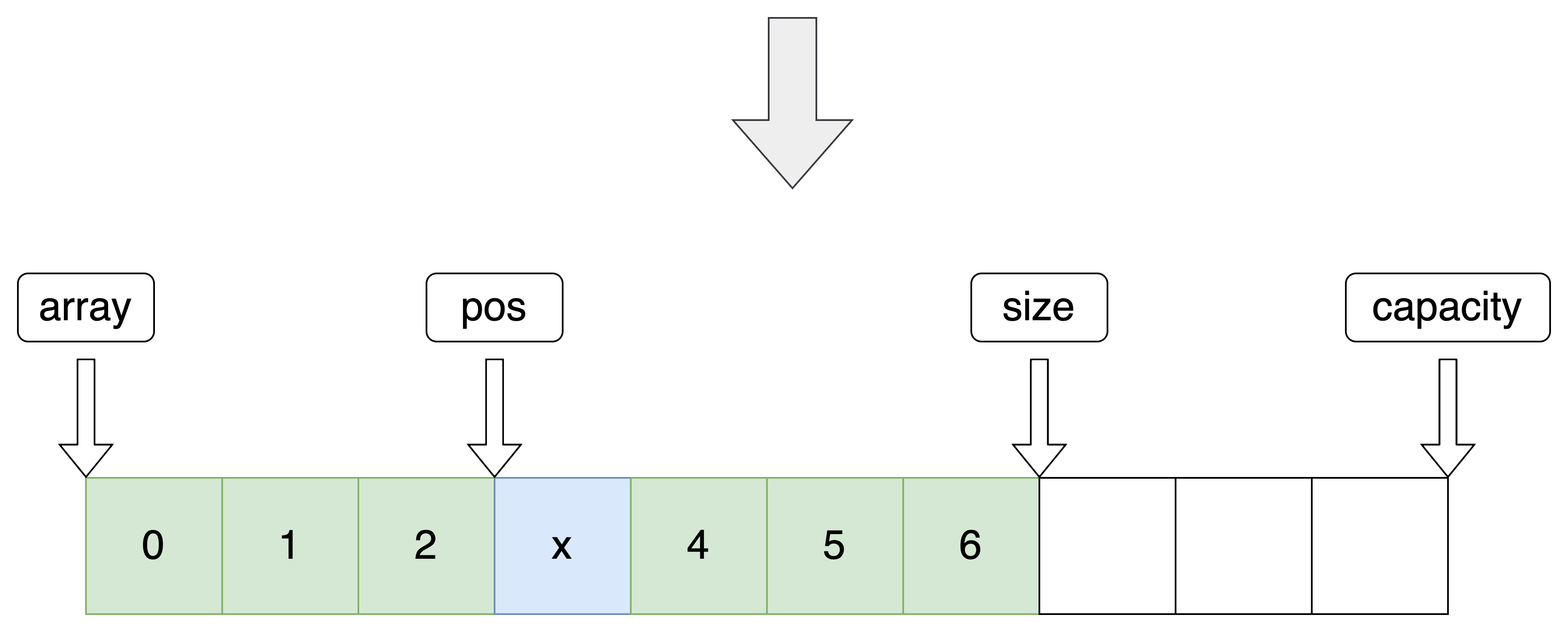
5.指定位置修改

修改指定位置 pos 的数据

//修改数据
void SeqListModify(SeqList *pq, int pos, SeqDateType x) {
    assert(pq);
    assert(pos >= 0 && pos < pq->size);
    pq->array[pos] = x;
}
1
2
3
4
5
6

6.查找数据

查找指定数据

• 存在 —— 返回第一次查找到的位置
• 不存在 —— 返回 NULL

//查找数据
int SeqListFind(SeqList *pq, SeqDateType x) {
    assert(pq);
    //查找数据
    for (int i = 0; i < pq->size; i++) {
        if (pq->array[i] == x) {         //如果找到了返回位置
            return i;
        }
    }
    return -1;                         //如果没找到返回-1
}
1
2
3
4
5
6
7
8
9
10
11

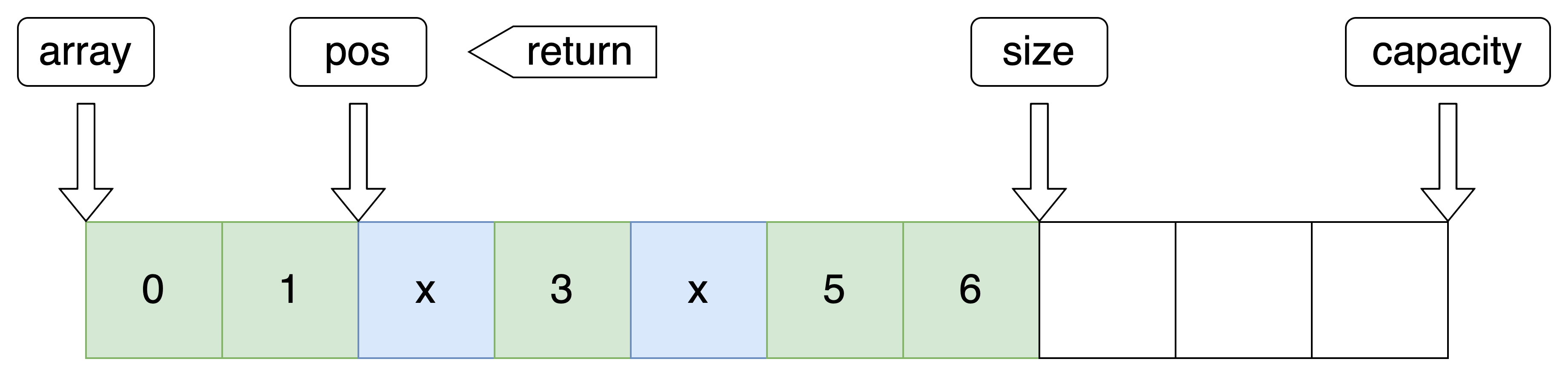
7.头部插入

利用指定位置插入实现头插

//头部插入
void SeqListPushFront(SeqList *pq, SeqDateType x) {
    SeqListInsert(pq, 0, x);
}
1
2
3
4

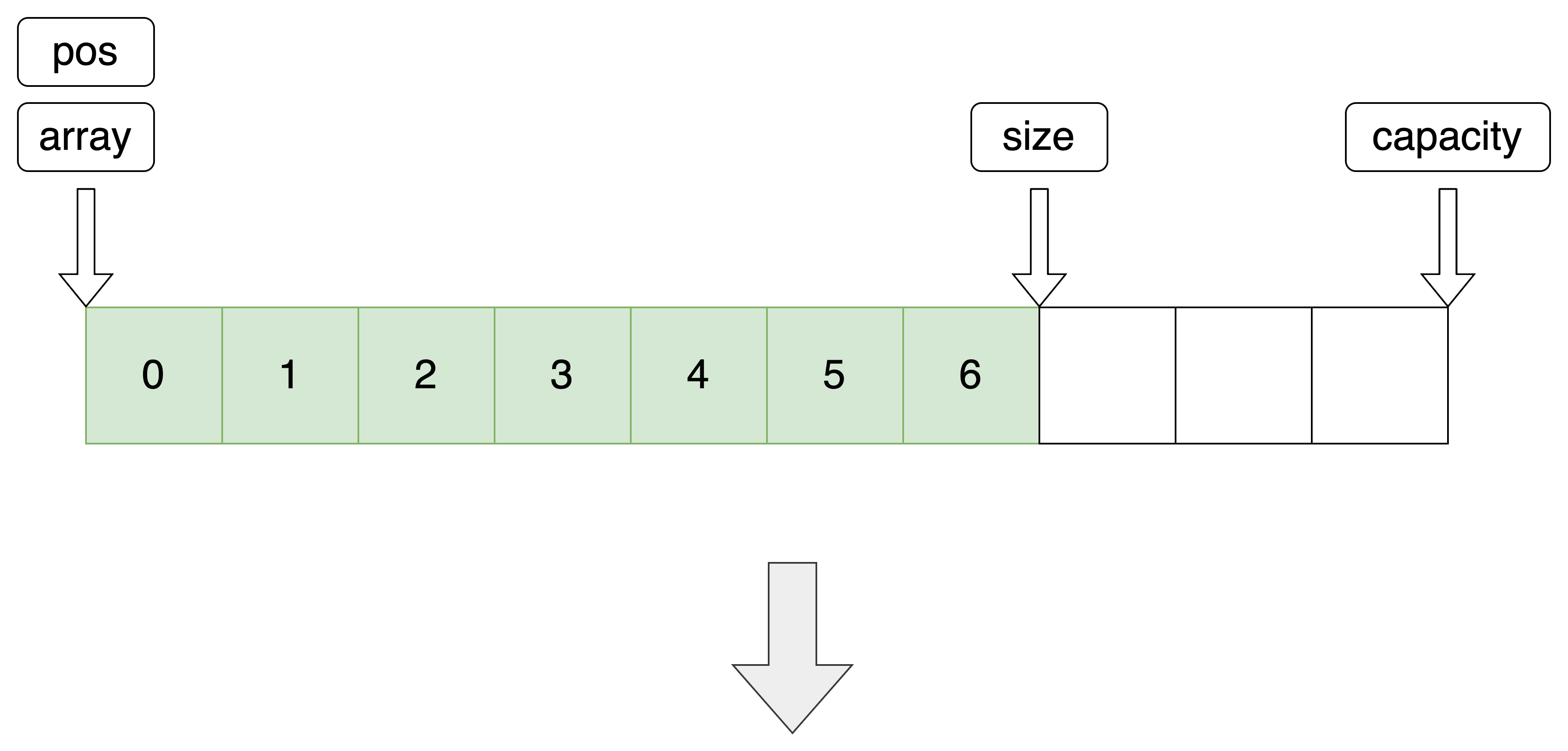
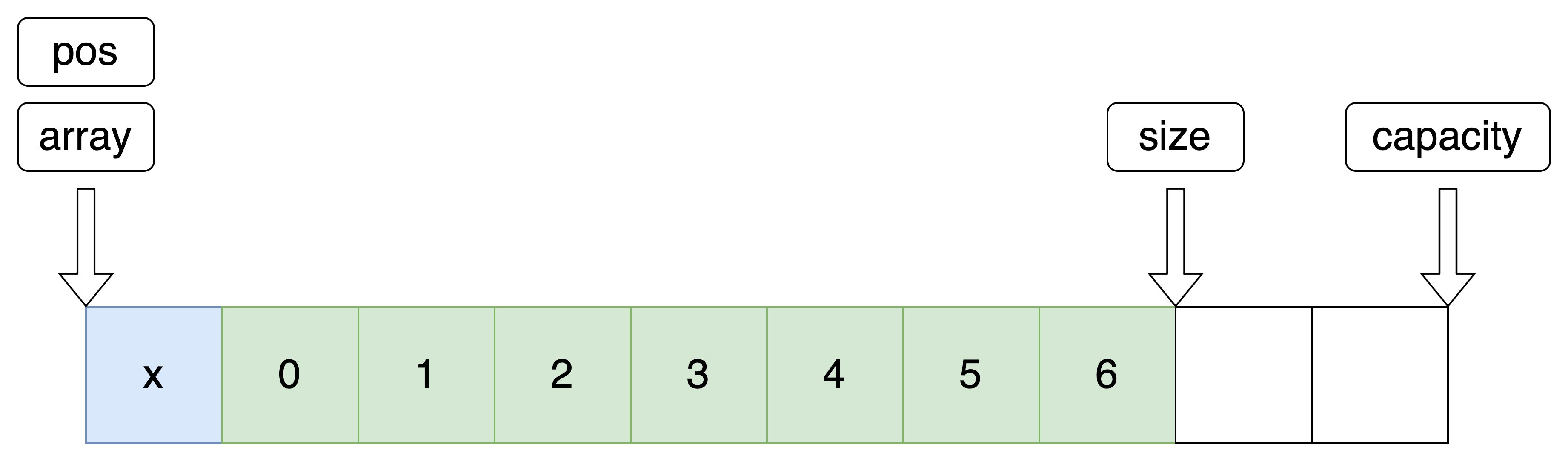
8.头部删除

利用指定位置删除实现头删

//头部删除
void SeqListPopFront(SeqList *pq) {
    SeqListErase(pq, 0);
}
1
2
3
4

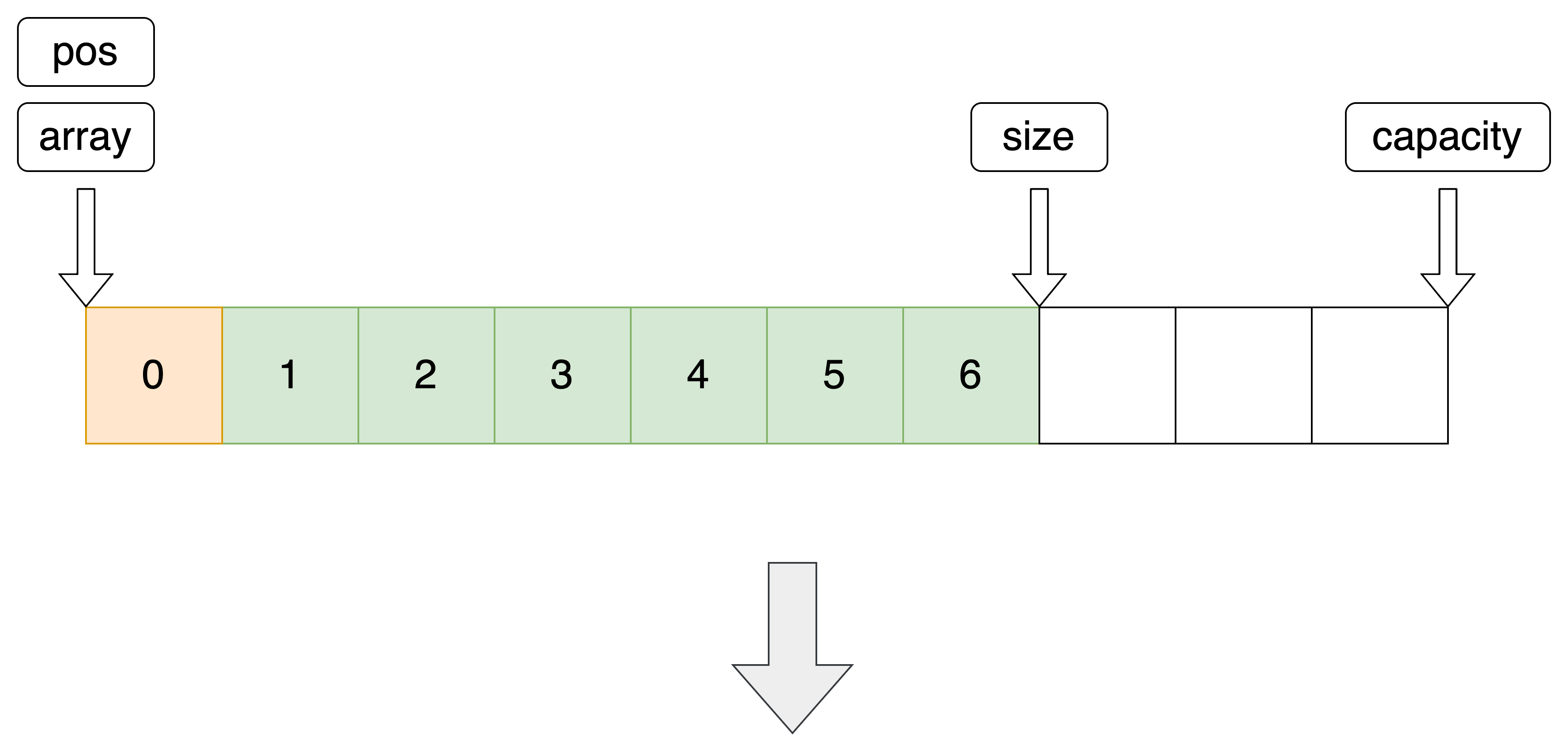
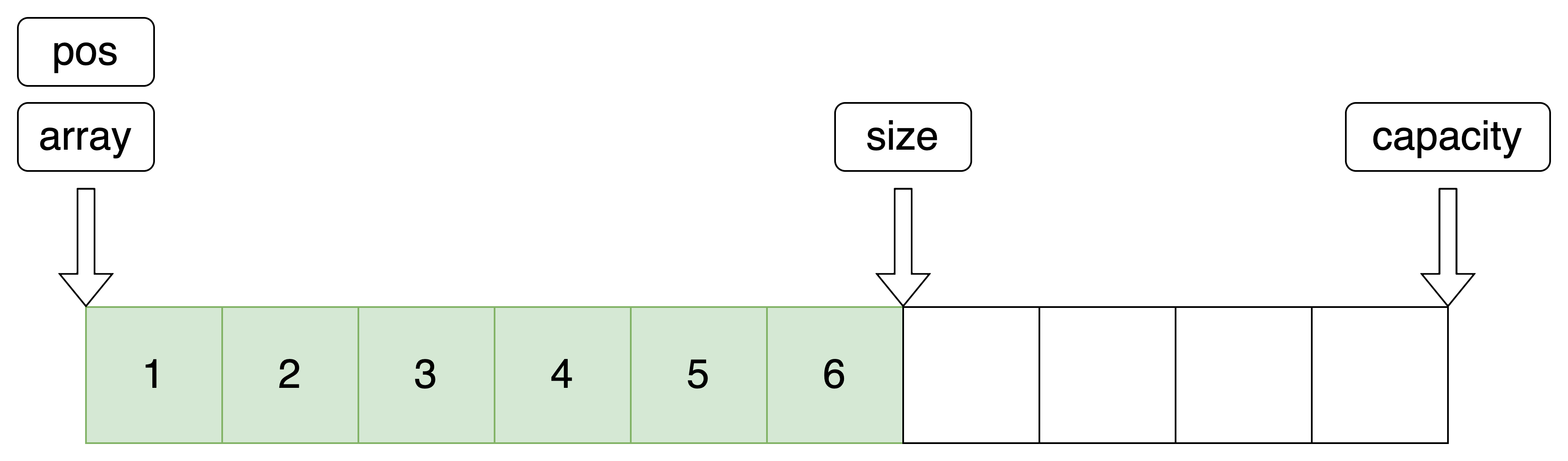
9.尾部插入

利用指定位置插入实现尾插

//尾部插入
void SeqListPushBack(SeqList *pq, SeqDateType x) {
    SeqListInsert(pq, pq->size, x);
}
1
2
3
4

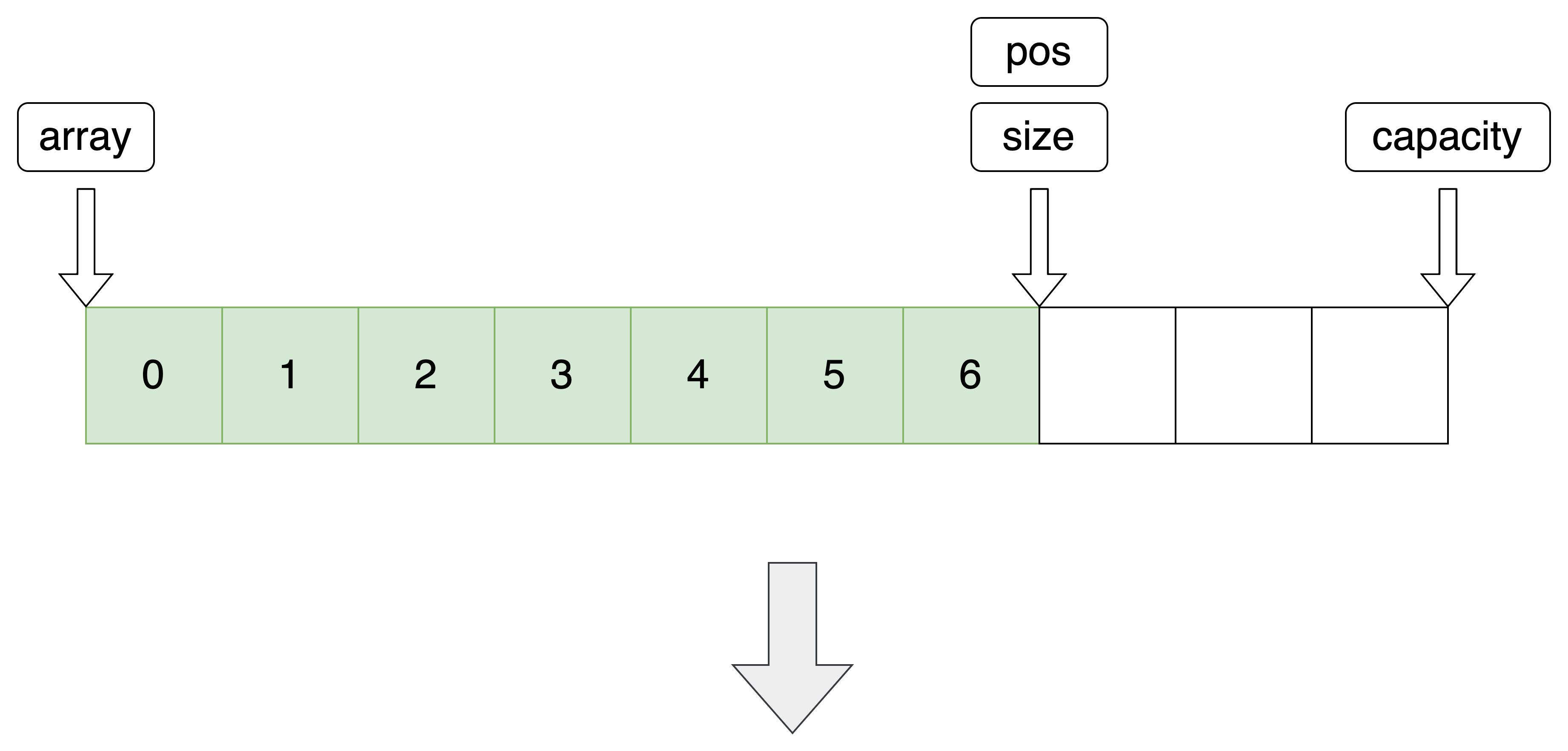
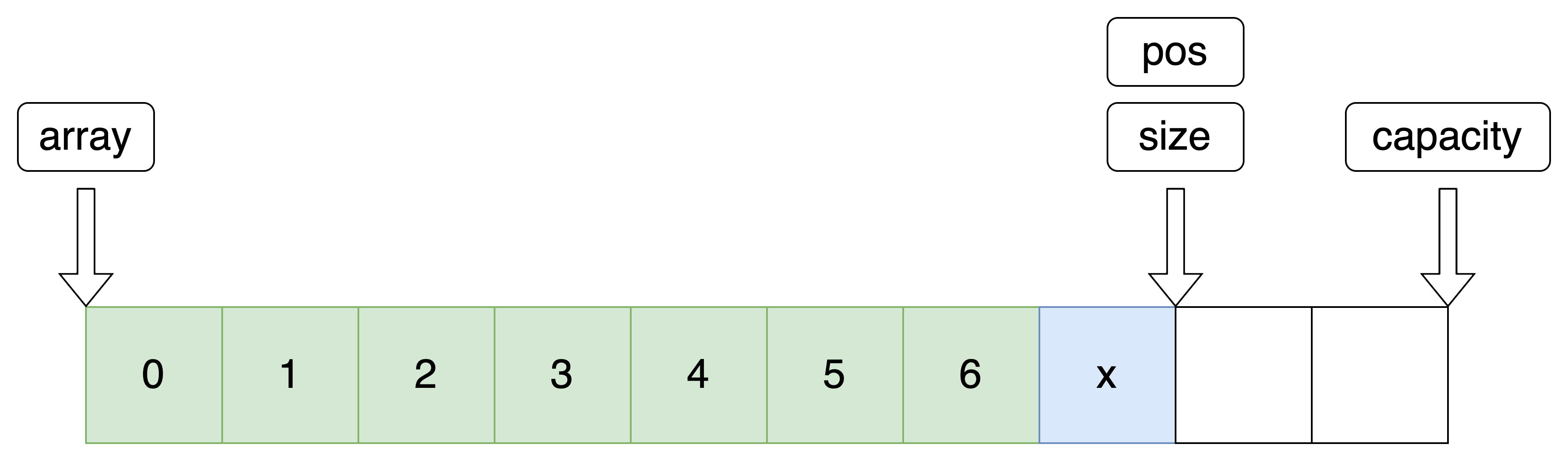
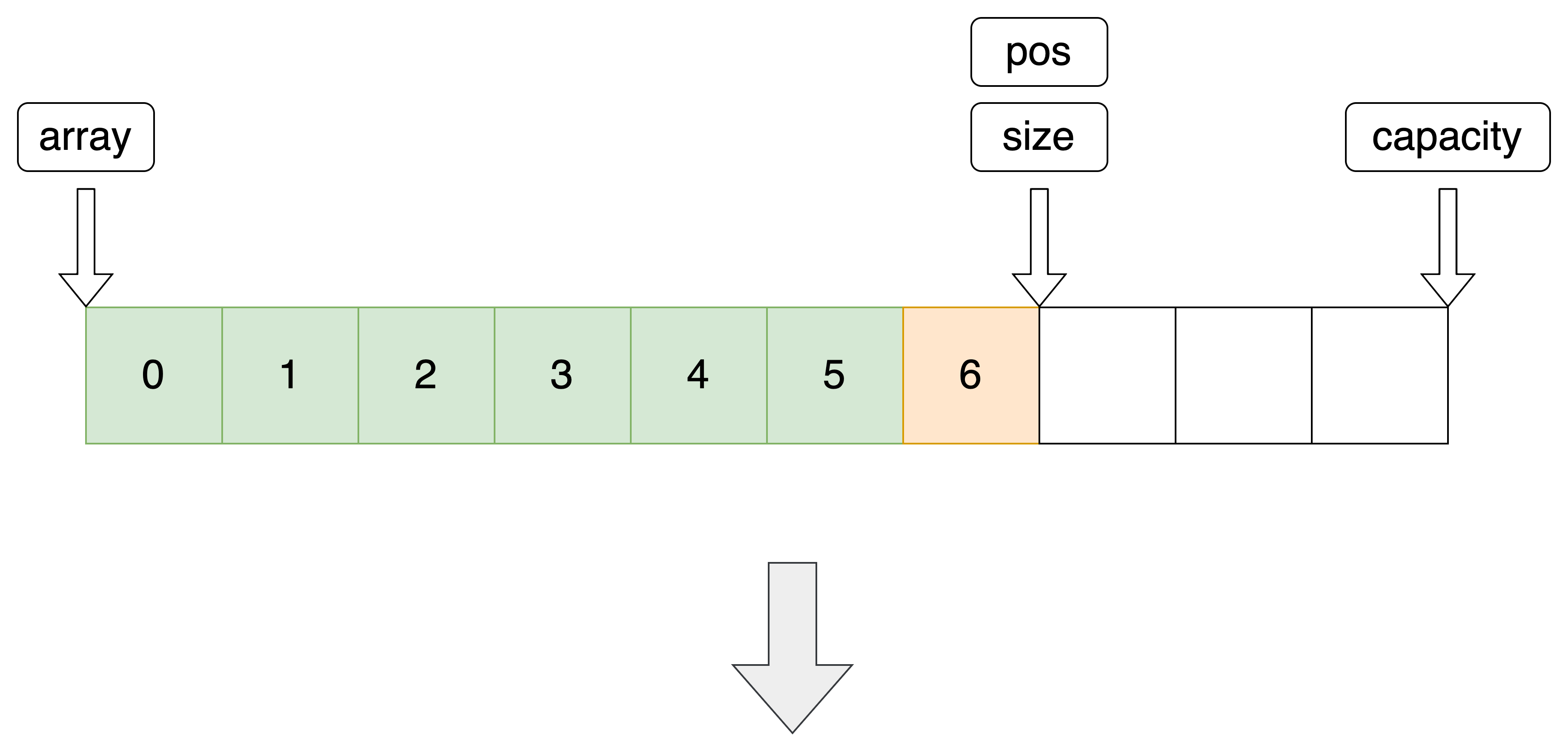
10.尾部删除

利用指定位置删除实现尾删

//尾部删除
void SeqListPopBack(SeqList *pq) {
    SeqListErase(pq, pq->size - 1);
}
1
2
3
4

---

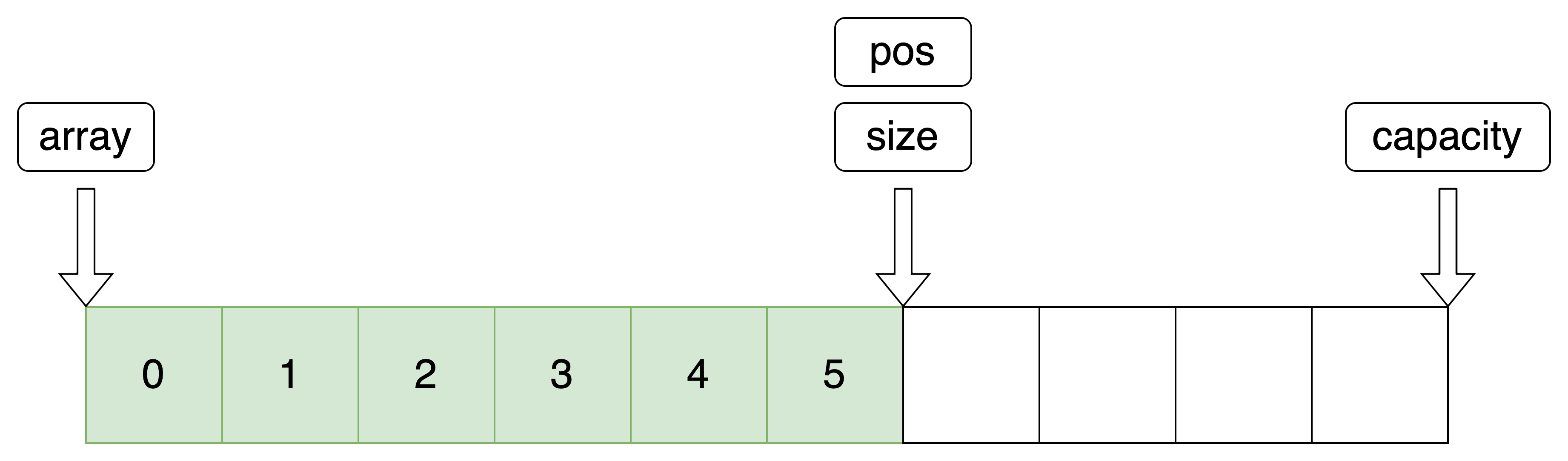
四、总结

顺序表是解决实际问题时极其常用的一种数据结构，是非常重要的解决问题的方式。顺序表的各种接口的复现，有利于更好的学习数据结构的思想，有利于开阔视野，学习前辈的智慧结晶。对我们后续解决实际问题也会有很大帮助。