-
算法分析与设计:CH7快排详解(文末附快排完整算法)
CH7:QuickSort
7.1 Description of QuickSort
7.1.1 Randomized algorithm
随机的应用:
QuickSort
rand():产生0~1之间随机数
为什么使用随机?——没有更好的解决方法
7.1.2 快排的概述
分治的结果:分解时做得少,那么合并时就要做的多。反之,分解时做得多,那么合并时做得少。
Divide:利用pivot将数组分为两半,一半比pivot大,一半比pivot小
Conquer:递归求解子数组
Combine:Trival
7.1.2.1 Divide and Conquer
(1)QuickSort
主算法:
quickSort(A, p, r)主要做分治,分解问题时做较多的石墙:每次确定pivot的位置
pivot位置确定后,分别递归求解左边和右边的数组
算法为原地排序,不需要合并
void quickSort(vector<int>& vec, int start, int end) { if (start < end) { // 分 int pivot_index = partition(vec, start, end); // 治 quickSort(vec, start, pivot_index-1); quickSort(vec, pivot_index+1, end); // 原地排序,不需要合并 } }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
(2)Partition
注意
i的初始化注意各个区间的表示含义:
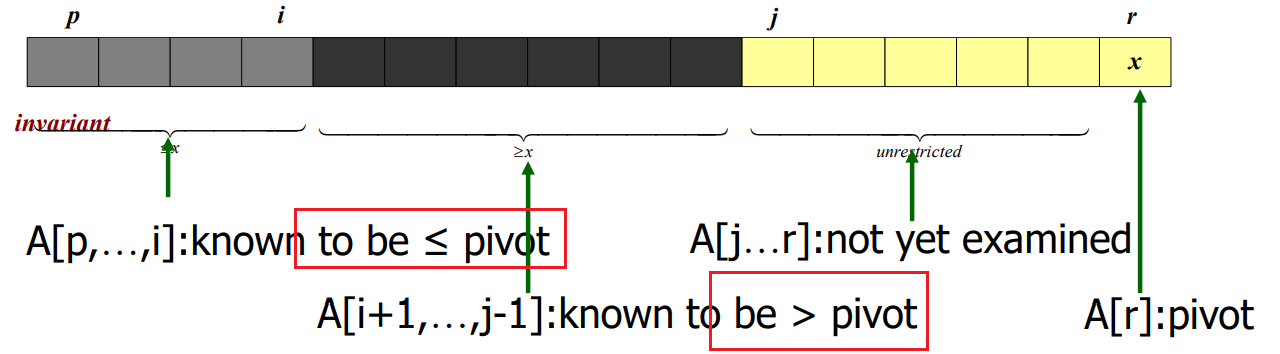
程序如下:
int partition(vector<int>& vec, int start, int end) { // pivot的选择 int pivot = vec[end]; // 选择最后一个元素充当pivot int i = start - 1; for (int j = start; j <= end; j++) { if (vec[j] <= pivot) { i++; int temp = vec[i]; // 一个比pivot大的数 vec[i] = vec[j]; // 和找到的小于等于pivot的数交换 vec[j] = temp; } } return i; }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
有多少个比pivot小的,那么就加几次1
7.1.2.2 快排的分析
假设每个元素是不一样的,现实中,如果有重复的元素,那么有更好的算法存在。
(1)快排的最坏情况
我们假设 T ( n ) T(n) T(n)是最坏情况下的运行时间,那么:
最坏情况发生在pivot是最大或者最小的元素时,此时,问题分解成两个问题,其中一个问题的规模为0,另一个问题的规模为n-1。
一次只会减少规模1.
T ( n ) = T ( n − 1 ) + T ( 0 ) + Θ ( n ) T(n) = T(n-1) + T(0) +\Theta(n) T(n)=T(n−1)+T(0)+Θ(n)
递归树如下: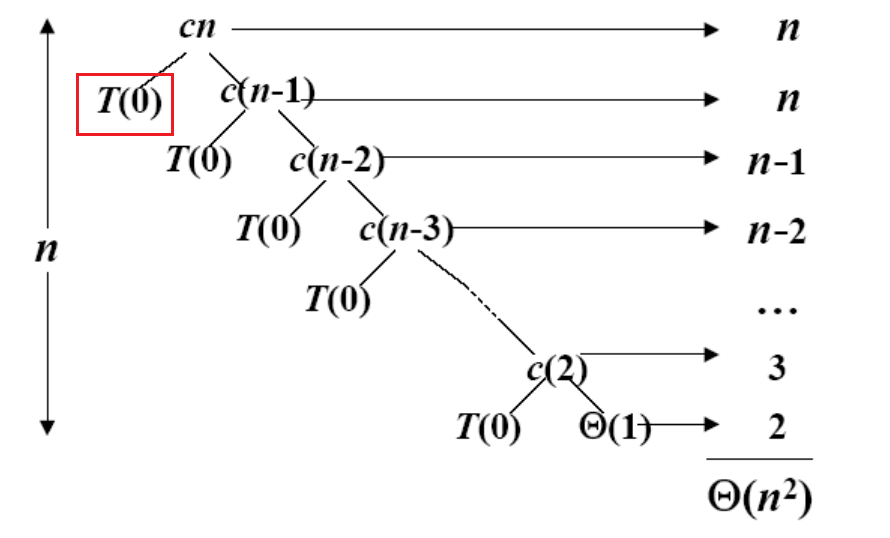
(2)快排的最好情况
快排的最好情况发生在每次选取的pivot为中位数时,
T ( n ) = 2 T ( n / 2 ) + Θ ( n ) T(n) = 2T(n/2) +\Theta(n) T(n)=2T(n/2)+Θ(n)
此时,递归树如下: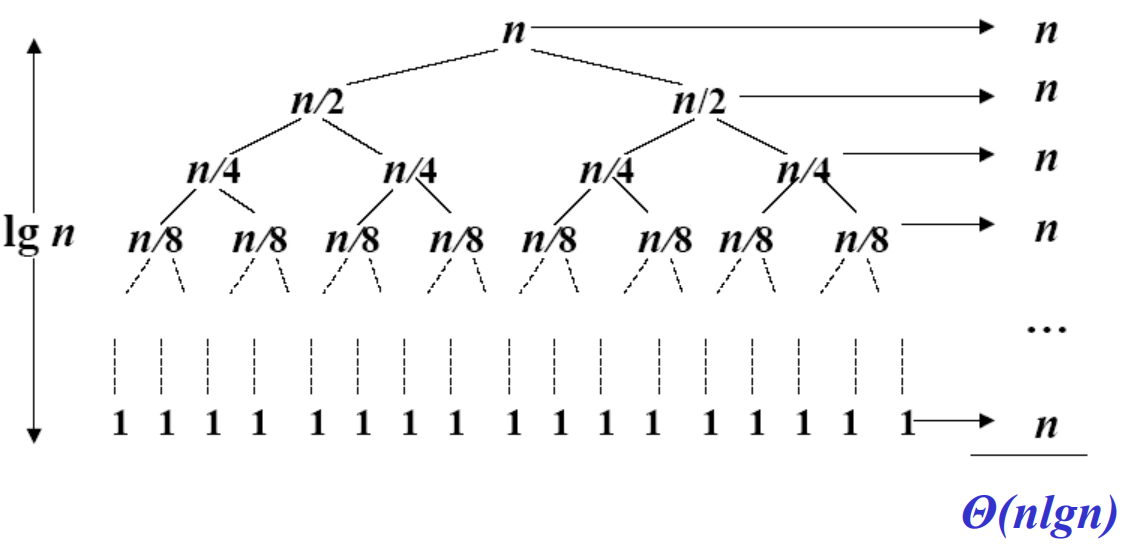
时间复杂度与归并相同。
(3)1:9情况
假设pivot每次把数组分为1:9的两个数组,那么递归式如下:
T ( n ) = T ( 9 n / 10 ) + T ( n / 10 ) + Θ ( n ) T(n) = T(9n/10)+T(n/10) +\Theta(n) T(n)=T(9n/10)+T(n/10)+Θ(n)
此时的递归树如下: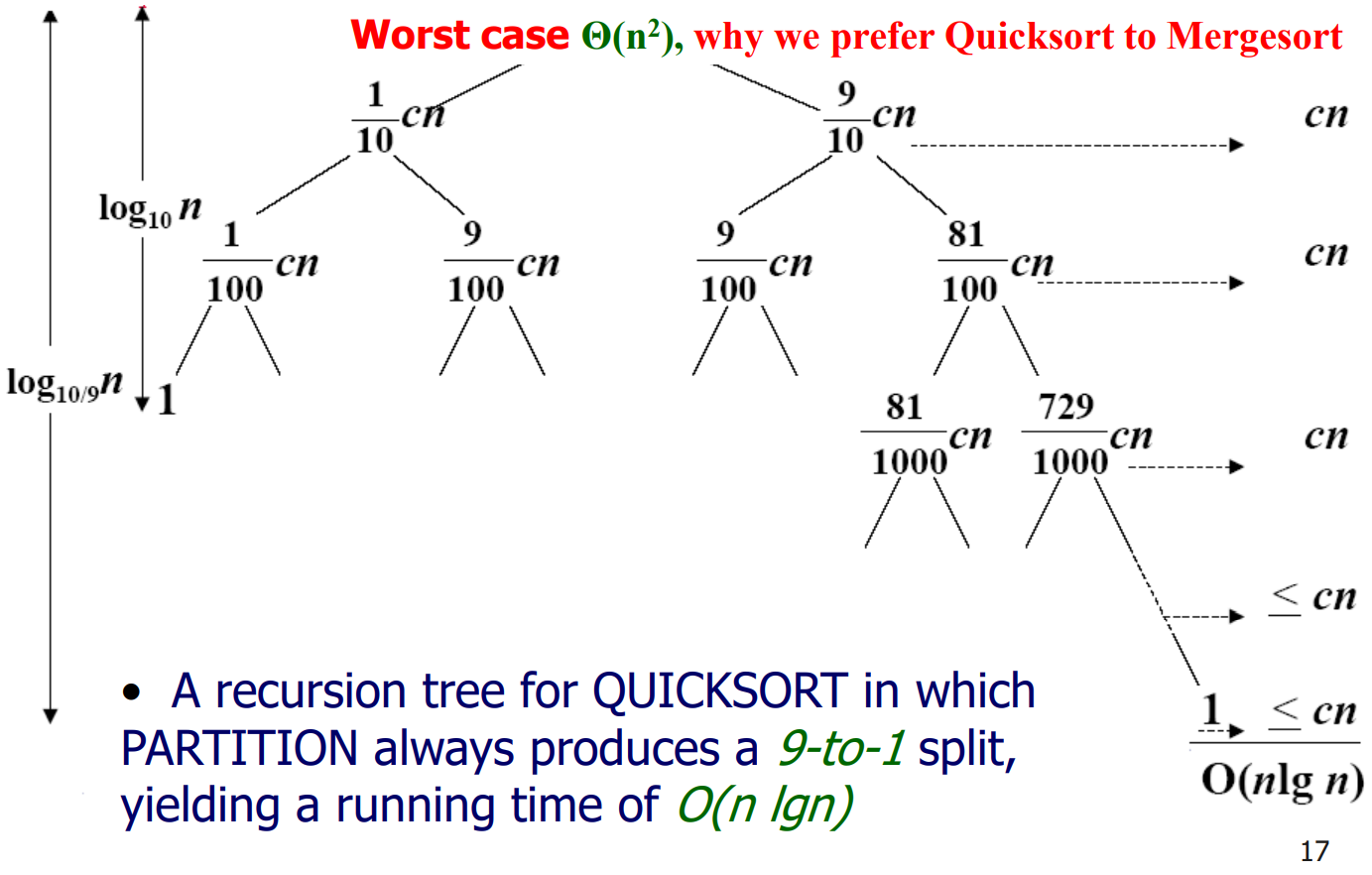
每次都除以 9 / 10 9/10 9/10,那么树高为 l o g 10 9 n log_{\frac{10}{9}}^{n} log910n
总代价小于 c n l o g 10 9 n cnlog_{\frac{10}{9}}^{n} cnlog910n,所以时间复杂度 T ( n ) = O ( n l g n ) T(n) = O(nlgn) T(n)=O(nlgn)
(4)引入随机的快排
随机选择一个元素作为Pivot。
// 引入随机 int RandomizedPartition(vector<int>& vec, int start, int end) { int p = rand() % (end - start + 1) + start; // 随机选择一个作为pivot int temp = vec[p]; vec[p] = vec[end]; vec[end] = temp; return partition(vec, start, end); }- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
每次都选到最大或者最小的数的概率为:
2 100 × 2 99 . . . . . . . × 2 2 \frac{2}{100}\times\frac{2}{99}.......\times \frac{2}{2} 1002×992.......×22
excepted time 为 O ( n l g n ) O(nlgn) O(nlgn)
快排完整算法:
#include#include #include using namespace std; int partition(vector<int>& vec, int start, int end) { // pivot的选择 int pivot = vec[end]; // 选择最后一个元素充当pivot int i = start - 1; for (int j = start; j <= end; j++) { if (vec[j] <= pivot) { i++; int temp = vec[i]; // 一个比pivot大的数 vec[i] = vec[j]; // 和找到的小于等于pivot的数交换 vec[j] = temp; } } return i; } // 引入随机 int RandomizedPartition(vector<int>& vec, int start, int end) { int p = rand() % (end - start + 1) + start; int temp = vec[p]; vec[p] = vec[end]; vec[end] = temp; return partition(vec, start, end); } void quickSort(vector<int>& vec, int start, int end) { if (start < end) { // 分 int pivot_index = RandomizedPartition(vec, start, end); // 治 quickSort(vec, start, pivot_index-1); quickSort(vec, pivot_index+1, end); // 原地排序,不需要合并 } } void printVec(vector<int>& vec) { for(int i = 0; i < vec.size(); i++) { cout << vec[i] << " "; } cout << "\n" <<endl; } int main() { vector<int> vec = {3,6,1,7,-1,8,2,4,9,10,5,0}; quickSort(vec, 0, vec.size()-1); printVec(vec); return 0; } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
-
相关阅读:
胶囊网络深入理解
京准电钟 NTP时间同步服务器助力水库水坝水利自动化建设
浏览器无痕模式有什么作用,手机浏览器开启无痕模式的方法
仿游戏热血江湖游戏类22(FLD_FJ_中级附魂)
IP 地址冲突检测工具
使用ffmpeg解码video模块,支持3种解码:cpu解码、amd64平台的cuda解码和NX平台的Nvmpi解码
Unity小技巧 - 绘制瞄准准心
利用 API 接口进行自动代码生成的最佳实践
Linux系统防火墙iptables
Win11没有画图工具怎么重新安装
- 原文地址:https://blog.csdn.net/weixin_45745854/article/details/126166376
