第一节 栈在括号匹配中的应用

一、分析过程

1. 根据分析可以得到一下几个规律：

• 后面出现的左括号最先被匹配，遵循栈的LIFO特性
• 每出现一个右括号就要消耗一个左括号
• 遇到左括号就入栈，遇到右括号就消耗左括号
• 匹配不成功有三种情况：① 括号形状不匹配 ② 栈空了，但是仍然有右括号需要匹配 ③数组已经结束，但是栈内仍然有左括号（不空）

2. 设计算法过程：
   ① 初始设置一个空栈，顺序读入括号
   ② 若有右括号，就将置于栈顶的括号取出，匹配成功或者不合法
   ③若是左括号，那么就进行入栈操作
   ④ 输入结束时检查栈空，若为空，则匹配成功，反之不成功

二、算法实现

#include 
#include 
#include 
#define MaxSize 10
using namespace std;


typedef struct {
   char data[MaxSize];
   int top;
}SqStack;
//初始化栈
void IniStack(SqStack &s)
{
    s.top=0;
}
//判断栈是否为空
bool StaxkEmpty(SqStack s){
   if(s.top==0)
    return true;
   else
    return false;
}
//新元素入栈
bool Push(SqStack &s,char &x){
    s.data[s.top]=x;
    s.top++;
    return true;
}
//栈顶元素出栈，用x返回
bool Pop(SqStack &s,char &x){
    x=s.data[s.top-1];
    s.top--;
}
//匹配算法
bool bracketCheck(char str[],int length){
     SqStack s;
     IniStack(s);
     for(int i=0;i<length;i++){
        if(str[i]=='('||str[i]=='{'||str[i]=='['){
            Push(s,str[i]); //如果是左括号，入栈
           }
        else{
            if(StaxkEmpty(s))//如果是右括号并且栈为空
             return false;
           char topELem;
           Pop(s,topELem);
      
           if(str[i]==')'&&topELem!='(')
            return false;
           if(str[i]=='}'&&topELem!='{')
            return false;
           if(str[i]==']'&&topELem!='[')
            return false;
        }
       }
       return StaxkEmpty(s);
}
int main()
{    char str[MaxSize];
     int n;
     scanf("%s",str);
     scanf("%d",&n);
    if(bracketCheck(str,n))
        printf("匹配成功");
    else
        printf("匹配失败");
    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70

第二节 栈在表达式求值中的应用

1. 示例

一、中缀表达式转后缀表达式

（一） 改方法

1. 手写利用后缀表达式的方法
   ① 确定中缀表达式各个运算符的运算顺序
   ② 选择下一个运算符，按照**[左操作数 右操作数 运算符]**的方式组合成一个新的操作数
   ③ 如果还有运算符没有处理，就继续②
2. 后缀前缀都有可能不同,并且所有的操作数必须按照顺序
3. 选择“左优先”原则
   例子 A+B-CD/E+F 后缀： AB+CDE/-F+
4. 机改写方法
   初始化一个栈，用于保存暂时还不能确定运算顺序的运算符。从左到右处理各个元素，直到末尾。可能遇到三种情况：
   ① 遇到操作数。直接加入后缀表达式。
   ② 遇到界限符。遇到“(”直接入栈;遇到“)”则依次弹出栈内运算符并加入后缀表达式，直到 弹出“(”为止。注意:“(”不加入后缀表达式。
   ③ 遇到运算符。依次弹出栈中优先级高于或等于当前运算符的所有运算符，并加入后缀表达式， 若碰到“(” 或栈空则停止。之后再把当前运算符入栈。 按上述方法处理完所有字符后，将栈中剩余运算符依次弹出，并加入后缀表达式。
5. 机算实例
   

（二）计算方法

1. 手算
   从左往右扫描，每遇到一个运算符，就让运算符前面最近的两个操作数执行对应运算，合体为一个操作数
2. 机算
   ① 从左往右扫描下一个元素，直到处理完所有元素
   ② 若扫描到操作数就压入栈，并回到①，否则执行③
   ③ 若扫描到运算符，则弹出两个栈顶元素，执行相应运算，运算结果压回栈顶，回到①
3. 注意：先出栈的是“右操作数”，如果表达式合法，则最后栈中只会留下一个元素为最终结果

二、中缀表达式转前缀表达式

（一）改写方法

1. 手算
   ① 确定中缀表达式各个运算符的运算顺序
   ② 选择下一个运算符，按照**[运算符 左操作数 右操作数]**的方式组合成一个新的操作数
   ③ 如果还有运算符没有处理，就继续②
2. 选择“右优先原则”：
   A+B*(C-D)-E/F 前缀： +A-*B-CD/EF

栈和队列的应用C++实验 （含代码 截图）

application/msword 4星 超过85%的资源 81KB

下载

（二）计算方法

1. 机算
   ① 从右往左扫描下一个元素，直到处理完所有元素
   ② 若扫描到操作数就压入栈，并回到①，否则执行③
   ③ 若扫描到运算符，则弹出两个栈顶元素，执行相应运算，运算结果压回栈顶，回到①
2. 注意：先出栈的是“左操作数”，如果表达式合法，则最后栈中只会留下一个元素为最终结果

三、中缀表达式的计算

1. 就是一种中缀转后缀+后缀表达式求值的结合
2. 用栈实现中缀表达式的计算:
   ①初始化两个栈，操作数栈和运算符栈
   ②若扫描到操作数，压入操作数栈
   ③若扫描到运算符或界限符，则按照“中缀转后缀”相同的逻辑压入运算符栈(期间也会弹出运算符，中缀转后缀+ 每当弹出一个运算符时，就需要再弹出两个操作数栈的栈顶元素并执行相应运算，后缀表达式求值两个算法的结合运算结果再压回操作数栈)

第三节 栈在递归中的应用

1. 函数调用的特点:最后被调用的函数最先执行结束(LIFO)
2. 函数调用时，需要用一个栈存储: （1） 调用返回地址（2）实参
   （3） 局部变量
3. 适合于递归算法解决的问题是：可以把原始问题转换为属性相同，但是规模较小的问题，例如求n！以及求斐波那契数列

一、求正整数的阶乘

1. 代码

/*计算任意输入的整数的阶乘
#include
using namespace std;
int main()
{
    int n;
    cin>>n;
    fac_fun(n);
    return 0;
}
int fac_fun(int m)
{
    if(m==0||m==0)
         return 1;
    else
        return m*fac_fun(m-1);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

2. 注意：
   ①递归调用时，函数调用栈可称为“递归工作栈”
   ②每进入一层递归，就将递归调用所需信息压入栈顶
   每退出一层递归，就从栈顶弹出相应信息
   ③缺点:太多层递归可 能会导致栈溢出函数调用栈

二、求斐波那契数列

数据结构的渡口调度管理

application/x-rar 0星 超过10%的资源 48KB

下载

1. 代码

int FeiBo(int f)
{   if (f==0)
		return 0;
	else if (f == 1)
		return 1;
	else
		return FeiBo(f - 2) + FeiBo(f - 1);
}
int main()
{   int key = 0;
	scanf("%d", &key);
	num = FeiBo(key);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

2. 缺点：① 可能包含很多重复计算
   ② 效率太低，太多层递归可能会导致栈溢出
   ③ 可以自定义栈将递归运算改为非递归运算

总结：

1. 递归必须满足两个条件：① 递归表达式（递归体） ② 边界条件（递归出口）
2. 递归次数过多容易溢出
3. 递归效率低是因为递归调用过程中包含很多重复计算

第四节 队列在层次遍历的应用

1. 在信息处理中有一大类问题需要逐层或者逐行处理。这类问题的解决方法往往是在处理当前层或者当前行时就对下一层或下一行做预处理，把处理顺序安排好，待当前层或者当前行处理完毕，就可以处理下一层或下一行。使用队列是为了保存下一步的处理顺序。下面用二叉树层次遍历的例子，说明队列的应用。
   
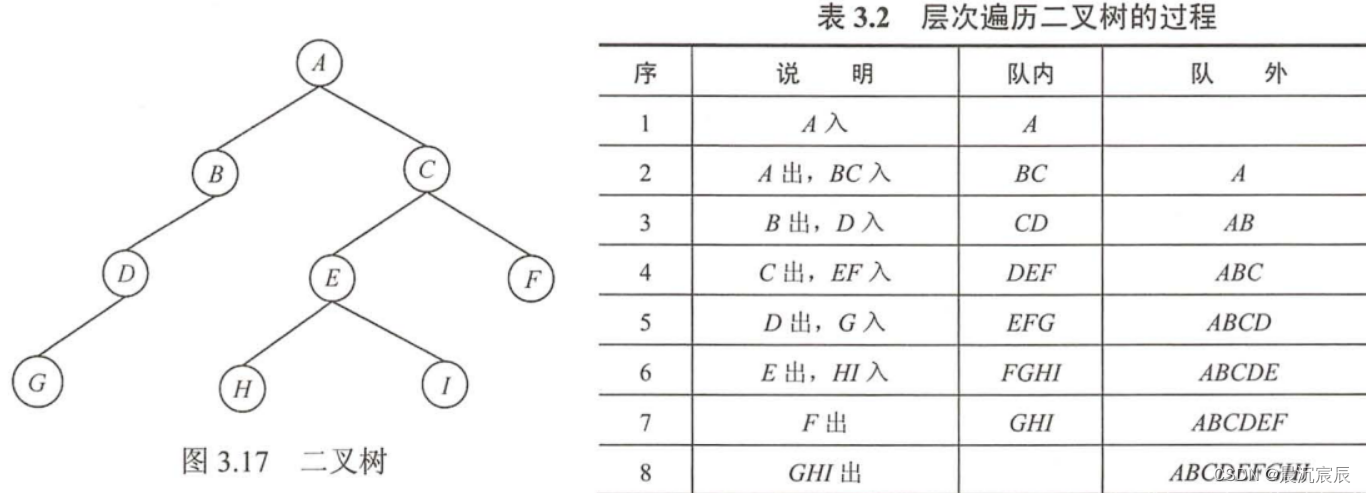
2. 层次遍历二叉树的过程
   1）根节点入队。
   2）若队空（所有结点都已经处理完毕），则结束遍历；否则重复第3步操作。
   3）队列中第一个结点出队，并访问之，若有左孩子，则左孩子入队，若有右孩子，则右孩子入队，返回第2步。

第五节 队列在计算机系统中的应用

列在计算机系统中的应用非常广泛，以下仅从两个方面来简述队列在计算机系统中的作用：第一个方面是解决主机和外部设备之间速度不匹配问题；第二个方面是解决CPU竞争问题。

① 以主机和打印机之间速度不匹配为例来说明。主机输出数据的速度远远大于打印机的打印速度，所以需要建立一个打印数据缓冲区，主机将数据缓冲区写满了可以去做其他的事情，而这个数据缓冲区就是一个队列。

② CPU资源的竞争就是一个典型的例子。像进程切换、线程切换的本质原因就是为了提高CPU的有效利用率。比如有A,B,C三个任务，但是每个任务中间都有IO请求，这样三个进程（或线程）排成一个队列（当然了实际的处理机调度是很复杂的，但是我们这儿可以简化为A先执行，遇到IO换B，依次循环执行，直到所有任务结束），这个过程中，我们看到需要处理机的任务也是一个队列的概念。还有实时交互系统，就是所有任务也是可以简化看作在一个队列中，比如按照时间片去执行这个队列，在用户端呈现出一种实时的多人操作的感官