• 【数据结构】—— 并查集

    并查集 

    ①合并两个集合

    ②查询某个元素的祖宗节点

    查找 

    通俗地讲一个故事：几个家族进行宴会，但是家族普遍长寿，所以人数众多。由于长时间的分离以及年龄的增长，这些人逐渐忘掉了自己的亲人，只记得自己的爸爸是谁了，而最长者（称为「祖先」）的父亲已经去世，他只知道自己是祖先。为了确定自己是哪个家族，他们想出了一个办法，只要问自己的爸爸是不是祖先，一层一层的向上问，直到问到祖先。如果要判断两人是否在同一家族，只要看两人的祖先是不是同一人就可以了。

    在这样的思想下，并查集的查找算法诞生了。

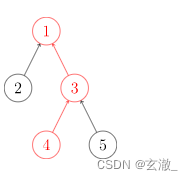
    路径压缩 

    这样的确可以达成目的，但是显然效率实在太低。为什么呢？因为我们使用了太多没用的信息，我的祖先是谁与我父亲是谁没什么关系，这样一层一层找太浪费时间，不如我直接当祖先的儿子，问一次就可以出结果了。甚至祖先是谁都无所谓，只要这个人可以代表我们家族就能得到想要的效果。把在路径上的每个节点都直接连接到根上，这就是路径压缩。

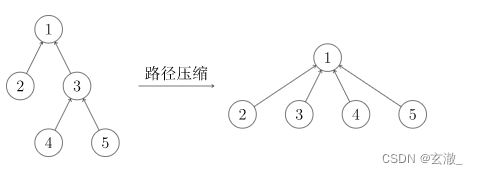
    合并 

    宴会上，一个家族的祖先突然对另一个家族说：我们两个家族交情这么好，不如合成一家好了。另一个家族也欣然接受了。
    我们之前说过，并不在意祖先究竟是谁，所以只要其中一个祖先变成另一个祖先的儿子就可以了。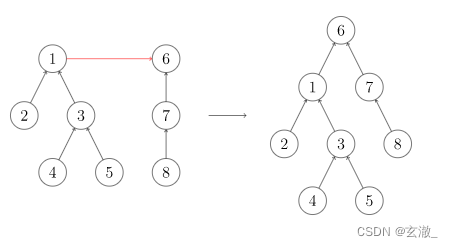

     

    ① 记录每个集合的大小 -》 绑定到根节点

    ② 记录每个点到根节点的距离 -》 绑定到每个点身上 

    AcWing 1250. 格子游戏 

    输入样例：

    1. 3 5
    2. 1 1 D
    3. 1 1 R
    4. 1 2 D
    5. 2 1 R
    6. 2 2 D

    输出样例：

    4

    问题等价于：在一次次连边的过程中，什么时候第一次连成一个环 

    可以将其看成是图论中的点跟边，出现环的时候，等价于，两个点在连通之前就已经在同一个连通块当中

    1. #include 
    2. #include 
    3. #include 
    4.  
    5. using namespace std;
    6.  
    7. const int N = 400010;
    8.  
    9. int n, m;
    10. int p[N];
    11.  
    12. // 坐标映射
    13. int get(int x, int y)
    14. {
    15.     return x * n + y;
    16. }
    17.  
    18. int find(int x)
    19. {
    20.     if(p[x] != x) p[x] = find(p[x]);
    21.     return p[x];
    22. }
    23.  
    24. int main()
    25. {
    26.     cin >> n >> m;
    27.     
    28.     for(int i = 1; i <= n * n; i ++ ) p[i] = i;
    29.     
    30.     int res = 0;
    31.     for(int i = 1; i <= m; i ++ )
    32.     {
    33.         int x, y;
    34.         char d;
    35.         cin >> x >> y >> d;
    36.         x --, y -- ;
    37.         int a = get(x, y);
    38.         int b;
    39.         if(d == 'D') b = get(x + 1, y);
    40.         else b = get(x, y + 1);
    41.         
    42.         int pa = find(a), pb = find(b);
    43.         if(pa == pb)
    44.         {
    45.             res = i;
    46.             break;
    47.         }
    48.         p[pa] = pb;
    49.     }
    50.     
    51.     if(!res) puts("draw");
    52.     else cout << res << endl;
    53.     
    54.     return 0;
    55. }
    56.

    AcWing 1252. 搭配购买 

    输入样例：

    1. 5 3 10
    2. 3 10
    3. 3 10
    4. 3 10
    5. 5 100
    6. 10 1
    7. 1 3
    8. 3 2
    9. 4 2

    输出样例：

    1

     把每一个联通块看做是一个物品，然后就变成了一个01 背包问题了。

    1. #include 
    2. #include 
    3. #include 
    4.  
    5. using namespace std;
    6.  
    7. const int N = 10010;
    8.  
    9. int n, m, vol;
    10. int v[N], w[N];
    11. int p[N];
    12. int f[N];
    13.  
    14. int find(int x)
    15. {
    16.     if(p[x] != x) p[x] = find(p[x]);
    17.     return p[x];
    18. }
    19.  
    20. int main()
    21. {
    22.     cin >> n >> m >> vol;
    23.     
    24.     for(int i = 1; i <= n; i ++ ) p[i] = i;
    25.     
    26.     for(int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
    27.     
    28.     while(m -- )
    29.     {
    30.         int a, b;
    31.         cin >> a >> b;
    32.         int pa = find(a), pb = find(b);
    33.         if(pa != pb)
    34.         {
    35.             v[pb] += v[pa];
    36.             w[pb] += w[pa];
    37.             p[pa] = p[pb];
    38.         }
    39.     }
    40.     
    41.     // 01背包问题
    42.     for(int i = 1; i <= n; i ++ )
    43.         if(p[i] == i)
    44.             for(int j = vol; j >= v[i]; j -- )
    45.                 f[j] = max(f[j], f[j - v[i]] + w[i]);
    46.     
    47.     cout << f[vol] << endl;
    48.     
    49.     return 0;
    50. }

    AcWing 237. 程序自动分析 

    输入样例：

    1. 2
    2. 2
    3. 1 2 1
    4. 1 2 0
    5. 2
    6. 1 2 1
    7. 2 1 1

    输出样例：

    1. NO
    2. YES

    思路
    1.读入数据并加入离散化数组
    2.离散化后去重，并用此数组的个数初始化并查集
    3.按照先相等后不等的顺序，先维护所有的相等关系；最后在依次查看每一对不等关系是否出现矛盾

    坑点
    1.一开始的数组大小要开两倍
    2.离散化之后注意映射是从0开始还是从1开始
    3.并查集初始化有一个小技巧，初始化的数量直接是alls数组离散化去重之后的元素个数（下标从1开始映射）
    4.离散化的查询和合并操作都应该在映射的数上进行操作

     

    1. #include 
    2. #include 
    3. #include 
    4. #include 
    5. #include 
    6.  
    7. using namespace std;
    8.  
    9. const int N = 2000010;
    10.  
    11. int n, m;
    12. int p[N];
    13. unordered_map<int, int> S;
    14.  
    15. struct Query
    16. {
    17.     int x, y, e;  
    18. }query[N];
    19.  
    20. int get(int x)
    21. {
    22.     if(S.count(x) == 0) S[x] = ++ n;
    23.     return S[x];
    24. }
    25.  
    26. int find(int x)
    27. {
    28.     if(p[x] != x) p[x] = find(p[x]);
    29.     return p[x];
    30. }
    31.  
    32. int main()
    33. {
    34.     int T; cin >> T;
    35.     
    36.     while(T -- )
    37.     {
    38.         n = 0;
    39.         cin >> m;
    40.         S.clear();
    41.         for(int i = 0; i < m; i ++ )
    42.         {
    43.             int x, y, e;
    44.             scanf("%d%d%d", &x, &y, &e);
    45.             query[i] = {get(x), get(y), e};
    46.         }
    47.         
    48.         for(int i = 1; i <= n; i ++ ) p[i] = i;
    49.         
    50.         // 合并所有的相等条件
    51.         for(int i = 0; i < m; i ++ )
    52.             if(query[i].e == 1)
    53.             {
    54.                 int pa = find(query[i].x), pb = find(query[i].y);
    55.                 p[pa] = p[pb];
    56.             }
    57.             
    58.         // 检查所有不等条件
    59.         bool has_conflict = false;
    60.         for(int i = 0; i < m; i ++ )
    61.             if(query[i].e == 0)
    62.             {
    63.                 int pa = find(query[i].x), pb = find(query[i].y);
    64.                 if(pa == pb)
    65.                 {
    66.                     has_conflict = true;
    67.                     break;
    68.                 }
    69.             }
    70.         if(has_conflict) puts("NO");
    71.         else puts("YES");
    72.     }
    73.     return 0;
    74. }

    AcWing 238. 银河英雄传说 

    输入样例：

    1. 4
    2. M 2 3
    3. C 1 2
    4. M 2 4
    5. C 4 2

    输出样例：

    1. -1
    2. 1

    ① 不问间隔多少战舰 -》 并查集

    ② 同时维护间隔多少战舰 -》 统一维护当前战舰到排头的距离

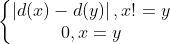
    ③ \left\{\begin{matrix}\left | d(x)-d(y) \right |,x !=y \\ 0,x=y \end{matrix}\right. 

    d[x] 表示 x 到 p[x] 的距离

    1. #include 
    2. #include 
    3. #include 
    4. #include 
    5.  
    6. using namespace std;
    7.  
    8. const int N = 30010;
    9.  
    10. int m;
    11. int p[N], sizes[N], d[N];
    12.  
    13. int find(int x)
    14. {
    15.     if(p[x] != x) 
    16.     {
    17.         int root = find(p[x]);
    18.         d[x] += d[p[x]];
    19.         p[x] = root;
    20.     }
    21.     return p[x];
    22. }
    23.  
    24. int main()
    25. {
    26.     cin >> m;
    27.  
    28.     for(int i = 1; i < N; i ++ )
    29.     {
    30.         p[i] = i;
    31.         sizes[i] = 1;
    32.     }
    33.  
    34.     while(m -- )
    35.     {
    36.         char op[2];
    37.         int a, b;
    38.         scanf("%s%d%d", op, &a, &b);
    39.         if(op[0] == 'M')
    40.         {
    41.             int pa = find(a), pb = find(b);
    42.             if (pa != pb) { // 新加的，不在一个集合中才合并！！！
    43.                 d[pa] = sizes[pb]; // pa 到 pb 的距离为 pb 中节点的个数
    44.                 sizes[pb] += sizes[pa]; // 更新 pb 中节点的个数
    45.                 p[pa] = pb; // 将 pa 合并到 pb 中
    46.             }
    47.         }
    48.         else
    49.         {
    50.             int pa = find(a), pb = find(b);
    51.             if(pa != pb) puts("-1");
    52.             else printf("%d\n", max(0, abs(d[a] - d[b]) - 1));
    53.         }
    54.     }
    55.     return 0;
    56. }

    AcWing 239. 奇偶游戏 

    输入样例：

    1. 10
    2. 5
    3. 1 2 even
    4. 3 4 odd
    5. 5 6 even
    6. 1 6 even
    7. 7 10 odd

    输出样例：

    3
    来源：《算法竞赛进阶指南》, POJ1733 , kuangbin专题
    1. #include 
    2. #include 
    3. #include 
    4. #include 
    5.  
    6. using namespace std;
    7.  
    8. const int N = 20010;
    9.  
    10. int n, m;
    11. int p[N], d[N];
    12. unordered_map<int, int> S;
    13.  
    14. int get(int x)
    15. {
    16.     if (S.count(x) == 0) S[x] = ++ n;
    17.     return S[x];
    18. }
    19.  
    20. int find(int x)
    21. {
    22.     if (p[x] != x)
    23.     {
    24.         int root = find(p[x]);
    25.         d[x] += d[p[x]];
    26.         p[x] = root;
    27.     }
    28.     return p[x];
    29. }
    30.  
    31. int main()
    32. {
    33.     cin >> n >> m;
    34.     n = 0;
    35.  
    36.     for (int i = 0; i < N; i ++ ) p[i] = i;
    37.  
    38.     int res = m;
    39.     for (int i = 1; i <= m; i ++ )
    40.     {
    41.         int a, b;
    42.         string type;
    43.         cin >> a >> b >> type;
    44.         a = get(a - 1), b = get(b);
    45.  
    46.         int t = 0;
    47.         if (type == "odd") t = 1;
    48.  
    49.         int pa = find(a), pb = find(b);
    50.         if (pa == pb)
    51.         {
    52.             if (((d[a] + d[b]) % 2 + 2) % 2 != t)
    53.             {
    54.                 res = i - 1;
    55.                 break;
    56.             }
    57.         }
    58.         else
    59.         {
    60.             p[pa] = pb;
    61.             d[pa] = d[a] ^ d[b] ^ t;
    62.         }
    63.     }
    64.  
    65.     cout << res << endl;
    66.  
    67.     return 0;
    68. }

     

     

     

     

     

     

  • 相关阅读:
    场景应用：接口和抽象类有什么区别？你平时怎么用？
    基于TI Sitara系列AM5728工业开发板——FPGA视频开发案例分享
    10【DCL数据库控制语言】
    tictoc例子理解 16-18
    vxe-table 打包部署上线，校验样式失效
    A01、分布式文件系统
    【飞桨PaddleSpeech语音技术课程】— 声纹检索系统与实践
    腾讯算法实习面试总结
    vue3+vite配置eslint&prettier
    NFT交易系统平台开发 数字藏品平台开发解决方案：区块链+艺术品搭建 打造元宇宙市场数字化经济
  • 原文地址：https://blog.csdn.net/forever_bryant/article/details/126097535