0、简介

        文章《改进的麻雀搜索优化算法及其应用》针对麻雀搜索算法(SSA)在求解目标函数最优解时，种群多样性不丰富，易陷于局部最优和多维函数求解精度差等问题，提出改进的麻雀搜索算法(ISSA)。首先，利用反向学习策略初始化种群，增加种群多样性；然后，对步长因子进行动态调整，提高算法的求解精度；最后，对侦查预警的麻雀位置更新公式引入 Levy 飞行,提高算法寻优能力和跳出局部极值的能力。

        本文复现了该论文所提的改进麻雀搜索算法(ISSA)，并将其与常规GA、PSO、SSA算法进行对比。

1、ISSA原理

       具体 请参考文献《改进的麻雀搜索优化算法及其应用》。

       原始SSA更新方式如下：

 

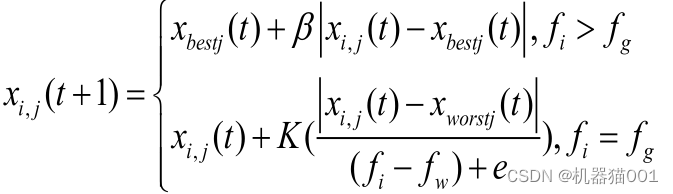
        Xbestj (t)表示当前全局最佳位置，β 为服从均值为 0，方差为 1 的正态分布随机数的步长控制参数，K∈[-1,1]表示麻雀运动方向，也是步长控制参数，fi表示当前麻雀的适应度值，fg 和fw 表示当前全局最优值和最差值，e 为一个常数，是为了避免分母为 0。可以看出步长控制参数 β 和 K在平衡全局搜索能力与局部开发能力方面发挥重要作用。 

        该文章对SSA的改动如下：（所有公式直接来源于该文章！）

1.1 反向学习策略（改善随机生成初始化种群分布不均、种群多样性减少问题）

       SSA 采用的是随机生成初始种群，生成的种群分布不均匀，会导致种群多样性减少，种群质量不高，影响算法的收敛速度，因此改进的麻雀搜索算法(ISSA)采用反向学习策略来解决这一问题。利用反向学习策略生成种群的主要思想：首先随机生成初始种群，然后根据初始种群生成其反向种群，从中选择较优的种群作为下一代种群。反向学习策略会选择更靠近的个体作为种群的最初个体，这样每个个体都离最优解更近一步，以便提高种群的所有个体收敛速度。并且反向学习策略还可以通过搜索更多有效区域来提高群体的多样性，增强算法的全局搜索能力。

1.2 步长因子动态调整(减少出现局部最优的概率)

        在 SSA 算法中，图1中的步长控制参数 β 和 K在平衡全局搜索能力与局部开发能力方面发挥重要作用，但因为 β 和 K 都为随机数，无法满足算法在解空间的探索，可能导致 SSA 陷入局部最优，于是对步长控制参数 β 和 K 进行优化，较大的控制参数便于全局搜索，较小的控制参数促进局部开发。

        对步长控制参数 β 和 K 的改进如下所示：

 

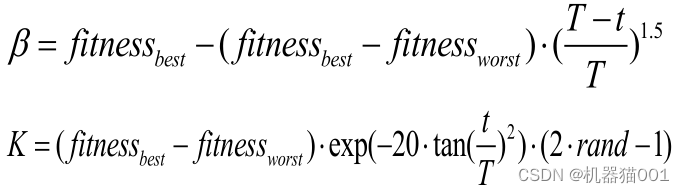
1.3  Levy 飞行（提高算法寻优能力和跳出局部极值的能力）

        将Levy 飞行策略引入式(3)中的麻雀最优位置，因为SSA 会根据当前位置与麻雀最优位置的距离来进行位置更新，改进后的 SSA 大大降低了麻雀陷入局部最优的风险，而且仍然能充分执行局部探索，改进公式如下所示：

 

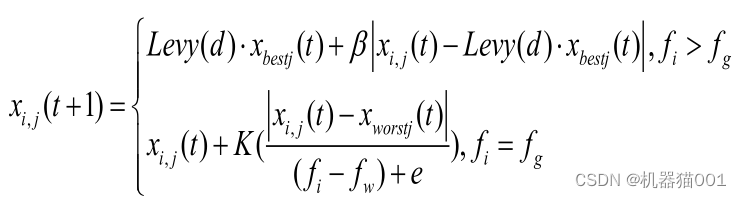
其中，d 为向量维度，Levy 计算公式如下所示：

 

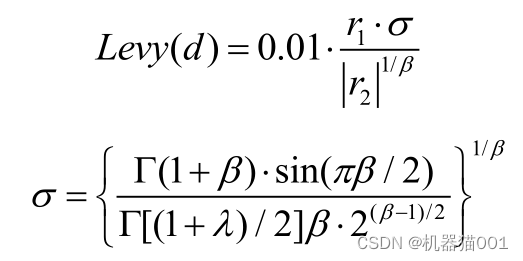
其中，Г 为伽马函数，β 为常数，r 1 和 r 2 为 0 到 1的随机数。

2、ISSA效果分析

在标准测试函数F1上的结果：

        

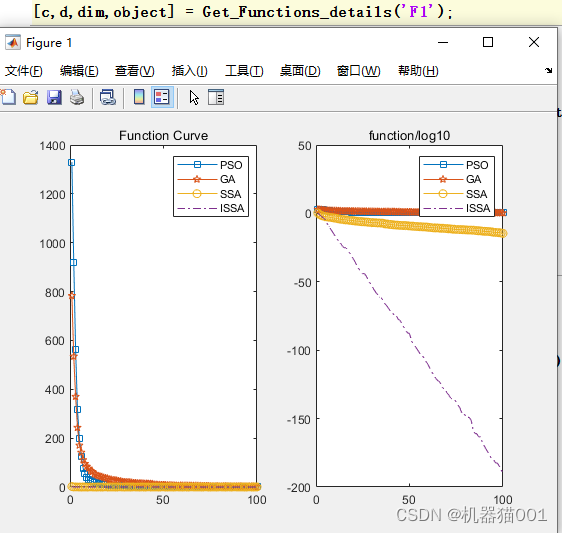
在标准测试函数F3上的寻优结果：

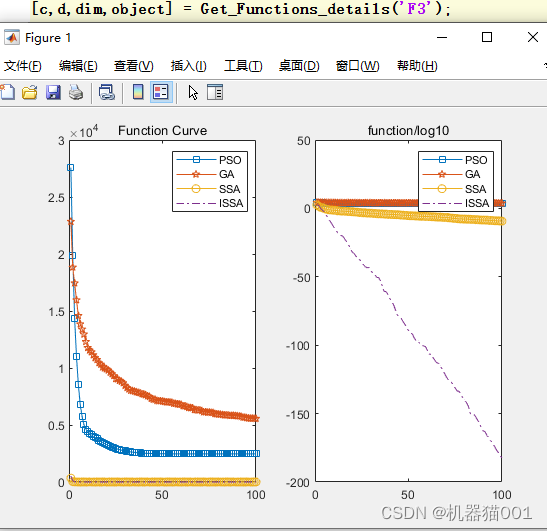
在标准测试函数F5上的寻优结果：

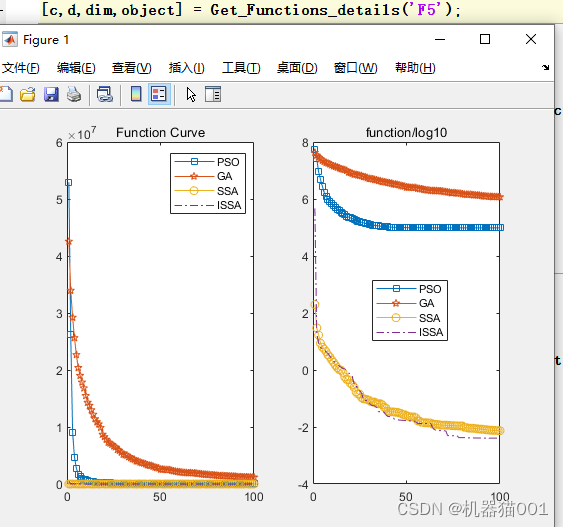
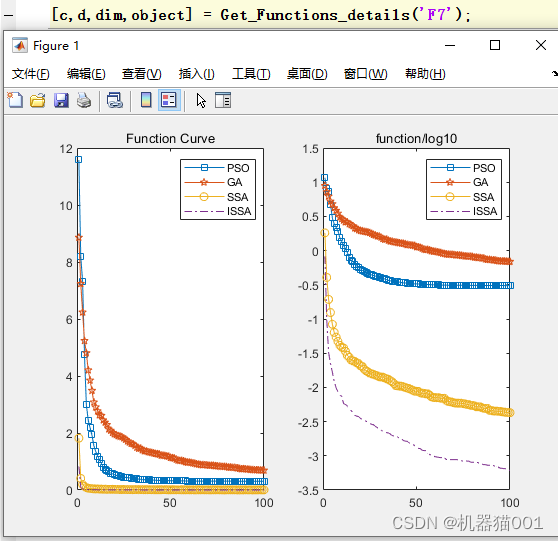
在标准测试函数F7上的寻优结果：

 

3、结论

        2中分析结果验证了改进后的ISSA算法具有更强的全局寻优能力，不易陷入局部最优。