---

题目1——滑动窗口的最大值

给定一个长度为n的数组nums和滑动窗口的大小size，找出滑动窗口里数值的最大值。
例如输入数组{2,3,4,2,6,2,5,1}及滑动窗口的大小3，那么一共存在6个滑动窗口，他们的最大值分别为{4,4,6,6,6,5}。
要求：空间复杂度O(n)，时间复杂度O(n)。

示例
输入：[2,3,4,2,6,2,5,1],3
输出：[4,4,6,6,6,5]

解题思路

暴力解决，直接遍历所有窗口，求出每个窗口的最大值。
但是时间复杂度较高O(nm)，n为数组长度，m为窗口长度，空间复杂度O(1)，返回结果不算入空间开销。

如果一个新的数字进入窗口，若它比窗口内其它数字都要大，那么这个数字之前的数字都不会选择，因为它们会比这个数字早离开窗口，在这期间的滑动窗口内，我们选择的都是这个最大的数字。
从这里分析可知，每次进入大数字时，应该排除掉之前的小值，并且每次窗口滑动时，需要弹出窗口最前面的值，所以可以选择双端队列来实现。

Java中双端队列的实现是ArrayDeque，它允许我们从两端进行存取操作，既可以作为栈，又可以作为队列使用。ArrayDeque类的方法如下：

• 头部插入元素：offerFirst(e)，返回状态值；addFirst(e)，失败会抛出异常；
• 头部移除元素：pollFirst()，删除并返回元素；removeFirst()，删除并返回元素，失败会抛出异常；
• 获取头部元素：peekFirst()，获取第一个元素；getFirst()，获取第一个元素，失败会抛出异常；
• 尾部插入元素： offerLast(e)，返回状态值；addLast(e)，失败会抛出异常；
• 尾部移除元素：pollLast()，删除并返回元素；removeLast()，删除并返回元素，失败会抛出异常；
• 获取尾部元素：peekLast()，获取最后一个元素；getLast()，获取最后一个元素，失败会抛出异常。

代码实现

//暴力解决
import java.util.*;
public class Solution {
    public ArrayList<Integer> maxInWindows(int [] num, int size) {
        ArrayList<Integer> res = new ArrayList<Integer>();
        if(num.length < size){
            return res;
        }
        //窗口数量为num.lenght-size+1
        for(int i=0;i<num.length-size+1;i++){
            int max = 0;
            for(int j=i;j<i+size;j++){
                if(num[j]>max)
                    max = num[j];
            }
            res.add(max);
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

//双端队列，时间复杂度O(n)，空间复杂度为O(m)，m为窗口的长度
import java.util.*;
public class Solution {
    public ArrayList<Integer> maxInWindows(int [] num, int size) {
        ArrayList<Integer> res = new ArrayList<Integer>();
        if(num.length < size){
            return res;
        }
        ArrayDeque<Integer> dq = new ArrayDeque<Integer>();
        //先遍历一个窗口，
        for(int i=0;i<size;i++){
            //去掉前面的小于自己的值
            while(!dq.isEmpty() && num[dq.peekLast()]<num[i])
                dq.pollLast();
            dq.add(i);
        }
        //遍历后续的数组
        for(int i=size;i<num.length;i++){
            res.add(num[dq.peekFirst()]);
            //滑动窗口，移除队首的值
            while(!dq.isEmpty() && dq.peekFirst()<(i-size+1))
                dq.pollFirst();
            //加入新的值前，去除掉比自己先进队列并小于自己的值
            while(!dq.isEmpty() && num[dq.peekLast()]<num[i])
                dq.pollLast();
            dq.add(i);
        }
        res.add(num[dq.pollFirst()]);
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

题目2——矩阵最长递增路径

给定一个n行m列矩阵matrix，矩阵内所有数均为非负整数，你需要在矩阵中找到一条最长路径，使这条路径上的元素是递增的，并输出这条最长路径的长度。
这个路径必须满足以下条件：

1. 对于每个单元格，你可以往上，下，左，右四个方向移动，不能在对角线方向上移动或移动到边界外。
2. 不能走重复的单元格，即每个格子最多只能走一次。
   要求：空间复杂度O(nm)，时间复杂度O(nm)。

示例
输入：[[1,2,3],[4,5,6],[7,8,9]]
输出：5(最长路径1->2->3->6->9)

解题思路

使用深度优先搜索，从初始点开始，沿着同一个分支遍历，直到该分支结束，然后回溯到上一级继续沿着一个分支走到底，如此往复，直到所有结点都被访问到。
为了找到最长的递增路径，矩阵中的每个元素很有可能都是这个路径的起点，所以我们遍历整个矩阵中的元素，将每个元素作为起始点，然后进行深度优先搜索，寻找最长递增路径。具体做法如下：

• 使用一个数据b来记录每个起始点的最大递增路径，在递归过程中如果访问到了就不需要重复访问；
• 对于每个起始点，使用dfs查找最长的递增路径，dfs中，只要下一个位置比当前位置数字大，就可以深入。

代码实现

import java.util.*;
public class Solution {
    public int dfs(int[][] matrix,int[][] b,int i,int j){
        int n = matrix.length;
        int m = matrix[0].length;
        if(b[i][j] != 0)
            return b[i][j];
        b[i][j]++;
        if(i-1>=0 && matrix[i-1][j]>matrix[i][j]){
            b[i][j] = Math.max(b[i][j],dfs(matrix,b,i-1,j)+1);
        }
        if(i+1<n && matrix[i+1][j]>matrix[i][j]){
            b[i][j] = Math.max(b[i][j],dfs(matrix,b,i+1,j)+1);
        }
        if(j-1>=0 && matrix[i][j-1]>matrix[i][j]){
            b[i][j] = Math.max(b[i][j],dfs(matrix,b,i,j-1)+1);
        }
        if(j+1<m && matrix[i][j+1]>matrix[i][j]){
            b[i][j] = Math.max(b[i][j],dfs(matrix,b,i,j+1)+1);
        }
        return b[i][j];
    }
    public int solve (int[][] matrix) {
        int n = matrix.length;
        int m = matrix[0].length;
        int[][] b = new int[n][m];
        int res = 0 ;
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                res = Math.max(res,dfs(matrix,b,i,j));
            }
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

题目3——顺时针旋转矩阵

有一个n*n整数矩阵，请编写一个算法，将矩阵顺时针旋转90度，返回旋转后的矩阵。
要求：空间复杂度 O(n^2)，时间复杂度 O(n^2)。
进阶：空间复杂度 O(1)，时间复杂度 O(n^2)。

示例
输入：[[1,2,3],[4,5,6],[7,8,9]],3
输出：[[7,4,1],[8,5,2],[9,6,3]]

解题思路

使用一个辅助数组来存储新的矩阵，可以发现，原矩阵元素mat[i][j]旋转后该值在新矩阵的res[j][n-i-1]的位置，但是这样时间复杂度O(n^2)，空间复杂度O(n ^2)。
可以发现顺时针旋转后的矩阵，就是矩阵转置，然后每行再翻转，这样只需要一个辅助变量即可实现旋转。

代码实现

import java.util.*;
public class Solution {
    public int[][] rotateMatrix(int[][] mat, int n) {
        int temp;
        for(int i=0;i<n;i++){
            for(int j=0;j<i;j++){
                temp = mat[i][j];
                mat[i][j] = mat[j][i];
                mat[j][i] = temp;
            }
        }
        for(int i=0;i<n;i++){
            for(int j=0;j<n/2;j++){
                temp = mat[i][j];
                mat[i][j] = mat[i][n-j-1];
                mat[i][n-j-1] = temp;
            }
        }
        return mat;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

题目4——接雨水问题

给定过一个整型数组arr，已知其中所有的值都是非负的，将这个数组看作一个柱子高度图，计算按此排列的柱子，下雨之后能接多少雨水(数组以外的区域高度视为0)。
要求：时间复杂度O(n)。

示例
输入：[3,1,2,5,2,4]
输出：5

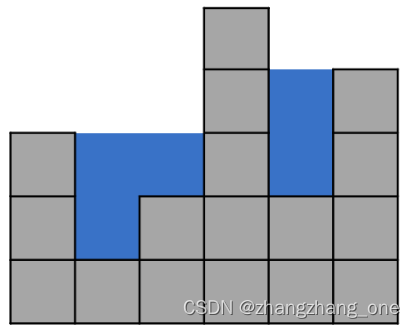
解题思路

我们可以将整个图看成一个水桶，两边是水桶的板，由较短的板控制水桶的最高水量，但是水桶中间可能会出现更高的边，这样就将一个水桶分割成了两个水桶，中间那条边就是两个水桶的边。
这样我们可以使用对撞指针往中间靠，如果遇到更低的柱子，就用较短的板减去这个底，就是这一列的接水量，如果遇到更高的柱子，就是新的边界，更新边界的大小。

代码实现

import java.util.*;
public class Solution {
    public long maxWater (int[] arr) {
        if(arr.length == 0)
            return 0;
        long res = 0;
        int left = 0;
        int right = arr.length-1;
        int maxL = 0;
        int maxR = 0;
        //对撞指针往中间靠
        while(left<right){
            //每次维护往中间走的边界
            maxL = Math.max(maxL,arr[left]);
            maxR = Math.max(maxR,arr[right]);
            if(maxR > maxL)
                //短的边界减去底，就是这一列的接水量
                res += maxL-arr[left++];
            else 
                res += maxR-arr[right--];
        }
        return res;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24