牛客2022 暑期多校4 D Jobs (Easy Version)（递推优化策略）

参考

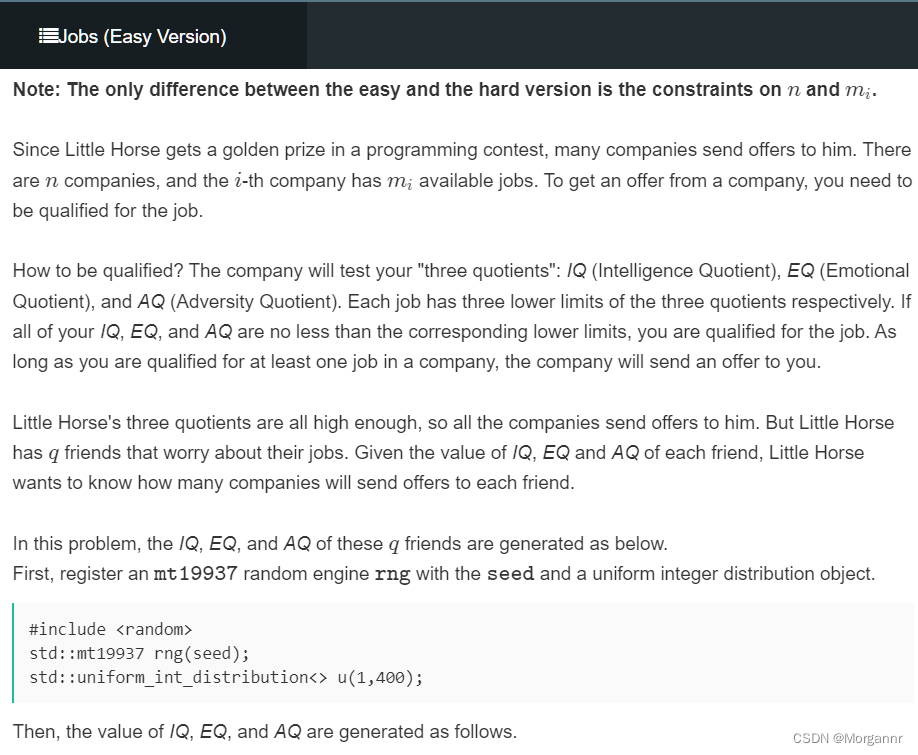
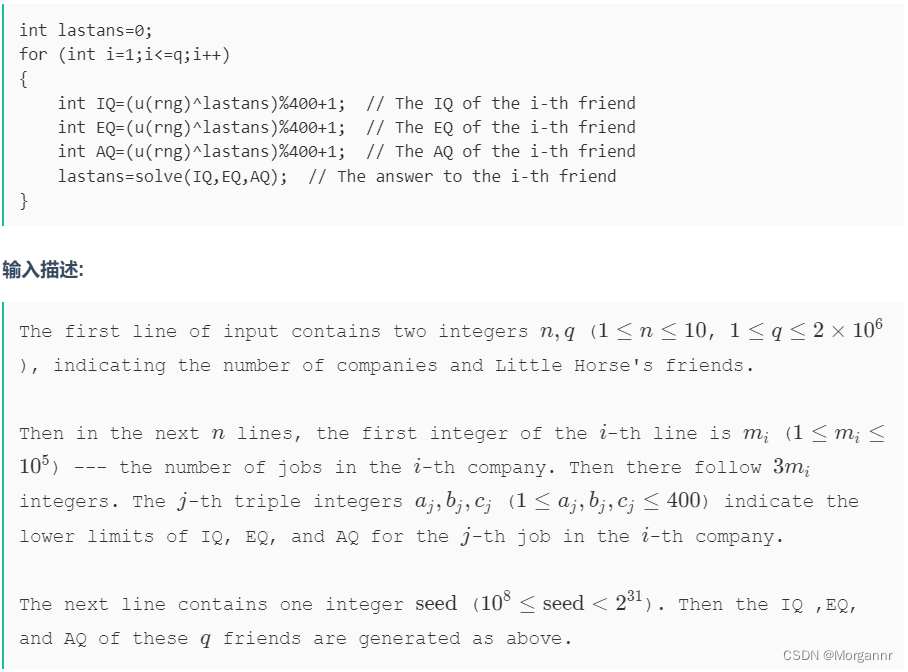
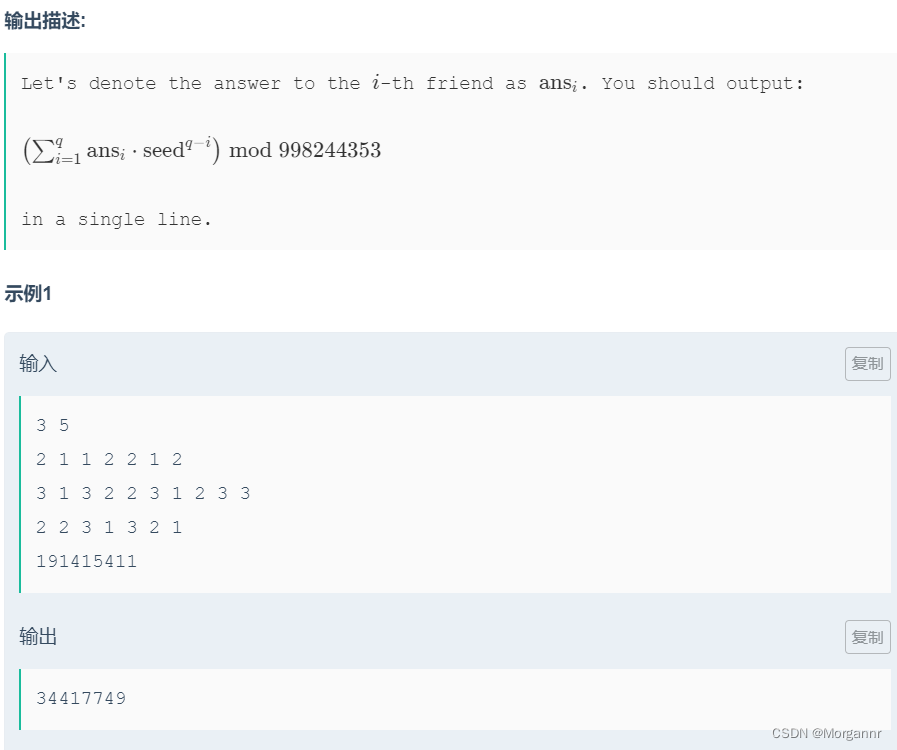
题意：

给你 n 个公司的求职岗位，每个岗位有 三个要求：EQ、IQ、AQ，当你的这三项指标都 大于等于这个职位的标准时，这个公司就会邀请你入职。现在你有 q 个朋友，你要算出他们 分别会被多少个公司邀请，再根据 公司的数量 算出：
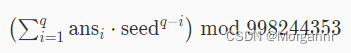其中 ans 是第 i 个朋友收到公司邀请的数目，seed 是题目给我们的随机数种子。

思路：

这一题的主要问题就是，我们怎么能够知道 对于第 i 家公司，应聘者的三商是否能完全满足某个职位的需求。

先想 暴力怎么做：直接 for 循环用应聘者的三商对比当前公司的所有职位，来看 当前公司是否能邀请我们。

但这样的 时间复杂度是：n * q * mi，显然不行。

• 提示 1：查看 数据范围 我们发现 除了 职位数 mi 和 应聘者数 q 是常见的 1e5、1e6 级别。公司数 n 和三商的上限都是很小的，我们可以试着从这里想办法。

• 提示 2：我们 并不用知道一个公司有多少职位是应聘者可以满足的，只要有 一个职位满足即可。

可以类比 二维前缀和，我们准备一个 三维数组，把 应聘公司的编号看成 i（新增的一维），把 应聘者 IQ 看成 j，EQ 看成 k，AQ 为 f[i][j][k]，

f[i][j][k] 表示：在 应聘者的 IQ 范围 1 ~ j，EQ 范围 1 ~ k 的情况下，能够通过 第 i 家公司 招聘的 AQ 的最小值。

那么对于应聘者的 三商 abc 来说，只要 f[a][b] 小于等于 c，那么这个公司就是能够邀请我们的。

预处理完 f 数组之后，后续我们就可以在 O(1) 时间复杂度 内 判断这个公司是否能邀请应聘者。

注意：

• 因为有 n 个公司，所以我们开的其实是一个 15 * 410 * 410 的 三维数组，实际做法和二维数组一样。
• 对于最终计算结果，用快速幂求出 seed 的 q - i 次幂再乘上 lastans，把 n 个朋友的运算结果加起来 即可。

#include <bits/stdc++.h>
#include <random>

using namespace std;
//#define map unordered_map
#define int long long
int seed;
uniform_int_distribution<> u(1, 400);
const int mod = 998244353;
int n, q;
const int N = 1e5 + 10, M = 410;
int f[15][M][M];
int ans;

int qmi(int a, int b)
{
    int res = 1;
    while (b)
    {
        if (b & 1) res = res * a % mod;
        b >>= 1;
        a = a * a % mod;
    }
    return res;
}

int solve(int iq, int eq, int aq) {
    int cnt = 0;
    for (int i = 1; i <= n; ++i) {
        if (aq >= f[i][iq][eq]) ++cnt;
    }
    return cnt;
}

signed main()
{
    cin >> n >> q;
    memset(f, 0x3f, sizeof f);
    for (int i = 1; i <= n; ++i) {
        int m; scanf("%lld", &m);
        for (int j = 1; j <= m; ++j) {
            int a, b, c;
            scanf("%lld%lld%lld", &a, &b, &c);
            f[i][a][b] = min(f[i][a][b], c);
        }
        for (int j = 1; j <= 400; ++j) {
            for (int k = 1; k <= 400; ++k) {
                f[i][j][k] = min(min(f[i][j][k], f[i][j][k - 1]), f[i][j - 1][k]);
            }
        }
    }
    cin >> seed;
    mt19937 rng(seed);
    int lastans = 0;
    for (int i = 1; i <= q; ++i) {
        int IQ = (u(rng) ^ lastans) % 400 + 1;  // The IQ of the i-th friend
        int EQ = (u(rng) ^ lastans) % 400 + 1;  // The EQ of the i-th friend
        int AQ = (u(rng) ^ lastans) % 400 + 1;  // The AQ of the i-th friend
        lastans = solve(IQ, EQ, AQ);  // The answer to the i-th friend
        ans = (ans + lastans * qmi(seed, q - i)) % mod;
    }
    cout << ans << '\n';

    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65