【1161. 最大层内元素和】

来源：力扣（LeetCode）

描述：

给你一个二叉树的根节点 root。设根节点位于二叉树的第 1 层，而根节点的子节点位于第 2 层，依此类推。

请返回层内元素之和 最大 的那几层（可能只有一层）的层号，并返回其中 最小 的那个。

示例 1：

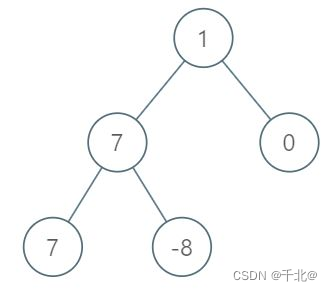
输入：root = [1,7,0,7,-8,null,null]
输出：2
解释：
第 1 层各元素之和为 1，
第 2 层各元素之和为 7 + 0 = 7，
第 3 层各元素之和为 7 + -8 = -1，
所以我们返回第 2 层的层号，它的层内元素之和最大。
1
2
3
4
5
6
7

示例 2：

输入：root = [989,null,10250,98693,-89388,null,null,null,-32127]
输出：2
1
2

提示：

• 树中的节点数在 [1, 10⁴]范围内
• -10⁵ <= Node.val <= 10⁵

方法一：深度优先搜索

我们可以采用深度优先搜索来遍历这棵二叉树，递归的同时记录当前的层号。

相比哈希表，这里我们采用效率更高的动态数组来维护每一层的元素之和，如果当前层号达到了数组的长度，则将节点元素添加到数组末尾，否则更新对应层号的元素之和。

然后遍历数组，找到元素之和最大，且层号最小的元素。

代码：

class Solution {
    vector<int> sum;

    void dfs(TreeNode *node, int level) {
        if (level == sum.size()) {
            sum.push_back(node->val);
        } else {
            sum[level] += node->val;
        }
        if (node->left) {
            dfs(node->left, level + 1);
        }
        if (node->right) {
            dfs(node->right, level + 1);
        }
    }

public:
    int maxLevelSum(TreeNode *root) {
        dfs(root, 0);
        int ans = 0;
        for (int i = 0; i < sum.size(); ++i) {
            if (sum[i] > sum[ans]) {
                ans = i;
            }
        }
        return ans + 1; // 层号从 1 开始
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

执行用时：144 ms, 在所有 C++ 提交中击败了94.63%的用户
内存消耗：102.2 MB, 在所有 C++ 提交中击败了97.01%的用户
复杂度分析
时间复杂度： O(n)，其中 n 是二叉树的节点个数。
空间复杂度： O(n)。最坏情况下二叉树是一条链，需要 O(n) 的数组空间以及 O(n) 的递归栈空间。

方法二：广度优先搜索

由于计算的是每层的元素之和，用广度优先搜索来遍历这棵树会更加自然。

对于广度优先搜索，我们可以用队列来实现。初始时，队列只包含根节点；然后不断出队，将子节点入队，直到队列为空。

如果直接套用方法一的思路，我们需要在队列中存储节点和节点的层号。另一种做法是一次遍历完一整层的节点，遍历的同时，累加该层的节点的元素之和，同时用这层的节点得到下一层的节点，这种做法不需要记录层号。

为了代码实现的方便，我们可以使用两个动态数组，第一个数组 q 为当前层的节点，第二个数组 nq 为下一层的节点。遍历 q 中节点的同时，把子节点加到 nq 中。遍历完当前层后，将 q 置为 nq。

代码：

class Solution {
public:
    int maxLevelSum(TreeNode *root) {
        int ans = 1, maxSum = root->val;
        vector<TreeNode*> q = {root};
        for (int level = 1; !q.empty(); ++level) {
            vector<TreeNode*> nq;
            int sum = 0;
            for (auto node : q) {
                sum += node->val;
                if (node->left) {
                    nq.emplace_back(node->left);
                }
                if (node->right) {
                    nq.emplace_back(node->right);
                }
            }
            if (sum > maxSum) {
                maxSum = sum;
                ans = level;
            }
            q = move(nq);
        }
        return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

执行用时：152 ms, 在所有 C++ 提交中击败了84.78%的用户
内存消耗：109 MB, 在所有 C++ 提交中击败了6.87%的用户
复杂度分析
时间复杂度： O(n)，其中 n 是二叉树的节点个数。
空间复杂度： O(n)。最坏情况下，数组中有 O(n) 个节点。
author：LeetCode-Solution