降维算法实战项目（2）—使用PCA对图像降维（Python代码+数据集）

在这部分练习中，我们将学习人脸图像上运行PCA，看看如何在实践中使用它来减少维度。

老规矩，先放出数据集：

链接：https://pan.baidu.com/s/1R0oiqoWHV2iR8sc3YHkMoA
提取码：6666

导入需要用到的包

from numpy import *
from scipy.io import loadmat
import matplotlib.pyplot as plt
1
2
3

导入数据

faces_data = loadmat('data/ex7faces.mat')
print(faces_data)
X=faces_data['X']
print(X.shape)
1
2
3
4

结果为：

{'__header__': b'MATLAB 5.0 MAT-file, Platform: PCWIN64, Created on: Mon Nov 14 23:46:35 2011', '__version__': '1.0', '__globals__': [], 'X': array([[ -37.86631387,  -45.86631387,  -53.86631387, ..., -110.86631387,
        -111.86631387,  -99.86631387],
       [   8.13368613,   -0.86631387,   -8.86631387, ...,  -34.86631387,
          -8.86631387,    0.13368613],
       [ -32.86631387,  -34.86631387,  -36.86631387, ..., -110.86631387,
        -111.86631387, -111.86631387],
       ...,
       [ -46.86631387,  -24.86631387,   -8.86631387, ...,   90.13368613,
          80.13368613,   59.13368613],
       [  19.13368613,   16.13368613,   14.13368613, ...,  -38.86631387,
         -41.86631387,  -46.86631387],
       [-108.86631387, -106.86631387, -102.86631387, ...,   17.13368613,
          17.13368613,   18.13368613]])}
1
2
3
4
5
6
7
8
9
10
11
12
13

(5000, 1024)
1

说明我们的数据集有5000个样本，每个样本有1024个特征。

可视化

我们可视化一下前100张人脸图像：

def plot_100_image(X):
    fig,ax=plt.subplots(nrows=10,ncols=10,figsize=(10,10))
    for c in range(10):
        for r in range(10):
            ax[c,r].imshow(X[10*c+r].reshape(32,32).T,cmap='Greys_r')
            ax[c,r].set_xticks([])
            ax[c,r].set_yticks([])
    plt.show()

plot_100_image(X)
1
2
3
4
5
6
7
8
9
10

结果如下图所示：

接下来我们应用PCA算法的步骤与之前在二维数据集上的步骤一致：
1.去均值化

2.计算协方差矩阵

3.计算特征值和特征向量

我们不再细致讲解，有需要的可以看我之前的博客：

https://blog.csdn.net/wzk4869/article/details/126074158?spm=1001.2014.3001.5502

直接放出对应的代码：

def reduce_mean(X):
    X_reduce_mean=X-X.mean(axis=0)
    return X_reduce_mean
X_reduce_mean=reduce_mean(X)

def sigma_matrix(X_reduce_mean):
    sigma=(X_reduce_mean.T @ X_reduce_mean)/X_reduce_mean.shape[0]
    return sigma
sigma=sigma_matrix(X_reduce_mean)

def usv(sigma):
    u,s,v=linalg.svd(sigma)
    return u,s,v
u,s,v=usv(sigma)
print(u)

def project_data(X_reduce_mean, u, k):
    u_reduced = u[:,:k]
    z=dot(X_reduce_mean, u_reduced)
    return z
z = project_data(X_reduce_mean, u, 100)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

我们接下来还原数据，这里选择只保留100个特征：

def recover_data(z, u, k):
    u_reduced = u[:,:k]
    X_recover=dot(z, u_reduced.T)
    return X_recover
X_recover=recover_data(z,u,100)
1
2
3
4
5

我们看一下最后降维后的图像：

plot_100_image(X_recover)
1

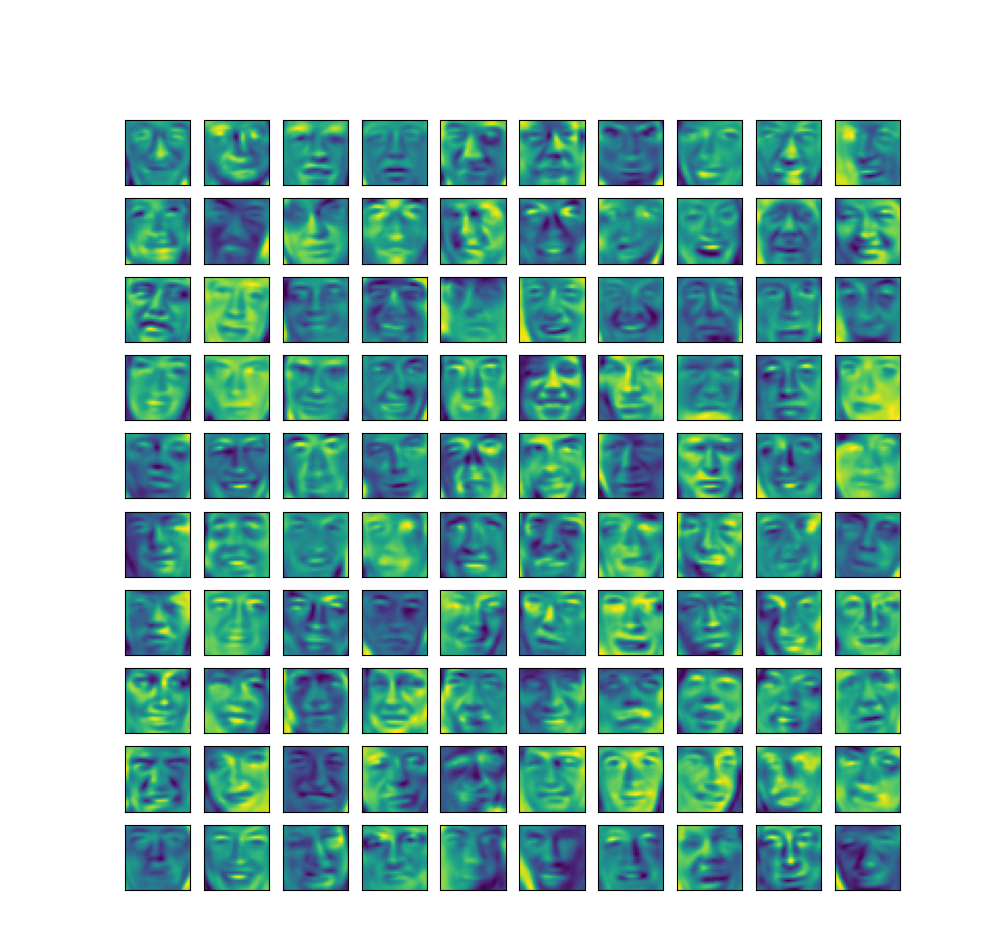
我们对比两张图片，可以很明显的看出，第二张图片保留的特征较少，已经导致脸部有些模糊。

最后唠叨一句

如果不设置 cmap='Greys_r' 会很阴间：

最开始的100张人脸：

降维后的人脸：