一.校验码

        校验码通常是一组数字的最后一位，由前面的数字通过某种运算得出，用以检验该组数字的正确性。常见的校验码有身份证的最后一位。而在计算机系统传输数据过程中，为了确保数据传送过程中正确无误，会使用校验码来进行差错和纠错，一般的数据传输会包含数据+校验位，校验码根据不同的算法得出，常见的校验码方式有三种：奇偶校验码、海明校验码以及CRC循环冗余校验码。

​

二．码距

       对比两个数据对应相同位置上数据的不同的个数称为码组的距离，简称码距。例如101011和011111这两组数据：

       其中有三个位置的数据（位置一、二和四）是不同的，所以码距为三。

三．奇偶校验码

       奇校验和偶校验合起来统称为奇偶校验，校验方法可以分为水平校验和垂直校验，校验原理是：

 （1）奇校验：数据中1的个数为奇数个。

        例子：

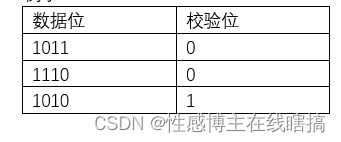
（2）偶校验：数据中1的个数为偶数个。

        例子：

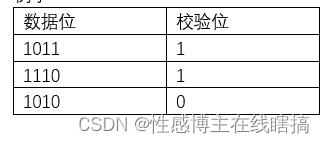
（3）水平校验：每个数据都添加校验位，使信息位与校验位处于同一行。

        例子：上面两个例子就是水平奇偶校验的例子。

（4）垂直校验：把一组数据分成若干组，垂直排序下来，再进行奇偶校验。

        例子：1010 1111 1101 1010

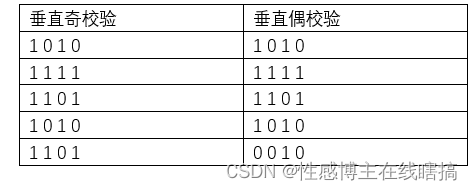
        其中校验位是最下方的：

        而每个校验位都是通过垂直对比每个数据得出的：

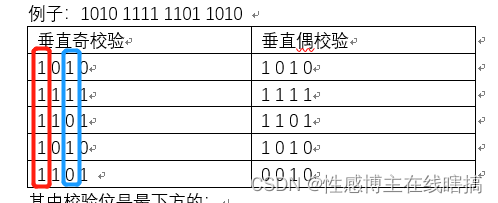
          当然，奇偶校验码的缺点很明显：

（1）单独使用奇偶校验法只能检测出奇数位/偶数位出错，不能同时检测出两种结果。而且也并不是所有数据都能检错（-..-这……）

        例子：数据0001，奇校验为00010，传输过程中发生错误变成了1001，奇校验为10011，1的个数仍旧是奇数个，并不能进行校验。

（2）使用奇偶校验法并不能知道哪一位置出了错。

四．海明验证码

       顾名思义，海明校验码是由一个名为Richard Hamming的人设计的，是一种利用奇偶性来检错和纠错的校验方法，该方法是把数据的每一个二进制位分配在几个不同的偶校验位的组合中，当某一位出错后，就会引起相关的几个校验位的值发生变化，这不但可以发现出错，还能指出是哪一位出错。

       设数据位共有n位，校验位共有k位，，那么n和k之间必须满足以下关系：

                        ​​​​​​​        ​​​​​​​        

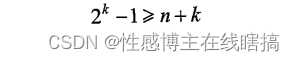
       注：其中2的k次幂代表校验码的位置（重点要考的）

       例子：我们来举个生动的例子诠释下海明校验码是怎么用的，比如计算数据 101101100 的海明校验码是多少？

       第一步：从例子我们可以得知数据位n=9位，把n代入到上面那个公式中可以算出k=4位（可以自己算算），那么就知道了校验码有4位

       第二步：计算校验码的位置，由上面公式可以知道，2的k次幂代表校验码的位置，所以2的4次方的意思就是校验位在1，2，4，8这四个位置

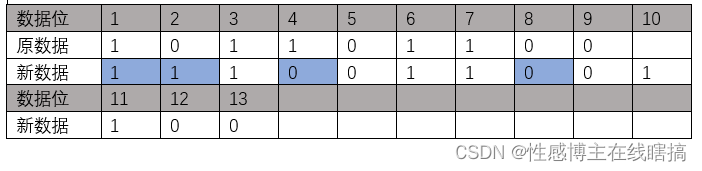
        第三步：把原来的数据重新编排，把校验位加插在其中：

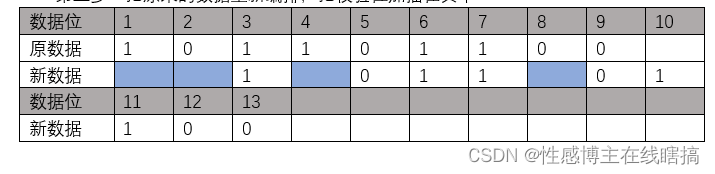
        第四步：最重要的一步，确认校验关系，看数据位的位置是哪几个校验位的位置的和：

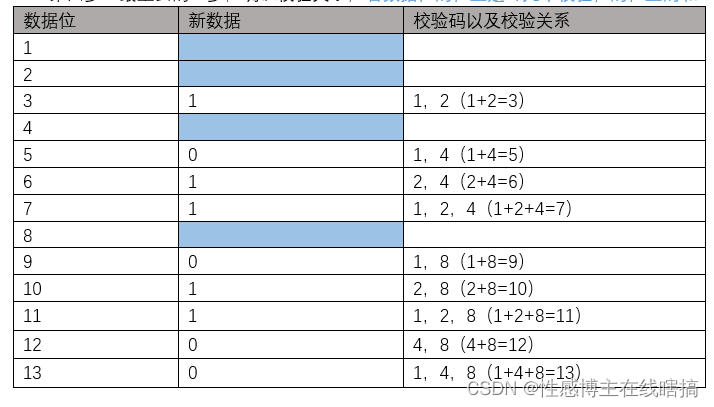
        第五步：汇总校验关系以及异或运算

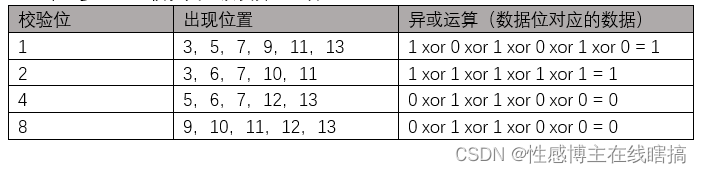
       最后一步：最后得出海明校验码为1100