---

基本概念

机器学习就是去寻找一个复杂的函数
深度学习：找一个函数，这个函数用类神经网络表示

函数的输入可以是一个向量、矩阵（images）、序列（语音）
输出可以是一个数（regression）、可以是一个类别（分类）、文本、画图等

课程任务

• Supervised Learning (监督学习)
• Self-supervised Learning (自监督学习)
• Generative Adversarial Network (生成对抗网络)
• Reinforcement Learning (强化学习)
• Anomaly Detection (异常检测)
• Explainable AI (可解释性 AI)
• Model Attack (模型攻击)
• Domain Adaptation (域自适应)
• Network Compression (让模型变小)
• Life-long Learning (终身学习)
• Meta learning (学习如何学习)

机器学习的步骤

1. Function with Unknown Parameters

$y=b+w{x}_1$
$y$：预测的值
$x$：feature
$w$：weight
$b$：bias
Model：在机器学习里面就是指带参数的函数

2. Define Loss from Training Data

Loss：是一个带参函数
输入：$b$ 和 $w$
输出：代表某一组 $b$ 和 $w$ 好还是不好
$L(b,w)$

例：求 $L(0.5k,1)$
$y=b+w{x}_1$ $==>$ $y=0.5k+1x_1$
假如带入后求得的 $y=5.3k$ 而实际的 $\hat{y}=4.9k$ (label)
$e_1=|y-\hat{y}|=0.4k$
$e_2,e_3,...e_n$都可以这样计算
Loss: $$L=\frac{1}{N}\sum _n{e}_n$$

越小代表这一组参数越好。

有多种计算方式：
MAE(mean absolute error): $e=|y-\hat{y}|$
MSE(mean square error):$e=(y-\hat{y}{)}^2$
cross-entropy

根据 $w$ 和 $b$ 画出的 $Loss$ 的等高线图叫做 Error Surface（二维）

3. Optimization

目的：找最好的 $w$ 和 $b$

Optimization的方法：Gradient Descent

先给出 $Loss$ 与 $w$ 的变化图 (Error Surface 一维)

步骤:

1. Pick an initial value $W^0$
2. 对此时的 $w$ 求导(算微分)：计算切线斜率
3. 更新 $w$
4. 反复上面的操作

可能出现局部最优解(Local minima)

切线斜率负的：切线左高右低，所以如果应该向右边前进（w = w - 学习率 * 斜率）

决定步长的因素有两个：

1. 斜率（斜率越大步长越大）
2. 学习率（自己设置的一个参数）

hyperparameters：需要自己设定的参数

推广到 $w$ 和 $b$

二维图上：

可以发现 点击量 $y$ 的波动具有周期性，所以可以对函数进行推广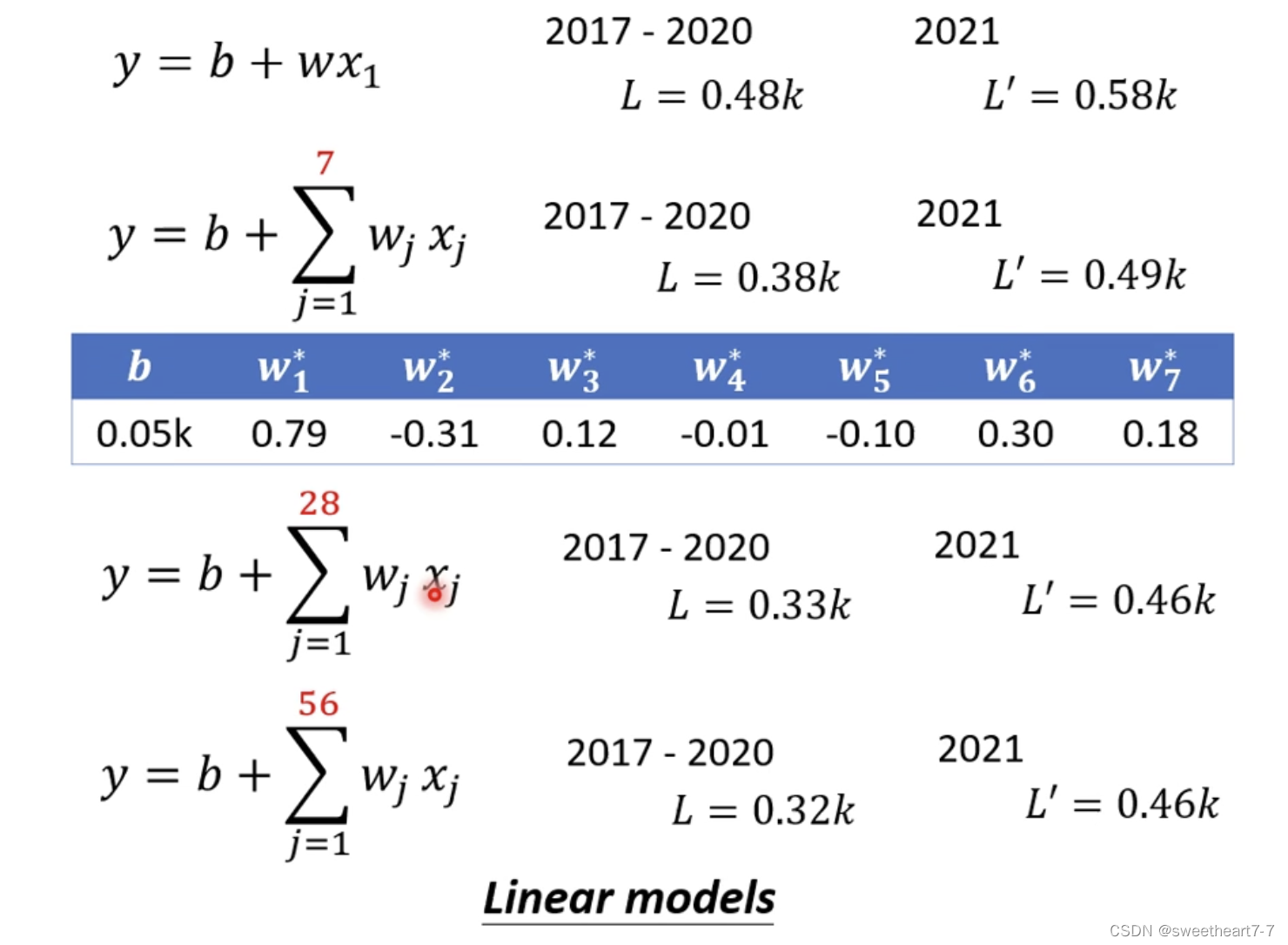

上面这些模型统称为 Linear models