【LetMeFly】952.按公因数计算最大组件大小：建图 / 并查集

力扣题目链接：https://leetcode.cn/problems/largest-component-size-by-common-factor/

给定一个由不同正整数的组成的非空数组 nums ，考虑下面的图：

• 有 nums.length 个节点，按从 nums[0] 到 nums[nums.length - 1] 标记；
• 只有当 nums[i] 和 nums[j] 共用一个大于 1 的公因数时，nums[i] 和 nums[j]之间才有一条边。

返回 图中最大连通组件的大小 。

 

示例 1：

输入：nums = [4,6,15,35]
输出：4

示例 2：

输入：nums = [20,50,9,63]
输出：2

示例 3：

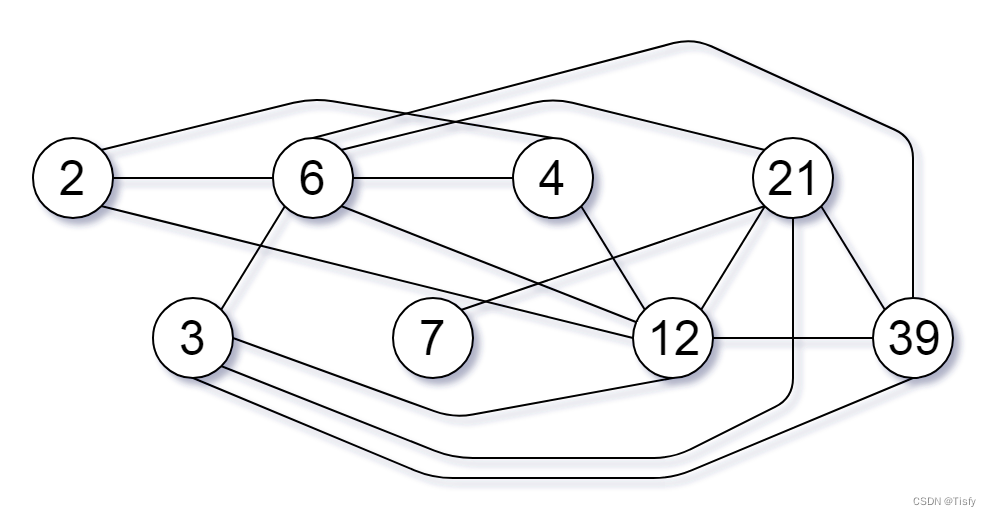
输入：nums = [2,3,6,7,4,12,21,39]
输出：8

 

提示：

• 1 <= nums.length <= 2 * 104
• 1 <= nums[i] <= 105
• nums 中所有值都 不同

方法一：建图 + 广搜

首先将数组中的每个数分解因数，用hasThisFactor[i]存放数组中有因素i的数，用num4Factor[i]存放数组中的元素i的所有的因数。

vector<vector<int>> hasThisFactor(100010);
vector<vector<int>> num4Factor(100010);
for (int t : nums) {
    int k = sqrt(t);
    for (int i = 2; i <= k; i++) {
        if (t % i == 0) {
            hasThisFactor[i].push_back(t);
            num4Factor[t].push_back(i);
            if (t / i != i) {
                hasThisFactor[t / i].push_back(t);
                num4Factor[t].push_back(t / i);
            }
        }
    }
    // 自己是自己的因数
    hasThisFactor[t].push_back(t);
    num4Factor[t].push_back(t);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

之后，遍历每一个可能的因数，并开始广搜

广搜过程中，记录每一个因数/每一个元素是否被搜索过

如果遍历到了一个未被搜索过的因数，就以此因数为起点，开始广搜建图。

拓展依据所有拥有这个因数的数($j=hasThisFactor[i]$)的所有的因数($num4Factor[j]$)

// 开始建图
int ans = 0;
vector<bool> visitedFactor(100010, false);  // 标记是否遍历过
vector<bool> visitedNum(100010, false);
for (int i = 2; i <= 100000; i++) {  // 遍历所有可能的因数
    if (hasThisFactor[i].size() && !visitedFactor[i]) {  // 有 有这个因数的元素 && 未被遍历过
        visitedFactor[i] = true;  // 那么这就遍历过了
        int thisAns = 0;  // 从这个节点开始建图，初始时图中元素个数为0
        queue<int> q;  // 广搜队列
        q.push(i);
        while (q.size()) {
            int thisFactor = q.front();  // 取出一个因数
            q.pop();
            for (int thisNum : hasThisFactor[thisFactor]) {  // 遍历所有具有这个因数的元素
                if (!visitedNum[thisNum]) {  // 一个新的未被遍历过的元素
                    visitedNum[thisNum] = true;  // 标记为遍历过
                    thisAns++;  // 图中元素个数++
                    for (int thisNewFactor : num4Factor[thisNum]) {  // 遍历这个元素的所有因数（都可以连接到一个图中）
                        if (!visitedFactor[thisNewFactor]) {  // 未被遍历过的因数
                            visitedFactor[thisNewFactor] = true;  // 标记为遍历过
                            q.push(thisNewFactor);  // 入队
                        }
                    }
                }
            }
        }
        ans = max(ans, thisAns);  // 更新答案最大值
    }
}
return ans;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

• 时间复杂度$O(N\times \sqrt{M})$，其中$N$是数组中元素的个数，$M$是数组中元素的最大值(上述算法中没有统计这$N$个元素的最大值，因此按$10^5$来处理了)。遍历过程中，每个因数/元素只会被真正地处理一次和被遍历数次
• 空间复杂度$O(N\times Q+M)$，其中$Q$是数组中元素的平均质因数的个数

AC代码

C++

class Solution {
public:
    int largestComponentSize(vector<int>& nums) {
        // 分解因数到hasThisFactor中
        vector<vector<int>> hasThisFactor(100010);
        vector<vector<int>> num4Factor(100010);
        for (int t : nums) {
            int k = sqrt(t);
            for (int i = 2; i <= k; i++) {
                if (t % i == 0) {
                    hasThisFactor[i].push_back(t);
                    num4Factor[t].push_back(i);
                    if (t / i != i) {
                        hasThisFactor[t / i].push_back(t);
                        num4Factor[t].push_back(t / i);
                    }
                }
            }
            // 自己是自己的因数
            hasThisFactor[t].push_back(t);
            num4Factor[t].push_back(t);
        }
        // 开始建图
        int ans = 0;
        vector<bool> visitedFactor(100010, false);
        vector<bool> visitedNum(100010, false);
        for (int i = 2; i <= 100000; i++) {
            if (hasThisFactor[i].size() && !visitedFactor[i]) {
                visitedFactor[i] = true;
                int thisAns = 0;
                queue<int> q;
                q.push(i);
                while (q.size()) {
                    int thisFactor = q.front();
                    q.pop();
                    for (int thisNum : hasThisFactor[thisFactor]) {
                        if (!visitedNum[thisNum]) {
                            visitedNum[thisNum] = true;
                            thisAns++;
                            for (int thisNewFactor : num4Factor[thisNum]) {
                                if (!visitedFactor[thisNewFactor]) {
                                    visitedFactor[thisNewFactor] = true;
                                    q.push(thisNewFactor);
                                }
                            }
                        }
                    }
                }
                ans = max(ans, thisAns);
            }
        }
        return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

方法二：并查集

并查集的思路较为简单，把每个数的所有因数和这个数合并到一个集合中，然后统计每个集合中有多少个元素，返回最大的元素个数即可。

这里用到了自己写的并查集类UnionFind，构造时传入最大元素个数，合并x和y时调用Union(int x, int y)函数，想得到x所在集合的根时调用find(int x)函数即可很方便地使用。

• 时间复杂度$O(N\times \sqrt{M}\times \alpha (N))$，其中$N$是数组中元素的个数，$M$是数组中元素的最大值，$\alpha (N)$是平均一次并查集操作的时间复杂度（其中$\alpha$是反阿克曼函数）。
• 空间复杂度$O(M)$

AC代码

C++

class UnionFind {
private:
    int* father;
    int* rank;
public:
    UnionFind(int n) {
        father = new int[n];
        rank = new int[n];
        memset(rank, 0, sizeof(rank));
        for (int i = 0; i < n; i++) {
            father[i] = i;
        }
    }
    
    ~UnionFind() {
        delete[] father;
        delete[] rank;
    }

    int find(int x) {
        if (father[x] != x)
            father[x] = find(father[x]);
        return father[x];
    }

    void Union(int x, int y) {
        int rootX = find(x);
        int rootY = find(y);
        if (rootX != rootY) {
            if (rank[rootX] > rank[rootY]) {
                father[rootY] = rootX;
            }
            else if (rank[rootX] < rank[rootY]) {
                father[rootX] = rootY;
            }
            else {
                father[rootY] = rootX;
                rank[rootX]++;
            }
        }
    }
};

class Solution {
public:
    int largestComponentSize(vector<int>& nums) {
        // 并查集构建
        UnionFind unionFind(*max_element(nums.begin(), nums.end()) + 1);
        for (int t : nums) {
            int k = sqrt(t);
            for (int i = 2; i <= k; i++) {
                if (t % i == 0) {
                    unionFind.Union(i, t);
                    unionFind.Union(i, t / i);
                }
            }
        }
        // 统计有几个集合、每个集合中有多少个元素
        unordered_map<int, int> times;
        for (int t : nums) {
            times[unionFind.find(t)]++;
        }
        // 统计最大值
        int ans = 0;
        for (auto[root, appendTime] : times) {
            ans = max(ans, appendTime);
        }
        return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70

同步发文于CSDN，原创不易，转载请附上原文链接哦~
Tisfy：https://letmefly.blog.csdn.net/article/details/126069985