自动驾驶中的多种卡尔曼滤波算法及推导详解，值得一读！

鉴于卡尔曼滤波算在多传感器融合系统中使用的普遍性，本文将单独就卡尔曼滤波算法及自动驾驶中常用的改进卡尔曼滤波算法进行详细介绍。

首先介绍卡尔曼滤波的基本方法，然后介绍针对非线性系统改进的扩展卡尔曼滤波，最后介绍卡尔曼滤波在自动驾驶中常用的联邦卡尔曼滤波。

1960年卡尔曼第一次发表了介绍卡尔曼滤波算法的论文，但卡尔曼滤波算法第一次实际应用则是将惯性导航器与C5A军用飞机上的机载雷达集成在一起。

卡尔曼滤波算法被称为“导航组合的驮马”，因为其已经成了现代导航系统的必要部分，特别是对于像GNSS和INS这样完全不同的系统进行组合导航的系统。

卡尔曼滤波可分为线性卡尔曼滤波、扩展卡尔曼滤波、级联式和联邦式卡尔曼滤波、无迹卡尔曼滤波等，下面将详细阐述卡尔曼滤波的原理。

1. 最小方差估计

最小方差估计是指以均方误差最小作为估计准则的估计，即满足式(1)：

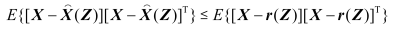
上式中，为m维系统状态变量矢量；Z为n维观测矢量；

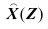
为用观测矢量Z计算得出的关于X的最小方差估计；E表示取均值，r(Z)表示由其他方法得到的X的估计值。容易证明，最小方差估计是无偏的，即残差的均值为0，满足下面式子

同样容易证明，最小方差估计的均方误差就是估计误差的方差，即

以上公式为了求得X的最小方差估计，必须首先得到X的条件概率密度，对于工程中的实际应用而言，系统状态的各种条件概率密度是很不容易得到的，因此这种估计方法的应用受到一定限制。

2、卡尔曼滤波估计

如果将估计值

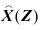
规定为观测矢量Z的线性函数，即

上式中，A和b分别是阶的矩阵和n维矢量。A值和b值仍旧按照最小方差估计来选择，则这样的估计被称为线性最小方差估计。

可以证明，这种估计只需要知道被估计值X和观测值的一、二阶统计特性，所以它比最小方差估计更加实用，尽管它的估计精度一般小于最小方差估计。

对于动态系统，工程上常常要求由t时刻的量测值Z(t)计算出该时刻状态X(t)的估计

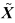
，由于X(t)是历史时刻的状态按照系统转移规律发展过来的，与历史时刻的状态有关联，所以，利用t时刻和历史时刻的所有观测值对X(t)进行估计，将有助于提高估计精度。

但是对于最小方差估计和线性最小方差估计而言，由于计算方法的限制，同时处理不同时刻的观测值而得到t时刻估计值的计算量太大。因此，这两种估计方法不适合估计动态系统的状态。

卡尔曼滤波是一种递推线性最小方差估计，它的估计准则仍是方差最小估计技术。在工程技术中，为了解工程对象(系统)的各个物理量(状态)，或者为了达到控制工程对象的目的，必须采用测量手段对系统的各个状态进行测量，由于观测值可能是系统的部分状态或其线性组合。

且包含随机误差(也称观测噪声)，最优的估计能将仅与部分相关的观测值进行处理，从而得到统计意义上估计误差最小的更多状态的估计。

因此，卡尔曼滤波是一种递推线性最小方差估计，它的估计值是观测值的线性函数，满足式(3)。并且，只要包含初始估计值在内的滤波算法初值选择正确，它的估计也是无偏的。

在计算方法上，卡尔曼滤波采用了递推模型，即在历史估计值的基础上，根据t时刻的观测值，递推得到t时刻的状态估计

。

由于历史时刻中每一时刻的估计值又是根据其历史时刻的观测值得到，所以，这种递推算法的估计值可以说是综合利用了t时刻和t时刻以前的所有观测信息得到，并且一次仅处理一个时刻的观测值，使计算量大为减少。因为卡尔曼滤波是用状态方程和观测方程来描述系统和观测值的，所以它主要适用于线性动态系统。

3、卡尔曼滤波方程

虽然工程对象一般都是连续系统，但卡尔曼滤波常常采用离散化模型来描述系统，以便计算机进行处理。离散系统就是用离散化后的差分方程来描述连续系统。

假设离散化后的系统状态方程和观测方程为：

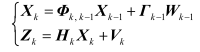
上式中，

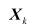
为k时刻的n维状态矢量，也是被估计矢量；为k时刻的m维观测矢量；为k-1时刻到k时刻的系统一步转移矩阵;为k-1时刻的系统噪声(r维)，为系统噪声矩阵，它表征由k-1时刻到k时刻的各个系统噪声分别影响各个状态的程度；为k时刻的观测矩阵；为k时刻的m维观测噪声。

卡尔曼滤波要求

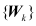
和是互不相关的零均值的高斯白噪声序列，有

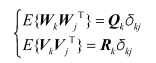
上式中，

和分别为系统噪声和观测噪声的方差矩阵，在卡尔曼滤波中要求它们分别是已知值的非负定阵和正定阵；是狄利克雷函数，即

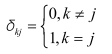
上初始状态的一、二阶统计特性为：

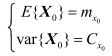
上式中，var表示求方差，卡尔曼滤波要求

和为已知量，且要求与

以及

都互不相关。

4. 离散卡尔曼滤波的计算流程

由递推的观点看，假如在k-1时刻已经获得了对

的最优估计值，并且在k时刻又观测到，则当前时刻k的最优估计值可用两者的线性组合表示，即

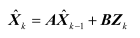
上式中，A、B待定但需保证不同维，满足

上式中，

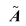
、分别为与A、B同维的任意矩阵。最终卡尔曼滤波可以按照如下流程进行计算。

状态一步预测方程为

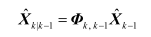
上式中状态估计计算方程为

上式中，Kk为卡尔曼滤波增益。滤波增益方程为

上式中一步预测均方误差方程为

上式中估计均方误差方程为

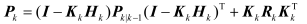
5. 扩展卡尔曼滤波

传统卡尔曼滤波要求系统的状态方程和观测方程均是线性条件，然而现实中，许多工程系统往往不能简单地用线性系统来描述，如参数估计引入增广状态方程的非线性、结构关系带来的非线性和观测信号的非线性。

因此，十分有必要对非线性滤波进行深入的讨论。一般情况是将非线性方程线性化，而后利用线性卡尔曼滤波基本方程处理线性问题。

当式(5)是非线性的，则系统状态方程和观测方程为

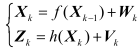
状态一步预测方程为

上式中，为过程噪声。扩展卡尔曼滤波算法就是将非线性方程线性化的滤波算法，是解决非线性滤波问题常用的一种方法。

其时间递推公式和卡尔曼滤波相似，与卡尔曼滤波算法不同的是式(11)中的状态一步预测方程中的参数要用非线性函数的一阶偏导数来计算，不具有像线性滤波那样可以实现离线计算增益和协方差的优点。

6. 联邦卡尔曼滤波

联邦卡尔曼滤波框图如图1所示。联邦卡尔曼滤波一般分为两步滤波，即先基于局部传感器进行滤波，然后再进行主滤波。先假设状态向量从k-1时刻的

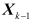
转移到k时刻的，其动力学模型为

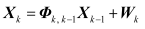
上式中

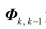
，为时间k-1到k的状态转移矩阵，为动力学模型误差，与

不相关。

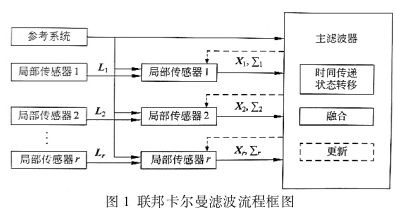
设在k时刻有r个传感器，各传感器相应的观测方程为

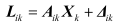
上式中，为传感器i的观测方程设计矩阵，和为传感器i的观测向量和误差向量。假设各传感器观测误差与动态模型误差不相关，各传感器观测误差互不相关。

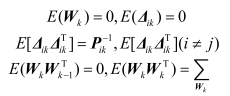
由各传感器得到局部滤波解为

上式中

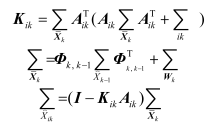
设主传感器(参考传感器)的观测向量为Lmk，则主滤波(MF)解为

上式中，Kmk和Amk分别与Kik和Aik类似。

由联邦卡尔曼滤波算法信息分享原理，可得最终融合滤波解

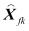
。及相应的权矩阵为

 （29）

上式中，

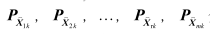
分别为局部传感器滤波输出的状态估计向量的权矩阵，为联邦滤波算法输出的状态向量的权矩阵(或称信息矩阵)，它们是相应协方差矩阵的逆矩阵。

由式(29)得

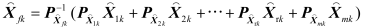
7. 总结

卡尔曼滤波算法作为一种经典算法，由于其实时性强、融合精度高，在自动驾驶领域中被广泛使用。

本文首先介绍了卡尔曼滤波的基本方法，然后介绍了针对非线性系统改进的扩展卡尔曼滤波，最后介绍了卡尔曼滤波在自动驾驶中常用的联邦卡尔曼滤波。