【算法】动态规划

1.传递信息(lcp-07-java)

小朋友 A 在和 ta 的小伙伴们玩传信息游戏，游戏规则如下：

有 n 名玩家，所有玩家编号分别为 0 ～ n-1，其中小朋友 A 的编号为 0
每个玩家都有固定的若干个可传信息的其他玩家（也可能没有）。传信息的关系是单向的（比如 A 可以向 B 传信息，但 B 不能向 A 传信息）。
每轮信息必须需要传递给另一个人，且信息可重复经过同一个人
给定总玩家数 n，以及按 [玩家编号,对应可传递玩家编号] 关系组成的二维数组 relation。返回信息从小 A (编号 0 ) 经过 k 轮传递到编号为 n-1 的小伙伴处的方案数；若不能到达，返回 0。

示例 1：

输入：n = 5, relation = [[0,2],[2,1],[3,4],[2,3],[1,4],[2,0],[0,4]], k = 3

输出：3

解释：信息从小 A 编号 0 处开始，经 3 轮传递，到达编号 4。共有 3 种方案，分别是 0->2->0->4， 0->2->1->4， 0->2->3->4。

public class LC270_lcp_07_numWays {
    public static int numWays(int n, int[][] relation, int k) {
        //已经走了i步  位置j处的方案数量
        int[][] ans = new int[k + 1][n];
        ans[0][0] = 1;
        for (int i = 1; i <= k; i++) {
            for (int[] ints : relation) {
                int a = ints[0], b = ints[1];
                ans[i][b] += ans[i - 1][a];
            }
        }
        return ans[k][n - 1];
    }

    public static void main(String[] args) {
        int i = numWays(5, new int[][]{{0, 2}, {2, 1}, {3, 4}, {2, 3}, {1, 4}, {2, 0}, {0, 4}}, 3);
        System.out.println(i);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

2.杨辉三角(118-java)

给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

示例 1:

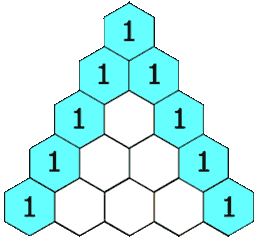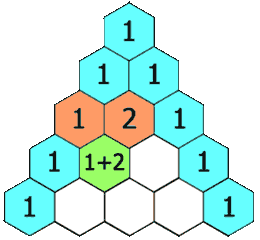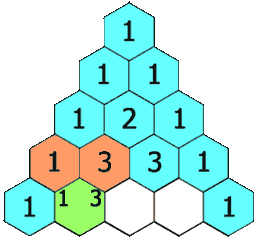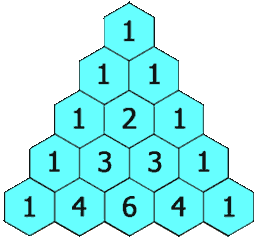
输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

public class LC82_118_generate {
    //递归
    public static List<List<Integer>> generate(int numRows) {
        List<List<Integer>> res = new ArrayList<>();
        if (numRows == 0) {
            return res;
        }
        if (numRows == 1) {
            res.add(new ArrayList<>());
            res.get(0).add(1);
            return res;
        }
        res = generate(numRows - 1);
        List<Integer> row = new ArrayList<>();
        row.add(1);
        for (int i = 1; i < numRows - 1; i++) {
            row.add(res.get(numRows - 2).get(i - 1) + res.get(numRows - 2).get(i));
        }
        row.add(1);
        res.add(row);
        return res;
    }

    //迭代
    public static List<List<Integer>> generate111(int numRows) {
        List<List<Integer>> res = new ArrayList<>();
        if (numRows == 0) {
            return res;
        }
        res.add(new ArrayList<>());
        res.get(0).add(1);
        for (int i = 2; i <= numRows; i++) {
            List<Integer> row = new ArrayList<>();
            List<Integer> pre = res.get(i - 2);
            row.add(1);
            for (int j = 1; j < i - 1; j++) {
                row.add(pre.get(j - 1) + pre.get(j));
            }
            row.add(1);
            res.add(row);
        }
        return res;
    }

    //动态规划
    public static List<List<Integer>> generate1112(int numRows) {
        List<List<Integer>> res = new ArrayList<>();
        if (numRows == 0) {
            return res;
        }
        int[][] dp = new int[numRows + 1][numRows + 1];
        dp[0][0] = 1;
        res.add(Arrays.asList(1));
        for (int i = 1; i < numRows; i++) {
            dp[i][0] = dp[i][i] = 1;
            List<Integer> row = new ArrayList<>();
            row.add(1);
            for (int j = 1; j < i; j++) {
                dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1];
                row.add(dp[i][j]);
            }
            row.add(1);
            res.add(row);
        }
        return res;
    }

    public static void main(String[] args) {
        int numRows = 5;
        List<List<Integer>> generate = generate1112(numRows);
        for (List<Integer> integers : generate) {
            for (Integer integer : integers) {
                System.out.print(integer + " ");
            }
            System.out.println();
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78

3.除数博弈(1025-java)

爱丽丝和鲍勃一起玩游戏，他们轮流行动。爱丽丝先手开局。

最初，黑板上有一个数字 N 。在每个玩家的回合，玩家需要执行以下操作：

选出任一 x，满足 0 < x < N 且 N % x == 0 。
用 N - x 替换黑板上的数字 N 。
如果玩家无法执行这些操作，就会输掉游戏。

只有在爱丽丝在游戏中取得胜利时才返回 True，否则返回 False。假设两个玩家都以最佳状态参与游戏。

示例 1：

输入：2
输出：true
解释：爱丽丝选择 1，鲍勃无法进行操作。

public class LC271_1025_divisorGame {
    public static boolean divisorGame(int n) {
        if (n == 1) {
            return false;
        }
        //桌面是i时候  做选择的是否能赢
        boolean[] ans = new boolean[n + 1];
        ans[1] = false;
        ans[2] = true;
        for (int i = 3; i <= n; i++) {
            for (int j = 1; j < n / 2; j++) {
                if (i % j == 0 && !ans[i - j]) {
                    ans[i] = true;
                    break;
                }
            }
        } return ans[n];
    }

    public static void main(String[] args) {
        boolean b = divisorGame(8);
        System.out.println(b);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

//数学逻辑
public static boolean divisorGame222(int n) {
    return (n & 1) == 0;
}
1
2
3
4

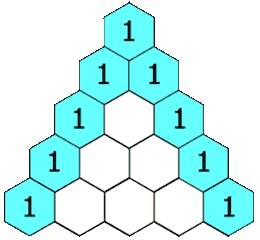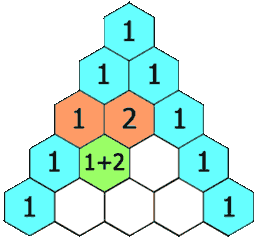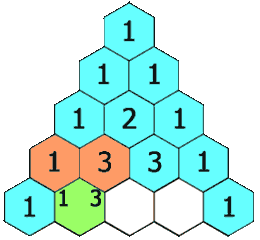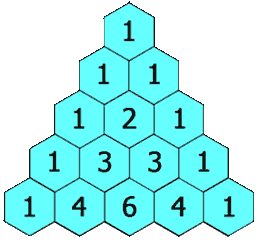
4.杨辉三角 II(119-go)

给定一个非负索引 rowIndex，返回「杨辉三角」的第 rowIndex 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

//119. 杨辉三角 II
func getRow(rowIndex int) []int {
    res := make([][]int, rowIndex+1)
    for i := 0; i <= rowIndex; i++ {
        res[i] = make([]int, i+1)
        res[i][0] = 1
        res[i][i] = 1
    }
    for i := 1; i <= rowIndex; i++ {
        for j := i; j < i; j++ {
            res[i][j] = res[i-1][j] + res[i-1][j-1]
        }
    }
    return res[rowIndex]
}

//空间复杂度优化
func getRow11(rowIndex int) []int {
    // 第rowIndex行的数组长度为rowIndex+1
    res := make([]int, rowIndex+1)
    // 每一行的第一项都确定是1
    res[0] = 1
    // 从第二行开始遍历
    for i := 1; i < rowIndex+1; i++ {
        // 第i行的首尾项确定是1
        res[0] = 1
        res[i] = 1
        // 从第i行的倒数第二个开始遍历到第二个
        for j := i - 1; j >= 1; j-- {
            // 用上一行的值求出当前res[j]
            res[j] = res[j] + res[j-1]
        }
    }
    // 返回出第rowIndex行的数组
    return res
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

5.斐波那契数(509-java)

斐波那契数，通常用 F(n) 表示，形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：

F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1
给你 n ，请计算 F(n) 。

示例 1：

输入：2
输出：1
解释：F(2) = F(1) + F(0) = 1 + 0 = 1

public class LC115_509_fib {
    //递归
    public static int fib(int n) {
        if (n == 1 || n == 2) {
            return 1;
        }
        return fib(n - 1) + fib(n - 2);
    }

    //通讯录--自顶而下
    public static int fib1111(int n) {
        if (n < 1) {
            return 0;
        }
        int[] dp = new int[n + 1];
        return help(dp, n);
    }

    private static int help(int[] dp, int n) {
        if (n == 1 || n == 2) {
            return 1;
        }
        if (dp[n] != 0) {
            return dp[n];
        }
        return help(dp, n - 1) + help(dp, n - 2);
    }

    //动态规划
    public static int fib222(int n) {
        int[] dp = new int[n + 1];
        //dp[0]默认为0
        dp[1] = dp[2] = 1;
        for (int i = 3; i <= n; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }

    //动态规划剪枝
    public static int fib2223333(int n) {
        if (n < 1) {
            return 0;
        }
        if (n == 1 || n == 2) {
            return 1;
        }
        int pre = 1;//前一项总和
        int curr = 1;//当前总和
        for (int i = 3; i <= n; i++) {
            int sum = pre + curr;
            pre = curr;
            curr = sum;
        }
        return curr;
    }

    public static void main(String[] args) {
        System.out.println(fib2223333(5));
    }
    
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62

6.第 N 个泰波那契数(1137-java)

泰波那契序列 Tn 定义如下：

T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的条件下 Tn+3 = Tn + Tn+1 + Tn+2

给你整数 n，请返回第 n 个泰波那契数 Tn 的值。

示例 1：

输入：n = 4
输出：4
解释：
T_3 = 0 + 1 + 1 = 2
T_4 = 1 + 1 + 2 = 4

public class LC190_1137_tribonacci {
    //递归--超时
    public static int tribonacci(int n) {
        if (n == 0) {
            return 0;
        }
        if (n == 1) {
            return 1;
        }
        if (n == 2) {
            return 1;
        }
        return tribonacci(n - 1) + tribonacci(n - 2) + tribonacci(n - 3);
    }

    //动态规划
    public static int tribonacci111(int n) {
        if (n == 0) {
            return 0;
        }
        if (n == 1) {
            return 1;
        }
        if (n == 2) {
            return 1;
        }
        int[] dp = new int[n + 1];
        dp[0] = 0;
        dp[1] = 1;
        dp[2] = 1;
        for (int i = 3; i < n + 1; i++) {
            dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3];
        }
        return dp[n];
    }

    public static void main(String[] args) {
        System.out.println(tribonacci(4));
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

7.使用最小花费爬楼梯(746-java)

给你一个整数数组 cost ，其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用，即可选择向上爬一个或者两个台阶。

你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。

请你计算并返回达到楼梯顶部的最低花费。

示例 1：

输入：cost = [10,15,20]
输出：15
解释：你将从下标为 1 的台阶开始。

• 支付 15 ，向上爬两个台阶，到达楼梯顶部。
  总花费为 15 。

public class LC143_746_minCostClimbingStairs {
    //动态规划
    public static int minCostClimbingStairs(int[] cost) {
        int[] dp = new int[cost.length];
        dp[0] = cost[0];
        dp[1] = cost[1];
        for (int i = 2; i < dp.length; i++) {
            dp[i] = Math.min(dp[i - 1], dp[i - 2]) + cost[i];
        }
        return Math.min(dp[cost.length - 1], dp[cost.length - 2]);
    }

    public static void main(String[] args) {
        System.out.println(minCostClimbingStairs(new int[]{1, 100, 1, 1, 1, 100, 1, 1, 100, 1}));
    }

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

8.最大子序和(53-java)

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组 是数组中的一个连续部分。

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

public class LC17_53_maxSubArray {
    /**
     * 注意判断的是sum   ans  2个变量
     *
     * @param nums
     * @return
     */
    public static int maxSubArray(int[] nums) {
        int ans = nums[0];
        int sum = 0;
        for (int num : nums) {
            if (sum >= 0) {//很关键
                sum += num;
            } else {
                sum = num;
            }
            ans = Math.max(ans, sum);
        }
        return ans;
    }

    public static void main(String[] args) {
        int[] nums = new int[]{1, 2, 3, 5, 6, 8, 9};
        System.out.println(maxSubArray(nums));
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

9.买卖股票的最佳时机(121-java)

考察:动态规划

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

示例 1：

输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

public class LC016_121_maxProfit {
    //暴力解法  超时
    public static int maxProfit(int[] prices) {
        int ans = 0;

        if (prices == null || prices.length < 2) {
            return ans;
        }
        //遍历买入点
        for (int i = 0; i < prices.length - 1; i++) {
            //遍历卖出点
            for (int j = i + 1; j < prices.length; j++) {
                ans = Math.max(ans, prices[j] - prices[i]);
            }
        }
        return ans;
    }


    //动态规划
    public static int maxProfitDP(int[] prices) {
        int len = prices.length;
        // 特殊判断
        if (len < 2) {
            return 0;
        }
        int[][] dp = new int[len][2];
        // 初始化：不持股显然为 0，持股就需要减去第 1 天（下标为 0）的股价
        dp[0][0] = 0;
        dp[0][1] = -prices[0];

        // 从第 2 天开始遍历
        for (int i = 1; i < len; i++) {
            // dp[i][0] 下标为 i 这天结束的时候，不持股，手上拥有的现金数
            //1.什么都不做,继续不持股;2.昨天持股,今天不持股
            dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
            // dp[i][1] 下标为 i 这天结束的时候，持股，手上拥有的现金数
            //1.今天什么都不做,继续持股;2.昨天之前不持股,今天持股
            dp[i][1] = Math.max(dp[i - 1][1], -prices[i]);
        }
        return dp[len - 1][0];
    }


    //空间复杂度为O(1)的解法
    public static int maxProfitDPO(int[] prices) {
        if (prices == null || prices.length < 2) {
            return 0;
        }
        int length = prices.length;
        int[] dp = new int[2];
        //第1天下标为0的时候可能持有 可能不持有
        dp[0] = 0;//不持有
        dp[1] = -prices[0];//持有
        //第二天开始遍历
        for (int i = 1; i < length; i++) {
            //分析每一天是否持有
            //dp[0] 昨天不持股,今天也不持股;    dp[1] + prices[i] 昨天持股,今天不持股
            dp[0] = Math.max(dp[0], dp[1] + prices[i]);
            //dp[1]  昨天持股,今天也持股;  -prices[i] 昨天不持股,今天持股
            dp[1] = Math.max(dp[1], -prices[i]);
        }
        return dp[0];//最后一天不持股
    }

    public static void main(String[] args) {
        int[] nums = new int[]{1, 3, 5, 6};
        System.out.println(maxProfitDP(nums));
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70