SAM

后缀自动机可以存储某一个字符串的所有子串。

一、概念

下图是一个 字符串 "aababa" 的 后缀自动机。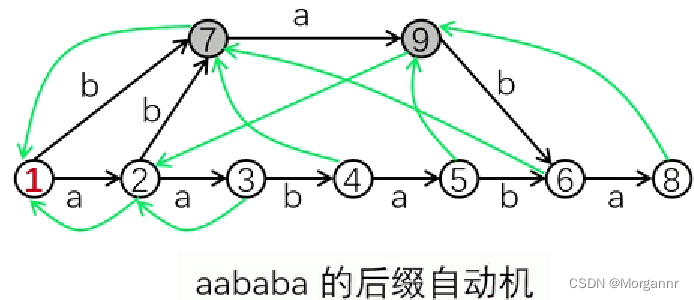

上图中的 黑色边 称 转移边，绿色边 称 链接边。

从根节点沿转移边所走的路径对应一个子串。

根节点表示空串，其他节点 表示 同类子串 的 集合。（同类子串 是指 末尾字母、结束位置相同的子串）

• 解释：上图中，绿色边与节点 构成一棵树（之后再解释），黑色边与节点 构成一张有向无环图，以 6 号点 为例，共有 3 条路径 可以 到达 6 号点，即 6 号点代表 3 个不同的子串（表示 子串的集合）
• 例如 上图中的节点代表集合：
  ② = { a } ③ = { aa } ④ = { aab } ⑤ = { aaba }
  ⑥ = { aabab，abab，bab } ⑦ = { ab，b }
  ⑧ = { aababa，ababa，baba}
  ⑨ = { aba，ba }
• 发现：同一集合 中的 所有字符串，末尾字母相同，且结束位置相同。（“同类子串集合” 含义），如对于 ⑦ 集合 来说，endpos("ab") = endpos("b") = { 3，5 }

二、构建后缀自动机

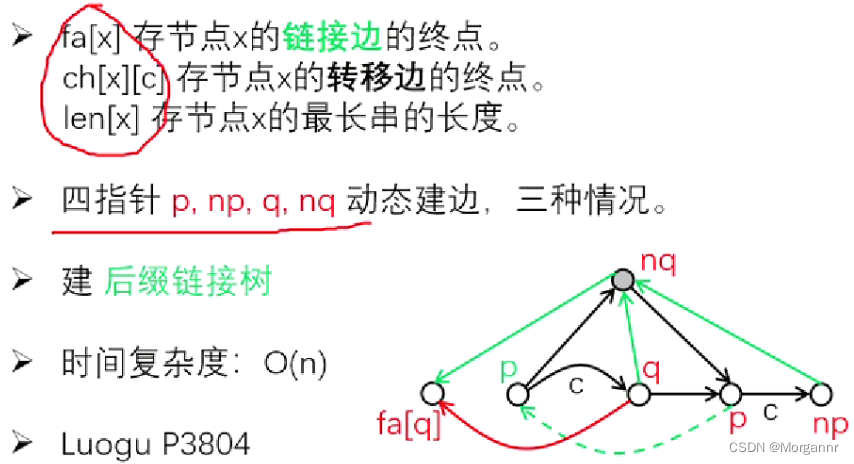
构建后缀自动机 的过程是一个 动态的过程，也就是 一个一个节点的插入，两类边（转移边，链接边）交替构建。过程中应当 维护 3 个数组：

• ch[x][c]：存 节点 x 的 转移边的终点。例：ch[1][b] = 7, ch[2][b] = 7（从上图中 ①、② 节点 沿着 b 这条边 能走到 ⑦ 这个 终点）
• fa[x]：存 节点 x 的 链接边的终点。例：fa[7] = 1，fa[6] = 7（从上图中 ⑦ 节点 沿着绿边 能走到 ① 这个 终点）
• len[x]：存 节点 x 的 最长串的长度。例：len[6] = 5，len[7] = 2（⑥ 号点所代表的字串中 最长串的长度为 5）

三、建后缀链接树

构建后缀自动机的目的 并不是在图上进行匹配，而是从图中抽离出 绿色的链接边，构建出一棵树。仔细观察上图，我们发现，每个节点有且只有一条绿色链接边指向其父节点，因此我们可以构造如下图的一棵树，我们称之为 “后缀链接树”：

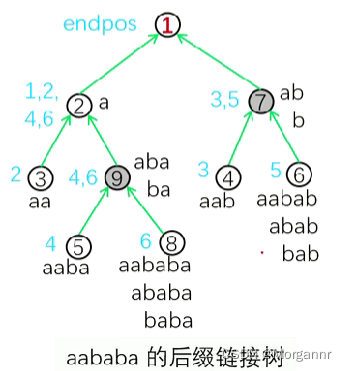
这棵树有什么 特点？

• 树上节点 表示 同类子串 及其 结束位置 的 集合。（我们将图上的信息完全转移到了这棵树上）

其 合法性：子节点 的 最短串 的 最长后缀 = 父节点 的 最长串，

• 如树中的 ⑥ 号节点 最短串为 “bab”，它 不包括自身的最长后缀是 “ab”，恰好等于 其父节点 ⑦ 号节点的 最长串 “ab”。同样，对于 ⑦ 节点，其 最短串是 “b”，它 不包括自身的最长后缀为 空，恰好等于 根节点 ① 的最长串 空。

还可以 发现，从 叶节点往上一直走到根节点 的过程中，字符串的长度 是 递减的，且除了 空 之外，字符串 末尾字母相同，

既然树上存储子串有这些 性质和规律，那我们就可以利用它们来 解决一些问题：

• 节点的子串长度：最长 len[6] = 5，最短 len[6] - len[7] = 3
  （对于 最短串长度，我们可以在 遍历的过程中，找出 当前节点 及其 父节点 最长串 长度，二者作差即为当前节点最短串长度）
• 节点的子串数量：len[6] - len[7] = 3，len[7] - len[1] = 2
  （与求当前节点最短串的长度做法一致，将当前节点及其父节点最长串长度作差即可）
• 子串的出现次数：cnt[4] = 1，cnt[6] = 1，cnt[7] = 2
  （上面画的这棵树中，节点旁边的 蓝色数字 代表着 节点代表字符串出现的位置，如 ⑥ 号节点，其代表的所有字符串都 只在 5 位置出现一次，④ 也是如此，而 ④、⑥ 节点的父节点 ⑦ 对应的 “ab”、“b” 两个串 同时 在 3、5 位置出现，也就是对应出现了 两次，而且我们发现 ⑦ 对应的次数 恰好是 其两个儿子 ④、⑥ 次数之和）

四、构建后缀自动机的具体步骤（extend 函数）

所有步骤 必须 满足上文所说的 “合法性”，这样一来才方便 抽离链接树并进行统计。

我们使用 变量 tot 为节点进行编号，根节点 为 1 号点，指针 np 总是 指向最末创建的节点，也是 从根节点开始（根节点 默认，无需创建）

int tot = 1, np = 1;
1

接下来就是 3 个数组，

//fa 链接边终点，ch 转移边终点，len 最长串长度
int fa[N], ch[N][26], len[N];
1
2

传入 extend 函数 中的 参数 是一个 偏移量 c（0 ~ 25：a ~ z，认为 传入的是一个字符）

构建的关键是 4 个指针：

• p：动态回跳指针，np：固定指向 新点指针，q：固定指向 链接点，nq：指向 新链接点。

先是 构建 “前奏”：若 ch[p][c] 不存在（p 指向的旧点 沿字符 c 没有可以走到的终点），就 从 p （旧点）向 np （新点）建 转移边。

int p = np; np = ++tot;	//p指向旧点，np是新点
len[np] = len[p] + 1; cnt[np] = 1;	//子串出现次数
//p沿链接边回跳，从旧点向新点建转移边
while (p && !ch[p][c]) {
	ch[p][c] = np;
	p = fa[p];
}
1
2
3
4
5
6
7

如果 退出 for 时 p = 0，说明 c 是个新字符，从 新点 向 根节点 建链接边

if(!p) fa[np] = 1;	//1号为根节点
1

如果 退出 for 时 p > 0，说明 ch[p][c] 存在（p 指向的旧点 沿字符 c 存在可以走到的终点），令 q = ch[p][c]

• (1) 若 p 与 q 的距离 = 1，合法，则 从 np 向 q 建链接边。
• (2) 若 p 与 q 的距离 > 1，不合法，则 裂开 q，从 np 向 nq 建链接边。

else {//如果c是旧字符
	int q = ch[p][c]; //q是链接点
	
	//2.若链接点q合法，从新点向q建链接边
	if (len[q] == len[p] + 1) fa[np] = q;
	
	//3.若链接点q不合法，则裂开q点，重建两类边
	else {
		int nq = ++tot; //nq是新链接点，是给新点找到的一个合法的父亲
		len[nq] = len[p] + 1;
		
		// 重建nq, q, np的链接边
		fa[nq] = fa[q], fa[q] = fa[np] = nq; 
		// 指向q的转移边改为指向nq
		while (p && ch[p][c] == q) {
			ch[p][c] = nq;
			p = fa[p];
		}
		//从q发出的转移边复制给nq
		memcpy(ch[nq], ch[q], sizeof ch[q]);
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

分析一下 构建过程中 变量的变化：（红色 标识 初始位置，绿色 标识 回跳后的位置）

• p：动态回跳指针，np：固定指向 新点指针，q：固定指向 链接点，nq：指向 新链接点
  
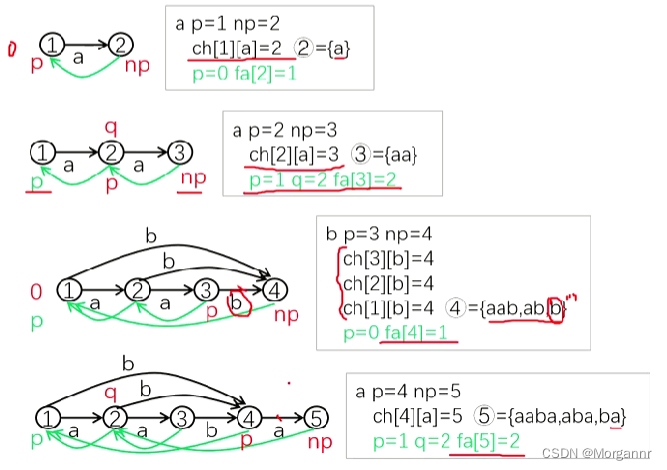
  对于上面 插入 4 个字符过程中，链接点 q 都是合法的，

而对于下方 插入第 5 个字符 b 时，p = 5，np = 6，就出现不合法的情况了，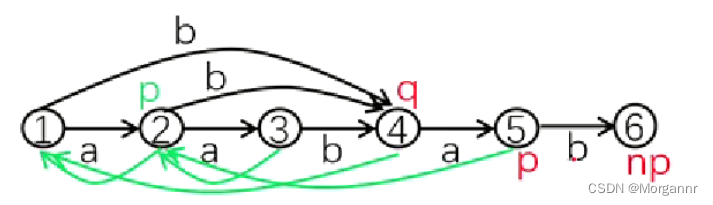
我们首先统计一下 ② ~ ⑥ 号节点所代表的字符串集合：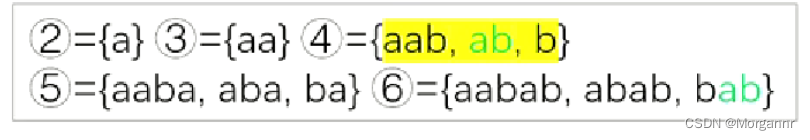
我们将目光放到 ④ 和 ⑥ 节点，对于新点 ⑥，我们应该找 其集合中的最短串的最长后缀（"ab"），显然 只有 ④ 节点包含，但是 ④ 节点 并不合法，因为 其中包含的子串 "ab" 并不是最长的，因此 不满足合法性（无法构造 后缀 链接树），

怎么办呢？这时候我们就要 将 ④ 号非法链接点裂开，

也就是从这种情况

转变为：

不难发现此时已经 增加了一个合法的链接点 ⑦，接下来就要进行一些 建边操作（共三步，可以与代码相对照理解）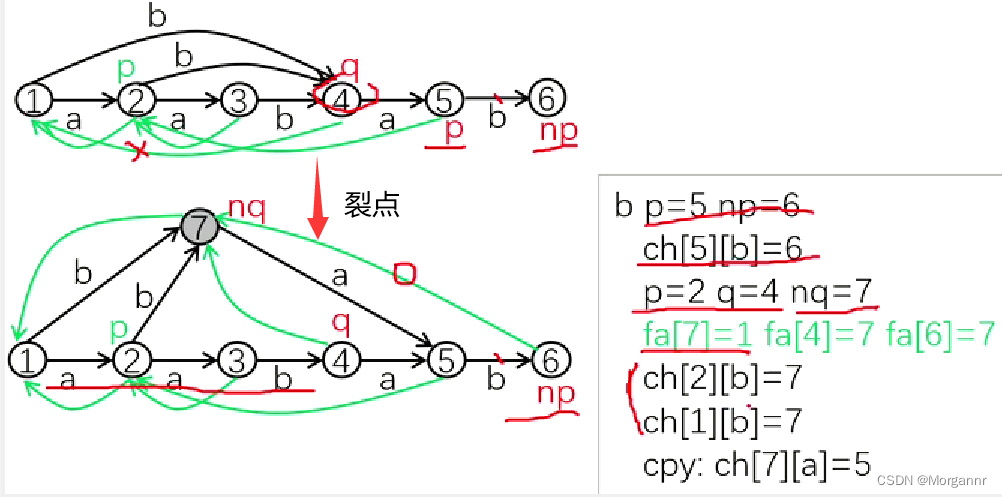

（1）更改 fa 链接边，三步走：（观察 裂点前后，两图 边的变化）

• 将 新链接点 nq = 7 指向 q = 4 的父节点：fa[7] = 1;
• 将 q = 4 节点 和 新裂开的 nq = 7 节点 链接：fa[4] = 7;
• 回到 一开始的目的，给新点找一个 合法链接点：fa[6] = 7;

// 重建nq, q, np的链接边
fa[nq] = fa[q], fa[q] = fa[np] = nq; 
1
2

（2）for 循环更改 ch 转移边：由于 ④ 号节点现在只代表 字符串 "aab" 了，因此 原来从 ② 连接到 ④ 和从 ① 连接到 ④ 的边必须要改变指向，具体指向为 新的节点 ⑦。对应上图：ch[2][b] = 7, ch[1][b] = 7;（观察 裂点前后，两图 边的变化）

// 指向q的转移边改为指向nq
while (p && ch[p][c] == q) {
		ch[p][c] = nq;
		p = fa[p];
}
1
2
3
4
5

（3）创建 从新链接点连出的转移边（有进有出），复制即可：cpy：ch[7][a] = 5;（观察 裂点前后，两图 边的变化）

//从q发出的转移边复制给nq
memcpy(ch[nq], ch[q], sizeof ch[q]);
1
2

按照下面的 模型 可以方便理解记忆代码：

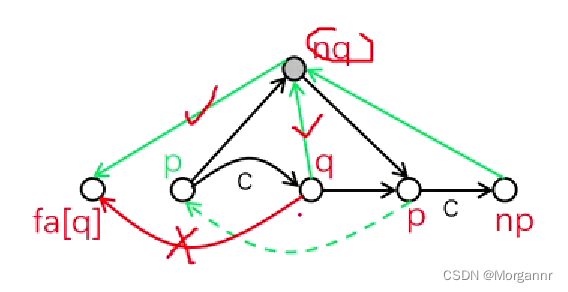
下面 不合法的过程 可在纸上模拟：

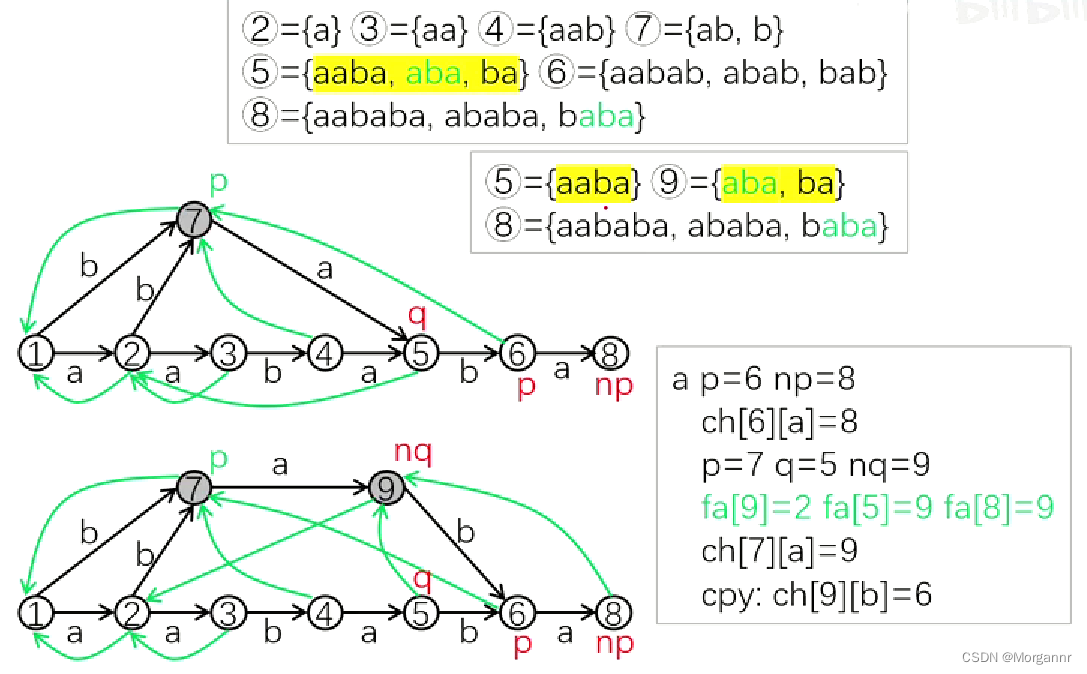
注意：

• 可以证明，长度为 n 的字符串，最多会建 2n - 1 个点和 3n - 4 条边。例如 abb…bb。

• 时间和空间复杂度都是 O(n)

• 建链接树时，点和边都开 2n 的空间

• 节点 7 和 9 是为了 满足子串集合链接的合法性 而创建的，并没影响子串的出现次数，所以 cnt[7，9] = 0

SAM 重点：

代码板子：（extend 函数）

void extend(int c) {
	int p = np;
	np = ++tot;
	len[np] = len[p] + 1, cnt[np] = 1;

	while (p && !ch[p][c]) {
		ch[p][c] = np;
		p = fa[p];
	}

	if (!p) {
		fa[np] = 1;
	}
	else {
		int q = ch[p][c];
		if (len[q] == len[p] + 1) fa[np] = q;
		else {
			int nq = ++tot;
			len[nq] = len[p] + 1;
			fa[nq] = fa[q], fa[q] = fa[np] = nq;

			while (p && ch[p][c] == q) {
				ch[p][c] = nq;
				p = fa[p];
			}
			memcpy(ch[nq], ch[q], sizeof ch[q]);
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

例题【模板】后缀自动机 (SAM)

题目描述

给定一个只包含小写字母的字符串 $S$。

请你求出 $S$ 的所有出现次数不为 $1$ 的子串的出现次数乘上该子串长度的最大值。

输入格式

一行一个仅包含小写字母的字符串 $S$。

输出格式

一个整数，为所求答案。

样例 #1

样例输入 #1

abab
1

样例输出 #1

4
1

提示

对于 $10\%$ 的数据，$|S|\le 1000$。
对于 $100\%$ 的数据，$1\le |S|\le {10}^6$。

思路：

构建后缀自动机，之后再后缀链接树上用深度优先遍历进行统计。

代码：（板子）

#include <bits/stdc++.h>

using namespace std;
//#define map unordered_map
//#define int long long
const int N = 1e6 + 10;
typedef long long ll;
char s[N];

int tot = 1, np = 1;
int fa[N << 1], ch[N << 1][26], len[N << 1];
ll cnt[N << 1], ans;
vector<int> g[N << 1];

void extend(int c) {
	int p = np;
	np = ++tot;
	len[np] = len[p] + 1, cnt[np] = 1;

	while (p && !ch[p][c]) {
		ch[p][c] = np;
		p = fa[p];
	}

	if (!p) {
		fa[np] = 1;
	}
	else {
		int q = ch[p][c];
		if (len[q] == len[p] + 1) fa[np] = q;
		else {
			int nq = ++tot;
			len[nq] = len[p] + 1;
			fa[nq] = fa[q], fa[q] = fa[np] = nq;

			while (p && ch[p][c] == q) {
				ch[p][c] = nq;
				p = fa[p];
			}
			memcpy(ch[nq], ch[q], sizeof ch[q]);
		}
	}
}

void dfs(int u) {
	for (auto v : g[u]) {
		dfs(v);
		cnt[u] += cnt[v];
	}
	if (cnt[u] > 1) ans = max(ans, cnt[u] * len[u]);
}

signed main()
{
	scanf("%s", s);
	for (int i = 0; s[i]; ++i) {
		extend(s[i] - 'a');
	}
	for (int i = 2; i <= tot; ++i) {
		g[fa[i]].push_back(i);
	}
	dfs(1);
	cout << ans << '\n';

	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66