选择多选题

• java类相关知识
• static块
• 抽象类和接口
• 面向对象特点
• 多线程ThreadLocal
• JVM常量池
• IP字段计算

唉，这些东西，背了又忘，忘了又背，背了还忘

编程题

编程题1

题解

• 直接遍历获取主对角线和副对角线元素的和
• 然后如果矩阵为奇数方阵，需要减去重复的元素

public class Solution {
        /**
         * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
         *
         *
         * @param mat int整型二维数组
         * @return int整型
         */
        public int diagonalSum (int[][] mat) {
            // write code here
            int res = 0;
            int n = mat.length;
            for (int i = 0; i < n; i++) {
                res += mat[i][i] + mat[n-1-i][i];
            }
            if (n % 2 != 0)
                res -= mat[n/2][n/2];
            return res;
        }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

编程题2

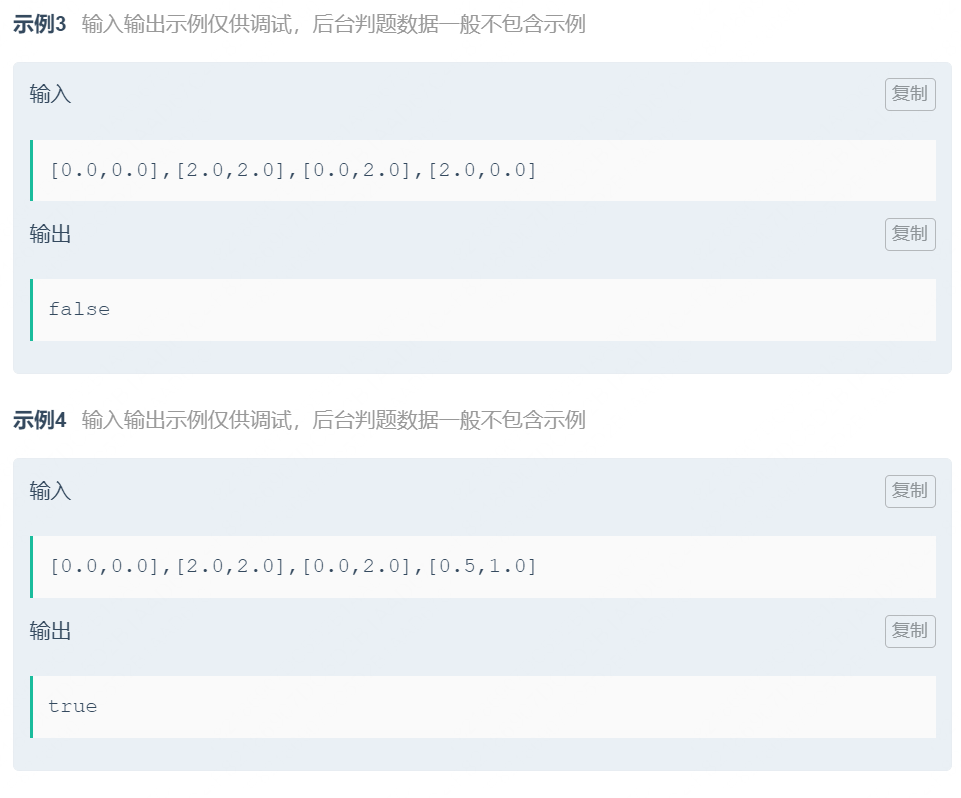
题解

这道题其实还挺常见的，特别是在游戏相关的岗位面试，结果我这菜鸡还是第一次遇到，直接蒙了…

现在下来想的话，有以下几种方法判断点是否在三角形内部：

• 三角形内角和为360度，也就是点和三角形任意两边组成一个角，这三个角的和为360度，但是浮点数计算存在无法，无法严格等于360度，该方法舍弃
• 三角形面积和，同样也是上一种方法，三角形内的点和三个顶点分别做直线，连接划分三个三角形，这三个三角形的面积和同原三角形面积相等，同样也存在浮点数计算误差的问题
• 第三种方法就是叉乘法，这一种方法比较适用，不会因为浮点数计算误差出现结果混淆的情况

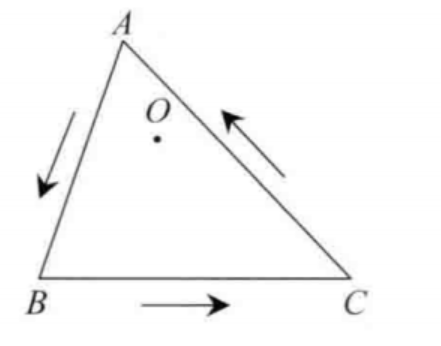
如上图所示，三角形的各个边的向量方向是逆时针方向，计算边和三角形内点o的叉乘，例如
$$\overrightarrow{CO}\times \overrightarrow{CA}$$
如果点在三角形内部，按照叉乘的计算方式，上式的结果为正数，这就是叉乘判断的原理

但是在题目中，可能存在给的三角形顶点的顺序不是逆时针的顺序，所以需要进行判断

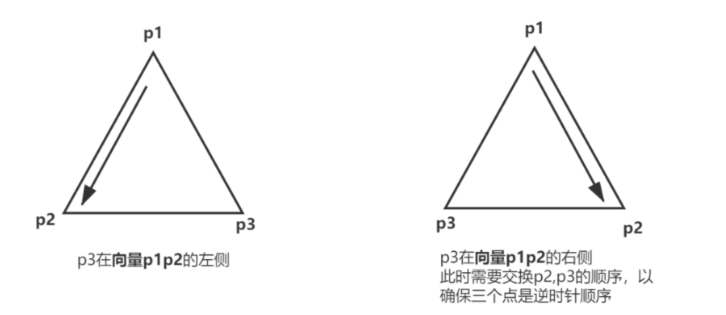
同样的也是判断叉乘公式
$$\overrightarrow{p_1{p}_2}\times \overrightarrow{p_1{p}_3}$$
如果为正数，则说明为逆时针方向，否则，调换 $p2,p3$ 的顺序

double product(double p1,double p2,double p3) {
    //首先根据坐标计算p1p2和p1p3的向量，然后再计算叉乘
    return (p2[0]-p1[0])*(p3[1]-p1[0]) - (p2[1]-p1[1])*(p3[0]-p1[0]);
}
bool isInTriangle(double p1,double p2, double p3, double o) {
    //保证p1，p2，p3是逆时针顺序
    if(product(p1, p2, p3)<0) return isInTriangle(p1,p3,p2,o);
    if(product(p1, p2, o)>0 && product(p2, p3, o)>0 && product(p3, p1, o)>0)
        return true;
    return false;
}
1
2
3
4
5
6
7
8
9
10
11

编程题3

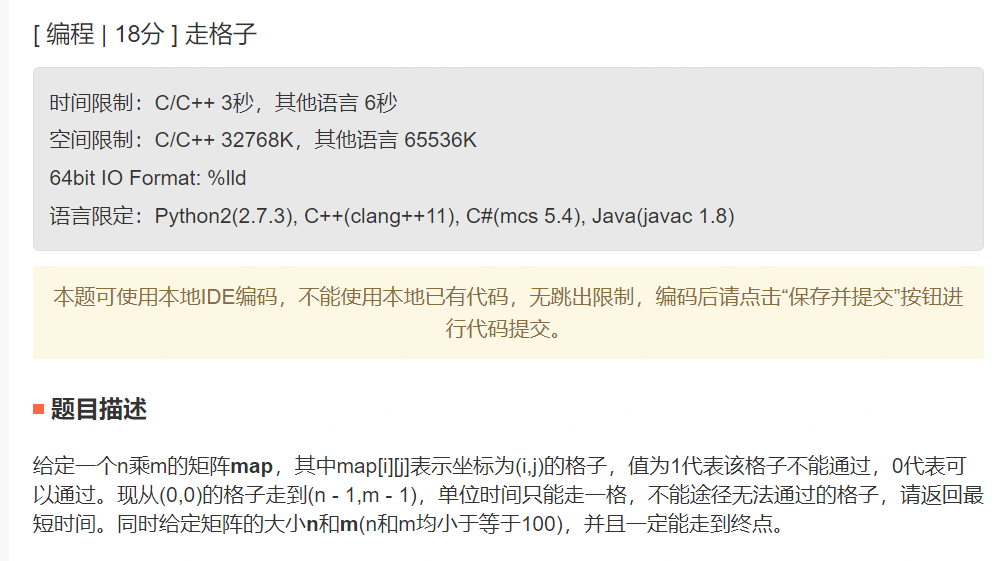
题解

这道题和 1091.二进制矩阵中的最短路径 不能说不像，只能说是一摸一样，唉，做了的题没做出来，太菜了

class Solution {
    public int shortestPathBinaryMatrix(int[][] grid) {
        int[][] dirs = new int[][]{{-1, -1}, {-1, 0}, {-1, 1}, {0, -1}, {0, 1}, {1, -1}, {1, 0}, {1, 1}};
        int n = grid.length, m = grid[0].length;
        // 起点或终点不连通，直接返回-1
        if (grid[0][0] == 1 || grid[n-1][m-1] == 1)
            return -1;
        
        boolean[][] visited = new boolean[n][m];
        Queue<int[]> queue = new LinkedList<int[]>();
        int[] start = new int[]{0, 0, 1};
        queue.add(start);
        while(!queue.isEmpty()) {
            int[] temp = queue.poll();
            for (int[] dir : dirs) {
                int x = temp[0] + dir[0];
                int y = temp[1] + dir[1];
                int weight = temp[2];
                if (temp[0] == n-1 && temp[1] == m-1)
                    return weight;
                if (x >= 0 && x < n && y >=0 && y < m && grid[x][y] == 0 && !visited[x][y]) {
                    queue.add(new int[]{x, y, temp[2] + 1});
                    visited[x][y] = true;
                }
            }
        }
        return -1;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29