-
leetcode 剑指 Offer 46. 把数字翻译成字符串
题目描述:
给定一个数字,我们按照如下规则把它翻译为字符串:0 翻译成 “a” ,1 翻译成 “b”,……,11 翻译成 “l”,……,25 翻译成 “z”。一个数字可能有多个翻译。请编程实现一个函数,用来计算一个数字有多少种不同的翻译方法。
样例:
示例 1:
输入: 12258
输出: 5
解释: 12258有5种不同的翻译,分别是"bccfi", "bwfi", "bczi", "mcfi"和"mzi"提示:
0 <= num < 2^31
解题思路:
根据题意,可按照下图的思路,总结出 “递推公式” (即转移方程)。
因此,此题可用动态规划解决,以下按照流程解题。
动态规划:
记数字 num 第 i 位数字为 xi ,数字 num 的位数为 n ;
例如: num=12258 的 n=5 , x1=1 。-
状态定义: 设动态规划列表 dp ,dp[i]代表以 xi 为结尾的数字的翻译方案数量。
-
转移方程: 若 xi 和 xi−1 组成的两位数字可以被翻译,则 dp[i]=dp[i−1]+dp[i−2];否则 dp[i]=dp[i−1]。
- 可被翻译的两位数区间:当 xi−1=0 时,组成的两位数是无法被翻译的(例如 00,01,02,⋯),因此区间为 [10,25] 。
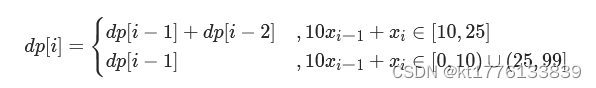
-
初始状态: dp[0]=dp[1]=1,即 “无数字” 和 “第 1 位数字” 的翻译方法数量均为 1 ;
-
返回值: dp[n] ,即此数字的翻译方案数量。
Q: 无数字情况 dp[0]=1 从何而来?
A: 当 num第 1,2 位的组成的数字 ∈[10,25] 时,显然应有 2 种翻译方法,即 dp[2]=dp[1]+dp[0]=2,而显然 dp[1]=1,因此推出 dp[0]=1。字符串遍历
- 为方便获取数字的各位 xi,考虑先将数字 num 转化为字符串 s ,通过遍历 s 实现动态规划。
- 通过字符串切片 s[i−2:i] 获取数字组合 10xi−1+xi,通过对比字符串 ASCII 码判断字符串对应的数字区间。
- 空间使用优化: 由于 dp[i] 只与 dp[i−1] 有关,因此可使用两个变量 a,b 分别记录 dp[i],dp[i−1] ,两变量交替前进即可。此方法可省去 dp 列表使用的 O(N) 的额外空间。
Java程序:
- class Solution {
- public int translateNum(int num) {
- String s = String.valueOf(num);
- int a = 1, b = 1;
- for(int i = 2; i <= s.length(); i++) {
- String tmp = s.substring(i - 2, i);
- int c = tmp.compareTo("10") >= 0 && tmp.compareTo("25") <= 0 ? a + b : a;
- b = a;
- a = c;
- }
- return a;
- }
- }
-
-
相关阅读:
Maven 插件之 docker-maven-plugin 的使用
计网学习笔记二 Link Layer Service
手机快充协议
OSI和TCP的握手/挥手
分享一个python基于数据可视化的智慧社区服务平台源码
leetcode309最佳买卖股票时机含冷冻期刷题打卡
简单shell批量文件转换gbk转为utf8编码
多线程07:async、future、packaged_task、promise
MySQL 主从复制与读写分离
API低代码开发应用场景
- 原文地址:https://blog.csdn.net/kt1776133839/article/details/126025315