lt.115. 不同的子序列

[案例需求]

[思路分析]

补充两个讲的很好的题解:

1. 点我
2. 点我

• 这道题目如果不是子序列，而是要求连续序列的，那就可以考虑用KMP。
• 这道题目相对于72. 编辑距离，简单了不少，因为本题相当于只有删除操作，不用考虑替换增加之类的。
  但相对于刚讲过的动态规划：392.判断子序列 (opens new window)就有难度了，这道题目双指针法可就做不了了，来看看动规五部曲分析如下：
  

1. 确定dp数组以及下标的含义

dp[i][j]: 以i - 1为结尾的s子序列中出现以j - 1为结尾的t的个数为dp[i][j]

2. 确定递推公式
   这一类问题, 要分两种情况;

1. s[i - 1] 与 t[j - 1] 相等
2. s[i - 1]和t[j - 1] 不相等
   
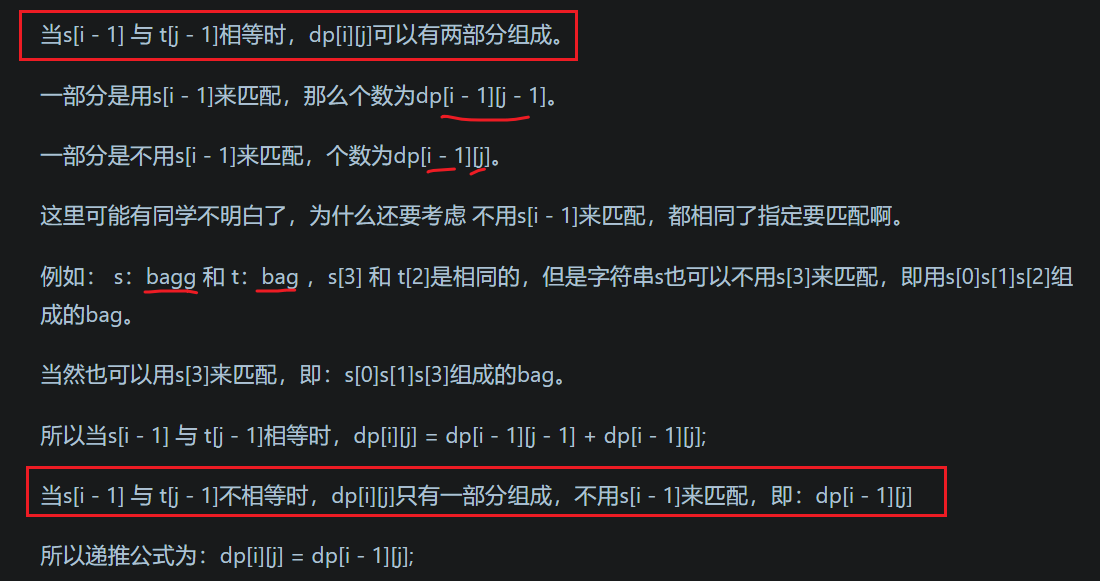
   dp[i][j] = dp[i - 1][j];

3. dp数组如何初始化
   

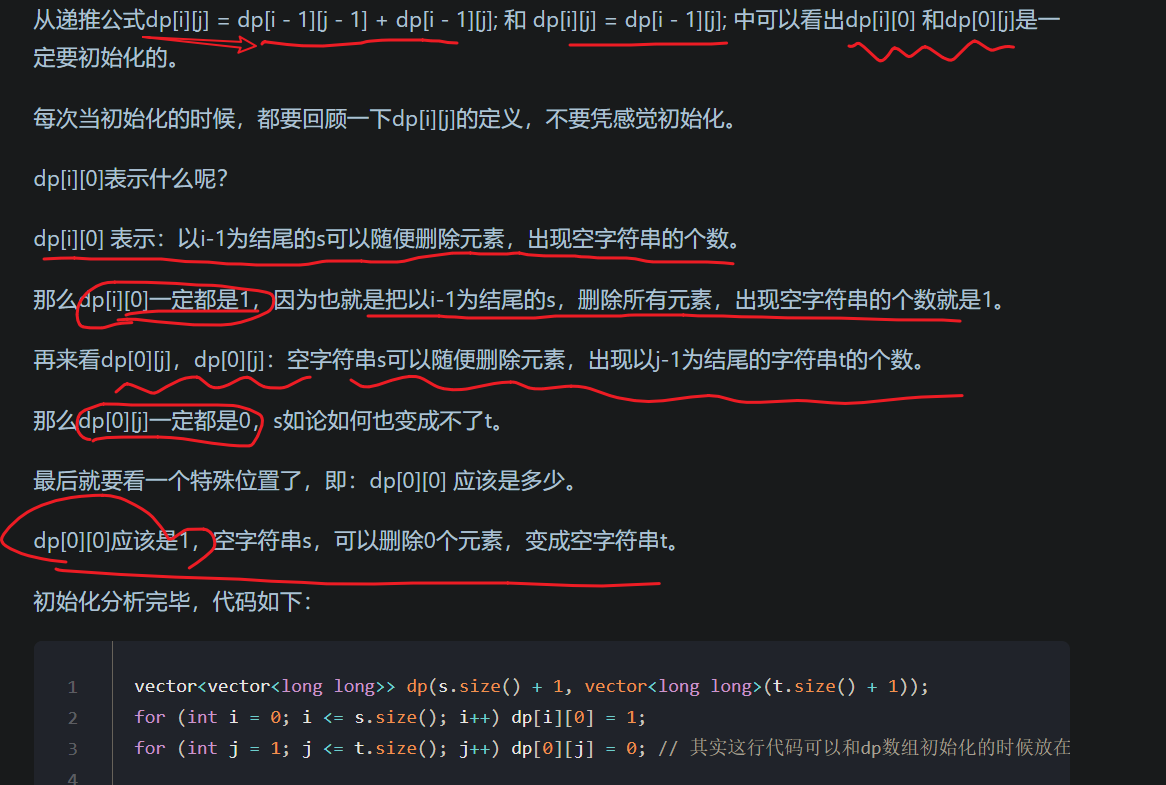
4. 确定遍历顺序
   
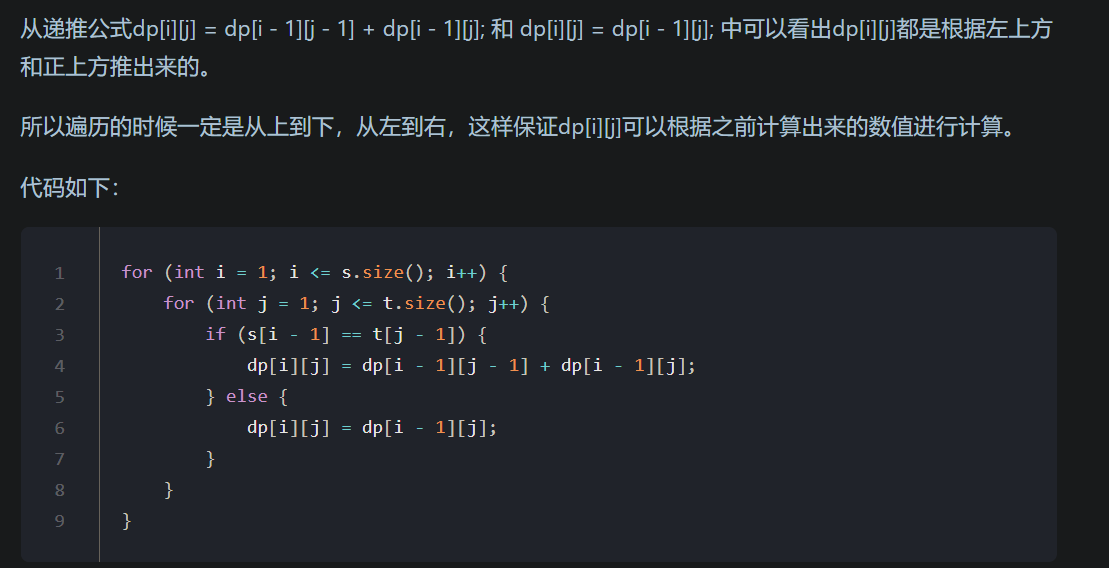
5. 举例推导dp数组
   

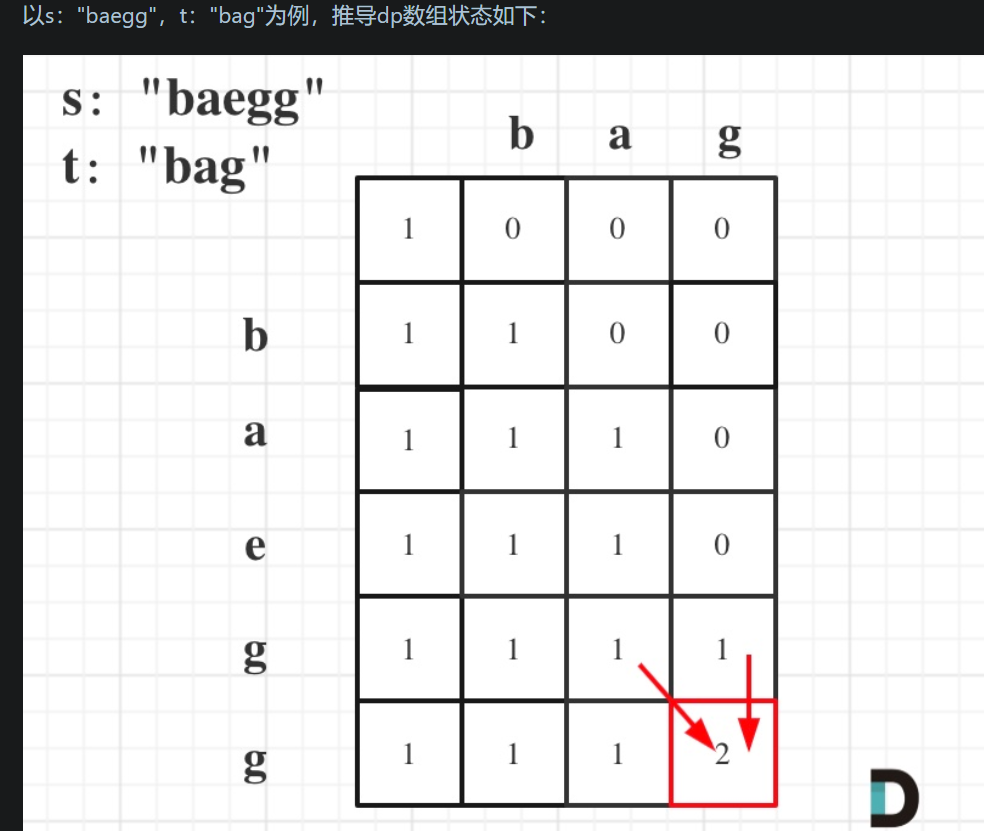
[代码实现]

class Solution {
    public int numDistinct(String s, String t) {
        //1. 确定dp数组及其含义.
        //dp[i][j] 为0~i-1字串中出现了0~j-1的字串t的个数
        int s_len = s.length();
        int t_len = t.length();
        int[][] dp = new int[s_len + 1][t_len + 1];

        //2.递推公式
        //s字串中找到能够组成t字符串的字串(不连续)
        //那么0~len -2 也就是 s[i - 1] 是否能够凑出来 t[j - 1], 也就是 j - 1长度的字串就成了切入点;
        //如果可以, s[i - 1] 能够凑出来t[j - 1], 那么dp[i][j] = dp[i - 1][j - 1]; 
        //s[i] == t[j], dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; (匹配 + 不匹配)
        //s[i] != t[j], dp[i][j] = dp[i - 1][j]; (只能不匹配,)

        //3. 初始化
        //由递推公式, i, j都是从1开始遍历的, 所以 dp[0][0], dp[i][0]都是需要初始化的.
        //dp[0][0] = 1, dp[i][0] = 1;
        for(int i = 0; i < s_len + 1; i++){
            dp[i][0] = 1;
        }
        //4. 确定遍历方式. 从左到右
        for(int i = 1; i < s_len + 1; i++){
            for(int j = 1; j < t_len + 1; j++){
                if(s.charAt(i - 1) == t.charAt(j - 1)){
//当前的s[i]和t[j]字符是匹配的,但是我们由选和不选两种情况, 都需要加上才行.
// 选的话s[i]就需要选中, t[j]也相应的匹配上了, 那么就前面的字符匹配就需要写为dp[i - 1][j - 1]
//如果不选的话,s[i]就不会被考虑. 大那是t[j]仍需要s[i]之前的元素去匹配, 就为dp[i - 1][j]
                    dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
                }else{
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        return dp[s_len][t_len];        
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

lt.583. 两个字符串的删除操作

[案例需求]

[思路分析]

待补充

[代码实现]

1