-
图的基本概念
图的基本概念
一个图 G 它可以由顶点集(图 G 中顶点的有限非空集) V 和边集(图 G 中顶点之间的关系集合) E 所组成。图中顶点个数也可以称为图的阶;任何一条边的两头必须连接某一个顶点。图不可以是空,即顶点集 V 一定是非空集,但边集 E 可以是空集。
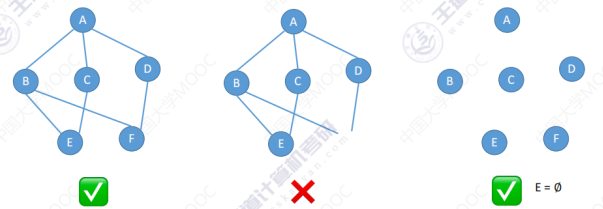
有向图 无向图 无向图里的各条边我们可以把它称为无向边(或者简称弧) 有向图里把各条边称为有向边(或者简称为边) ,v:弧尾 w:弧头 弧头弧尾顺序调换表示的不一样 (v,w) 或(w,v) 这两种方式等价 简单图:在这个图里不存在重复的边,并且也不存在顶点到自身的边。
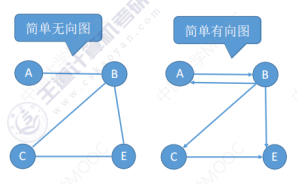
多重图
一个图里存在重复的两条边或者自身连向自身的边。
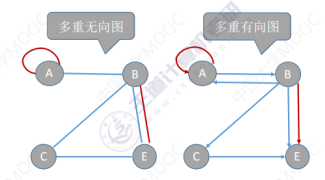
顶点的度
在无向图中,指依附于这个顶点的边到底有多少条,记为 TD(V),V指的是某一特定的点。

在有向图中,入度是以顶点为终点的有向边的数目,记为 ID(V);出度是以顶点为起点的有向边的数目,记为 OD(V);顶点 v 的度等于入度和出度之和 TD(V) = ID(V) + OD(V).

路径-----顶点 vp 到顶点 vq 之间的一条路径是指顶点序列
回路-----第一个顶点和最后一个顶点相同的路径称为回路或环
简单路径-----在路径序列中,顶点不重复出现的路径称为简单路径
简单回路-----除了第一个顶点和最后一个顶点之外,其余的顶点都不重复出现的回路
路径长度-----两个顶点之间的路径,这个路径上总共有多少条边
点到点的距离-----两个顶点之间最短路径的长度作为顶点到顶点之间的距离;如果两个顶点之间根本就不存在路径的话,那么我们需要把它们之间的距离记为∞(无穷)。
无向图中,若从顶点v到顶点w有路径存在,则称v和w是连通的;有向图中,若从顶点v到顶点w和从顶点w到顶点v之间都有路径,则称这两个顶点是强连通的.
注意:
-
对于 n 个顶点的无向图 G, 若 G 是连通图,则最少有 n -1 条边; 若 G 是非连通图,则最少有
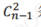 条边.
条边. -
对于 n 个顶点的有向图 G, 若 G 是强连通图,则最少有 n 条边(形成回路)
子图与生成子图
子图:一个图里边有一些顶点集和边集,取出几个顶点,然后再取出整个边集当中的某一个子集,用这样的方式构建的这个图就是原图的一个子图。注意并不是从原图当中任意选择几个顶点,任意选择几条边都能构成子图的,因为子图首先它必须是一个图。
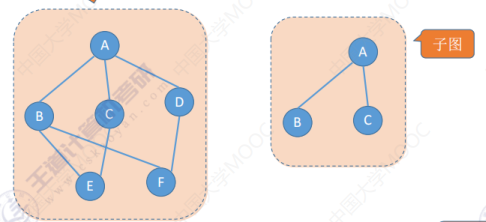
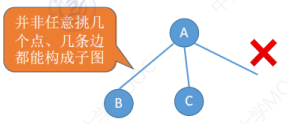
生成子图:子图里边包含了原图当中的所有顶点,那么这个子图就可以称为原图的一个生成子图。
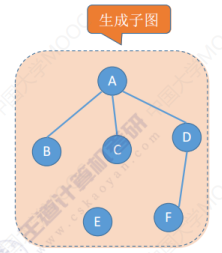
对于有向图的子图和生成图的概念一样。
连通分量(无向图)与强连通分量(有向图)
连通分量:无向图中的极大连通子图(子图必须连通,且包含尽可能多的顶点和边)
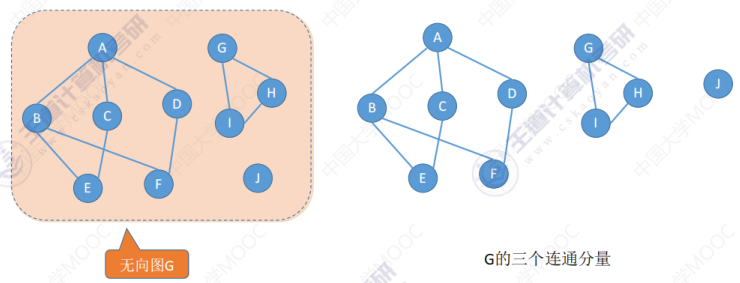
强连通分量:
如图在图 G 中A,B,E,C,D是强连通的,将这个部分择出来就是一个极大的强连通分量。而顶点 F 和 A,B,C,D,E不是强连通的(从其他顶点到 F 的路径存在,而 F 到其他顶点的路径不存在),所以 F 和 A,B,C,D,E是不强连通的。
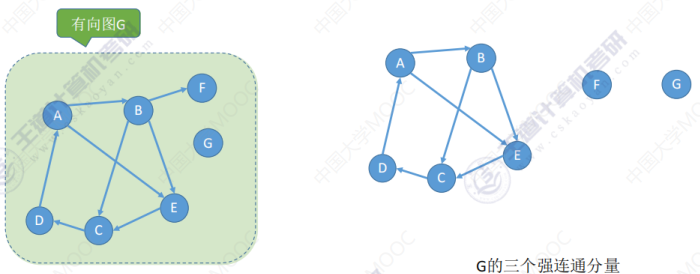
生成树和生成森林
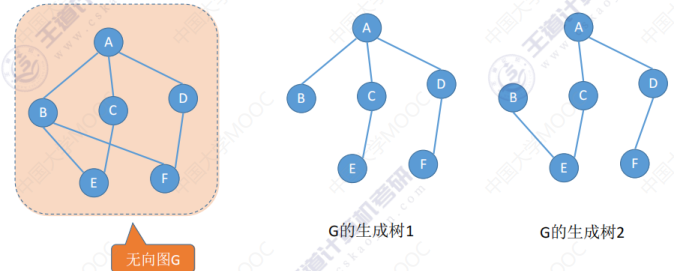
生成树:对于一个连通的无向图,它的生成树指的是这个图里边的全部顶点的一个极小的连通的子图。也就是说这个子图它要包含原图里边的全部顶点,要包含全部顶点,同时要保证这个子图连通,而且要极小(指在这个子图里边的边要尽可能的少,但要保持连通)。若图中顶点数为 n ,则他生成树含有 n-1 条边。若砍去一条边,则会变成非连通图;若加上一条边则会形成一个回路。
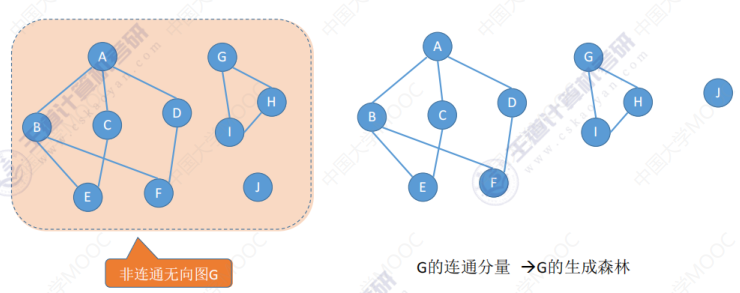
生成森林:在非连通图中,连通分量的生成树构成了非连通图的生成森林。
边的权,带权图/网,带权路径长度
边的权------为图中的每条边标上具有特殊含义的数值,这个数值则为边的权。
带权图/网------边上带有权值的图称为带权图(或网)
带权路径长度------指这条路径上所有的边的权值之和称为带权路径长度
特殊形态的图
无向完全图------其中的任何两个顶点之间都存在边
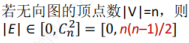
有向完全图------其中的任意两个顶点之间都存在着方向相反的两条弧
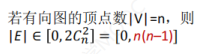
稀疏图------边很少的图稠密图------边很多的图

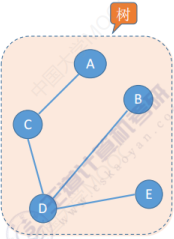
树------图里边不存在回路,并且这个图中各个节点是相互连通的,它是一个连通图。那么这种形状的图其实就是一个树对于 n 个顶点的数一定有 n 减一条边,如果说 n 个顶点的图它的边大于 n-1 条,那么这个图一定是有回路的
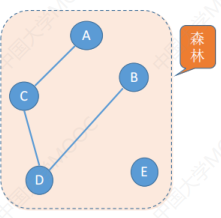
对于无向图来说,森林里边各个子图是极小的,同时各个子图又是连通的。
有向树:只有一个顶点的入度是0,然后其他所有顶点的入度都是1
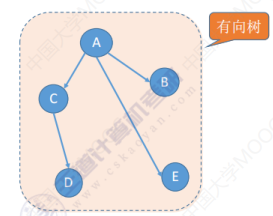
注意:树是一个连通图,各个顶点之间是连通的,但是有向树,它并不是一个强连通图。


-
-
相关阅读:
计算机毕业设计选题推荐-内蒙古旅游微信小程序/安卓APP-项目实战
AI:08-基于深度学习的车辆识别
Mybatis概述
systemverilog学习 随机化数组
SparkContext 与 SparkContext 之间的区别是什么
【ElasticSearch】深入探索 DSL 查询语法,实现对文档不同程度的检索,以及对搜索结果的排序、分页和高亮操作
T1077 统计满足条件的4位数(信息学一本通C++)
【仿牛客网笔记】项目进阶,构建安全高效的企业服务——权限控制
基于Java毕业设计音乐管理系统源码+系统+mysql+lw文档+部署软件
微信小程序---页面导航day02
- 原文地址:https://blog.csdn.net/weixin_47642634/article/details/126017876